基于SAW微力传感器的GRNN拟合研究*
季雪咪, 李媛媛, 李济同
(上海工程技术大学 电子电气工程学院,上海 201620)
0 引 言
声表面波(surface acoustic wave,SAW)技术在声学领域、电学领域和半导体学领域发展迅速[1],所制传感器能够敏感多种物理量[2],且凭借微型化、可集成度高、无源无线等优势被广泛应用[3],如SAW微力传感器。然而在测量过程中,传感器受外界环境中温度、湿度、空气等流体影响,易产生测量误差使输出数据点是离散的,难以直观体现传感器特性。以实测的离散数据点为依据预测数据值,将离散数据拟合为连续曲线[4],为后续分析传感器线性度、稳定性和准确度打下基础。因此,提高传感器输出特性曲线精确度一直是研究人员所关注的问题。
拟合传感器输入—输出特性曲线的方法通常有分段线性化法[5]、最小二乘法[6]和反向传播(back propagation,BP)神经网络[7]等。然而,分段线性化法需要分段,计算过程随着分段段数的增加而越复杂,且精确度不高;最小二乘法无法全局搜索,易求得局部最优解,且会出现病态矩阵方程失去有效性[8];BP神经网络模型构建繁琐,在学习过程中收敛速度慢,训练过程中又会陷入误差性能函数局部最小情况[9]。
针对上述传统方法的不足,本文结合SAW微力传感器,根据广义回归神经网络(general regression neural networks,GRNN)和最小二乘法基本理论,借助 MATLAB R2016b编程环境,分别对测得的数据进行曲线拟合,并分析比对拟合结果。
1 SAW微力传感器
1.1 SAW微力传感器原理
本文选取SAW微压力传感器为延迟线型结构,如图1所示。该传感器两端固定,压电基片上的两侧分别沉积输入和输出叉指换能器,外界压力施加于基片中间。基片材料具有非线性弹性行为,当外界压力F施加在压电基片上时,材料的弹性常数、密度等会因压力大小的不同而发生变化,导致SAW传播速度随之改变。与此同时,基片中间受力导致SAW传感器的结构尺寸发生改变,引起SAW波长的变化。波速和波长变化导致谐振频率的变化,通过频率与压力间关系获取传感器特性[10]。

图1 延迟线型原理
1.2 SAW微力传感器选取
压电基片材料通常使用石英、铌酸锂、钽酸锂、氧化锌等。理想情况下要求压电材料具备高机电耦合系数、低温度系数、高压电系数等[11]。综合对比可得铌酸锂的压电性能优于其他材料,因此,本文采取由铌酸锂制成的SAW微力传感器,长度L1=21 mm,宽度L2=5 mm,厚度H=1 mm,如图2所示。

图2 SAW微力传感器
1.3 数据采集
本文选取E5061A型网络分析仪对铌酸锂所制SAW微力传感器进行输出频率测量。将传感器两端引脚固定于测量铜座,铜座的两个端口通过传输线与网络分析仪连接。0~20 g的砝码表示外界微力,采用细线一端缠绕在传感器基片中间,另一端悬挂砝码,从而达到施加微力的效果。以0 g为起点,逐克递增至20 g,每增加1 g记录一次频率数据,传感器数据采集如图3所示。

图3 数据采集
在测量过程中,由于频率波动较大,需要稳定一段时间后读取数据,每克微压下记录10次频率数据,求得平均后选取20组数据,在后期数据处理时可获得对传感器输出特性更加精准的分析。SAW微力传感器输入压力和输出频率数据见表1。

表1 压力与频率数据表
2 GRNN曲线拟合
2.1 GRNN基本理论
GRNN与径向基神经网络相似,是以概率密度函数为基础的核回归方法,具有模型结构简单、人为调整参数少、收敛速度快等优势[13]。
GRNN主要目的是计算能够输出最大概率值的y。假设自变量x和因变量y,两者的联合概率密度函数用f(x,y)表示,则y的预测输出[14]为
(1)
已知训练样本数据集为{xi,yi}ni=1,应用Parzen-Rosenblatt非参数估计,密度函数f(x,y)按式(2)估算获得
(2)
式中n为训练样本容量,p为自变量x的维数,s为扩展系数,亦称为光滑因子。将式(2)代式(1)可得
(3)
2.2 GRNN仿真建立
GRNN神经网络的模型构建不复杂,需要人为调节参数少,其中包括阈值b
(4)
式中 参数s(即为扩展系数)为径向基神经网络的分布密度,从式(2)、式(3)中可以发现,当扩展系数非常大时,对实测拟合的曲线越光滑,但伴随的误差也非常大;当扩展系数非常小时,拟合曲线越逼近于实测数据,拟合精度更高,但易出现过拟合现象[15]。因此,扩展系数对GRNN的拟合精度和曲线光滑程度有着重要的影响。通过反复验证,扩展系数选取1.0。
SAW微力传感器包含2个变量,分别是最高频率与最低频率间差值Δf和所受微压力Fm。在MATLAB R2016b环境下编程,使用(f,F)表示频率和压力的函数关系。newgrnn函数是设计GRNN神经网络的核心函数
net=newgrnn(f,F,s)
在广义回归神经网络算法下的频率与压力曲线拟合效果图如图4所示。

图4 GRNN拟合效果
3 最小二乘法曲线拟合
3.1 最小二乘法基本理论
最小二乘法是一种搜索优化方法,主要目的是将拟合数据与实际测量数据间误差平方和达到最小[16]。假设给定样本数据为{(xi,yi),i=1,2,…,m},且需拟合的曲线函数为f(x,α),其中,α=(a0,a1,…,an)表示权系数。令
(5)
欲使误差平方和达到最小,对其求偏导并等于0,则
j=0,1,…,n
(6)
化解可得
(7)
α=(a0,a1,…,an)所求就是拟合曲线函数的解,此时残差平方和最小,拟合效果最佳。
3.2 最小二乘法仿真建立
给定SAW微力传感器输入压力,测得输出频率数据,则分别设为Fi和fi,i=1,2,…,n,令n=6,拟合函数为
(8)
在MATLAB R2016b环境下编程,调用Ployfit函数。
p=ployfit(f,F,6)
编程获得在最小二乘法算法下的频率与压力曲线拟合效果图如图5所示。

图5 最小二乘法拟合效果
4 GRNN和最小二乘法拟合对比


表2 三种误差统计表
由表2可以看出,GRNN的三项误差值都小于最小二乘法,最大绝对误差为-0.335 5,而最小二乘法最大绝对误差高达0.646 8。GRNN最大相对误差不超过-0.067 1,在相对应的数据点处,最小二乘法相对误差为-0.201 9。同时,GRNN的均方误差为0.017 8,最小二乘法为0.118 5,GRNN的均方误差小于最小二乘法,达1个数量级。为更直观地显示GRNN和最小二乘法的精度高低,采用折线图描述绝对误差和相对误差数据,并放入同一张图进行对比,如图6所示。
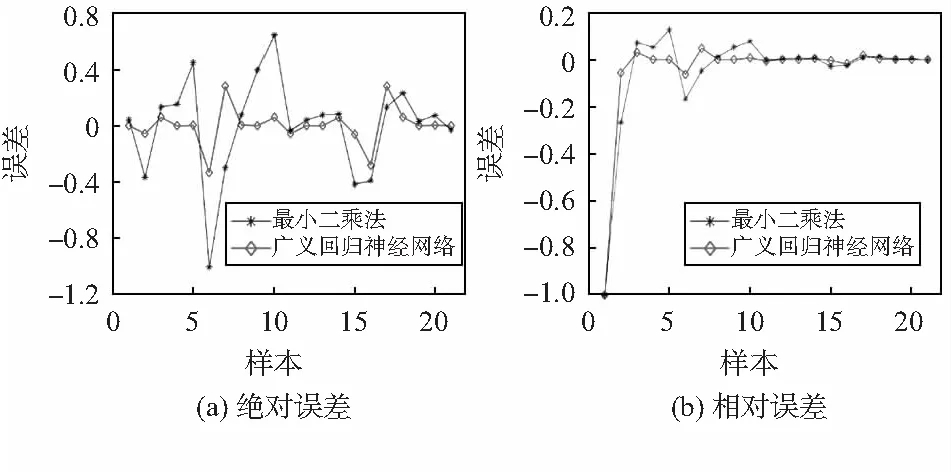
图6 两种算法的绝对误差和相对误差
由绝对误差对比图可以看出,GRNN在-0.3~0.3范围内波动,波动幅度较大的仅有4个数据点,其余数据点均逼近零。然而最小二乘法误差曲线上下波动范围大,最大高达-0.368 0。一般认为相对误差小于等于5 %满足精度要求,由相对误差对比图可以看出,GRNN相对误差在5 %范围内浮动,最小二乘法波动大,达10 %以上。由此可见,采用GRNN对器件承载的外界微力进行预测和拟合,曲线的整体误差和精确度准确度,均优于最小二乘法。
5 结 论
本文以SAW微力传感器为基础对比分析GRNN和最小二乘法的曲线拟合效果。仿真结果表明:GRNN和最小二乘法都能够在实测数据相同的情况下实现曲线拟合,而GRNN的相对误差和绝对误差明显小于最小二乘法,均方误差更是少1个数量级,拟合精度更高。其次,GRNN对于一些不稳定数据,拟合效果更佳,且模型构建简单,需自行调整参数少。由此可见,利用GRNN提高SAW微力传感器输入压力与输出频率拟合曲线精度的方式有效且可靠。

