水中丝爆等离子体破岩机理研究

马 瑞， 周世生， 胡燕川, 孙西濛， 薛启龙， 曲 骏

(1.北京市政路桥股份有限公司，北京 100045； 2.中国地质大学〈北京〉工程技术学院,北京 100083； 3.自然资源部深部地质钻探技术重点实验室， 北京 100083)

0 引言

在隧道开挖、矿山开采等基础工程建设中，岩石爆破技术发挥着重要作用。随着工程难度的增加以及对环境方面的要求，传统的炸药碎岩技术在应用中受到很大制约。机械胀裂法在遇到硬脆性岩体时施工进度会大大降低，而且机械式工具比较容易磨损，施工工人使用劳动强度大。其他碎岩技术如热力碎岩，水力碎岩，微波碎岩等，还处于实验室研究阶段，要实现工程应用尚需时日。等离子体碎岩技术[1-2]具有无污染，破碎过程中无飞石、无有害气体的产生，使用方便，作业效率高，是替代炸药碎岩的最有效可行的方法。液电等离子体理论在纳米材料制备、污水处理、石油天然气钻井，医疗碎石、液电加工成型等方面都有广泛应用。然而将其用于工程上的大型岩石破碎[3-8]，此方面的研究还较少。

高压脉冲放电时采用电爆丝引弧，水中放电是主要方式，电爆丝脉冲放电以其复杂的高能物理过程，并伴有产生的稠密等离子体、强紫外光、强氧化性自由基和强冲击波等多种效应，成为目前研究的热点[9-10]。然而对于水中丝爆的放电过程，其机理尚不是完全清楚，本文研究了水中丝爆产生等离子体继而破碎岩石的机理，分析了高电压脉冲放电过程中的铜丝融化过程，建立了铜丝在各阶段变化的电阻模型，利用MATLAB对不同阶段放电电路的电流进行了数值仿真分析，并与实验得到的电流波形进行对比。研究发现，电流波形，上升沿时间越短，脉冲放电效果越好。铜丝变化产生等离子体的过程中，等离子体通道具有一定的电阻性。实验数据结果与模型数值计算结果基本相符。

1 水中丝爆脉冲放电电路模型

为研究丝爆放电等离子体的形成机理，本文引入分段式电阻模型，数值求解放电过程中的电流变化。电路模型中，设定储能电容器最高放电电压为40 kV，放电周期为2000 μs，回路电感与电阻分别为2.1 μH和0.5 Ω。电路模型如图1所示，图中R代表铜丝的电阻，不同实验设置可以通过调整高低放电电极之间的铜丝距离，电阻值也随铜丝的尺寸发生变化。

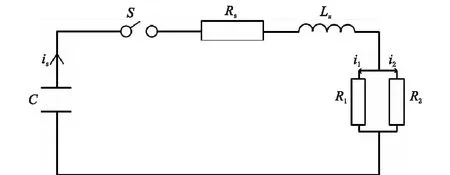
图1 水中丝爆脉冲放电电路模型Fig.1 Pulse discharge circuit model of underwater wire explosion

放电过程中电爆丝将经历5个变化阶段。

第一阶段中，电爆丝从固态升温到熔点的过程，持续时间短，电爆丝温度低，不考虑这个过程其他能量的损失，即电容器释放的能量全部转换成焦耳热作用于电阻上。

第二阶段中，即电爆丝开始发生熔解，电路中的电阻部分由固态与液态两种金属电阻组成，在电路中可以理解为两种状态的金属电阻并联在电路中，等效电路如图1所示。

第三阶段电路中电阻的形式本质上与第一阶段相似，液态电爆丝吸收热量达到沸点。

第四阶段中，电阻丝剧烈汽化产生电爆炸，该阶段等效电路类似于图1的双电阻模型，电路中电爆丝电阻存在气态电阻与液态电阻，只是该过程中气态电阻相当于无穷大。

第五阶段，是气相金属电阻与等离子体状态并存，并逐渐变为绝缘状态。即电爆丝从加热到完全断开可用3个不同的数学模型来描述，即电阻线性化模型、双电阻模型、弧道模型[1,3-4,7]。

2 水中丝爆脉冲放电过程机理分析

结合上文中的电路模型，对放电回路电爆丝在电路中的变化过程分5个过程，每个过程中放电回路分别对应相关电阻模型。通过分析各阶段电路，根据基尔霍夫定律和电阻数学模型联系建立数学方程。为便于理论计算忽略开关等电阻对电路的影响。

2.1 电爆丝固态加热段方程

电爆丝受热发生变化的第一个物理过程，金属电爆丝在电流产生的焦耳热作用下自身发生固态加热过程。CS表示电路的储能电容，lS为回路电感，RS为电路电阻。

由基尔霍夫定律和电阻模型可得如下微分方程组[22,25]：

(1)

当t=0时，表示电容放电的初始时刻，t=t1表示电路中电爆丝加热到熔点的时间点，上述方程组时间范围为0≤t≤t1，方程的初始条件(t=0)为：R1=R0(电阻丝初始时刻电阻)，i0=0，Ucs为放电电容初始放电电压值。

2.2 电爆丝液化阶段方程

第二个阶段为电爆丝的液化阶段，该过程电爆丝达到熔点，开始进行熔化过程。由于该过程的变化时间较短所以在此过程中可以看成电爆丝发生恒温熔化变化过程。模型如式(2)所示，R1和R2分别表示电爆丝的固态电阻与液态电阻，电爆丝液态电阻R2由于开始熔解时的电阻相当大，代入方程组中不易计算，所以这一阶段将电介质的电阻Ra作为液态电阻R2的初始值[2,5,8]。

根据基尔霍夫定律、节点电路方程以及与该过程建立的电阻模型可得如下微分方程组[25,27]：

(2)

该过程中的初始时刻为电爆丝加热过程完全熔解的终止时间t1、t=t2表示该过程终止时间，即电爆丝转化为液态状态。t1≤t≤t2为上述过程的时间范围。方程组的初始条件为：iS(t1+)=iS(t1-)；i1(t1+)=i1(t1-)；i2(t1)=0；R1(t1+)=R1(t1-)；R2(t1)=Ra；Ucs(t1+)=Ucs(t1-)。

2.3 电爆丝液态加热段方程

第三个阶段为电爆丝液态加热阶段，该阶段为电爆丝熔化阶段结束，液态电爆丝继续在电流的作用下持续加热，该变化过程与电爆丝变化的第一个过程相似。

根据基尔霍夫定律、节点电路方程以及与该过程建立的电阻模型可得如下微分方程组：

(3)

该过程中的初始时刻为电爆丝加热至沸点的终止时间t2、t=t3表示该过程终止时间，即电爆丝转化为液态状态。t2≤t≤t3为上述过程的时间范围。方程组的初始条件为上一过程重点附近的值：iS(t2+)=iS(t2-)；i2(t2+)=i2(t2-)=iS(t2+)；R2(t2+)=R2(t2-)=R20；Ucs(t2+)=Ucs(t2-)[22,25,27]。

2.4 电爆丝气化阶段方程

第四个阶段为电爆丝的气化过程，该阶段过程中电爆丝发生剧烈的气化现象，发生爆炸作用，开始产生高能等离子体，对电介质、岩石产生巨大的冲击力。该过程的变化原理相似于电爆丝第二个变化阶段，即液态金属R2和气态金属R3的双电阻模型，该阶段开始时由于气态电爆丝的电阻阻值相当于无穷大，但电介质的电阻作用，R3不能以无穷大代入运算，所以在这一阶段将水介质电阻Ra作为的气态电阻R3初始值进行考虑[9-10,23]。

根据基尔霍夫定律、节点电路方程以及与该过程建立的电阻模型可得如下微分方程组[25,27]：

(4)

用t4表示电爆丝完全气化的时刻，该过程的作用时间为t3≤t≤t4。该过程的初始时t=t3初始值由上一阶段终止时的值来确定。

2.5 电爆丝熄灭阶段方程

第五个阶段为电爆丝的熄灭阶段，这一过程为电爆丝金属蒸汽电阻作用，其电阻使用弧道模型表示。

根据电路等效图可以列出如下方程：

(5)

本阶段初始条件为：i3=iS；iS(t4+)=iS(t4-)；i3(t4+)=i3(t4-)；R30=R3(t4)；Ucs(t4)=Ucs(t4+)=Ucs(t4-)

针对上文推导出来的各个阶段电路元件电阻与基尔霍夫定律推导出的微分方程组，进行数值求解。用MATLAB软件进行数值模拟分析，选取合理的物理量参数，根据实验设计对放电电压、电容量、电爆丝电阻等参数的设置，可得到相应的计算结果。

3 放电回路影响因素分析

通过MATLAB对放电过程的各个阶段所建立的模型进行数值计算，针对各个放电阶段微分方程组，以各个阶段电爆丝所需的物理量为判断标准，通过电爆丝在放电过程自身温度随时间变化为判断不同阶段起始时间：

(6)

式中：Rf、C0——分别为电爆丝的电阻和比热；ρ、S、l——分别代表电爆丝的密度、横截面积和有效长度；t0——加热前电爆丝初始绝对温度[4,23]。

在模拟计算中，改变回路电阻、电感、爆丝等参数，计算分析上述参数的变化对脉冲电流的影响。模型中设定回路电阻为0.4 Ω，电介质等效电阻为0.01 Ω，回路电感为2 μH，电介质等效电阻为0.1 Ω[17,21]。

3.1 回路电感的影响

结果如图2所示，回路电感的变化对放电电流的影响，选取回路中各参数为：Ucs=20 kV，CS=1280 μF，RS=0.3 Ω，LS=0.5、5、20 μH。电爆丝尺寸为d=1.1 mm，l=30 mm。从图2可知，放电回路电感值越小，波头时间愈短，电流上升沿越陡。当回路增加一个数量级的电感，回路电流降低的较明显。回路电感对脉冲电流影响较大，故在系统装置设计与构建中尽量降低回路电感[24,26]。

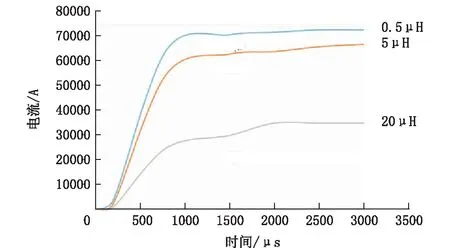
图2 回路电感对脉冲电流上升沿的影响Fig.2 Effect of the loop inductance on the rising edge of the pulse current

3.2 回路电阻的影响

如图3所示，反映了脉冲放电过程中回路电阻对电流波形的影响，脉冲放电回路中各参数同上，回路电阻RS取值分别为0.4、4、40 Ω。由图3计算结果可见，电流的峰值受回路电阻影响较明显，当电阻变化时，随着回路电阻的增加，电流发生了较大的变化，回路电阻越大对应脉冲电流的幅值越小。因此，在设备安装及设计过程中，尽量减少回路电阻。

图3 回路电阻对脉冲电流的影响Fig.3 Effect of the loop resistance on the pulse current

3.3 电爆丝物理性质的影响

电爆丝的不同物理特性也会影响电路的放电效果，其物理性质主要指材料的密度、电导率、比热等，表1列出了3种金属Cu、Fe和Al[4,16]的材料物理特性。

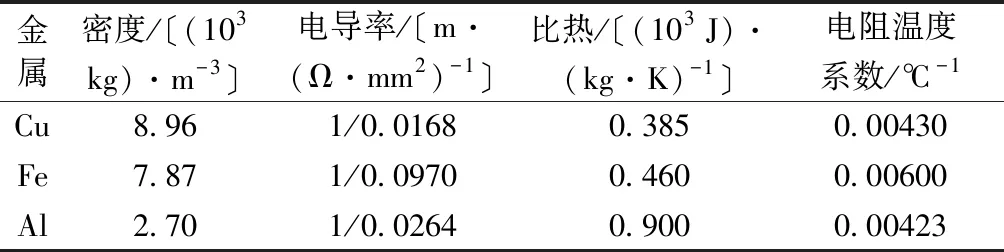
表1 电爆丝物理特性Table 1 Physical properties of the electric explosion wire

上述几种电爆丝在几何尺寸一致的情况下，对Cu、Fe和Al不同金属材质的电爆丝进行数值仿真分析，电路回路相关参数同上。如图4所示，铜丝爆时电流的幅值较大，铝和铁电爆丝脉冲电流幅值分别为铜电爆丝幅值的85%和70%。考虑成本、放电效果等因素，显然选用铜丝作为电爆丝较为合理。

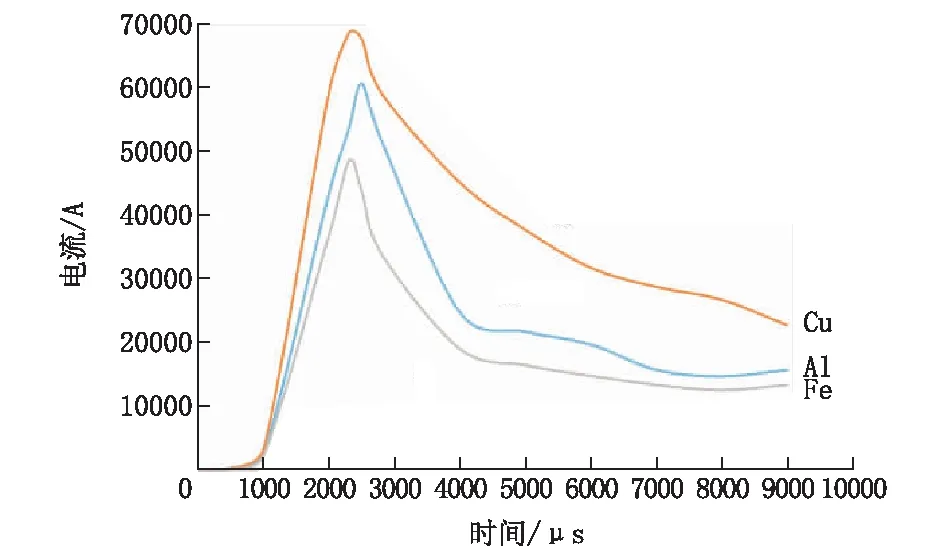
图4 电爆丝物理特性对脉冲电流的影响Fig.4 Effect of physical properties of the electric explosion wire on the pulse current

4 实验结果对比分析

在研究过程中构建了用于研究水中等离子体碎岩过程的实验系统[12,20]，该系统主要由高功率脉冲设备，等离子体电极以及电介质组成。等离子体电极连接高压脉冲放电设备的高低电极连接导线，固定好岩石与等离子体电极固定架，将实验岩块放入碎岩箱体内固定架下工字钢上，每次放电实验前在预钻孔中加入电介质，加入量至预钻孔孔口处，放入等离子体电极，固定好固定架，完成实验系统构建。采用单发脉冲放电方式，针对每种破碎实验岩石，放电实验次数会以岩石被炸开为终点(如图5所示)。记录了每次产生放电破碎的电流波形、铜丝变化情况以及岩石破碎情况。

本文研究的目的是将电爆过程中产生的较大冲击波用于岩石破碎。所以实验参数电压、电流需要较大值，才能够产生足够能量。故为验证上述放电过程机理模型的有效性，设计了4组实验，各组实验参数如表2所示。

实验过程中测量放电电路的电流变化。将实验中测得的4组实验放电电流波形图与对应的电路电流数值计算结果进行拟合比较，结果如图6所示。

图5 玄武岩和花岗岩破碎实物示意图Fig.5 Image of broken basalt and granite

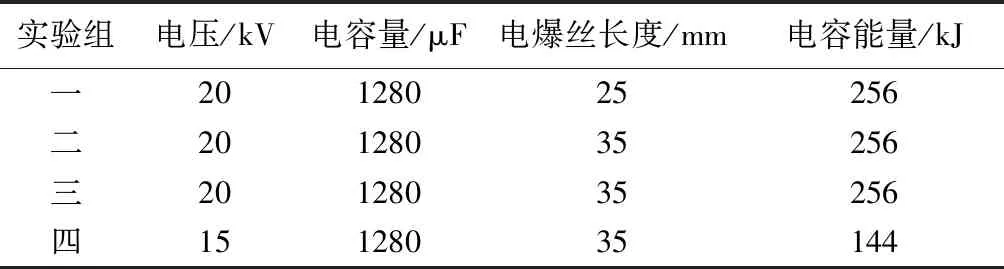
表2 实验组参数Table 2 Parameters of experimental sets

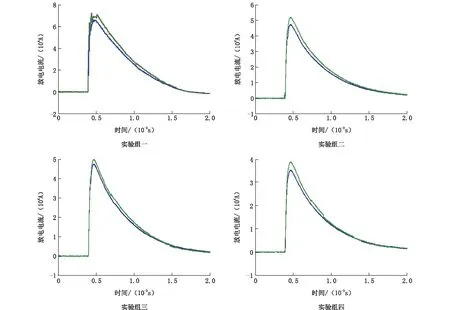
图6电流波形对比图
Fig.6Comparison of current waveforms

从4组电流波形图中可知，数值计算电路中电流与实验得到的电流波形拟合度很好，误差在10%左右，说明文中建立的电路放电机理仿真模型是合理的，可以用于工程中放电参数优化与分析。

放电过程中电爆丝的变化是多个物理过程共同作用的结果，该过程存在其他物理过程，如发光、声波等对放电电流等参数也有一定的影响，仍需进一步进行探究。在理论计算过程中参数的选取对电流理论计算影响较大，不同参数选择可能导致电路产生欠阻尼，过阻尼，临界阻尼现象，导致脉冲电流的波动较为明显。

5 总结

本文基于水中电爆丝分段电阻模型结合各阶段电路的基尔霍夫定律与节点电流公式计算出电流变化过程，对电爆丝电阻变化过程进行了数学描述。通过对比数值计算结果与实验数据，一定程度上验证了模型的正确性。

该模型考虑了电爆丝周围电介质水在放电过程中产生的电阻效应，通过多种电阻变化模型，可以验证本实验过程中电爆丝在高压脉冲作用下的变化过程以及对放电回路电流的影响；波尾后期脉冲电流的变化情况，一定程度解释了高压脉冲在空气中形成的等离子体通道是无阻态的，而在液体中放电形成的等离子体通道是具有一定阻性的。

电爆丝在放电过程中是多物理量变化的过程，该模型中忽略了等离子体作用过程中例如热动力学，光学，电磁学等物理变化过程对实验结果造成的误差影响，需要进一步深入研究该阶段发生的物理过程，完善模型。

放电回路导线、测量元件等产生的阻抗会影响由于无法准确测定所以在放电过程中实际测量电流波形与理论计算电流波形有一定的误差。储能电容器，放电线路产生的电感，放电开关电阻等电气元件在放电过程中都会产生一定的阻抗，造成理论值比实际值高。