单站定位中切向与径向运动测距模型的等价性分析
石 荣,杜 宇
(电子信息控制重点实验室,四川 成都 610036)
0 引言
对辐射源目标实施非合作的无源定位是电子侦察的重要任务之一[1-2],电子侦察站首先通过导航系统获得自身的位置坐标[3],然后对辐射源信号进行幅度、相位、频率和来波方向等参数的测量,在此基础上通过各种定位模型计算出辐射源的位置坐标,从而完成整个定位过程[4-5]。按照这一过程中参与测量的侦察站的数目又可细分为单站无源定位与多站无源定位[5-6]。单站无源定位相对于多站无源定位来讲,具有设备量小、不需要站间数据传输与时统保障、使用灵活方便等优点[7-8]。早在20世纪60~70年代的越南战争中,美军就开发了机载单站无源定位技术[9],但该技术在21世纪之后才得以迅猛发展。特别是近十多年来在此方面也发表了大量的学术论文,分别对定位过程中的参数测量[10-11]、定位方法与模型[12-13]以及误差分析等问题进行了研究,并且还有学术专著[14-15]对相关的研究成果进行了阶段性总结。回顾单站无源定位的研究历程,大家关注最多的是基于相位差变化率测量的单站定位方法,该方法主要是通过单个运动平台上装载的相位干涉仪对固定辐射源目标进行测向,同时对干涉仪中不同天线单元所接收到信号之间的相位差变化率进行测量来获得距离信息,由此给出辐射源目标的位置估计[16]。第2种单站定位方法同样是通过单个运动平台上的相位干涉仪对固定辐射源目标进行测向,然后通过不同位置处所接收到信号的多普勒频率变化率进行测量来获得距离信息,由于在给定时段内的多普勒频率变化率可由频率差来反映,所以第2种方法又可称为基于频差测量的单站定位方法。
如果从运动学的角度来看,基于相位差变化率测量的单站定位可解释为“基于切向运动测距的单站定位”;基于频差测量的单站定位可解释为基于径向运动测距的单站定位。截止到目前为止,上述2种方法都是独立研究与独立应用,给工程实现中的应用边界条件分析与性能优化带来了不便。而本文在对这2种不同模型简要回顾的基础上,利用干涉仪测向模型对相位差变化率测量与频差测量过程进行了分析,通过干涉仪不同天线单元所接收信号之间的相位差变化率测量与频差测量的固有关系,从理论上证明了单站定位中切向运动测距模型与径向运动测距模型的等价性,并通过仿真对上述理论分析结果进行了验证,从而展现了这2种单站无源定位方法的统一性。
1 单站定位的2种典型模型
运动学在高中物理与大学物理中就已经详细讲解过[17-18],大家应该都对此非常熟悉。利用运动学原理来解释运动单站对固定辐射源目标的无源定位如图1所示。
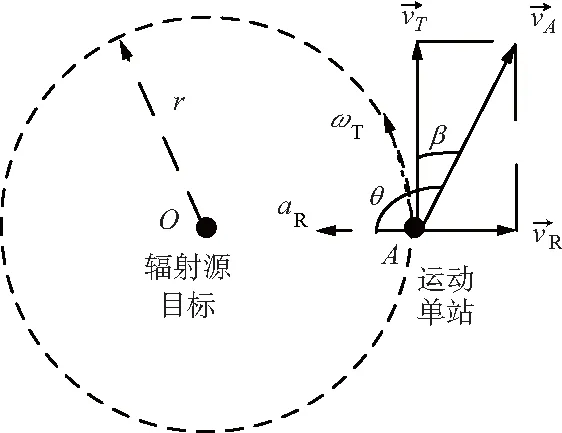
图1 运动单站定位的运动学原理解释

vT=vAcosβ=vAsinθ。
(1)
按照运动学原理,沿圆周的切向运动将引入虚拟的径向加速度,其大小记为aR,以及虚拟的角速度ωT,用“虚拟”一词是因为按照牛顿定律,加速度是由力所产生的,但在图1中做匀速直线运动的质点A没有受到任何外力,所以此处所引入的径向加速度与角速度只能看成是一个虚拟的物理量。根据运动学原理,有下式成立[17-18]:
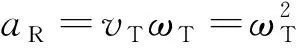
(2)
由于质点的运动速度vA是事先已知的,在运动单站完成对辐射源目标的测向之后,即可获得角度θ的测量值,并由式(1)可计算出vT。如果要完成单站定位,就需要在此基础上求解式(2)来得到距离值r。在式(2)中有2个需要进一步测量的参数,一个是角速度ωT,另一个是径向加速度aR。只要这2个参数中知道其中任意一个,即可由式(2)求解出距离值r,所以据此可划分运动单站对固定辐射源目标定位的2种典型模型。
模型1:基于切向运动测距的单站定位模型
在该模型中需要测量得到角速度ωT的值,然后由式(2)求解出距离值r如下:
(3)
“基于切向运动测距的单站定位”在工程应用中又被称为“基于相位差变化率测量的单站定位”,因为式(3)中的角速度ωT是通过运动平台上干涉仪两天线单元所接收到信号之间相位差变化率的测量来得到的。
模型2:基于径向运动测距的单站定位模型
在该模型中需要测量得到径向加速度aR的值,然后由式(2)求解出距离值r如下:
(4)
“基于径向运动测距的单站定位”在工程应用中又被称为“基于多普勒变化率测量的单站定位”或“基于高精度频差测量的单站定位”,因为式(4)中的径向加速度aR是通过对接收信号的多普勒频率变化测量或高精度频差测量来得到的[19-20]。
为了证明上述2个模型之间的等价性,需要简要阐述一下2个模型在工程实际应用中对相关物理量的测量与演算过程。
2 切向与径向运动测距的等价性
2.1 基于相位差变化率测量的单站定位

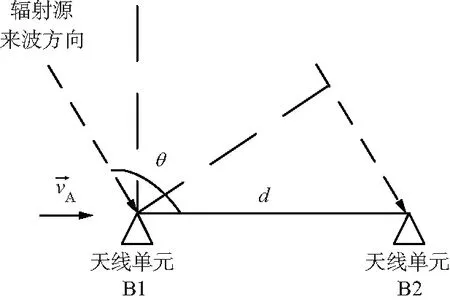
图2 运动单站平台上的干涉仪测向
设测量得到的干涉仪天线单元B1与B2所接收到辐射源信号之间的相位差记为φ,由干涉仪测向原理可得如下:

(5)


(6)
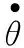
(7)

2.2 基于高精度频差测量的单站定位
如前所述,基于高精度频差测量的单站定位又称为基于多普勒变化率测量的单站定位,也就是基于径向运动测距的单站定位,需要测量径向加速度aR的值。设运动单站在极小的时间间隔ΔT内从G1点运动至G2点,在G1点处测量所接收辐射源信号的频率值为f1,在G2点处测量所接收辐射源信号的频率值为f2,如图3所示。

图3 运动单站在不同位置处对辐射源进行测量
记频率差Δf=f2-f1,在时间间隔ΔT内由径向加速度aR所产生的径向速度变化量Δv=aRΔT;根据多普勒效应原理,径向速度变化量对应了在该时间间隔内对辐射源信号的频差测量值与信号波长的乘积,即Δv=λΔf。由此便可求解出径向加速度aR如下:
(8)
于是,由式(1)、式(2)和式(8)即可求得运动单站与辐射源之间的距离r为:
(9)
式(9)中,等号右端的vA,θ,λ,ΔT,Δf在单站定位过程中都可测量,所以由式(9)即可完成距离估算。
2.3 2类模型的等价性证明
在图2中,假设干涉仪的2个天线单元B1与B2所接收到的辐射源信号的相位分别为φ1t和φ2t,此时B1与B2所测量得到的辐射源信号的频率值分别为f3和f4,如下:

(10)

(11)
于是干涉仪中2个天线单元所接收信号的频差Δf可表示为:

(12)

如果图3中频差测量的时间间隔ΔT无限缩小,那么在ΔT内单站运动的距离ΔT·vA也无限缩小。当图3中2个频差测量位置G1与G2之间的距离缩小至图2中干涉仪天线的2个天线单元B1与B2之间的距离时,于是就有ΔT·vA=d成立。在此条件下,由径向运动测距表达式(9)和式(12)可推得:
(13)
对比式(13)与式(7)可知:在单站定位中通过径向运动测距的结果与通过切向运动测距的结果二者是完全一样的;同时也说明了单站定位中切向运动测距模型与径向运动测距模型的等价性。既然二者在理论上是等价的,那么在工程应用中无论是通过何种技术途径来测量干涉仪2个天线单元所接收到信号的相位差变化率,还是测量干涉仪2个天线单元接收到信号的频率差,从效果上讲,其定位结果最终都是相同的。
另一方面,由式(12)可知,通过相位差测量,然后由相位差序列求取相位差变化率,也就自然获得了干涉仪两天线之间的频率差的测量值。这种通过测量相位差变化率来进行频差测量的方法,可由图4来进行形象的解释。

图4 干涉仪相位差变化率与频差测量图示
随着平台的运动,平台上的干涉仪在不同时刻测量出的相位差如图4中各圆点所示,由上述测量值通过最小二乘法即可拟合出一条斜线,该斜线的斜率即是干涉仪相位差变换率;根据式(12),该斜率值在除以2π之后,同时也等于干涉仪两天线之间所测量得到的目标信号频差。例如:如果测量出的相位差变化率为1°/s=0.017 5 rad/s,按照式(12)可计算出干涉仪两天线之间的频差为0.002 8 Hz。由此可见,通过图4所示的干涉仪相位差测量值的直线拟合方法,不仅能求得干涉仪2个天线单元接收到信号的相位差变化率,而且也同时得到了这2个天线单元接收到信号的高精度频差测量值。
3 仿真验证

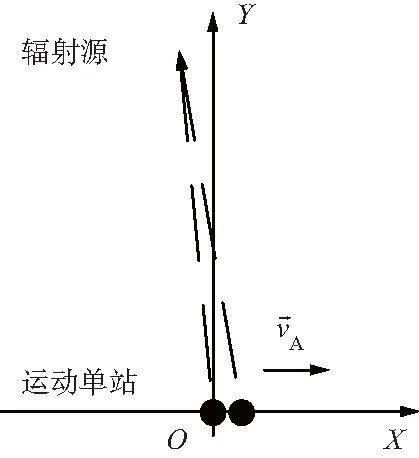
图5 运动单站定位仿真场景
在t0+1 s时刻运动单站运动到(200,0)位置处,在这1 s时间里,干涉仪进行了41次相位差测量,通道间的相位差测量误差控制5°在以内。在相位差解模糊之后的测量值与通过最小二乘直线拟合之后的数据如图6所示。

图6 干涉仪相位差测量序列与线性拟合
图6中,拟合直线的斜率为1.309 16 rad/s,于是由式(7)可计算出基于切向运动测距方法所得到的运动单站到辐射源之间的距离为159 063 m,与真实值对比误差为600 m。然后按照式(12)可求得频差测量值为0.208 4 Hz,频差测量时间间隔ΔT按0.025 s计算,由式(9)可计算出基于径向运动测距方法所得到的运动单站到辐射源之间的距离为159 063 m,这一数值与基于切向运动测距方法所得到的结果完全一致,说明了2种模型的等价性。
4 结束语
基于切向运动测距与基于径向运动测距是单站无源定位中的2种典型方法,本文通过运动平台上干涉仪中各天线单元所接收信号的相位差变化率与频差这2个物理量之间的固有关系,从理论上证明了单站无源定位中切向运动测距模型与径向运动测距模型的等价性,从而为这2种理论模型的工程应用边界条件分析提供了重要参考;另一方面,上述等价性分析也为同平台不同天线单元所接收到信号之间的高精度频差测量提供了新的途径,从理论上讲,随着测量时间的增加,频差测量精度甚至可达到0.001 Hz量级。但需要注意的是:随着时间的增加,如图4所示的相位差变化测量值所形成的线条就不再保持为一条直线,而会变成一条曲线,在此条件下可采用高次曲线拟合方法来建立更加精确的模型,求解相位差变化率的变化率(等价于求解频差的变化率)等高次项,以此来达到进一步提高定位精度目的,由于篇幅限制,该问题后续将另行撰文探讨。

