可调油膜间隙式动静压轴承参数设计
杜 雄
(上海机床厂有限公司 上海200093)
主轴的支承可选用磁悬浮轴承、陶瓷球轴承、液体滑动轴承等。磁悬浮轴承刚度低、负荷容量小、制造成本高,适用面有限,主要用于高速场合;陶瓷球轴承重量轻、热膨胀系数小、耐腐蚀,但其制造难度大、生产成本较高,主要适用于高速场合。液体滑动轴承分为静压轴承、动压轴承和动静压轴承三大类,其中动静压轴承兼有动压轴承和静压轴承的优点,能在整个运行转速范围内保持很高的油膜刚度、承载能力、主轴回转精度和抗振性,其应用更广泛。
如图1所示,可调油膜间隙式动静压轴承[1]采用内锥钢套与带有四条外锥筋的铜轴承配合形式,左右两侧布置带有内螺纹的左端盖和右端盖,当需将油膜的间隙调小时,先松开右端盖的调节螺纹,再并紧左端盖的调节螺纹,左端盖推动左挡环向右移动,迫使铜轴承压入钢套的锥孔中,当油膜间隙满足要求后,锁紧右端盖的调节螺纹。当需将油膜的间隙调大时,上述动作相反。
贵州大学的李哲[2]在2017年对可调油膜间隙式动静压轴承进行了研究,但其理论到实际应用推广还存在一定的差距。这里针对可调油膜间隙式动静压轴承结构中核心零件进行参数计算和分析,包括带锥钢套与带锥铜合金轴承之间的锥度设计、左端盖和右端盖上的调节螺纹参数设计等。
1 轴承参数确定
1.1 锥度的确定
如图2所示,间隙调小时,需对轴承施加轴向的分布力f;此时钢套与轴承之间的正压力pN,阻止轴承向右运动、由结合面产生的摩擦力为pf(大小为μpN,其中μ为钢套和轴承之间的摩擦因数)。
根据文献[3], 力平衡方程如下:
式中,α为锥度角大小。
将摩擦因数表达成摩擦角,有μ=tan φ ,则
上述pN是分布力,考虑其综合影响时按两者之间的接触面积进行计算,则有
式中,sN为钢套与轴承四条外锥筋间的接触面积。上述f也为分布力,其合力为F,则有
如图3所示,间隙调大时,需对轴承施加轴向的分布力f′,钢套与轴承之间的正压力仍记为pN;阻止轴承向左运动、由结合面产生的摩擦力为pf,其大小为μpN,力的方向与图2所示的方向相反。
此时力平衡方程如下:
同理,将摩擦因数表达成摩擦角μ=tan φ ,则有:
上述f′为分布力,其合力为F′,则有:
装配完成后,一般要求钢套和轴承之间满足自锁条件,其条件是F´≥0,即α≤φ。
根据文献[4],φ取值为0.15,则φ=arctan(0.15)=8.53°,即当α<φ=8.53°时,F´>0能实现自锁。
为使轴承自锁性可靠性高,取安全系数为2,α<φ/2=8.53°/2,即α<4.27°,此时锥度为1:6.7。同时,考虑到便于油膜间隙的调整,即轴向推力F不要过大,α不宜选择过小,最后将锥度选为1:7.5,即α=3.81°。
1.2 轴承和钢套结构尺寸
现取轴承内径d为Φ180 mm,由参考文献[5]的轴承宽径比范围L/d=(0.5~1.5),取L/d=1,故轴承宽度L=180 mm。结合锥度,参照公司同类产品设计经验,如图4所示,轴承外侧四个锥度筋的大端外径a=230 mm,小端外径b=204 mm,筋宽W=40 mm。如图5所示,钢套内孔大端内径A=230 mm,小端内径B= 206 mm,外径D取为Φ260 mm。
1.3 接触压力的确定
为了调节间隙,需要利用左端盖和右端盖的螺纹,在设计时就需要进行螺纹参数设计。这些调节螺纹,是确保两接触面产生一定的压力,使轴承产生可调节的油膜间隙量。首先要计算两锥面之间接触压力。现有的文献资料,如文献[6],只对圆柱过盈和圆锥过盈进行讨论,而这里钢套和轴承之间配合产生的过盈不属于上述两种情况。
这里假设轴承和钢套锥面的过盈仍为圆锥过盈,计算时只取轴承筋所在的圆锥部分,根据材料力学知识[7]容易知道,在连续介质效应的作用下,由圆锥过盈计算得到的接触压力很容易达到所需要的油膜间隙调节量。
由于轴承与钢套接触锥度较小,将其简化为无锥度厚壁圆筒,此时接触面的等效直径DN=(206+230)/2=218 mm,由参考文献[6],在接触压力PN的作用下,轴承的径向位移为
式中:r为轴承上任一点处半径;rd为轴承圆筒内半径,这里取Φ90 mm;rN为轴承圆筒外半径,这里取r为109 mm; E轴承为轴承材料弹性模量; υ轴承为轴承材料泊松比。
表1是本文计算所用到材料的弹性模量与泊松比。
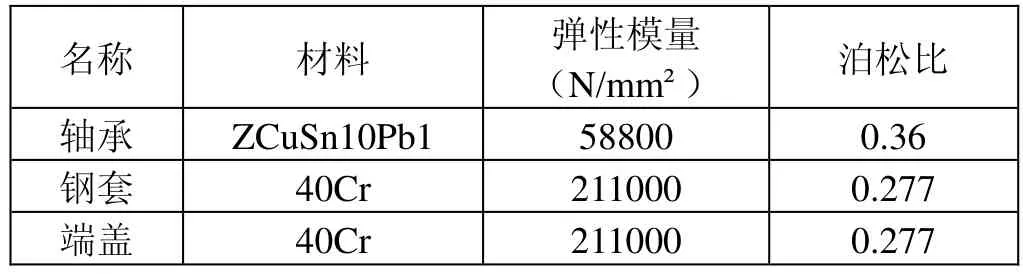
表1 动静压轴承零件材料弹性模量和泊松比
轴承内侧变形0.05 mm时,即r=rd时,u=-0.05 mm,求得压力PN=6.84 N/mm²。
轴承四条筋的面积SN=17740.92 mm² ,代入式(1)得轴承所需拉力为34482.87N。
1.4 端盖上的调节螺纹设计
如图1,拧动端盖上的调节螺纹,通过螺纹推动轴承移动,产生对轴承的拉力,由参考文献[3]知钢套的梯形螺纹中径需满足:
式中, p 为螺旋副材料的许用接触压力,MPa,对于钢和钢来说,取7.5MPa;ψ盖为结构系数,一般取1.2。
经计算,钢套上的螺纹中径参数满足要求。
调节螺纹为单线梯形螺纹,其导程为s,螺旋副材料为钢与钢,其摩擦因数取μ1=0.15,螺纹升角
由螺旋机构中梯形当量摩擦角为[3]
当β<φ1时,才能满足自锁条件,φ1/β值越大,安全性越好,由于轴承存在径向振动,令比值大于10,即取β<52.9´,s<9.65 mm。这里取梯形调节螺纹转动1/8圈就可满足轴承油膜间隙的调整量为0.05 mm,由筋的锥度为1:7.5,则导程s=8×0.05×7.5=3 mm就能满足使用要求,因此将导程定为s=3 mm。
式中:d为螺纹公称直径;b为螺纹牙根部宽度,标准梯形螺纹b=0.65s;h为螺纹牙工作高度,h=0.5s;z为承受压力的圈数,这里取20/3; σb为材料的许用应力,这里取360 MPa。
代入相关数据得导程s≥0.07 mm,前述导程数值满足强度要求。
2 有限元分析
由于前面理论计算简化了很多影响因素,实际轴向的调整力F比34482.87 N要小很多,这里利用有限元分析进行讨论和修正。
首先针对轴承进行油膜间隙调整量进行分析,即在下述外加载荷下进行静力学分析:
(1)轴承筋外锥面受垂直均布的压力作用,施加压力载荷6.84 MPa。
(2)轴承带筋的大端面施加轴向位移为0的约束。
如图6所示,红色部分A处表示轴承筋所在外锥面受垂直且均匀分布的压力作用,大小为6.84 MPa,左端端面黄色部分B处表示轴承带筋大端面施加位移固定约束,即轴向位移为0。
对模型进行自动网格划分,得到3313个节点、510个单元,求解轴承形变,得到变形如图7所示,轴承变形最大处为轴承内侧,对比前面的计算,前文要求轴承内侧发生0.05mm的变形,而本次求解施加相同力时轴承内侧产生了0.33mm变形,有较大差别。这是因为图6所示的轴承模型与厚壁圆筒的模型有一定的差距,前文计算的压力只确定施加压力的数量级大小,因此需对计算公式(2)进行修正。
这里在公式(2)中引入系数K1,形成下面的公式:
式中,K1=0.33/0.05=6.6。
由于实际轴承结构中的钢套是镶嵌在体壳内的,图6和图7计算采用的厚壁圆筒模型还是存在欠缺,这里再将Solidworks中建立的轴承和钢套三维装配体模型导入ANSYS workbench中,如图8所示,材料设置如表1所示,钢套和轴承之间的接触摩擦因数设置为0.15,对轴承装配体施加的载荷和约束要求如下:
(1)钢套大端面施加拉力为4000N,也是轴承带筋大端施加的压力F;
(2)轴承带筋大端仍不能发生轴向移动,将其轴向位移约束为0;
(3)钢套外表面与体壳接触不能产生径向位移,即径向位移约束为0。
对模型进行自动网格划分,得到40 073个节点、22 198个单元,求解装配体形变,得到变形如图9所示。
如图9所示,轴承内孔向内缩小了0.025mm,即油膜间隙变化了0.05mm,这比34482.87 N要小很多。考虑结构的影响,这里再引入一个系数 ,使式(1)的计算公式更适用,则轴承所需轴向拉力
式中,K2=0.766 ,K=0.12 。
通过圆锥过盈假设计算和对轴承和轴套装配体进行有限元分析,通过两者之间油膜间隙的变化值在圆锥过盈假设计算公式(3)中引入系数,为调节螺母其他参数计算给出了依据。
3 结语
动静压轴承由于承载能力强、旋转精度高、抗振性好等优点受到国内外厂商的青睐,本文对可调油膜间隙式动静压轴承进行了参数设计,主要结论如下:
(1)根据斜面机构的自锁原理,确定了带锥钢套和带筋铜轴承之间的接触锥度,根据公司设计经验,给出了轴承内径为180mm的轴承和钢套的结构尺寸。
(2)建立了油膜间隙变化量与轴向推力大小之间的计算模型,初步计算了一定油膜间隙调节量下的轴向力,并根据调节需要确定了调节螺纹的导程。
(3)通过有限元分析对油膜间隙变化量与轴向推力大小之间的关系模型进行了修正,使计算公式具有通用性。

