管道天然气多组分浓度在线监测方法

敖家佩,邱海峰,贾唐浩,李昕,刘卫华,雷绍充

(1.西安交通大学电子与信息学部,710049,西安;2.中国石化西北油田分公司,830000,乌鲁木齐)

随着西气东输工程投入运营,国内天然气行业进入了高速发展阶段。对管道内天然气成分和浓度进行定性与定量分析能为及时改进产品质量提供保证。所以,生产单位急需在线监测设备,从而能够时刻监测到管内气体状态,观察气体开采的过程是否正常,开采气质量是否合格。由于气体计量参数多,管道距离长,采集管道内部压力较大,情况复杂,若按传统的设备维护工作方式,设备维护人员必须到达现场,并对设备进行深度诊断维护,这个过程本身具有一定的危险性,而且工作量大,很难保证维护的及时性,易造成测量结果与实际产生偏差,引发纠纷甚至安全事故。实施对计量设备状态参数的实时监测,不仅可提高计量设备的管理效率,而且可最大限度地减少安全隐患与经济损失[1]。

天然气主要成分为烷烃,同时掺杂着许多其他气体成分,在对其种类和浓度进行监测的过程中不可避免地存在交叉敏感的问题,从而造成计量结构产生较大误差,故研究工作可从混合气体种类和浓度辨识2个层次上进行。目前最常用的辨识方法是气相色谱法,采用实时色谱仪实时取样分析,得到天然气组成,并可以在此基础上获得密度、发热量等物性参数,通过计算机进行数据实时记录,确保天然气流量计量准确可靠,保证后续气体的正常使用[2-3]。气相色谱法的最大缺陷在于数据获得周期长,需要消耗大量载气,无法真正首先和实时监测。对此,本文提出采用红外气体传感器阵列结合信息融合技术辅助,实现天然气中混合气体组分的种类识别和浓度监测。首先利用开源的样本量较大的UCI(University of California Irvine)数据库进行6种单一组分气体种类辨识继而进行浓度回归预测,根据准确度优选最佳算法方案,并将其用于实验室模拟烷烃中的气态组分甲烷、乙烷、丙烷以及用于增加压力而注入的氮气的小样本混合气体浓度预测,希望能够通过借助算法的手段,对气体浓度的偏差进行修正,结合红外传感阵列与可编程逻辑器件,实现真正的天然气气体浓度在线监测[4-5]。

1 各种算法比较与筛选

测试使用的UCI数据库是加州大学欧文分校的机器学习数据库。本文使用的数据集是其中关于数据回归类的1个,包含13 910个数据样本,由16个传感器对6种纯净单一组分在不同浓度下测得。每个传感器均记录8个特征值,对应每个样本的128个特征参数[6]。

分别采用最近邻(KNN)算法、分类回归树(CART)算法以及多层感知机(MLP)算法对6种气体的类别进行了辨识,然后,分别将3种算法的预测结果进行了比较。该数据集中所测量的6种组分依次为氨气、乙醛、丙酮、乙烯、乙醇和甲苯,所测得的浓度范围如表1所示。

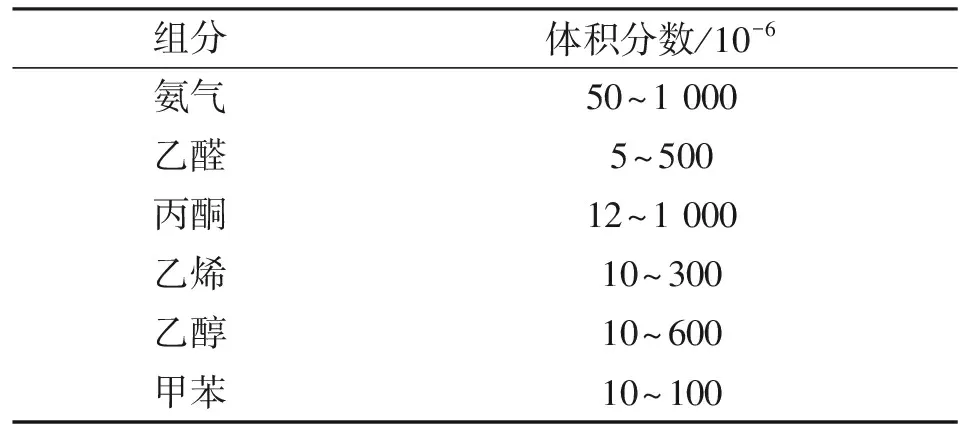
表1 气体种类及浓度范围

具体的研究步骤如下:首先,使用主成分分析(PCA)法将数据特征降维,提取其主要特征,然后采用分类算法对6种组分进行分类,以分类结果准确率为指标判断算法的优劣。

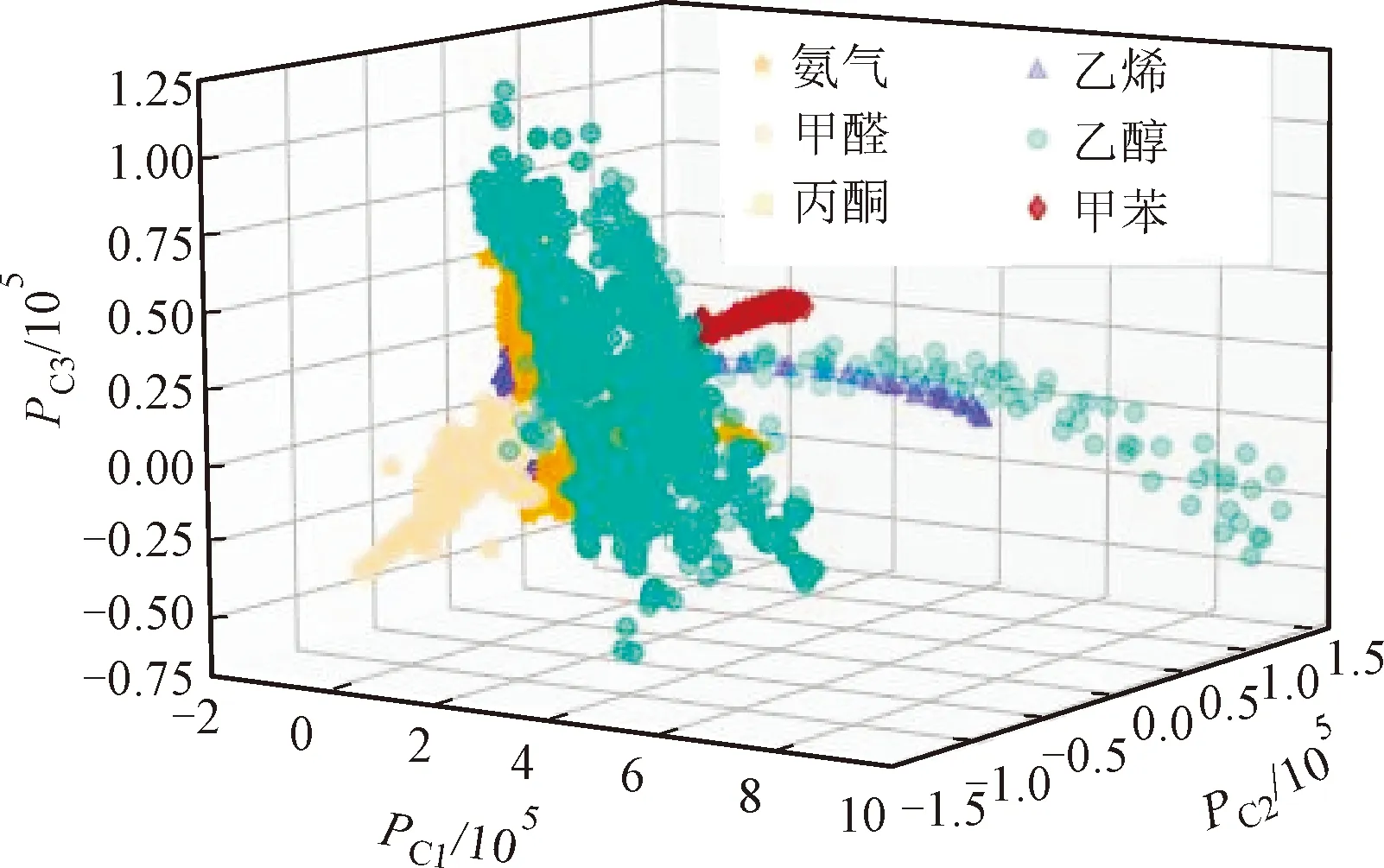
图1 n=3时PCA特征降维后的可视化结果

1.1 气体种类辨识算法比较

1.1.1 PCA降维 原数据为128维,使用PCA降维并提取贡献值之和超过99.9%的前n个特征,分别用PC1、PC2和PC3表示1维、2维、3维特征值,图1是提取前3个主成分特征的可视化结果,表明降维后气体可被分辨,其方差占比分别为90.09%、6.08%与2.49%。根据计算结果,当n=6时,数据特征已经达到99.9%,可以进行种类辨别,故KNN和CART算法均在此基础上进行。在进行维度压缩之后,能够大大简化分类的数据量,同时保留原始数据最主要得特征,消除特征之间的线性相关,加快训练时间[7]。

1.1.2 KNN、CART、MLP算法分析 对于KNN算法,决定模型优劣的参数有2个:近邻个数和距离度量参数p(p=1时为绝对距离,p=2为欧几里得距离),将数据集按照7∶3的比例分为训练集和测试集,在训练过程中采用了一折交叉验证法[8-10]。图2为p=1,2时,所有样本的训练集、验证集、测试集与总集的辩识准确率随近邻数k的变化趋势。从图2中可以看出,k=1且p=1时,KNN算法对6种组分的分类效果达到最佳。由于所测试的组分的类型是确定的,因此可以根据每种组分的测试,使用同样方法设定不同的最优测试参数。

(a)p=1

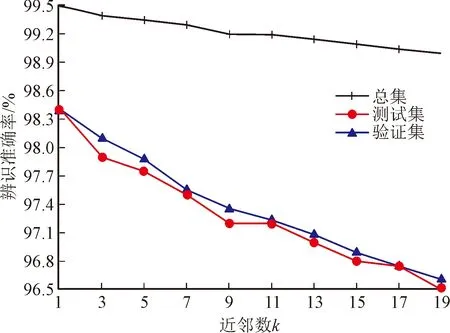
(b)p=2图2 两种p参数下6组分的总辩识准确率随近邻数k的变化情况

CART算法的分类效果与算法选择的终止条件有关。本文选择的终止条件为使每一个叶子结点的样本都为同一类,依然按照6个特征值和7∶3的比例划分数据集[11-12]。

MLP神经网络的映射方式为主动映射,无需事前揭示描述这种映射关系的数学方程,它的学习规则是使用梯度下降法。数据样本量越大,训练效果越好,所以训练时将128维特征全部输入[13-15]。使用多层神经网络进行预测的时候,需要在每一层都尽可能多的提取到数据的特征,因而需要对数据进行预处理。这里分别采用Min-Max Adam(MMA)、Min-Max RmsProp(MMR)、Min-Max Momentum(MMM)、Min-Max SGD(MMS)、Z-Score Adam(ZSA)、Z-Score RmsProp(ZSR)、Z-Score Momentum(ZSM)和Z-Score SGD(ZSS)这8种方法对包含1个隐含层的神经网络进行训练,根据图3可知,最优的组合为ZSA算法。表2显示了3种算法得到的分类效果。

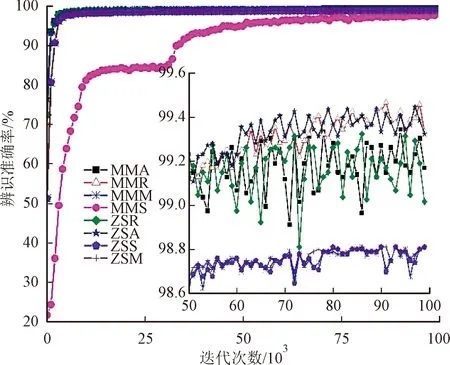
图3 不同数据预处理方法的辨识准确率

表2 3种算法分类准确率比较

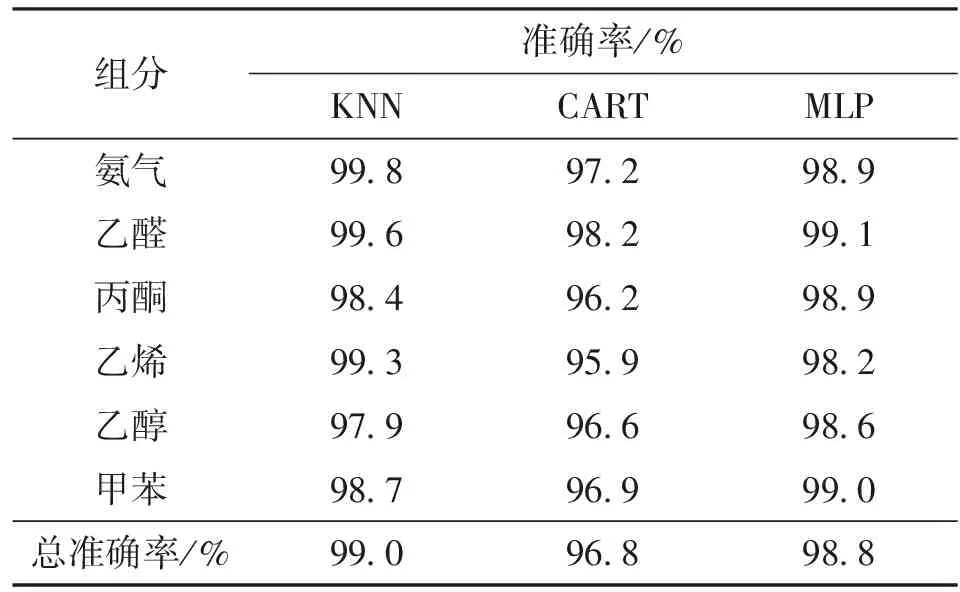
组分准确率/%KNNCARTMLP氨气99.897.298.9乙醛99.698.299.1丙酮98.496.298.9乙烯99.395.998.2乙醇97.996.698.6甲苯98.796.999.0总准确率/%99.096.898.8

1.1.3 分类算法小结 3种算法中,KNN与MLP算法均在测试集上获得了超过98%的辩识准确率,而CART算法的气体辩识准确率只有约96%。这是因为,CART算法在每次决策时,只考虑1个维度的特征,而不考虑维度之间的关联度。此结论目前只在所选的样本实例中进行了验证,理论上可应用于同类型其他样本。

1.2 UCI组分浓度预测

针对已经判定好类别的组分,使用回归算法,对气体浓度进行预测,并采用最小二乘回归中的相关系数值来评估回归分析的好坏。分别使用了线性回归、KNN回归、CART回归和MLP回归算法对6种组分的浓度进行分析,给出最好与最差的预测效果图,并列出以R2为衡量指标的预测效果对比表。

1.2.1 几种回归算法分析 首先使用PCA算法对原始的128维数据降至10维,同时将原始样本集按照7∶3的比例划分为训练集与测试集,分别绘制出6组分的真实浓度与预测浓度之间的关系,利用线性回归来判断数据之间是否有相关性,从而说明能够利用算法进行回归预测。

线性回归对6组分的预测效果相似,因此只需给出预测结果中线性相关程度最高和最低的,分别为乙烯与甲苯,如图4a、图4b所示。预测结果说明所提取的特征与浓度之间有一定相关性,但不是简单地线性叠加关系,而是包含了更高次的关系,因此本文使用了其他方法对组分浓度进行预测。

本文使用KNN算法进行回归预测,将原始样本集按照7∶3的比例划分为训练集与测试集。图5显示了使用KNN算法对甲苯和丙酮的预测效果,其R2值分别为0.998 2和0.853 1,其余的4种气体也均达到了0.97以上,获得了比较好的预测结果。KNN算法的最大优点是对异常值不敏感,缺点是样本不平衡问题(即有些类别的样本数量很多,而其他样本的数量很少),无法给出数据的内在含义,需要记录整个样本数据,硬件实现困难。

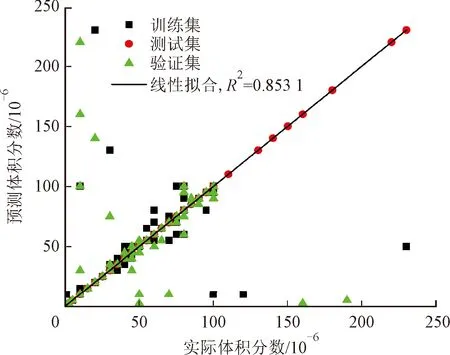
(a)甲苯

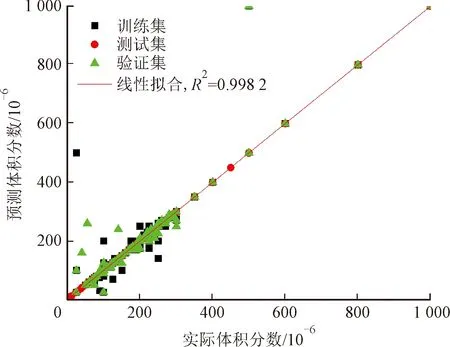
(b)丙酮图5 使用KNN算法的预测结果

KNN算法通过比较样本距离进行回归,得到的预测结果较好,因此可以尝试使用与KNN回归思想相似的CART回归算法,其基本思想是将样本空间细分成若干子间,子空间内样本的输出y(连续值)的均值即为该子空间内的预测值。图6为CART算法的预测结果,由图6可以见:CART算法对丙酮的预测效果最佳,其R2值达到0.986 0,对甲苯的预测效果最差,只有0.838 4;整体预测效果好于线性,低于KNN算法。原因在于每次决策仅仅考虑了1个属性对预测值的影响,而不考虑属性之间隐含的关联关系,故预测效果会略差,并且生成的树过为庞大的话,不利于后续规则的提取,因而一般情况下可以选择将CART分类算法作为回归之前的一个预处理过程,在出现数据阶段性波动的情况下,先进行梯度判断分类,再进行阶段回归。

(a)甲苯

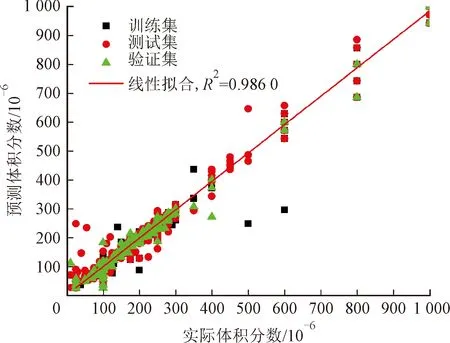
(b)丙酮图6 使用CART算法的预测结果

在尝试了上述3种方法之后,本文使用较经典的包含2个隐含层的神经网络进行回归预测[16-19]。其中输入为128维的向量,输出为1个浓度值,并选择ReLu函数作为隐含层激活函数,输出层不使用激活函数。为了加快训练效率,训练方法采用Adam算法。在进行训练前,对数据进行Z-Score归一化,然后依次训练6个网络,对6组分的浓度进行预测,选出其中回归预测效果最好的和最坏的,结果见图7。6组分的R2都大于0.9,预测效果较好。

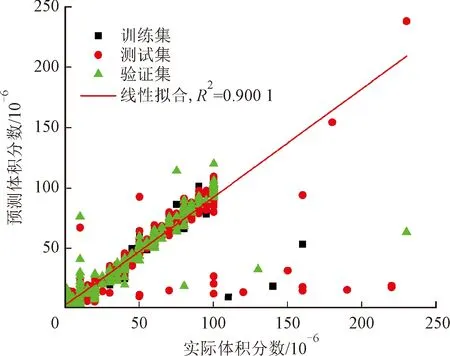
(a)甲苯

(b)丙酮图7 使用包含一个隐藏层的MLP网络的预测结果

1.2.2 回归算法总结 4种回归算法的预测效果如表3所示。由表3可以看出:线性回归算法的结果较差,说明传感器的特征与气体浓度之间有高次依赖关系;其他3种算法中,KNN回归与MLP回归在准确度上有较大优势,因而在对实验数据的分析上我们将选用这两种算法进行尝试。

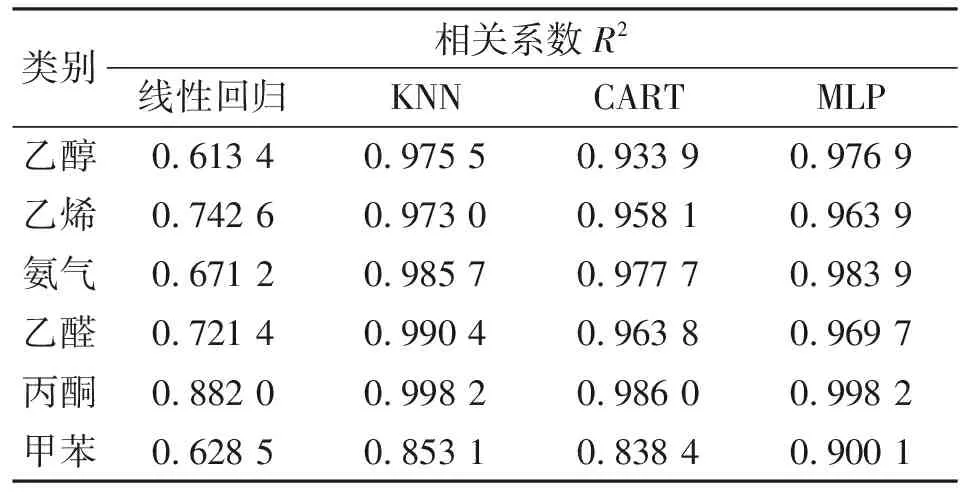
表3 4种回归算法的精度对比

2 天然气数据浓度回归算法分析比较

2.1 数据集介绍

实验数据总共4 238个,在实验腔室内4组分混合气体(甲烷、乙烷、丙烷、氮气)条件下获得3个传感器(1号为甲烷传感器,2号为丙烷传感器,3号为不同型号的丙烷红外传感器,均来自Premier公司)的读数,设定甲烷的实际体积分数测量范围为0%～100%,乙烷设定为0%～25%,丙烷设定为0%～10%。特征值为3个传感器的读数以及测试腔室内的温度和压力补偿值,输出为预测的甲烷,乙烷、丙烷之和以及氮气的体积分数。表4列出了混合气体部分样本数据。

表4 混合气体部分样本数据

2.2 KNN算法回归预测结果

采用1.2节的回归算法进行测试。图8为使用KNN算法对混合气体浓度的预测结果,图中部分数据点存在较大误差是由于实验过程中不可避免的人为操作,以及传感器读数存在一定幅度摆动所致。

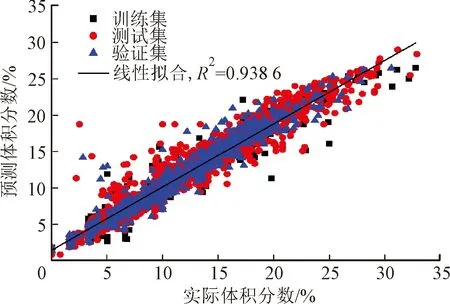
(a)甲烷

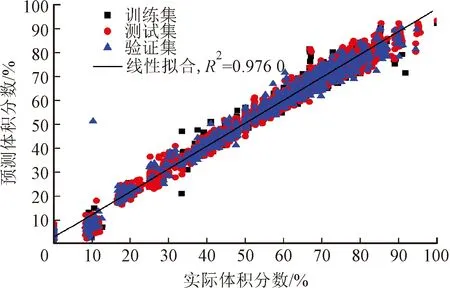
(b)乙烷、丙烷之和

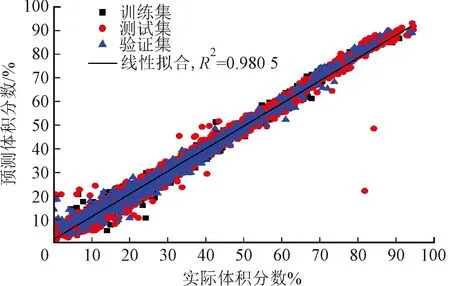
(c)氮气图8 使用KNN算法对混合气体浓度预测结果

2.3 MLP算法回归预测结果

与2.2节处理方法类似,神经网络结构为5输入(3个红外传感器读数,温度与压力补偿)3输出(甲烷,乙烷、丙烷之和及氮气的体积分数)。根据具体数据情况,经比较,决定采用Z-Score归一化进行样本预处理,采用MLP优化算法,预测结果如图9所示。

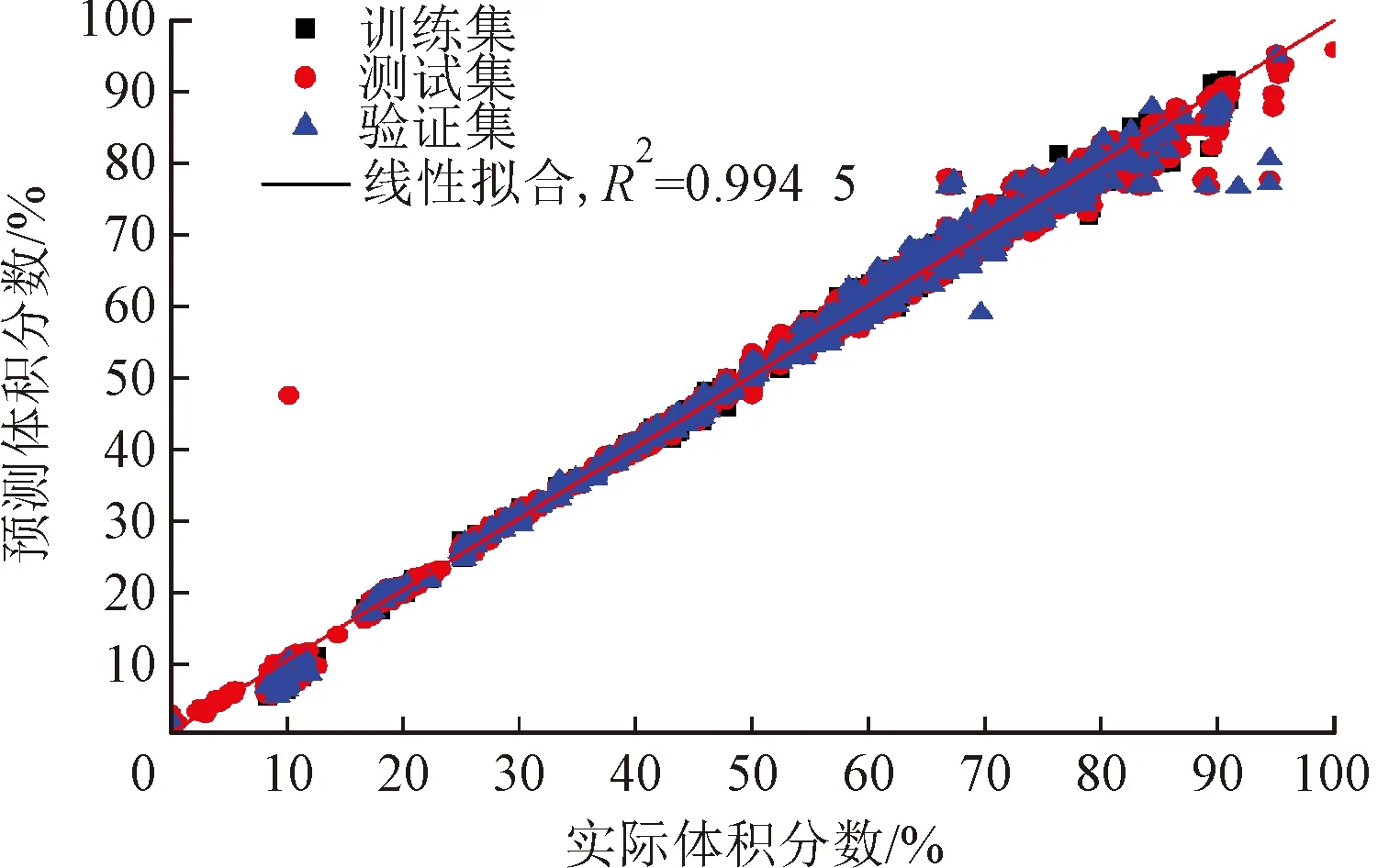
(a)甲烷

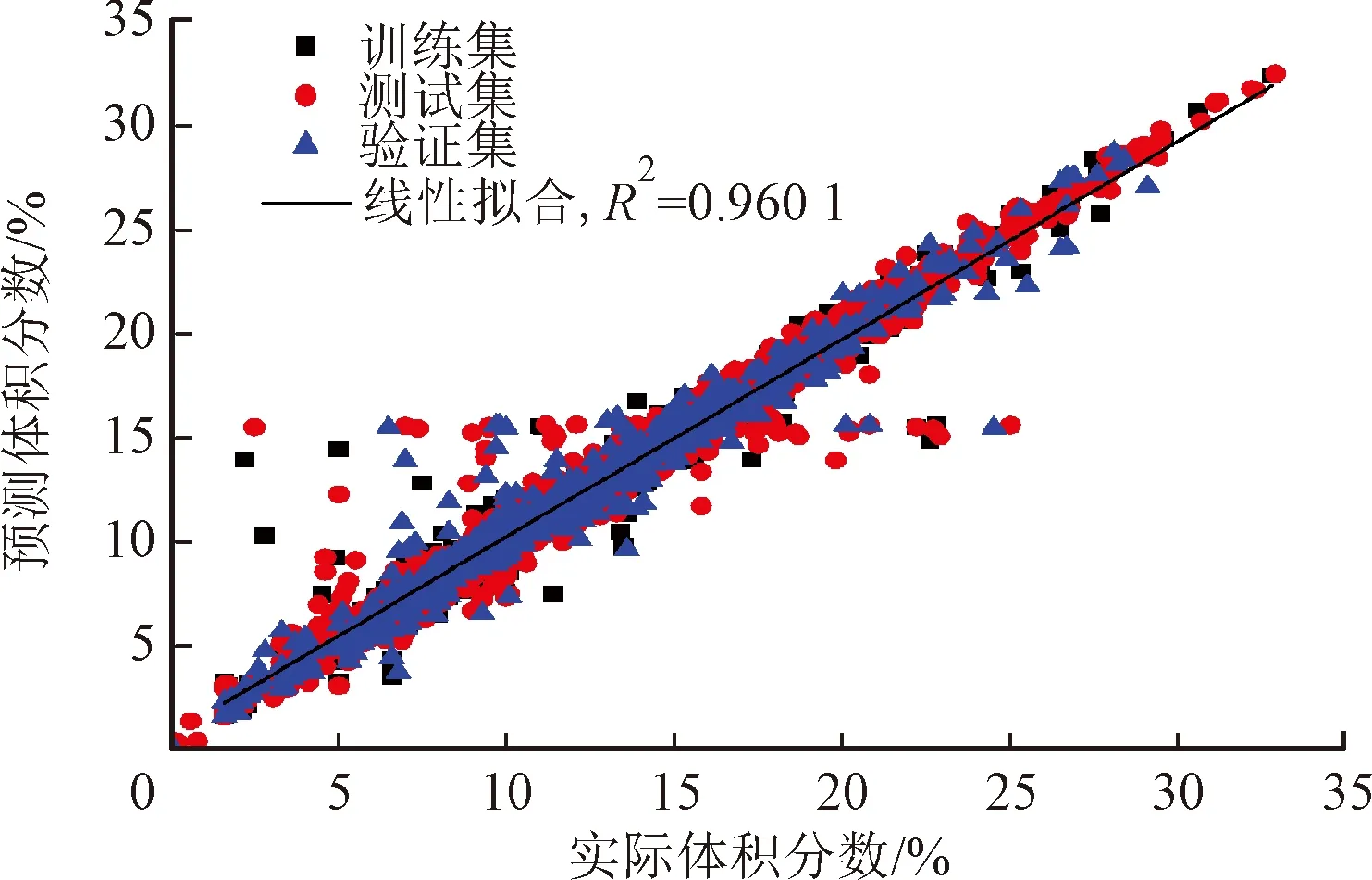
(b)乙烷、丙烷之和

(c)氮气图9 使用MLP算法对混合气体浓度预测结果

综合考虑,使用MLP算法的预测结果更佳,MLP回归算法的预测准确性高,可调参数多,优化空间大。作为电子鼻设备的优化方案,只需要记录训练模型的权值与偏置,硬件可实现。

3 结 论

本文采用KNN、CART和MLP这3种分类算法对UCI数据样本库中的6种单一组分进行了分类预测,结果表明,KNN与MLP算法对类别辨识的准确率均达到了98%以上,CART算法的准确率为96.98%。对不同种类的气体数据进行了线性回归、KNN回归、CART回归以及MLP回归网络4种算法进行筛选,并采用相关系数R2对回归效果做出评估。结果发现,KNN算法对除甲苯以外的气体的浓度辨识效果均最好,而MLP网络对甲苯的辨识效果最佳。将筛选得到的KNN与MLP回归算法用于实验室样本,也达到了较好的回归预测效果,其中使用MLP算法对甲烷、非甲烷总烃和氮气进行预测,拟合得到的回归系数的R2分别达到0.99、0.96和0.99。最终得出结论,KNN算法和MLP算法对天然气以及VOCs数据集的分类效果较好,MLP算法在浓度回归上有较大优势。将KNN算法所得最优相关模型(KNN的整个训练样本及分类规则)或相关参数(MLP的偏置与权重)利用可编程硬件进行存储,便可在在线监测设备中使用。