一种对抗欺骗式干扰的组网雷达功率分配方法

于恒力,张林让,刘洁怡,李强,赵珊珊

(1.西安电子科技大学雷达信号处理国家重点实验室,710071,西安;2.南京邮电大学电子与光学工程学院,210023,南京)

组网雷达系统能够充分发挥多雷达数据融合的优势,利用冗余信息,实现对欺骗式干扰的有效对抗。目前,组网雷达系统抗欺骗式干扰方法中,利用真假目标的空间分布差异及真假目标接收信号矢量之间相关性的差异对欺骗式假目标进行有效识别,并取得了诸多研究成果[1-7]。文献[8]给出一种典型的基于参数估计的有源假目标鉴别方法,通过组网雷达系统对欺骗式干扰的干扰参数进行联合估计,迭代寻优完成欺骗距离参数的估计,以此估计值对有源假目标进行有效鉴别,仿真验证了该方法的有效性。该模型中假设组网雷达系统总功率恒定,各发设站的发射功率相同。然而在某些应用场景下,比如组网雷达网络能量有限,或者军事应用中低截获需求等[9],则需要组网雷达系统对各节点雷达功率进行优化,使其在能量限定的情况下发挥出最优的抗干扰性能。

近年来,相关学者对组网雷达系统资源优化问题进行了大量研究,文献[10-13]研究了多站雷达系统对目标进行定位和跟踪过程中的功率分配方法,表明相对于功率均匀分配的情况,通过相应功率分配算法对组网雷达发射站进行最优功率分配后,能够明显提高多站雷达系统对目标的定位及跟踪精度。文献[14]在欺骗式干扰环境下,提出一种针对组网雷达系统的优化布站方法,在利用数据级融合对抗欺骗式干扰的过程中,通过优化布站实现组网雷达被欺骗概率最小化和其覆盖范围最大化,从而达到最优的资源利用方式。文献[15]研究了多目标跟踪下的分布式MIMO雷达资源优化问题,计算了在任意雷达布阵形式下系统的最少资源需求量。然而,在现有组网雷达抗欺骗式干扰方法中,尚未考虑通过功率分配方法提高抗干扰性能的问题,因此,研究欺骗式干扰下如何对组网雷达系统进行功率分配具有重要意义。

针对上述问题,本文提出一种欺骗式干扰下组网雷达功率分配方法,首先计算出在联合检测下,对欺骗式干扰的欺骗距离进行参数估计时的克拉美罗下界(CRLB),通过CRLB分析得到欺骗式假目标与真目标的鉴别门限,构建鉴别器对欺骗式假目标进行鉴别;在此基础上,以假目标鉴别概率为目标函数对组网雷达系统进行功率分配,得到指定总发射功率情况下,使假目标鉴别概率最大的最优发射站发射功率分配方式;最后,对组网雷达的功率分配方法进行仿真分析。仿真结果表明,本文方法可有效提高组网雷达系统对假目标的鉴别概率。

1 系统数学模型分析

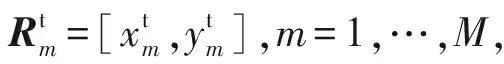
假设真实目标位置坐标为XT=[x,y],τmTn表示从发射站m发射信号照射到目标再反射回到接收站n的传输时间

τmTn=rmTn/c

(1)

式中:rmTn为发射站m到目标与目标T到接收站n的距离和。

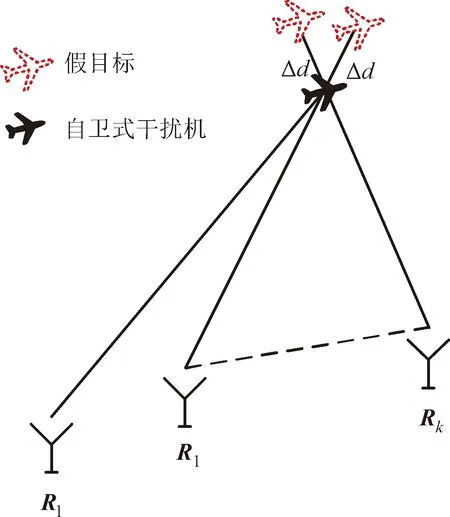
图1 雷达多站系统下欺骗假目标示意图

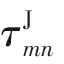
(2)

式中:Δd表示干扰机施加的欺骗距离参数。在Δd=0时,欺骗式干扰模型也可以表示真实目标回波。因此,可将任意一个接收站n中的回波信号统一建模为

(3)

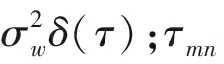
对于真目标和欺骗式假目标而言,Δd是分辨真假目标的有效参数。真目标其物理位置是空间固定的,不存在欺骗距离,Δd为0。然而,对于转发式假目标,干扰机为了对雷达站进行欺骗式干扰,施加了时间延迟,Δd不为0。所以,利用组网雷达系统对Δd作估计参数可以有效鉴别欺骗式假目标,从而达到抗欺骗式假目标的目的。

2 欺骗距离参数克拉美罗界推导

对于任意一个无偏估计量,克拉美罗下界(CRLB)可以表示其估计方差的最低界限[16]。对于组网雷达系统而言,真目标及欺骗式干扰的未知参数为θ=[x,y,Δd,h]T,其中h=[h11,h21,…,hmn,…,hMN]T,T表示矩阵转置符号,则位置参数的无偏估计满足

(4)

式中:Eθ[·]表示θ的期望;J(θ)为费谢尔信息矩阵(FIM),具体可表示为

(5)

式中:p(r|θ)为θ条件下,观测量r的联合概率密度函数,未知参数θ的克拉美罗界可以定义为

CCRLB=J-1(θ)

(6)

由式(3)可知,时延参数是目标位置参数(x,y)的确定函数,为了计算简便,定义一个新的未知参数ψ=[τ,h]T,根据链式法则可以得到

J(θ)=PJ(ψ)PT

(7)

式中:矩阵J(ψ)为观测量r在ψ条件下的费谢尔信息矩阵,可表示为

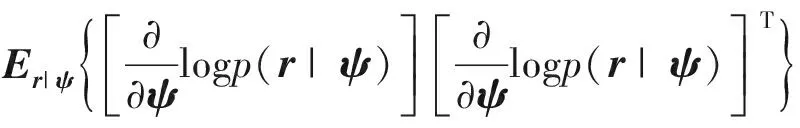
(8)

文献[17]中推导了费谢尔信息矩阵J(ψ)的表达式,这里不再赘述。仿照文献[16],矩阵P的雅可比行列式计算方法为

(9)

矩阵H为式(2)中的时延量对参数x、y和Δd的偏导矩阵

(10)

式中:atm=xm-x/RTmx;RTmx为发射站m到目标的距离;btm=ym-y/RTmx;arn=xn-x/RRnx;RRnx为接收站n到目标的距离;brn=yn-y/RRnx。

将式(10)和式(11)代入式(9)和式(8),可以得到被估计参数的克拉美罗界为CCRLB。

取CCRLB矩阵中左上角3×3的矩阵即可得到参数x、y、Δd的估计精度,经过计算,可表示为

(11)

矩阵A中各元素具体为

A12=A21=

A12=A21=

由式(11)可以看出,CCRLB矩阵中各元素与各发设站发射功率、各通道回波强度,及目标(或干扰)与各节点雷达的相对位置有关。

3 基于功率分配的假目标鉴别算法

3.1 假目标鉴别算法

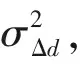
(12)

式中:|A|为矩阵A的行列式。根据奈曼-皮尔逊准则,将参数Δd作为鉴别统计量构建鉴别器,存在2种假设:

(1)在H0假设下,欺骗距离为0,即该目标为真实目标,表示为H0;

(2)在H1假设下,欺骗距离不为0,即该目标为欺骗式假目标,表示为H1。

由于估计误差的存在,可以将欺骗距离Δd的估计值看为一个满足如下正态分布的随机变量

(13)

则鉴别统计量在假设H0和H1条件下的分布函数分别为

(14)

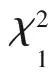
(15)

据此,可以得到有源假目标的鉴别概率

(16)

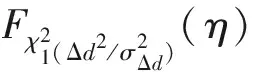
3.2 组网雷达功率分配方法

由3.1节分析可知,有源假目标的鉴别概率与组网雷达系统中各发射站的发射功率有关,因此,可将式(16)作为功率分配算法的代价函数,通过对发设站的发射功率进行最优功率分配,使组网雷达系统对假目标鉴别概率最高,优化模型可表示为

(17)

式中:1T=[1,1,…,1]1×M;Ptotal表示发设站的总发射功率;Pkmin和Pkmax分别表示第k部发射站发射功率的下限及上限。具体功率分配步骤如下。

步骤1初始化发射功率矩阵Paverage=Ptotal/M,并计算此时的假目标鉴别概率QPT(Paverage)。

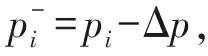
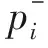
步骤4如果有任意发射站发射功率不满足Pkmin≤pk≤Pkmax,或全部发射站遍历结束,整理功率分配矩阵,结束算法。

以上功率分配方法可以表述为:在保证发射站总发射功率恒定的前提下,通过计算各发射站发射功率增减对假目标鉴别概率的影响,寻找对提高鉴别概率贡献大的发射站,将更多的功率资源分配其中,以提高假目标鉴别概率。

4 仿真实验与分析

为验证功率分配算法的有效性,并进一步分析不同参数对功率分配结果的影响,以一个由5部发射站和5部接收站组成的组网雷达系统为例进行仿真实验,5部发射站(T1～T5)的位置分别为(1,1)、(2,0)、(-2,0)、(0,2)、(1.5,0) km,5部接收站(R1～R5)的位置分别为(-1.8,0)、(1.8,0)、(0.2,0.2)、(0,1.8)、(0,-2) km,设真实目标的位置坐标为[12,15]km。实验中,各发射站除了发射功率外其他发射参数相同,载频为2 GHz,有效带宽为0.5 MHz。

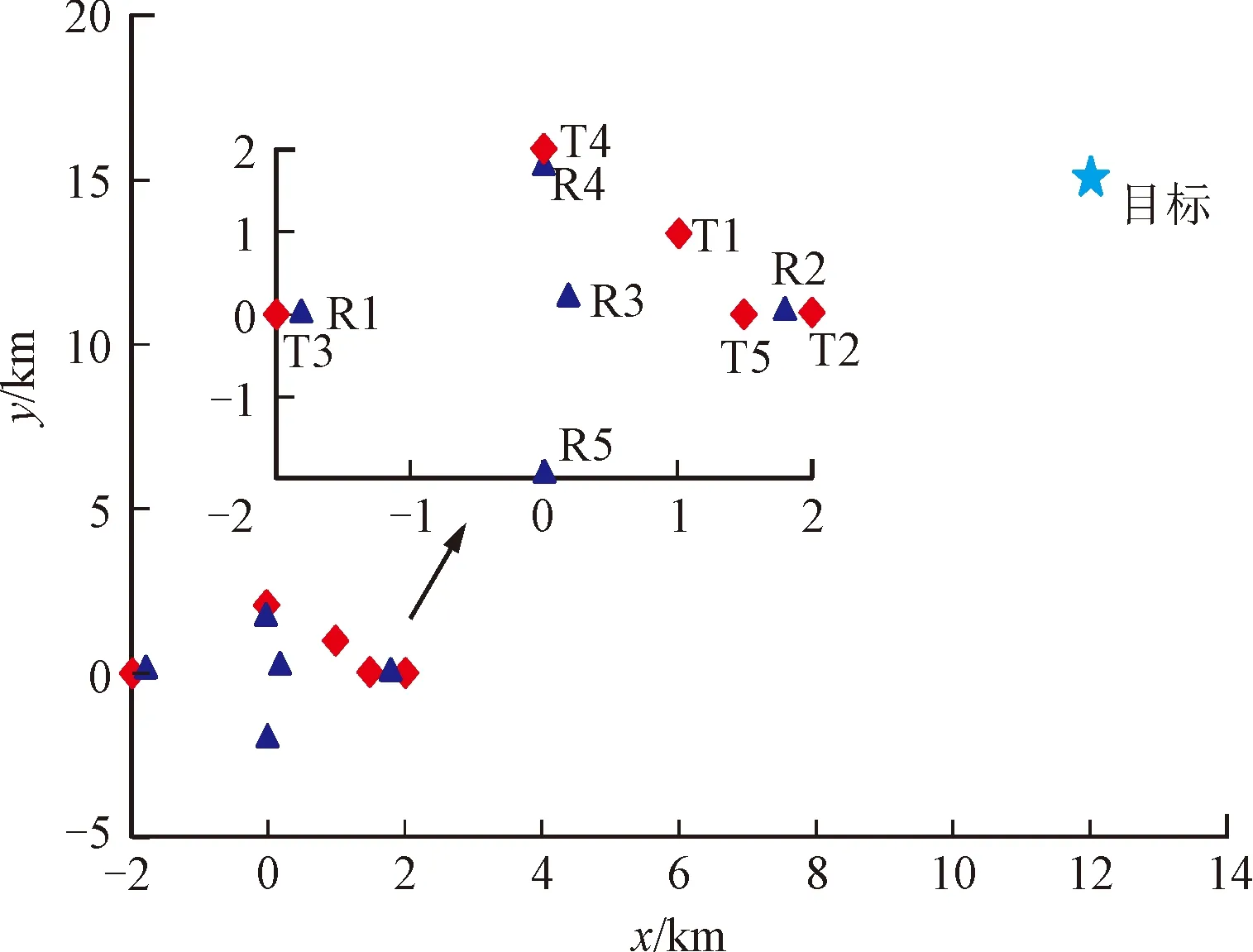
图2 节点雷达与目标的位置信息

设欺骗式假目标的欺骗距离为1 km,为了分析通道反射系数对功率分配结果的影响,设定2种不同的反射系数模型:第1种模型假设各发射站入射角度差异带来的目标RCS起伏可以忽略,即目标在各个通道的反射系数相同,设定h1=[0.5,…,0.5;…;0.5,…,0.5],此时,功率分配方式只与目标及各节点雷达的位置有关;第2种模型假设由于发射站位置不同,带来的目标RCS强度等因素的不同而导致各个通道反射系数不同。

设定h2=[h21;h22;h23;h24;h25],假设

h21=[0.75,0.5,0.55,0.65,0.5,0.45,0.35]

h22=[0.2,0.15,0.1,0.1,0.1,0.1,0.1]

h23=[0.75,0.5,0.55,0.65,0.5,0.45,0.35]

h24=[0.2,0.15,0.1,0.1,0.1,0.1,0.1]

h25=[0.75,0.5,0.55,0.65,0.5,0.45,0.35]

分别在2种不同的场景下对2种抗欺骗式假目标鉴别算法进行仿真实验,预设的真目标鉴别概率PPT为99.9%,不同条件下均通过1 000次Monto Carlo仿真实验,统计其平均得到假目标鉴别概率。实际中,目标的RCS会随着姿态的起伏而变化,尤其是运动目标在飞行过程中,雷达照射视角的变化带来RCS较大的变化,工程中施威林(Swerling)起伏模型可以作为目标RCS的统计模型,然而无法提供目标在特定环境中RCS的准确预测值。针对这一问题,文献[18]给出了一种用于雷达资源管理的目标雷达截面积预测算法:首先通过回波处理获取目标RCS的测量值,进而通过概率密度转移函数对下一时刻的RCS进行预测。因此,在实际中,可以通过类似方法对目标RCS进行预测[19-20],进而根据预测结果对组网雷达进行功率分配。

本文首先在相同信噪比下对不同反射系数模型条件下对文献[8]有源假目标鉴别算法和本文所提出算法进行仿真,得到了功率分配结果及相应的假目标鉴别概率QFT,然后在不同信噪比下,分析了2种反射系数模型下2种算法对假目标鉴别概率QFT。

4.1 仿真实验1

分别用文献[8]算法(各发射站平均分配功率)和本文所提算法进行仿真实验,表1和表2分别给出了h1和h2模型下功率分配结果及2种算法得到的假目标鉴别概率,其中:各节点雷达最低发射功率设定为30 W,信噪比为5 dB。

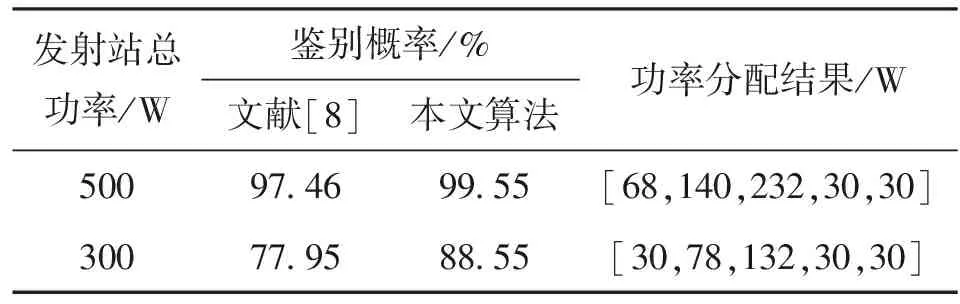
表1 h1模型下功率分配结果

表2 h2模型下功率分配结果

从表1和表2的仿真结果可以看到,在2种场景下,通过功率分配算法对组网雷达系统的发射站进行功率分配,能够有效地提高组网雷达系统对假目标的鉴别概率,尤其当发射站的总功率不充裕时,本算法对假目标的鉴别概率更明显,从而验证了本文所提出的组网雷达功率分配方法的有效性。

通过表1的仿真结果可以看出,在各通道反射系数相同的条件下,本文所提出的功率分配算法倾向于将组网雷达系统的发射功率分配到发射站1、发射站2及发射站3,这是因为,发射站2和发射站3组成的“孔径”最大,可以得到相对探测区域的最大空间角度差异,而空间角度的差异越大,数据融合对欺骗式假目标的鉴别效果越好。因此其获得的功率资源更多。

当反射系数模型改变后,通过表2的仿真结果可以看出,发射站2及发射站4对应的反射系数较其他发射站低,意味着其信号路径损失更严重,通过表3可以看出,在这种情况下,大部分功率资源更倾向于分配到信号反射系数更高的发射站1、发射站3及发射站5。

4.2 仿真实验2

本实验主要为了验证本文所提算法与现有算法相比的优势。采用本文方法与文献[8]方法仿真对比其组网雷达系统对假目标的鉴别性能。图3和图4分别给出了h1和h2条件下有源假目标鉴别概率随信噪比的变化曲线,仿真中设定的组网雷达总功率为500 W。图5给出了h1条件下本文算法得到的假目标鉴别概率随着延时距离的变化曲线。

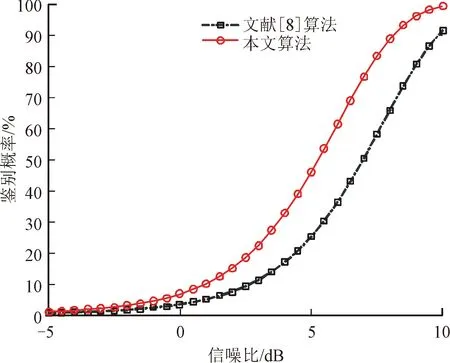
图3 h1模型下有源假目标鉴别概率

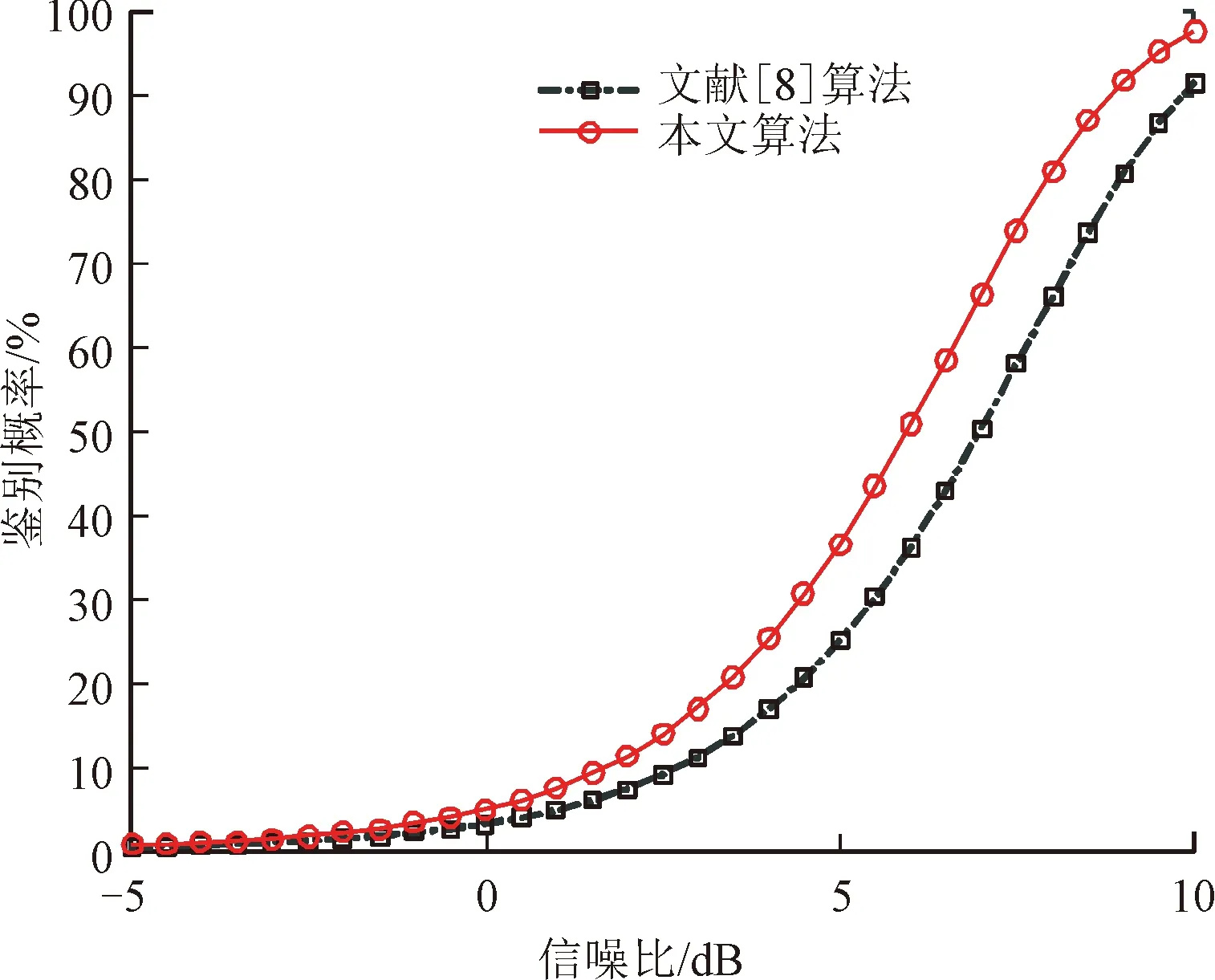
图4 h2模型下有源假目标鉴别概率

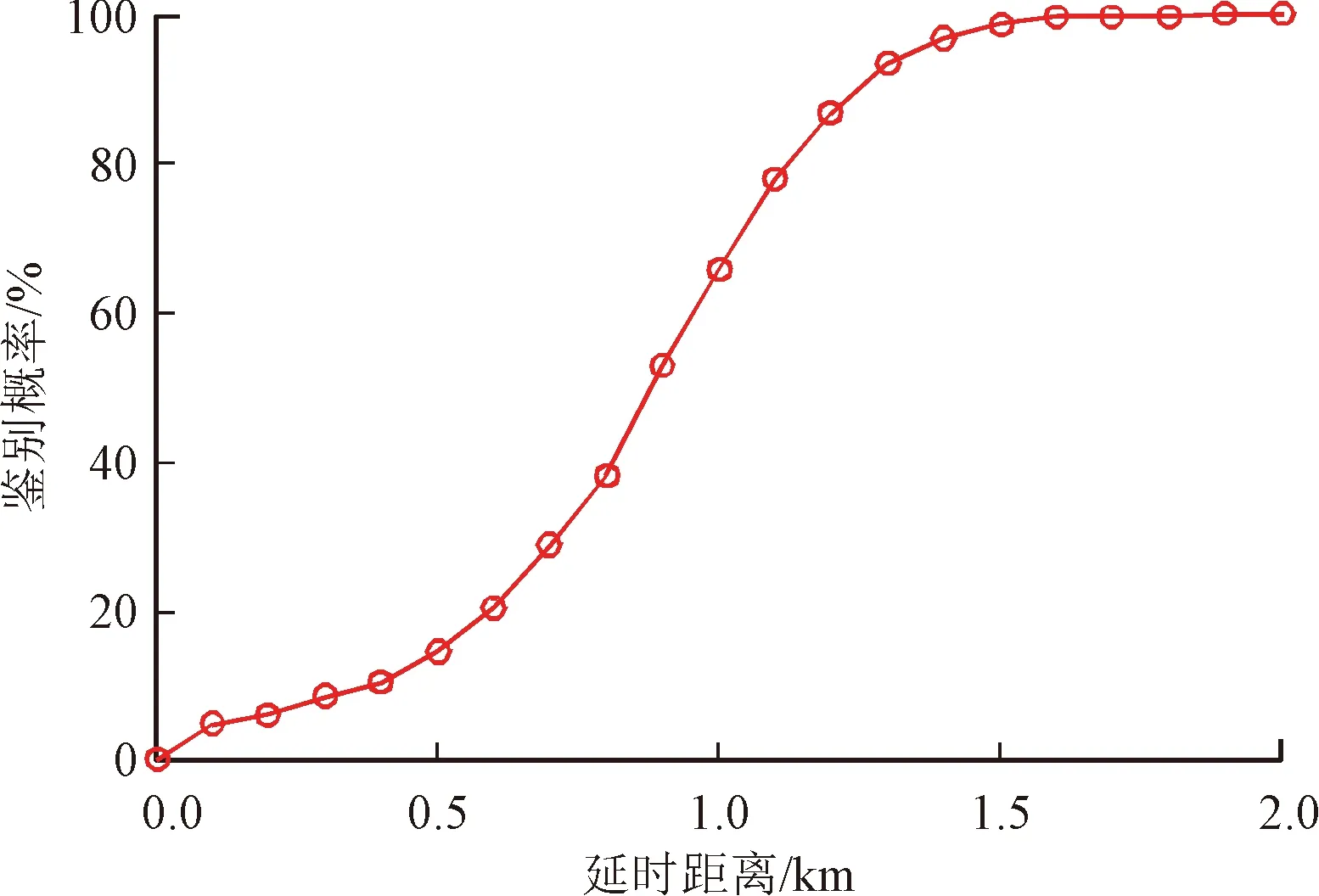
图5 有源假目标鉴别概率与延时距离的关系曲线

从图3、图4的仿真结果可以看出,在2种条件下,随着信噪比的提高,文献[8]算法和本文算法对有源假目标的鉴别概率变大,因为在联合检测下,较高的SNR会带来估计精度的提高。同时可以看出,组网雷达系统通过本文提出的功率分配方法进行资源分配后,能够明显提升对有源假目标的鉴别概率。从图5可以得到:随着延时距离的增加,假目标鉴别概率逐渐提高,这是因为随着欺骗距离的增加,假目标鉴别统计量的非中心参数增大,与真目标差异增加,因此欺骗式干扰被判别的有效性增加。

仿真实验表明:在组网雷达系统通过估计欺骗距离参数来鉴别欺骗式假目标的过程中,假目标鉴别概率受发射站发射功率分配方式的影响,发射站功率平均分配并不是最优选择,而本文所提出的功率分配方法可保证更多的功率资源分配到对目标空间角度差异大及回波信号路径损失较低的发射站中,相较于现有算法,本文所提方法能够有效提高假目标的鉴别概率。

5 结束语

本文首先分析了现有组网雷达系统鉴别欺骗式假目标算法存在的问题。在此基础上,提出了一种欺骗式干扰下组网雷达系统功率分配方法。通过理论分析得到假目标鉴别概率,并以此为目标函数对发射站发射功率进行功率分配。仿真实验证明了本文方法能够明显提高假目标鉴别概率,尤其在组网雷达系统功率不充裕时,提升效果更加明显。