基于非饱和蠕变模型的滑坡长期变形数值模拟

王 力，王 琳，王世梅，郭 飞，邹良超

(1.三峡大学 三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；2.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌 443002)

1 研究背景

滑坡是一种常见的地质灾害，而降雨和水库蓄水是滑坡失稳的主要诱因。大量实例表明，水库蓄水导致滑坡变形演化失稳并不是立即发生的，大都经历了一个时间发展过程[1-2]。如美国Grand Coulee水库在1941年蓄水后的12 a内，先后发生滑坡500起，其中49%起发生在蓄水后2 a内，51%发生在2～12 a之间[1]；我国三峡水库自2003年开始蓄水以来诱发变形的滑坡有151起，累计最大位移超过1 000 mm的大型滑坡达14个，绝大多数滑坡变形随时间在不断增加。如树坪滑坡累计最大位移量达到4 300 mm，随着库水位周期性涨落，滑坡体地下水呈现周期性升降，地表位移变形速率也呈周期性降低和增大，但滑坡累计位移总体上呈阶梯状持续增大趋势，即使库水位和地下水位稳定期间其变形仍在持续增大。这说明滑坡变形演化过程不仅与库水变动产生的渗流作用相关，还与蠕变效应相关。实际滑坡变形演化预测常采用现场监测和物理模型试验进行，但这2种方法主要用于重大滑坡研究，实际应用并不广泛。具有蠕变特点的滑坡从启动到整体滑动这一过程存在阶段性的变形，基于非饱和流固耦合理论的数值方法对于此类滑坡的分析尚有不足，因此需将渗流与蠕变耦合来分析库水作用下滑坡体内实际力学过程。 目前国内外对土体蠕变研究以试验为主[3]，针对蠕变的数值计算研究较少。谢宁和孙钧[4]提出了一种能方便有效地求解土非线性蠕变问题的二次初应变法，该方法在时步上仍采用与线性蠕变问题相同的黏性初应变法，而在每一时步，采用非线性弹性初应变法，通过反复迭代，求解非线性平衡方程，最终得到每一时步非线性蠕变的解。主要的商业数值计算软件也提供了部分蠕变计算模型，如FLAC提供了经典黏弹性模型(马克斯韦尔体)、伯格蠕变模型、二分量幂定律等蠕变模型[5]；ABAQUS提供了3种可供用户输入相关参数来定义的蠕变模型：时间硬化蠕变模型、应变硬化蠕变模型和Singh-Mitchell蠕变模型[6]。但是一般商业数值软件中提供的蠕变模型相对较少，参数难以确定，且极少有考虑非饱和条件的蠕变模型或二次开发接口，因此对于许多实际工程问题往往需要自行编程求解。

本文基于前期研究建立的适用于非饱和土的非线性蠕变模型及其三维形式[7]，采用试验数据对模型进行验证，研究了基于该非饱和土蠕变模型的数值计算方法，并编制了渗流及蠕变耦合计算的有限元计算程序；利用该程序对三峡库区树坪滑坡在库水位变动下的变形过程进行了数值模拟，并与实际监测资料进行了对比分析。该项研究可望为分析非饱和土的长期强度和变形、预测在库水和降雨作用下滑坡的长期稳定性提供一种新理论和新方法。

2 基于伯格模型的非饱和蠕变模型

2.1 蠕变模型介绍

目前，宏观蠕变模型大致可以分为3类：经验-半经验模型、基于一般流变理论的元件模型、黏弹塑性模型。本文根据团队成员试验结果[7-9](不同基质吸力的流变曲线)探究含有基质吸力的变量——净围压对非饱和土流变的影响规律;根据非饱和蠕变曲线特征，类比饱和蠕变模型的建模思想，将净围压作为一个新的应力变量加以考虑，研究净围压与应变之间的关系。从而将基质吸力反映在蠕变模型中，得出能够同时反映应力-应变-时间-基质吸力的非饱和土蠕变模型[7]，即

2.2 模型参数求解及检验

扩展的伯格蠕变模型中含有负指数项，其参数一般需要采用非线性最小二乘法进行回归求得，但是利用非线性最小二乘法进行回归常常会得到不同的结果，即参数存在多组不同的匹配。在本文中，所建模型的参数都具有较明确的物理含义，因此可根据其物理意义及蠕变曲线特征先求一组接近实际值的初值，然后利用非线性回归算法进行回归求得模型参数，以避免回归过程中参数的跳跃，扩展的伯格蠕变模型参数初值的求解公式为[10]

εij=A+2aC(1-e-Dt) 。

(2)

其中，

对式(2)取对数，有

ln(εij-A-2aC)=ln(-2aC)-Dt。

(3)

可得

εij=A+a[Bt+C(1-e-Dt)+E(1-e-Ft)] 。

(4)

式中A，B，C，D，E，F均为待求系数。

式(4)在对数坐标系中为一直线方程，A已确定，D即为直线的斜率，再将D值代入式(2)即可解出C。由此可确定一组初值，再在MatLab中利用lsqcurvefit非线性回归工具可回归出A,B,C,D,E,F的稳定解。由于μ值的大小对其他参数的影响很小[11]，本文中根据经验μ值取0.4。

按上述参数求解方法求解模型的所有参数。限于文章篇幅,具体选取的数据分别为围压σ3=250 kPa、ua=200 kPa和围压σ3=300 kPa、ua=200 kPa共2组。求得应力-应变双曲线函数的参数如表1所示。

表1 应力-应变双曲线函数参数

注：Su为不排水剪切强度;(σ1-σ3)f为实际破坏剪应力。

表2 各组围压下模型参数及相关系数

将求得的应力-应变双曲线函数的参数代入式(4)，按上述方法求取参数初值，再利用非线性最小二乘法回归，即可得到模型各组净围压下蠕变模型的参数，并求取决定系数R2，结果如表2所示。

从表2可知，上述蠕变模型的模拟效果比较好，与试验数据的决定系数基本都在0.96以上，各级净围压下，模拟蠕变曲线与实际试验值比较吻合，说明上述蠕变模型可以较好地模拟滑带土的蠕变特征。

3 非饱和渗流与非饱和土蠕变耦合计算有限元程序编写

3.1 求解策略

在非饱和蠕变过程中，随着土体中含水量的变化，基质吸力对蠕变性质影响较大，从本文所建立的模型也可以看出基质吸力在蠕变模型中为一个重要参数。而土体中的基质吸力与土体中含水量的变化息息相关，即与土体中的非饱和渗流过程密切相关。因此在求解非饱和蠕变模型时，需要同时进行非饱和渗流计算。

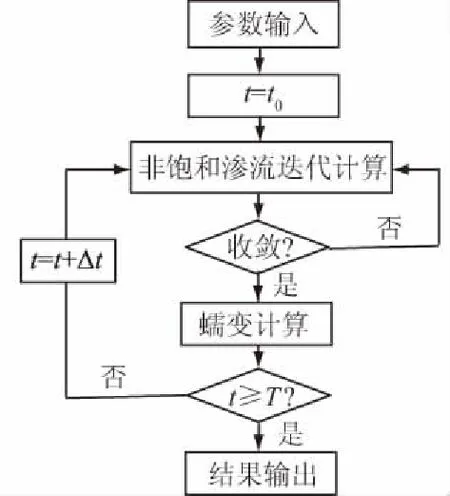
图1 渗流与蠕变耦合计算流程

考虑到蠕变模型与非饱和渗流方程(Richards方程)的相对独立性及两者都与时间相关，可以将非饱和蠕变模型和非饱和渗流方程分开求解，即：在同时间步中先计算非饱和渗流方程，并将计算得到的负孔隙压力(基质吸力)及渗透压力荷载加入土体的蠕变计算中，计算该时刻的蠕变变形；然后进入下一时步，依次循环，直到在指定时间域计算完毕。渗流与蠕变耦合计算流程如图1所示。值得指出的是该求解策略考虑了非饱和渗流对蠕变变形的影响，而忽略了蠕变变形对非饱和渗流的影响。

3.2 渗流蠕变耦合主要子程序

3.2.1 INPUT子程序

INPUT子程序主要读取单元、节点、参数、渗流初始条件、边界条件及控制信息，为计算处理好所有的计算参数。

3.2.2 UNSATURATED_SEEPAGE子程序

UNSATURATED_SEEPAGE子程序为计算土体的非饱和渗流过程的主程序，计算出各个时间步各节点的水头、负孔隙水压力及渗透力。

3.2.3 CREEP子程序

CREEP子程序为蠕变计算的主程序，调用非饱和渗流的计算结果，计算出各个时间步的位移场及应力应变场。

3.2.4 SOLVE子程序

SOLVE子程序主要用于求解组装后的线性方程组，本程序采用共轭梯度法。由于在本程序中非饱和渗流计算需要在各个时步进行多次迭代，求解各时间步位移场时也需要依次求解，调用频率较高，其计算效率及正确性直接决定本程序的总体效率和正确性。

3.2.5 OUTPUT子程序

OUTPUT子程序主要输出程序的计算结果，具体为在每时间步计算完毕后将计算结果如总水头、孔隙水压力、位移场、应力应变场按照Tecplot软件的文本格式输出相关信息，以便用Tecplot软件打开，进行后处理。

为了验证本程序的正确性和可靠性，分别选用具有试验数据的非饱和渗流算例及非饱和三轴蠕变试验进行计算，以检验有限元程序的正确性。

3.3 非饱和渗流有限元计算程序验证

非饱和渗流的验证算例采用赤井浩一等[12]做的模型试验。试验模型为315 cm×23 cm×33 cm(长×宽×高)的均质沙槽。沙槽中介质的饱和渗透系数为0.33 cm/s，体积含水量θ与负孔隙水压力h及非饱和相对渗透系数kr的关系如表3所示。

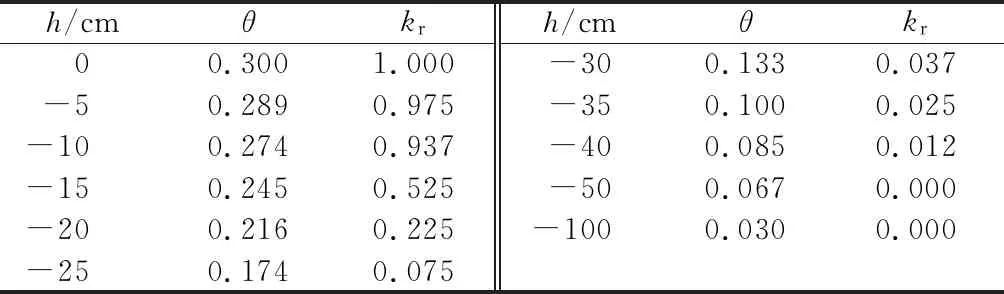
表3 土体负孔隙水压力h、体积含水量θ、非饱和相对渗透系数kr数据

现选取一种工况的试验结果与计算结果相比较。即左右两端初始水位都在离槽底10 cm处，左端水位瞬时上升至离槽底30 cm处。由于本程序维度为二维，取模型长-高截面为计算截面，剖分四边形网格如图2所示，共计节点768个，单元693个。

图2 沙槽试验计算模型网格

图3 不同时刻水位线分布

图4 试样计算模型

3.4 非饱和蠕变有限元计算程序验证

非饱和蠕变有限元计算程序的验证采用一组非饱和三轴蠕变试验数据，为了便于比较，仍采用σ′3=200 kPa，σ3=400 kPa，ua=200 kPa，偏应力水平为0.50，即偏应力188 kPa。试验用土样尺寸Φ6.18 cm×12 cm，经过轴心选取矩形截面为计算截面，剖分四边形网格如图4，共计节点325个，单元288个。

计算参数采用表1求取的模型参数，计算时长为15 000 min，时间步长参考试验采样周期，以模型顶部中间节点(节点编号为35)作为考察点，绘制该点应变曲线并与试验值进行比较，结果如图5所示。

图5 应变程序计算值与试验值及模型模拟值比较

从图5可以看出,程序计算值与三轴蠕变试验值及模型模拟值基本吻合，其中程序计算值略偏大，可能是计算时考虑了土样自重应力，说明编写的非饱和蠕变有限元计算程序正确可靠。

4 算 例

4.1 滑坡简介

选取三峡库区树坪滑坡为模拟对象，树坪滑坡为一个古崩滑堆积体。树坪滑坡分布高程约为65～500 m,纵向长度约为800 m，横向宽度约为700～900 m，滑坡前缘突入长江，剪出口高程约为65～68 m，滑体厚约40～70 m，体积约为2 600×104m3。滑坡形态总体呈下陡上缓斜坡，坡度约为22°～35°。

选取滑坡变形较大的1#滑体轴向剖面为计算截面，计算模型后边界取至滑坡后缘460 m高程处，前边界取至54 m高程处。对计算截面进行四节点矩形单元网格剖分，共剖分3 855个单元，4 010个节点(如图6所示)。模型中的左右边界条件为水平约束，底部约束条件为双向约束。地层自上而下分别为滑体(上部以粉质黏土为主，下部碎石含量较多)、滑带及基岩。

图6 树坪滑坡数值计算模型

4.2 计算参数

按照本文所建立的非饱和蠕变模型对树坪滑坡的长期蠕变变形进行数值模拟，需要的非饱和渗流参数及非饱和蠕变模型参数数目较多，若一一通过试验测定或通过参数反演则工作量巨大。本文主要分析滑坡长期变形趋势，参数主要通过以往资料进行工程类比以及根据经验值多次试算来确定。树坪所在的三峡库区存在大量涉水型滑坡，根据附近泄滩滑坡及千将坪滑坡等相关资料[13-15]以及本团队相关非饱和三轴蠕变试验参数，确定的滑体、滑带及滑床基岩的非饱和渗流参数分别为3.0,0.003,0.000 216 m/d。

滑体、滑带及滑床基岩的土-水特征曲线及渗透性函数分别如图7—图9所示。

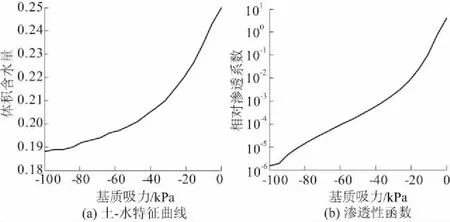
图7 滑体土-水特征曲线及渗透性函数

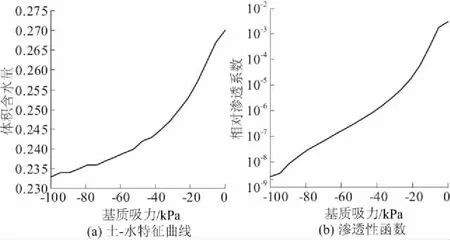
图8 滑带土-水特征曲线及渗透性函数

图9 滑床土-水特征曲线及渗透性函数

滑体、滑带及滑床基岩的非饱和蠕变模型参数如表4 所示。

表4 滑坡非饱和蠕变参数

4.3 计算工况

树坪滑坡外荷载主要有自重荷载和因三峡库区库水位升降及降雨入渗而产生的动水压力。由于每年降雨情况具有较大的随机性和离散性，本文暂不考虑降雨工况。因此计算工况主要考虑库水位的变动情况。由于每年库水调度情况大致相近，因此计算工况选取1 a时间内库水位实际调度周期(2010年6月15日—2011年6月15日)，库水位如图10所示。为了计算方便，忽略库区水位小范围的波动，对库水位的变动进行线性简化，即库水位开始在145 m左右稳定一段时间，然后从145 m上升至 160 m，之后从160 m降至145 m，再从145 m上升至 175 m，然后稳定大约75 d，再从175 m降至145 m。

图10 2010年6月15日—2011年6月15日三峡库区水位变动

4.4 初始条件

滑坡渗流边界假设底部为不透水边界，滑坡前缘与后缘给定水头边界，坡面为透水边界。计算应力应变场时，假定滑床基岩底部边界上节点水平及竖向位移约束为0，前后两侧节点水平位移为0。滑坡渗流场初始值采用库水位稳定在145 m时的渗流场，初始应力应变场则采用在自重应力及初始渗流场作用时计算所得的应力应变。为了使得非饱和渗流计算与蠕变计算同步，在非饱和计算中，基质吸力对孔隙水压力有显著的影响，所以设置不同时刻的孔隙水压力，根据渗流场、位移场在初始时刻孔隙水压力分布云图来分析渗流场的变化。初始状态渗流场及位移场孔隙水压力分布云图如图11所示。

图11 初始时刻滑坡孔隙水压力分布云图

初始应力主要有自重应力及初始渗透压力，通过程序计算可得到x和y方向初始位移分布云图如图12所示。

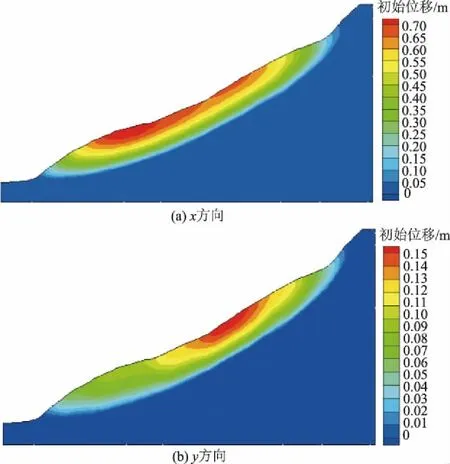
图12 x和y方向滑坡初始位移

4.5 计算结果

计算时为了使得非饱和渗流计算与蠕变计算同步，时间步长取为1 d，为了分析不同时刻渗流场，分别输出时间t为1,30，60,120，240，360 d时的孔隙水压力,如图13所示。

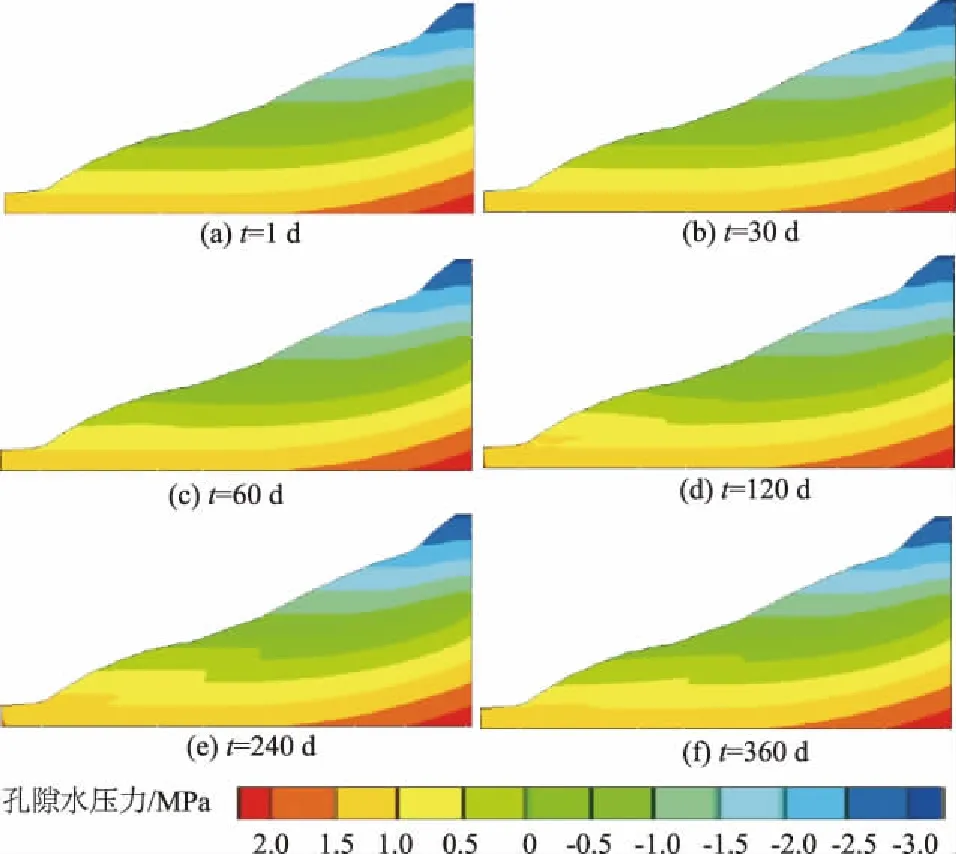
图13 不同时刻滑坡孔隙水压力分布云图

从图13可以看出，不同时刻的渗流场变化主要集中于库水位在145～175 m之间，而其他部位变化不是特别大，主要是因为库水位主要在145～175 m之间波动，对滑体上部影响较为有限。

图14 不同时间滑坡位移云图

图14给出时间t分别为30，60，120，240，360 d时x和y方向滑坡位移分布云图。

从图14可以看出，滑坡的变形主要集中在滑体部位，随着时间的推移，x和y方向的位移都逐渐增大，x方向最大位移从初始时刻的0.7 m左右增大至1.2 m左右，y方向位移从初始时刻的0.15 m左右增大至0.35 m左右。

为了验证计算结果，选取主滑截面上具有监测资料的点，将变形计算结果与实际监测资料进行趋势对比(为便于对比，变形都选取净变形，即实际变形与初始时刻变形的差)，如图15所示。

图15 变形计算结果与实际监测结果趋势对比

从图15可以看出，监测值出现一些波动，而计算值比较平滑，是因为监测采用的是多点位移伸缩计，所测得数据在局部存在一定波动误差。计算结果与实际变形的监测值尽管在数值的绝对大小上存在一定差异，但是变形趋势比较接近，即1 a时间里，变形逐渐增大，且随着库水位的升降划分为3个阶段：①随着库水位的上升，变形逐渐增大；②库水位保持在175 m左右时，蠕变变形逐渐进入衰减阶段；③库水位下降时，蠕变变形又逐渐增大，且蠕变增大幅度要比上升时大。这个过程相对于库水位的变动存在一定的滞后性，这可能是因为库水位的迅速升降过程中，滑坡体内渗流场改变存在滞后性。

5 结 论

(1)本文研究了改进后蠕变模型的参数求取方法，求解出了模型的所有参数，对试验数据进行模拟，并采用另一组数据对模型进行修正，结果表明：修正后的模型合理有效，能较好地描述该非饱和滑带土的蠕变趋势和主要特征。

(2)在对非饱和蠕变模型进行有限元数值分析时，需要同时计算非饱和渗流过程。根据蠕变模型与非饱和渗流方程的相对独立性及两者都与时间相关性，确定了在各个时步将非饱和蠕变模型和非饱和渗流方程分开求解的求解策略，并用一个实际算例进行计算分析，将计算结果与实际监测结果进行对比。结果表明：计算结果与实际变形的监测值趋势比较接近，本文所建立的蠕变模型合理，编制的程序可靠，可用于实际滑坡的长期变形计算。

滑坡土体变形是渗流与蠕变共同作用的结果，渗流产生的渗透力将会影响到土体蠕变特性，土体蠕变使得孔隙发生变化亦将影响到土体渗流，下一步将重点研究蠕变与渗流的耦合作用。