速凝浆液岩体倾斜裂隙注浆扩散模型研究

(1.长江科学院 水利部岩土力学与工程重点实验室，武汉 430010； 2.武汉市政工程设计研究院有限责任公司，武汉 430023； 3.长江科学院 武汉长江科创科技发展有限公司，武汉 430010)

1 研究背景

注浆法作为加固软弱围岩及封堵地下水的有效手段，在地下工程软弱岩土体的灾害治理中得到了较快的发展，其中水泥-水玻璃速凝类浆液最为常见[1-2]。在注浆过程中，浆液扩散半径、注浆压力与注浆速率等参数与工程设计、施工密切相关，其对工程灾害治理效果影响较大。近年来，根据注浆施工中遇到的不同岩土介质条件，许多新型注浆材料和设备相继研发并投入使用，取得了良好的效果，然而注浆理论的发展却较为缓慢，从而造成注浆工程存在一定的盲目性和不确定性，注浆技术缺乏科学、合理的理论指导。

目前，国内外许多学者在岩土介质中的浆液扩散运移规律方面开展了大量的研究。现有的注浆理论依据本构方程的不同，可分为牛顿流体、宾汉流体、幂律流体等[3-5]；依据浆液运动方程可分为渗透注浆、压密注浆、劈裂注浆、动水注浆[6-9]等。此外，针对注浆过程中常用的速凝类双液浆具有凝胶时间短、浆液扩散规律受时间和空间影响较大的特点，阮文军[9-10]基于试验和理论推导，构建了基于浆液黏度时变性的裂隙岩体注浆扩散模型；刘健等[11]基于毛细管渗透理论推导了考虑浆液黏度时变性的浆液扩散公式，以及注浆作用在管片上的压力理论解；李术才等[12]测定了水泥-水玻璃浆液的表观黏度时变函数，并推导了速凝浆液的单一平板裂隙注浆压力空间分布方程；张庆松等[13]综合考虑了浆液黏度时变性和空间分布不均匀性特征，建立了恒定注浆速率下考虑浆液黏度时空变化的水平裂隙注浆扩散模型；张军贤[14]基于平板裂缝假设，推导出幂律型流体劈裂注浆最大扩散半径公式，并通过现场注浆试验进行验证；慕欣等[15]、陈喜坤等[16]基于剪切试验和三轴压缩试验，分别研究了砂细度模数及不同围压对壁后注浆浆液强度的影响特征。上述模型均以水平平板裂隙为前提，尚未考虑岩体倾斜裂隙面的浆液自重作用影响，且真实地下工程中，岩体裂隙产状常呈不规则空间分布，完全水平的裂隙几乎不存在。

为解决上述问题，本文选取较为常用的水泥-水玻璃作为注浆材料，采用流体力学理论及粗糙裂隙等效水力开度确定方法，同时考虑了浆液自重作用影响，建立恒定注浆速率条件下综合反映浆液黏度时空变化的倾斜裂隙注浆扩散模型，定量确定了注浆压力与注浆时间及浆液扩散距离的关系，并利用数值模拟对所建立的注浆扩散模型的合理性进行了论证。研究成果可为水泥-水玻璃浆液的工程应用提供参考。

2 岩体倾斜裂隙注浆扩散模型

2.1 粗糙裂隙的等效水力开度

裂隙岩体是自然界中的一种极其复杂的介质，从力学性质上可将其组成简化为完整岩块和不连续结构面。已有研究表明，与砂岩等孔隙介质不同，完整岩块主要由细小颗粒组成，其物质结构较为坚硬、致密，孔隙率很小，渗透性十分微弱，而岩体中裂隙的导水能力极强，是岩体的主要渗透通道，因此裂隙岩体的渗透系数比岩块的渗透系数大得多，相差104～107倍[17-18]。可见，裂隙岩体浆液扩散特性研究的本质就是研究浆液在裂隙中的扩散规律。

在实际注浆施工中，一个灌浆段往往存在多条可灌裂隙，为研究方便，本文仅考虑单裂隙注浆的情况，这也是分析多裂隙网格浆液扩散的基础。

岩体中的天然裂隙面粗糙不平，缝隙内存在胶结或充填情况，使得裂隙开度大小非定值，其对浆液运动会产生较大的影响。根据流体力学理论，对于一光滑、平直、无限延伸的两平行平板裂隙，不可压缩牛顿流体作层流运动时，可以用立方定律来描述流体的运动特征。基于此，本文引入“等效水力开度”这一概念，来代替立方定律中的裂隙开度。即，在既定的水力梯度和流动方式下，同一流体在粗糙裂隙内的体积流量与一平直光滑、裂隙开度为b的体积流量相等，则b可认为是该粗糙裂隙的等效水力开度[19]。对于粗糙裂隙，参照立方定律[18]，存在如下关系,即

(1)

式中：q为单位缝隙宽度内的体积流量；b为等效水力开度，可通过钻孔水力编录和压水试验等方法确定[20]；μ为流体黏度；p为流体压强；γ为流体重度；h为测压点与基准面的垂直距离。

2.2 柱坐标下的倾斜裂隙注浆扩散模型

基于上述研究，对于任一产状的粗糙裂隙，可将其简化为平直、光滑、无限延伸的平板裂隙，然后利用等效水力开度代入分析。考虑速凝类双液浆在两平直、光滑平板所组成的裂隙作径向辐射流动情况，不妨令裂隙的等效水力开度为b，倾角为α，r为浆液流动方向，r轴的坐标原点位于灌浆孔轴线上，z表示裂隙开度方向，z轴的原点取在缝隙的中心,θ为r轴的方位角，裂隙的最大倾斜方向为θ轴。建立柱坐标系(r,θ,z)下浆液在倾斜裂隙面内的扩散示意图(图1)。

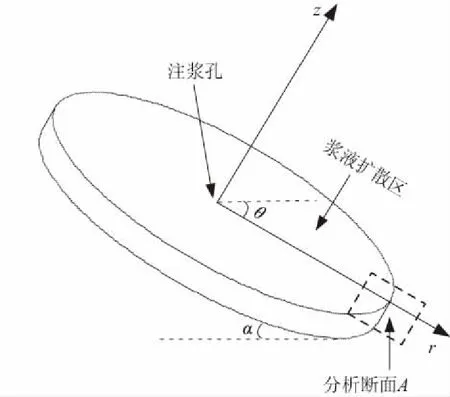
图1 倾斜裂隙中的浆液扩散示意图

3 速凝浆液倾斜裂隙注浆扩散模型

3.1 基本假设

为了推导速凝类浆液在岩体倾斜裂隙内的注浆扩散模型，基本假设如下：

(1) 浆液、水均为不可压缩的均质,是各向同性流体。

(2) 浆液为具有黏度时变性的宾汉流体，在注浆过程中浆液的配比和流型不变，且浆液进入裂隙后的流态为层流。

(3) 裂隙壁面无滑移边界条件成立，即壁面上的浆液流动速度为0。

(4) 浆液扩散方式为完全驱替扩散，不考虑浆水相界面处水对浆液的稀释作用。

(5) 浆液只在裂隙中扩散，忽略浆液渗透到裂隙两侧岩体所引起的浆液流失。

3.2 浆液本构方程

考虑到速凝类浆液具有黏度时变性，采用宾汉流体方程来描述浆液的本构方程,即

(2)

式中：τ为浆液的剪切应力；τ0为浆液的屈服剪切应力；μp(t)为浆液黏度时间函数；-du/dz为浆液剪切速率，u为浆液流动速度，z为空间距离。

3.3 浆液连续性方程

对于不可压缩黏性流体，运动连续性方程[21]为

(3)

式中：ur，uθ，uz分别为沿r轴、θ轴、z轴的流速分量。

浆液沿r轴运动，在z轴方向流速为0，则有：uz=0，uθ=0。可得：

(4)

3.4 浆液扩散运动方程

通过注浆孔取一垂直于裂隙的平面进行研究，以裂隙中心为对称轴，取浆液微元体进行受力分析，浆液流动受力示意见图2。图中，裂隙上下表面内为浆液，静水压力作用在浆液液面上。

图2 分析断面A下的浆液流动受力示意图

通过对流场中任一流体微元六面体进行受力分析，采用牛顿运动定律，可以得到惯性系中的黏性流体运动的动量方程，在柱坐标系中沿r轴方程为

(5)

式中：ρ为流体密度；p为流体在单位面积上的正应力；prr，prθ，pzr，pθθ的第一下标含义表示应力作用面的外法线方向，第二下标表示应力分量的方向；Fr为单位质量流体在r方向的重力分量。

根据本构方程(2),可以确定应力与流速间的关系：

(6)

式中p为流体压强。

将方程(3)、方程(5)代入方程(4)，忽略高阶小量，同时将pzr记为τ，ur记为u，可得

(7)

通过对单元体受力平衡微分方程进行分析，可得截面剪切应力和截面速度分布方程，如下：

(8)

由于宾汉流体的流动存在流核，流核高度在浆液流动过程中是随着压力梯度变化的。对于水泥-水玻璃双液浆，由于流体阻力大，一定注浆压力下的扩散范围要比水泥注浆的扩散范围小的多，因此不能忽略流核高度变化，流核的高度计为2zb。

(9)

对上述方程进行积分可得

(10)

(11)

忽略二阶项，可得

(12)

3.5 浆液扩散区内压力的时空分布

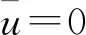
(13)

由于压力梯度dp/dr沿着r轴递减，则有

(14)

将p*=p-ρgrsinαcosθ代入上式，并从半径r0积分至rmax可得

(15)

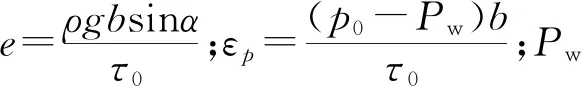
由方程(15)可知，浆液扩散轨迹为椭圆形，在不考虑浆液黏度影响下，其离心率e主要取决于浆液的密度、屈服剪切应力、裂隙面倾角和等效水力开度。

已有研究表明[8, 19-21]：单裂隙的等效水力开度要小于其平均开度(或力学开度)，当忽略岩体其它微裂隙时，其量值一般为0.1 mm级。此外，单液水泥浆的屈服剪切应力τ0一般较小，而水泥-水玻璃双液浆的屈服剪应力要大得多，椭圆离心率e一般<0.1，接近为圆形。因此，对于黏度随时间增长较快、扩散范围不大的速凝类浆液，为便于分析，可认为在静水压力条件下，浆液扩散轨迹的几何形态近似为圆形。理论分析和数值仿真均表明，该近似处理产生的误差是可接受的，可以满足工程需求。

在浆液流动过程中，依据质量守恒定律，可得:

(16)

(17)

对于t时刻，扩散距离rt为:

(18)

将p*=p-ρgrsinαcosθ代入式(17)可得，

(19)

将浆液从r处到t时刻位置进行积分，可得

根据速凝类浆液的黏度-时间特性，采用简化的黏度-时间函数进行拟合，即

μ(t)=AtB。

(21)

式中：μ(t)为流体黏度函数；t为时间；A，B为常数。

将式(21)代入式(20)，注浆压力-时间-空间分布关系，即p-r-t关系为

注浆压力-时间分布关系，即p-t关系为

(23)

注浆压力-空间分布关系，即p-r关系为

(24)

可见，当岩体裂隙面倾角α取0时，即为水平平板裂隙情况，退化后的方程(22)—方程(24) 与文献[13]的推导结果一致，表明本文构建的注浆扩散模型更具有一般性，可以求解任意空间产状裂隙的注浆时空扩散分布特征，而以往的水平平板裂隙扩散模型只是本文模型的一个特例。研究还表明，浆液性质、裂隙产状及参数、注浆参数及静水压力共同决定了速凝类浆液在岩体倾斜裂隙中的扩散特征，注浆压力主要取决于浆液黏度、屈服剪应力、裂隙产状、静水压力4个因素。

4 算例验证

为了验证理论结果的可靠性，本节构建了三维有限元分析模型，模拟浆液在裂隙内扩散过程中压力随时间和空间的分布特征。

4.1 模型的构建

有限元三维分析模型几何尺寸为2 m×2 m×0.005 m，注浆孔位于模型的几何中心。模型左、右边界为定压力边界，此边界压力为静水压力，进入裂隙的浆液与水均从该边界流出。模型上、下边界及两侧边界均为无流动边界，均满足无滑移边界条件。在初始时刻，模型内部充满了水，注浆开始后，浆液以恒定速率由注浆孔进入裂隙空间。模型网格采用自由三角形网格，靠近注浆孔处的网格适当加密，有限元模型网格划分及边界条件见图 3。

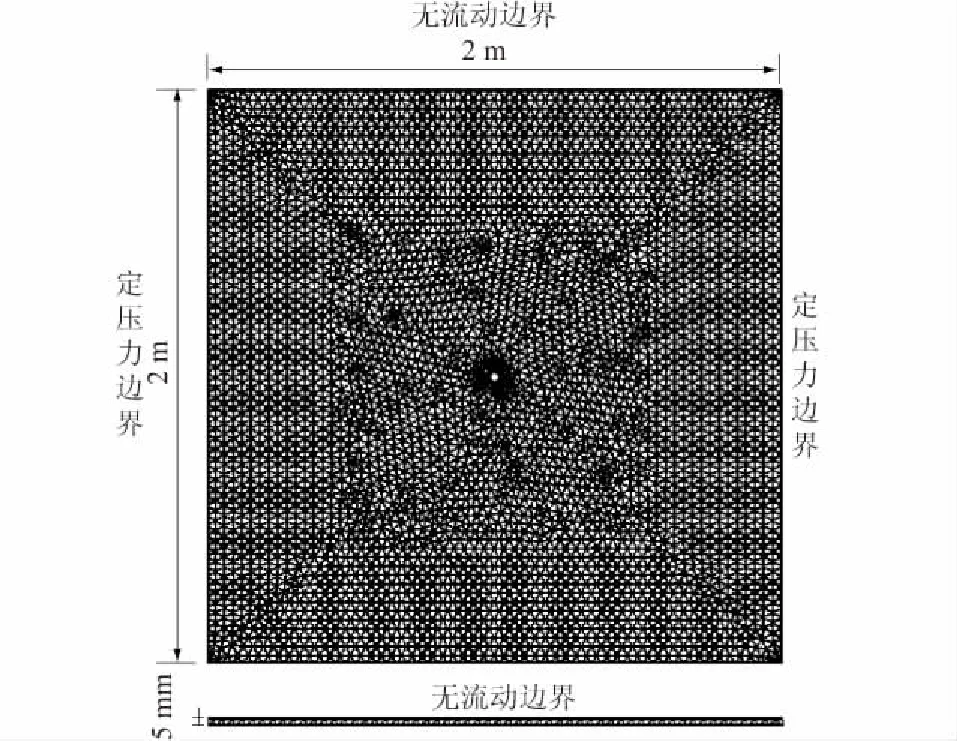
图3 网格剖分及边界条件

根据文献[13]试验结果，在反应时间0～70 s、反应温度20 ℃条件下，当水泥浆水灰比W∶C=1∶1、水泥-水玻璃体积比C∶S=1∶1时，C-S浆液的表观黏度-时间关系见式(25)，裂隙注浆参数见表1。

μ(t)=0.003 182t2.23+0.04 。

(25)

表1 裂隙注浆计算参数

将式(18)、式(25)联立求解，浆液黏度空间分布函数见式(26)，其空间分布特征见图4。

(26)

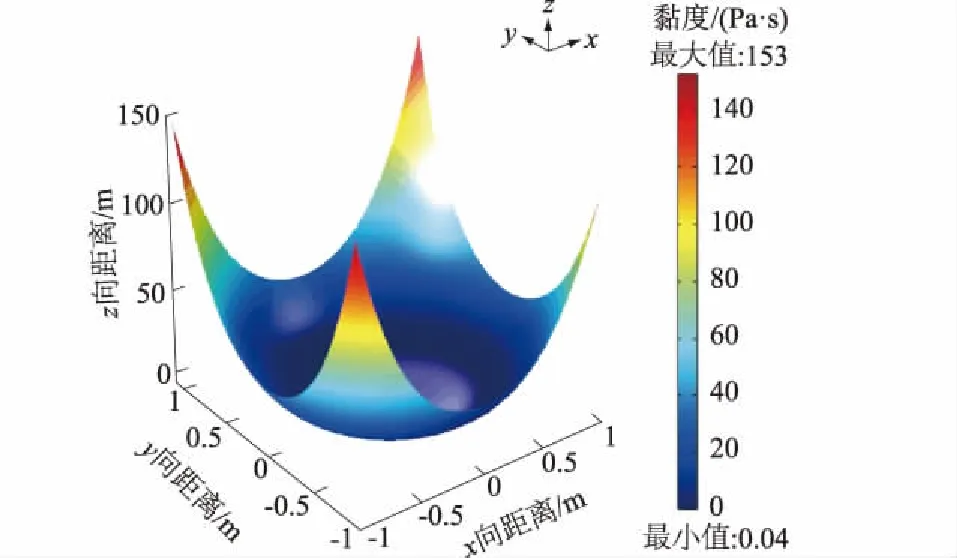
图4 浆液黏度空间分布特征

在浆水混合区域内，混合流体的平均黏度取决于浆液和水的黏度，以及二者所占的体积分数，本文浆水混合后的平均黏度计算如下：

(27)

式中：sg，sw分别为浆液和水的体积分数；μg，μw及μ分别对应浆液、水和浆水混合后的黏度。

4.2 控制方程

4.2.1 运动方程

流体运动方程采用Navier-Stokes方程，在三维条件下流体运动与受力的本构关系如下：

(28)

式中：ρ为流体密度;p为流体压强;t为时间;u为流体速度矢量;F为单位体积力;I为三阶单位矩阵;为哈密顿算子。

4.2.2 连续性方程

忽略浆液与水的压缩性，将浆液与水的密度视为常数。取裂隙空间内的特征单元体分析，由质量守恒定律得浆液和水各自流入和流出单元体的质量差应分别等于单元体内浆液和水的质量变化，得连续性方程为

(29)

4.3 计算结果对比分析

本节取裂隙倾角a=0°,30°，裂隙方位角θ=0°, 180°，综合采用理论和数值模拟方法，对比分析水平裂隙和倾斜裂隙下的注浆压力-时间分布特征。

4.3.1 注浆压力-时间分布规律

不同裂隙面倾角和方位角下的注浆压力-时间变化曲线对比情况见图5。

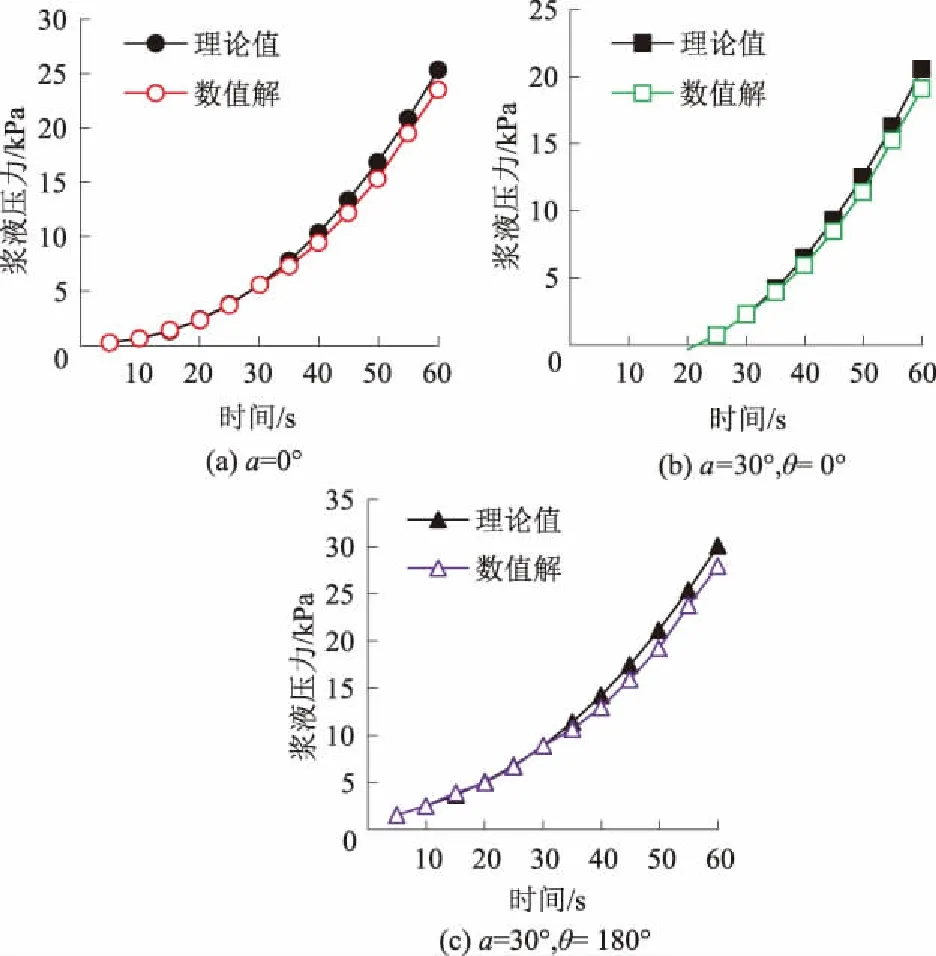
图5 注浆压力随时间的变化关系

对图5进行分析可知：

(1) 理论计算与数值模拟获得的注浆压力-时间变化规律基本一致，二者误差较小，误差均在8%以内，表明应用本文推导的理论公式能较好地描述浆液沿任意倾斜裂隙的注浆扩散过程。进一步分析可知，同一时刻下的注浆压力理论计算值略大于数值模拟结果，笔者认为，这是由于理论分析和数值模拟方法二者不尽一致引起的。理论分析中，假设浆液扩散方式为完全驱替扩散，不考虑浆水相界面处水对浆液的稀释作用，而在数值模拟过程中，综合考虑了水对浆液的稀释作用，浆水混合区的流体黏度要低于浆液黏度，从而导致数值模拟中浆液扩散的黏滞阻力要低于理论值，因此，理论计算获得的注浆压力要略大于数值模拟值。

(2) 注浆压力随时间变化呈现指数型增长规律，即随着注浆时间的持续，注浆压力逐渐增大，在注浆初期的注浆压力增长速率较小，而在注浆后期的注浆压力增长速率明显加快。

(3) 浆液扩散方位角和裂隙倾角均会对注浆压力随时间分布产生显著的影响。当浆液运动方向与裂隙面倾斜方向一致(图5(b))时，即浆液扩散方位角θ=0°，随着裂隙倾角的增大，在相同时间内的注浆压力较小，这是由于裂隙面倾斜时，浆液具有向下的自重分量，其与注浆压力一起克服浆液阻力，促使浆液向下运动，在恒速率注浆情况下，裂隙倾角越大，注浆压力越小；当浆液运动方向与裂隙面倾斜方向相反(图5(c))时，即θ= 180°，随着裂隙倾角增大，注浆压力相应就越大，增大的注浆压力用于克服浆液自重和黏滞阻力双重作用。

4.3.2 浆液压力-空间分布规律

分别取注浆时间t=35,55 s 进行分析，不同裂隙面倾角和方位角下的浆液压力-空间分布曲线对比情况见图 6。

图6 不同时刻浆液压力的空间分布曲线

对比分析理论计算与数值模拟结果可知：

(1)理论分析与数值模拟获得的浆液压力-空间衰减曲线变化趋势一致，但距离注浆孔相同位置处，不同时刻下的浆液压力数值模拟结果要小于理论分析值，这主要是由于数值模拟中考虑了水对浆液的稀释作用，从而导致浆水混合区内的黏滞阻力要低于理论值。此外，理论值和数值模拟结果二者误差较小，最大误差均在10%以内，表明本文所得的理论值与数值模拟结果吻合较好，进一步论证了理论公式的合理性和可靠性。

(2)浆液压力由注浆孔向四周衰减，随着远离注浆孔，浆液压力衰减速率逐渐增大。在注浆初期，浆液黏度较低，浆液压力衰减较为平缓；在注浆后期，浆液扩散锋面附近的浆液黏度远高于注浆孔附近的浆液黏度，导致浆液扩散锋面处的压力梯度远大于注浆孔附近的压力梯度，因此浆液压力衰减较快，呈现明显的非线性特征。

(3)浆液扩散方位角和裂隙倾角对浆液压力的空间分布特征产生显著影响。当浆液运动方向与裂隙面倾斜方向一致(图6(b))时，即浆液扩散方位角θ=0°，浆液压力随着注浆孔距的增大呈现先增大后减小的特征，随着裂隙倾角的增大，距注浆孔中心相同距离的压力较小，这主要是由于裂隙面倾斜时，浆液具有向下的自重分量，其与浆液压力一起克服浆液黏滞阻力，促使浆液向下运动，在恒速率注浆条件下，裂隙倾角越大，浆液自重分量越大，浆液压力相应就越小；当浆液运动方向与裂隙面倾斜方向相反(图6(c))时，即θ= 180°，浆液压力由注浆孔向四周衰减，注浆孔附近的浆液压力最大，随着裂隙倾角的增大，距注浆孔中心相同距离的浆液压力相应就越大，这主要是由于裂隙面倾斜时，浆液具有向下的自重分量，增大的浆液压力用于克服浆液自重分量和黏滞阻力双重作用。在注浆后期，由于浆液扩散锋面处的浆液黏度远高于注浆孔附近的黏度，导致浆液扩散锋面处的压力梯度远大于注浆孔附近值，此时，浆液自重作用影响较小。

综上所述，本文构建的理论公式和数值分析模型较好地描述了速凝类浆液沿倾斜裂隙的注浆扩散过程，因此，在实际注浆过程中，可依据上述理论成果，合理估算注浆工程设计参数(注浆终压、注浆速率与扩散半径等)，减少注浆参数确定的盲目性，进一步提高注浆效率。

5 结 论

(1)基于流体力学理论及黏度时变性宾汉流体本构方程，并引入粗糙裂隙等效水力开度的确定方法，建立了恒定注浆速率条件下考虑浆液黏度时空变化的倾斜裂隙注浆扩散模型，并推导了浆液扩散区内的黏度及压力时空分布方程。

(2)与以往常以水平平板裂隙为前提构建的注浆扩散模型相比，本文构建的模型不受裂隙面产状的影响，可以求解任意空间产状裂隙的浆液扩散分布特征，其结论具有一般性，即以往的模型只是本模型的一个特例。此外，引入的粗糙裂隙等效水力开度确定方法，进一步拓宽了本文模型的应用范围。

(3)通过将理论分析结果与数值模拟值进行对比可知，注浆压力-时间增长曲线、浆液压力-空间衰减曲线均吻合较好，表明应用本文推导的理论公式能较好地描述浆液沿任意倾斜裂隙的注浆扩散过程，进一步说明了理论公式的合理性和可靠性。研究成果可对注浆工程设计参数(注浆终压、注浆速率与扩散半径等)的确定提供依据。