喷雾机喷杆有限元模态分析与试验

乔白羽，丁素明，薛新宇，崔龙飞，顾 伟，陈 晨

(农业部南京农业机械化研究所，南京 210014)

0 引言

喷杆式喷雾机具有病虫害防治效率高、效果好、作业损害率低等优点，近年来已经逐渐发展成为大田作业中应用最广泛的植保机型[1]。然而，现阶段我国保有的喷杆式喷雾机整机质量一般小于1 500kg，满载药量1 000L以内，作业喷幅多在12m左右，导致喷雾机的实际喷洒效率低[2-3]。在田间作业过程中，由于该类中小型喷杆式喷雾机一般未配备喷杆悬架减振系统且动力学性能较差，喷杆结构与机身多采用直接连接的方式，作业行驶路面不平度对喷雾机机身产生的外部激励会直接传递给喷杆结构，引起喷杆结构振动，导致药液重喷漏喷率升高，影响喷雾的分布均匀性[4-7]。因此，需要通过分析现有大型喷杆喷雾机喷杆结构的动力学特性，研制出振动小、动力学特性良好的喷杆，从而提高喷杆喷雾机的喷雾均匀性和作业效率，为后续大型喷雾机田间作业的高效性提供依据。

为了减轻喷杆的振动、提高喷杆在田间作业过程中的稳定性及喷杆的动力学特性，国内外学者都进行了相关的研究。Langenakens J[8]等人研究了喷雾机喷杆结构的模态信息，利用数值求解法获得喷杆仿真模型的模态信息，并验证了模型的真实性，为喷杆的模态分析和拓扑结构优化奠定基础。Nation H. J.[9]等研究了喷杆回转连接机构对喷杆振动特性的影响，结果表明：为了减轻喷杆的振动，应该避免在回转关节采用钢索、弹簧等柔性连接，为喷杆的抑振性能及回转关节的研究提供可行性思路。陈晨[10]等人研究了单段式喷杆的动力学特性及结构优化，为多段式喷杆的动力学性能研究及结构优化做准备。张际先[11]等仿真喷雾机机身随路面起伏以不同频率作用时喷杆的振动情况，为喷杆的振动变形及随机路面谱响应分析提供依据。何耀杰等[12]结合喷杆的模态信息研究了在不同位置添加拉索后对喷杆振动特性的影响，结果表明：在喷杆3/4位置处安装拉索可以有效抑制喷杆的弹性变形。本文以某五段式喷雾机喷杆作为研究对象，对该喷雾机的整机喷杆进行有限元分析及模态试验验证，并将理论分析结果与试验模态分析结果进行对比，验证了理论分析的准确性。该验证结果可为后续喷杆的结构优化提供理论依据，对喷杆的轻量化设计具有一定的意义。

1 喷杆的基本参数以及三维建模

此次研究的喷杆主要是由方形钢管和圆柱形钢管焊接而成的五段式喷杆，整个喷杆总长为12m，机架两侧分别为含有转动关节的两段式喷杆，如图1所示。将机架右侧远离机架的喷杆作为末端喷杆，靠近机架的喷杆作为首段喷杆，末端喷杆与首段喷杆以回转关节的方式折叠放置，首段喷杆与机架直接相连，是振动传递的主要来源。整个机身主要包括4根方形钢管、6根圆柱形钢管、药箱、连接部件及其他辅助构件。

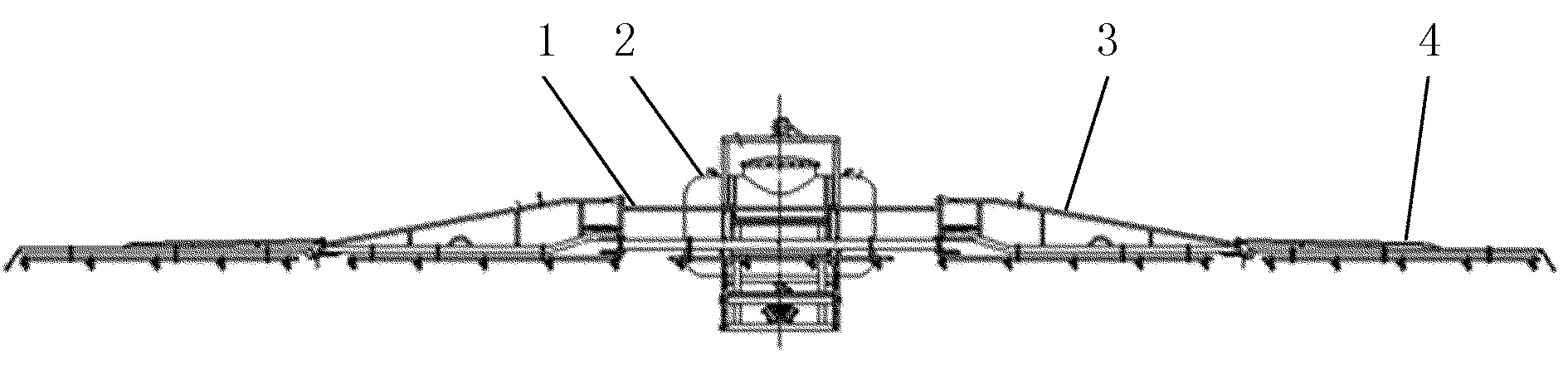
1.机架 2.药箱 3.首段喷杆 4.末段喷杆

2 有限元模型的建立

2.1 有限元模态分析理论介绍

由于机械结构在受到动载荷作用时结构自身发生振动，导致结构产生共振或者材料疲劳，从而对结构造成损坏，所以需要了解机械结构自身的振动特性。固有频率和模态阵型是结构振动特性的两个重要参数，其属性直接关系到机械结构工作的安全性和使用寿命[13]。

本次模态分析的主要目的是研究喷杆的振动特性，即喷杆结构的固有频率和振型，从而避免喷杆喷雾机在作业过程中由于振动而发生事故。所以，在进行结构设计时，模态分析是不可或缺的组成部分。其结果不仅能够说明喷杆结构的刚度情况，还可以为接下来的动力学分析与振动故障诊断打下基础[14]。模态分析作为最基本的动力学分析，是其他动力学分析的基础，如随机振动分析、谐响应分析及响应谱分析等都是在模态分析的基础上进行的[15]。

结构振动的一般微分方程为

(1)

式中M—振动系统的质量矩阵；

C—阻尼矩阵；

K—刚度矩阵；

F—系统所受的外部激励；

x—结构振动的位移向量[16]。

本次采用的是无阻尼线性结构分析。无阻尼线性结构自由振动的控制方程为

(2)

假设结构的运动是简谐运动，则

{x}={φ}isin(ωit+θi)

(3)

(4)

将结构运动的位移和速度带入到控制方程中，可以得到

([K]-ω2[M]){φ}i={0}

(5)

要满足上述方程，有两种情况：

1){φ}i=0。这种情况表明结构自身没有振动，但是实际情况结构不可能没有振动，所以舍去这种情况。

2)det([K]-ω2[M])={0}。这是一个特征值问题，可以求解出n个方程的根(ω12,ω22,...,ωn2)。这些根是此方程的特征值，每一个根(特征值)都对应着一个特征向量({φ}1，{φ}2，...,{φ}n)。在模态计算中，特征值等于结构固有频率值的平方；特征向量对应于结构的阵型，也就是结构的每个固有频率都关联1个模态形状向量[17]。

事实上，喷杆具有多个固有频率和模态振型，在设计结构时应该避免各阶固有频率和可能的振源振动频率接近。在工程应用中，低阶的模态对喷杆的动态特性影响比较大。由于低频振动的波长比较长，因此喷杆的低阶阵型对整个喷雾机的减振和稳定性具有重要作用。

2.2 模型的建立

2.2.1 模型的导入

Pro/E是机械设计广泛应用的三维建模软件，具有强大的三维实体建模功能，在对喷杆结构进行三维建模时通常是通过软件的拉伸、旋转和切割等命令来完成的[18]。因此，为便于分析，在进行模态计算之前需要对喷雾机喷杆的三维模型进行必要的简化，以提高模态分析的运算速度。具体包括：①不考虑焊接对喷雾机喷杆振动特性的影响；②所有的工艺孔都忽略不计，不考虑它对喷杆模态分析的影响；③所有的倒角和过渡圆角都简化成直角；④忽略不重要区域的小尺寸区域。在此基础上，对喷杆进行模态分析[19]。

2.2.2 网格划分

在进行模态分析时，有限元网格划分是非常重要的一步。网格划分的好坏会直接影响到计算结果，网格划分太密不利于提高计算精度和计算速度，网格划分太疏也不利于计算精度[20]。因此，在划分网格时需要采用合理的方式，此次采用自由网格划分的方式进行网格划分。运用三维建模软件建立机架的实体模型后，将机架以“.x_t”格式导入到ANSYS Workbench中，设置单元格大小为20mm，在对喷杆整体进行模态分析之后，最终得到的有限元模型如图2所示。

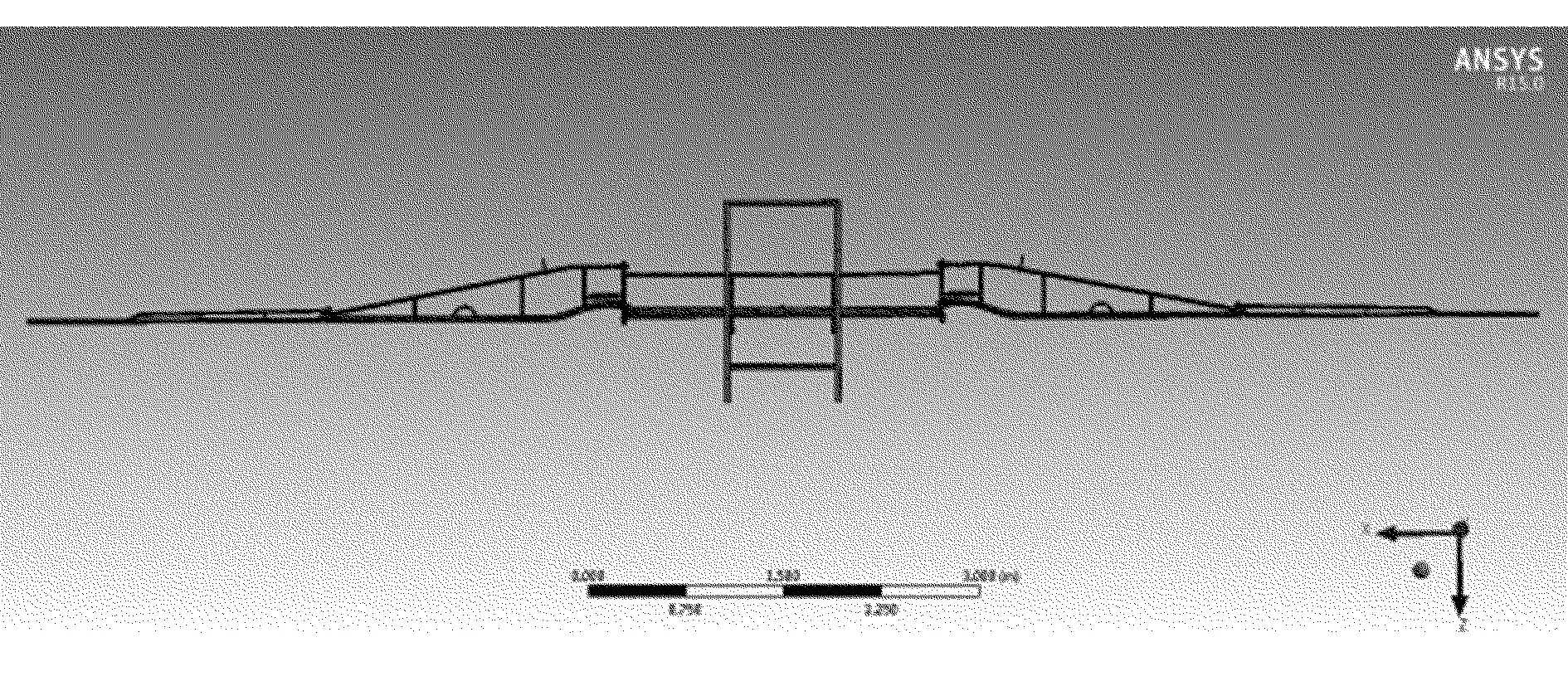
图2 喷杆有限元模型Fig.2 Finite element model of the spray boom

其中，网格节点数是122 584个，网格单元数为50 502个。

2.2.3 材料属性和边界条件

由于此次有限元模型建立采用自由网格划分的方式，所以只考虑喷杆自重的影响。机架的材料是Q235结构钢，弹性模量为207GPa，泊松比是0.3，质量密度是7.8×103kg/m3，如表1所示。

表1 材料属性参数表Table 1 Material property parameters

3 数值模态分析

喷杆喷雾机喷杆的模态分析的目的主要是得到喷杆的固有振动频率、相应阶数的振动动画及阵型云图等。由于喷杆喷雾机的轮胎具有低通滤波性，因此底盘在田间作业时受到的激励频率一般都小于10Hz[21-23]；而当喷雾机在田间作业时，凹凸不平路面对底盘的激励力会直接传递给喷杆，导致喷杆的固有频率低于10Hz时会与底盘发生共振，导致喷杆产生较大的变形。

表2为喷雾机喷杆结构在自由模态分析下前8阶的固有振动频率，喷杆的前6阶固有频率均在10Hz以下，所以喷杆在田间作业时容易发生共振，导致喷雾不均匀，作业效率降低。图3为喷杆前8阶的模态阵型云图。

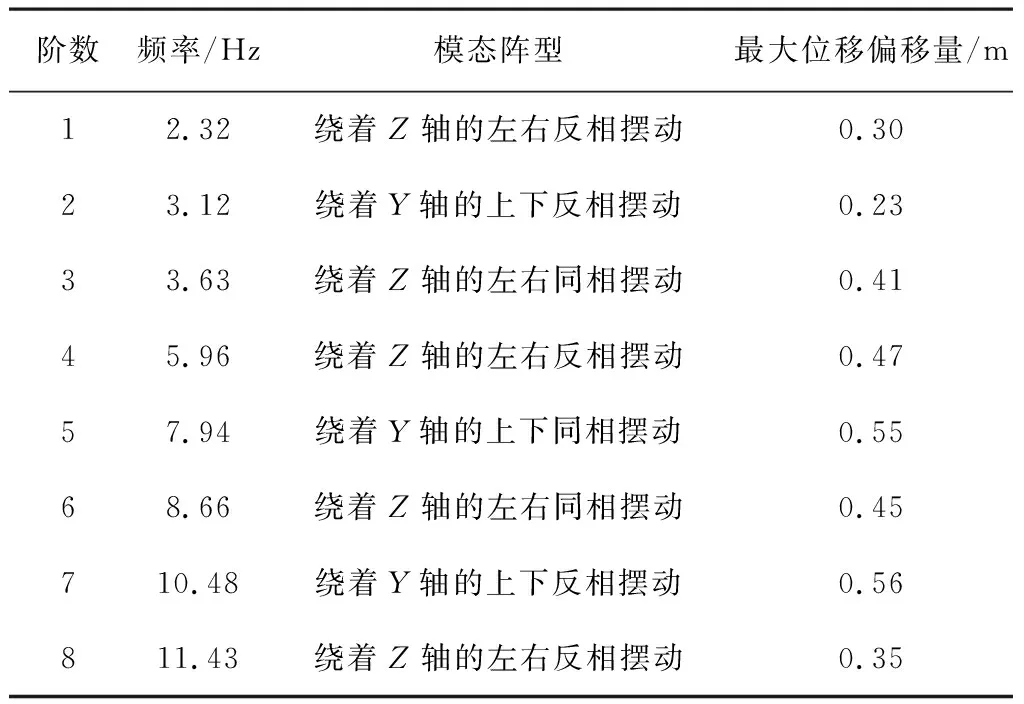
表2 喷杆前8阶各阶模态的固有频率Table 2 The natural frequency of first 8 modes

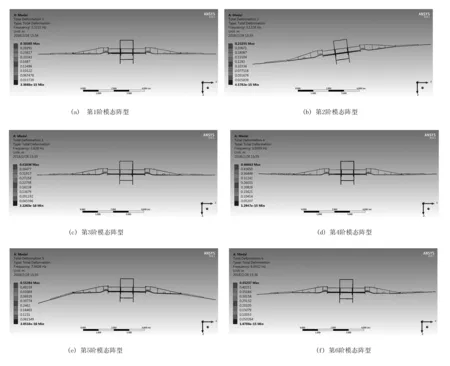
图3 前8阶模态阵型云图Fig.3 The first 8 modal shapes

4 试验模态分析

对喷杆进行模态分析后，需要通过模态试验来验证模态分析的计算结果。模态试验是基于外界激励和系统响应的动态测试，是利用系统输入的激振力和输出的响应数据，结合信号处理和参数识别来确定系统的模态参数。这种方法能够获得结构振动的固有特性，所以也是判断有限元模型准确性的重要目标[24-26]。

4.1 试验设备

本次试验仪器包括ICP加速度传感器、YTRAN激振力锤、VibPilot-8数据采集仪及SO Analyzer动态信号分析系统。在模态试验的过程中，使用激振力锤敲击喷杆结构给出激振信号，用加速度传感器来采集振动响应输出信号，然后利用动态信号分析系统对采集到的输入激励信号及输出响应信号进行处理得到频响函数，再利用数据采集分析软件进行进一步分析获取多段式喷杆结构的模态参数。具体所用仪器如图4～图6所示。

图4 模态试验现场Fig.4 Modal test

图5 加速度传感器Fig.5 Acceleration sensor

图6 激振力锤Fig.6 Exciting force hammer

4.2 测点位置分布

各个节点的位置坐标值如表3所示。

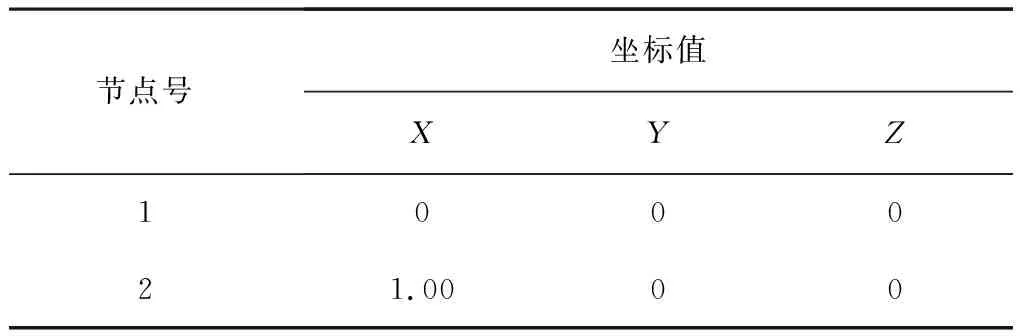
表3 各激振点位置坐标值Table 3 Coordinate values of exciting point positions

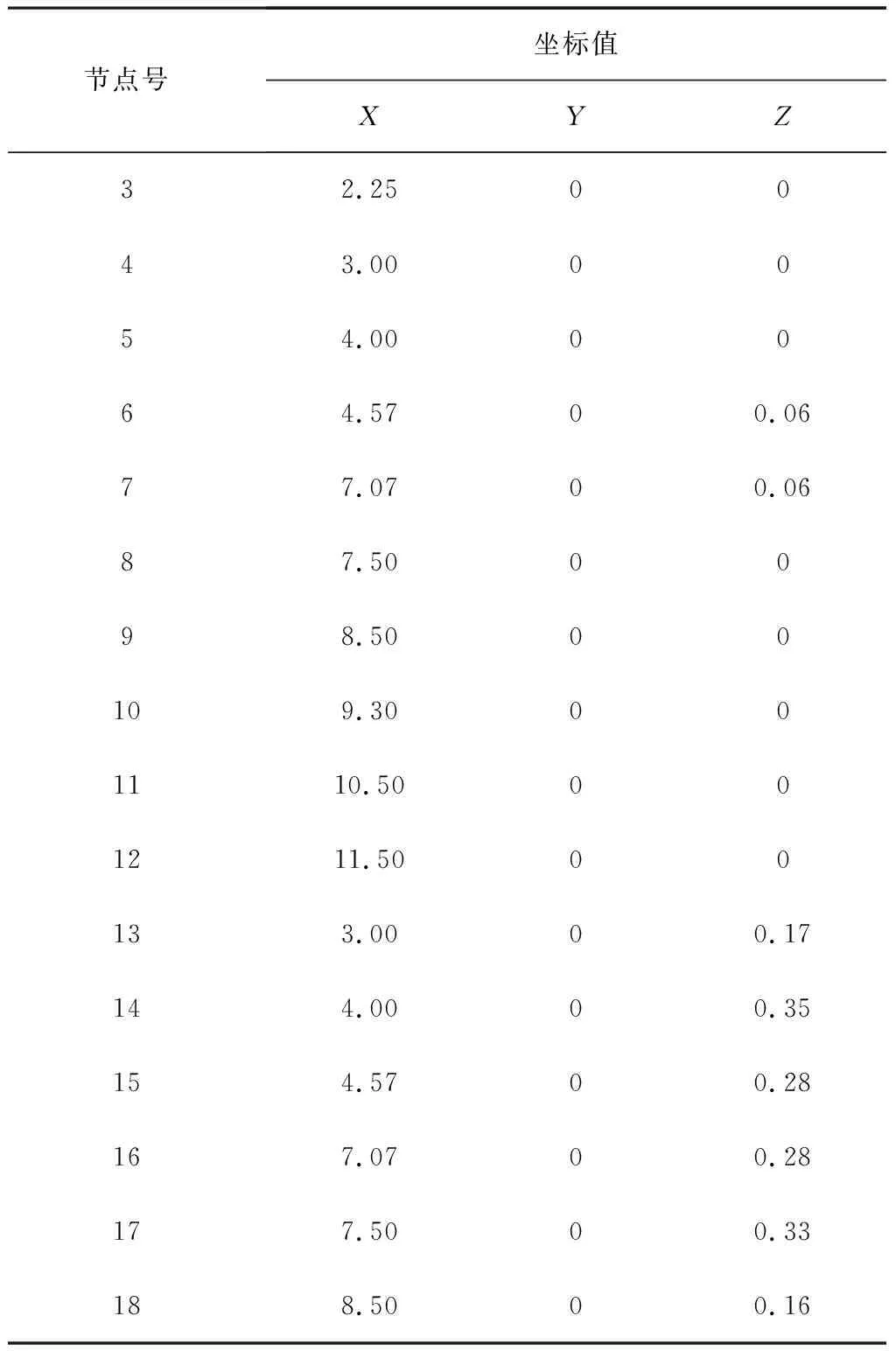
续表3

定义水平向右作为X轴的正方向，竖直向上作为Z轴的正方向，垂直向里作为Y轴的正方向。本次研究的喷杆总质量为100.8kg，总长为11.5m，呈现左右对称的结构分布。所以，首先对该喷杆进行节点划分，以确定传感器的位置。在左右两侧的喷杆上各划分6个点，并在底端喷杆的上侧两侧杆上各划分3个点，一共18个点，作为传感器的粘贴位置。

4.3 锤击测试

本次试验采用锤击法，即使用激振力锤敲击多段式喷杆，迫使喷杆产生强迫振动，然后对强迫振动产生的测量数据进行处理。试验的具体过程为：用行车牵引，弹簧与喷杆呈三角悬挂，利用弹簧可以保证此次试验与数值模态分析具有相同的自由边界条件。本次试验采用固定传感器的位置、移动力锤的方法进行。首先，将加速度传感器用胶水粘贴在已经编号的喷杆位置上；随后，对SO Analyzer动态分析软件进行设置；设置结束后，开始试验。用力锤依次敲击编号为1～18的节点，每次敲击进行3次，最后得到多段式喷杆水平方向和竖直方向的频响特性曲线和时域特性曲线(见图7～图9)；随后，进入Mode Model Validation模块，进行模态模型的校验并对模态参与因子进行计算。

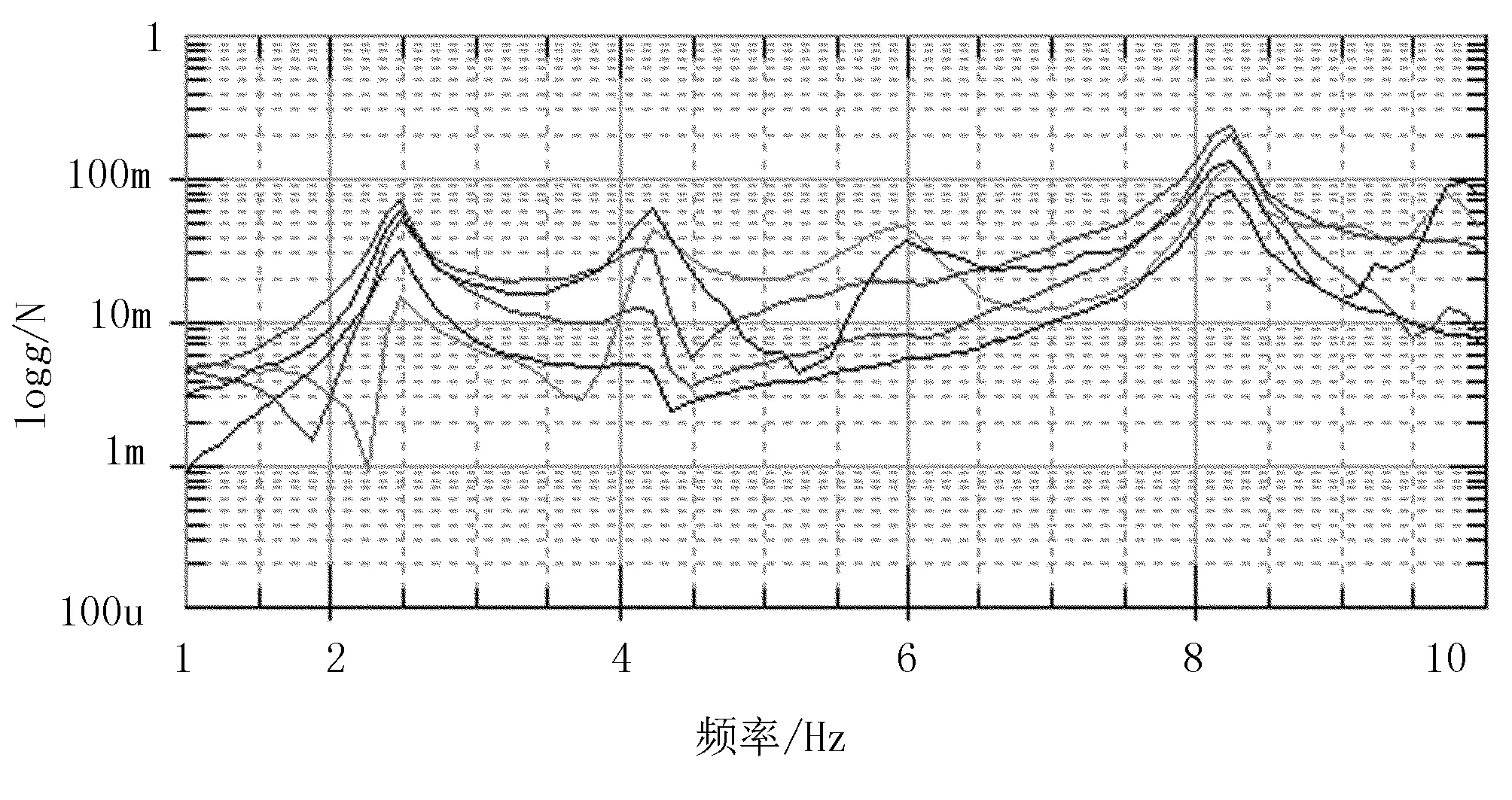
图7 各响应点水平方向的频响曲线Fig.7 Horizontal frequency response curve

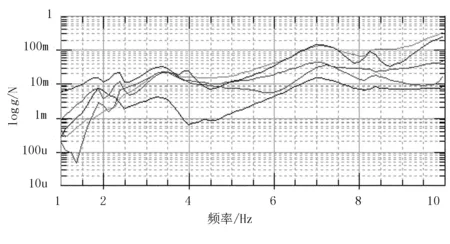
图8 各响应点竖直方向的频响曲线Fig.8 Vertical frequency response curve

图9 时域曲线图Fig.9 The time domain characteristic curve

喷杆的试验模态与解析模态的频率差如表4所示。

表4 试验模态与解析模态的频率差Table 4 Modal frequency difference between experimental and analytical modes

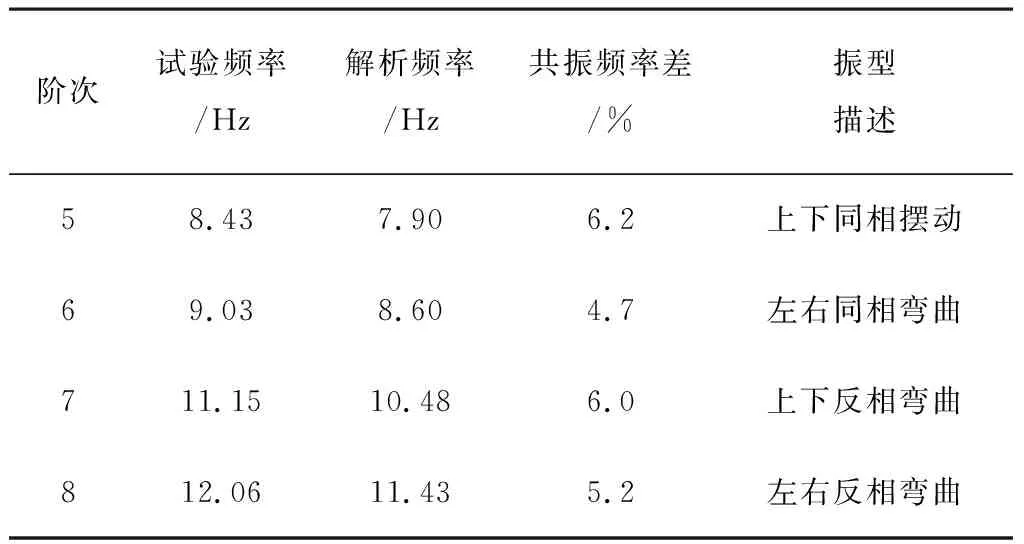
续表4

水平和竖直的频响特性曲线图中各条曲线分别代表各个响应点的频响函数输出值，也就是输出响应与输入响应之间的关系。从图中可以看出：各个响应点的频率响应保持一致，同各阶的理论模态值相接近，证明了试验的合理性。时域曲线表示的是各个响应点时域函数输出值的实部，从图中可以看出喷杆振动的衰减特性，8s以后基本衰减完成。

4.4 试验结果

分析比较结果可以得到：试验模态和解析模态的前8阶振型的共振频率差均小于10%，同时各阶振型所对应的模态置信准则都大于0.8，因此可以推断出上述所建立多段式喷杆的有限元模型是合理的。模态置信准则表MAC图如图10所示。

图10 模态置信准则Fig.10 Modal confidence criterion table MAC

本次试验得到的模态结果振型协调，采用不同的试验方式多次试验结果互相吻合，MAC矩阵仅对角线值为1，其余值接近于0，表明各阶模态结果互相正交，结果可以信赖。

5 结论

1)通过对喷雾机喷杆结构进行三维建模及数值模态计算，得到了其前8阶固有频率和阵型云图，确定了喷杆的前6阶固有频率均在10Hz以下，为后续进行的谐响应分析及瞬态响应分析等结构动力学性能优化设计奠定了基础。

2)通过对比数值模态分析与试验模态分析结果可以看到：数值分析结果存在一定的误差，但共振频率差均小于10%，各阶振型所对应的模态置信准则都大于0.8，误差在允许范围内。由此验证了理论分析的可靠性。

3)通过对喷杆有限元模态分析得到的有效结果，可以为实现喷杆的防振减振、避开不良的固有频率及实现喷杆的结构改造提供准确的理论依据。