基于熵值组合模型的矿业复垦土壤重金属高光谱反演

夏 可，张世文，沈 强，杨邵文，夏沙沙，胡青青

(1. 安徽理工大学 测绘学院，安徽 淮南 232001； 2． 安徽理工大学 地球与环境学院，安徽 淮南 232001)

1 引 言

中国作为世界人口大国之一，同时也是一个能源消耗大国。据相关资料显示，目前我国矿山约有103 187个，大中型矿山9 399个，小型矿山和个体矿93 788个。我国矿产资源丰富，许多矿山已有近百年的开采历史，为我国的经济建设和地区发展做出了极大的贡献，与此同时，随着矿产资源的开采，对矿山周边的环境造成了严重的污染和破坏。习近平总书记在党的十九大报告中指出，坚持人与自然和谐共生，树立金山银山就是绿水青山的理念，因此矿山生态修复以及土地复垦显得愈发重要。截至2017年底，我国新增矿山恢复面积约4.43万hm2，治理下的矿山约10 032个[1]。

土地复垦与生态修复是治理矿山的有力手段，矿区土地与环境监测则是土地复垦与生态修复的前提和基本要求。在矿山开采过程中造成的矿业废弃地污染以重金属为主，重金属污染对人体造成的危害巨大，因此土地复垦中对重金属的检测尤为重要。重金属检测可以为土地复垦提供方案选择、复垦效果评价，实现长期动态监测。传统的重金属检测以实验室测定为主，例如原子荧光法(AFS)、电感耦合等离子体法(ICP)、电感耦合等离子质谱法(ICP-MS)、原子吸收法(AAS)等，其效率低、成本高，无法实现大面积检测，且长期动态监测比较困难。近年来，高光谱遥感技术以其独特的优势，在很多领域研究中得到了良好的发展与应用，这也为土壤重金属检测提供了一个全新的途径。国内外众多专家与学者利用高光谱遥感对土壤中各成分都进行过大量的研究，王维等发现一阶微分高光谱反演模型对土壤重金属Cu具有较好的估算潜力[2]；Srivastava等利用偏最小二乘回归模型对印度旁遮普印度恒河平原的土壤有机碳含量进行了快速的预测[3]；Babaeian等利用不同光谱分辨率下的光谱特征提取土壤水力参数，并用HYPRES和Rosetta pedotransfer函数进行评价，结果表明估计的性能取决于水力参数的类型以及输入信号的频谱分辨率[4]；沈强等通过一阶微分、倒数对数、连续统去除法结合多元逐步回归模型，发现矿业废弃地重构土壤中As的最佳反演模型为连续统去除法逐步回归模型[5]；李晋华等通过多光谱数据进行多元散射校正预处理，并结合偏最小二乘模型对玉米成分进行预测，取得了较好的效果[6]；李旭青等利用光谱数据对水稻冠层氮素含量建立反演模型，结果表明随机森林算法可有效地对水稻冠层氮素含量进行解释、且所需样本少、不易拟合[7]。

前人在土壤成分含量估测方面做了大量的研究并取得了较好的结果，但多集中在单一预测模型，单一预测模型往往不能全面反映事物的信息，信息的缺失又将会导致预测的偏差[8]，因此为了减弱单一预测模型中随机因素的影响，提高模型预测精度，本文以四川省古蔺县石屏硫厂废弃地复垦土壤为研究对象，基于Matlab和Python编程平台以多种光谱数据预处理结合线性模型与非线性模型进行对比，在此基础上寻求较优单一模型，探讨较优模型组合方式在土壤重金属含量高光谱估算中应用的可行性，以期为基于高光谱遥感技术下的矿业废弃地复垦土壤重金属快速检测提供理论和方法支持。

2 实 验

2.1 研究区概况

研究区位于四川省古蔺县石屏乡(东经105°59′54″～106°01′57″，北纬28°01′3″～28°02′51″之间)，地处四川盆地与贵州高原的过渡地带，具有四川盆地气候和高原气候特征，四季分明、雨热同期，年降水量偏少，温度适中，光照条件较充足，年平均气温在13.8～18.6 ℃之间。研究区总面积约为4 451.89亩，从上世纪50年代始建，主要从事硫磺开采和冶炼，随着时间的推移，矿区废弃物堆积如山，对周边土壤和环境造成严重破坏。研究区于2013年进行复垦，复垦方向主要为林地、耕地和草地，复垦措施主要为覆土、平整和土壤改良，并于2014年底完成复垦。

2.2 数据获取

数据主要来源于实验室测定和光谱测量。在研究区内采用网格随机布点，共采集65个土壤样本，土壤采样深度为0～20 cm，主要涉及的复垦地块类型有矿渣堆、旱地、林地、水田。将采集的土样经自然风干、研磨、过100目筛，各取100 g，分成两份，一份用于实验室测定土壤重金属含量，一份用于光谱测量。实验室土壤重金属的测定采用电感耦合等离子法，光谱数据利用美国ASD(Analytical Spectral Devices)公司生产的Fieldspec 4便携式地物光谱仪测定。在进行光谱测量时，选择光线较暗的实验室，提前预热机器10 min，调整好探头与光源位置，将样本放在培养皿中，下面用黑布平铺，实验之前进行白板校正，实验过程中每10个样本进行一次白板校正。每个样本测定10次，取其平均值作为最终的光谱数据，利用RS3软件进行光谱数据收集，ViewSpecPro软件进行数据后处理。利用K-S(Kennard-Stone)算法划分建模样本和验证样本，K-S算法能够根据光谱变量间的欧式距离，在特征空间中均匀地选取光谱差异较大的样本[9]，较传统随机选样或根据距离和含量选样更为合理。

2.3 数据预处理

光谱测量过程中由于仪器的原因、人为因素的影响以及外界环境的干扰都会对光谱数据造成影响。而这些噪声对特征波段的选取和模型的建立都会造成影响，为此我们首先对光谱数据进行S-G平滑处理以减弱噪声[10]，其次再对数据进行一阶微分[11](First order differential，FDR,公式(1))、离差标准化[12](Deviation standardization, DS,公式(2))、多元散射校正[13-14](Multiplicative scatter correction,MSC,公式(3)～(5))和连续统去除法[15-16](Continuum removal,CR)等预处理变换。

(1)

(2)

其中，λi为第i个光谱波长，R(λi)为对应光谱波长的反射率，Δλ为λi+1与λi之间的差值，R(λmax)、R(λmin)分别为某一样本的最大反射率和最小反射率。

(3)

(4)

(5)

2.4 建模方法

2.4.1 偏最小二乘

偏最小二乘(Partial least squares，PLS)的基本原理是通过最小误差的平方和找寻一组数据的最佳匹配函数，它是传统的多元线性回归、典型相关分析和主成分分析的集合体[17-18]。较传统多元线性回归而言，偏最小二乘能够允许自变量直接存在多重相关性，可以在样点个数低于变量个数的情况下实行建模。建模原理为：建立m×n的光谱矩阵X，n×l的重金属含量检测矩阵Y，其中m为光谱波段数，n为样品个数，l为重金属种类。

将X、Y进行分解，公式如下：

X=TPT+E，

(6)

Y=UQT+F，

(7)

其中，U、T为得分矩阵，P、Q为载荷，E、F为PLSR模拟时的残差矩阵。对U、T做线性回归，B为关联系数矩阵，有U=TB，重金属含量预测公式为：

Y预测=T计算BQ=X测量PTBQ.

(8)

2.4.2 人工神经网络

人工神经网络(Artificial neural network，ANN)是一种仿生物神经网络技术，由大量神经元连接而成，主要分为输入层、隐藏层和输出层。人工神经网络具有自适应和自主学习的能力，因而在处理大量随机性数据和非线性数据方面具有明显优势[19]。

2.4.3 随机森林

随机森林(Random forest，RF)算法最早由Leo Breiman和Adele Cutler所提出，能够处理高维特征且不易产生过拟合，对于大数据而言，模型训练速度较快，对数据的适用能力较强[20-21]。基本原理为：设训练样本个数为M，特征数目为N，从M个训练集中以bootstrap取样方式取样M次，对未抽取样本进行预测和评估误差，针对每一节点随机选取n个特征，根据这n个特征选择最佳分裂方式，其次在每个训练子集上构建决策树，最后根据每棵决策树的输出取平均或投票作为最终结果。

2.5 熵值权系数组合模型

组合模型是将多个模型综合在一起，赋予不同的权重进而得到预测模型。组合模型预测的核心就是如何确定模型的权重，由于预测模型中预测值与实测值之间的残差具有不确定因素，而熵值法在组合模型中有较好的适用性[22]。其计算公式为：

(9)

(10)

(11)

di=1-hi,

(12)

(13)

3 结果与讨论

3.1 数据预处理结果

原始光谱数据受到噪声、样本背景和其他无关成分等干扰，选用合适的预处理方法能够消除噪声，提升模型预测能力。因此在建立重金属定量反演模型中，光谱数据预处理十分重要。对原始光谱进行S-G平滑处理，光谱波段范围为350～2 500 nm，由于光谱在采样过程中光谱波段两端产生较大的噪声，为此，剔除了350～449 nm和2 451～2 500 nm范围内的波段数据，共采集2 000组波段数据，如图1所示。图2为不同预处理结果，依次为FDR、DS、MSC和CR。

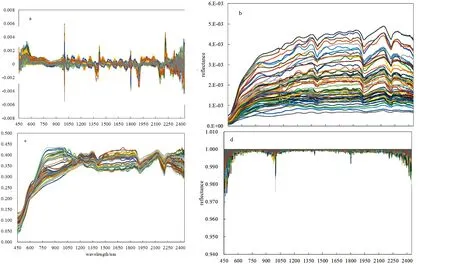
图2 不同预处理光谱反射曲线

3.2 土壤重金属含量分析

为了获悉pH和不同重金属含量之间的差异，利用SPSS软件做描述性统计，如表1所示。

由表1可知，研究区的pH范围在2.90～8.28之间，均值为6.38，土壤呈酸性居多，较少部分为弱碱性，主要是由于该研究区长期进行采矿活动所导致。从含量统计分析表中可以看出，5种重金属之间的含量差异比较明显，其中Cd和Hg的含量偏低，Cr和Ni的含量较高；从标准差来看，Cr的离散程度最大，Hg的离散程度最小；从变异系数来看，5种重金属变异系数均在30%以上，其中Cd的变异系数最大，达到114.44%，这可能是由于先前的采矿活动对周边环境影响较大，导致不确定因素增加，引起Cd分布发生异变；土壤中过量的Cd会抑制植物的生长，亦能通过食物链严重危害人体的健康，因此Cd异变应引起注意。

3.3 相关性分析

重金属在不同的波段对光谱的吸收强度也不同，因此不同波段所显示的相关性也不同。将经预处理后的光谱数据与土壤重金属含量做相关性分析，找寻显著相关的波段，以期为后期建模打下基础。相关性大小用皮尔森系数R表示，图3分别为一阶微分(a)、离差标准化(b)、多元散射校正(c)和连续统去除法(d)的相关系数曲线图。

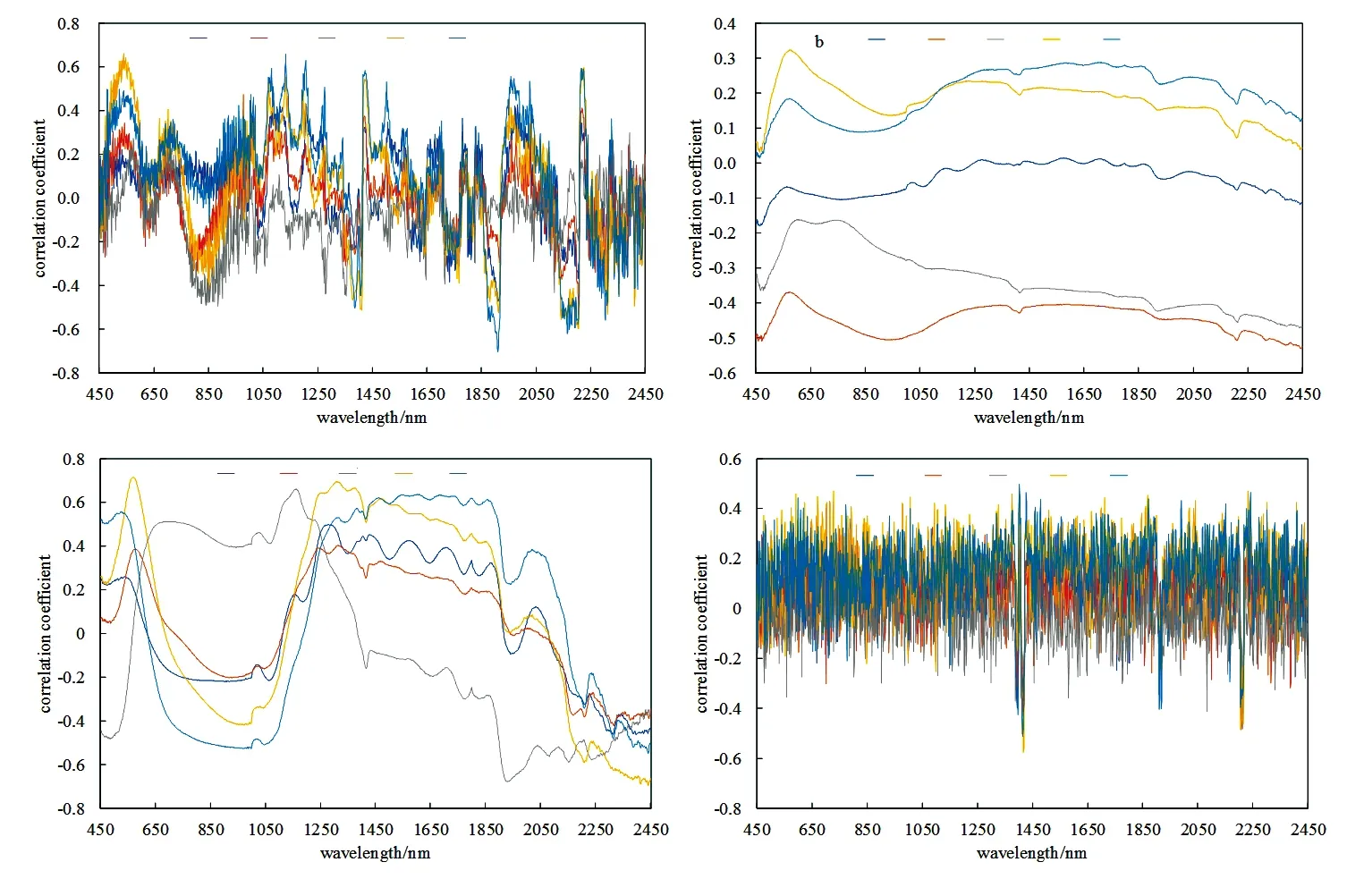
图3 土壤重金属含量与不同变换形式下光谱反射率的相关系数

从图3中可以看出，经不同的预处理，不同重金属相关性幅度变化较大，但都有不同程度的提升。经一阶微分变换，Cd、Cr、Ni、As、Hg相关性较原始光谱相关性均有所提高，对Cd和Cr相关性提高最为明显，在1 910，2 206 nm处绝对值分别达到0.475和0.532，Hg相关性在1 910 nm处达到极大值，为-0.706；5种重金属与光谱曲线的相关性系数基本都低于0.6，但大部分波段达到了水平为0.05以上的显著相关，部分波段达到水平为0.01以上的极显著相关。经离差标准化变换，5种重金属相关系数没有一阶微分提升明显，但多种重金属相关性整体提高，以Cr和Ni最为明显，Cr波段相关性绝对值整体位于0.4以上，Ni为0.3以上；对于Cd、As和Hg而言效果不为明显，其中Cd效果最不理想。经连续统去除法变换后，Cd、Cr、Ni、As和Hg在1 394，2 208，2 212，1 418，1 415 nm处达到极值，分别为-0.398，-0.484，-0.481，-0.57，-0.513，相关性虽说有所提升，但并不是最佳。经多元散射校正变换后，Ni和As相关性极好，相关系数分别在1 929 nm和568 nm处达到极值，为-0.679和0.715，整体波段也表现较高的相关性；Hg相关性在1 600 nm处达到极大值0.636，未有一阶微分达到的极大值高，但整体波段达到了很好的相关性，有一半波段相关性绝对值位于0.5以上；Cd在1 279 nm处达到极大值0.498，较比其他3种预处理，多元散射校正效果达到最佳；Cr在2 316 nm处达到极值-0.423，提升效果不为明显。总体来说，经多元散射校正变换后，多种重金属达到极高的相关性，表明多元散射校正能够有效去除噪声以及由散射带来的基线漂移等干扰，增强与样品成品相关的光谱信息[23]。

3.4 单一模型建立与分析

利用K-S算法将样本划分为建模集和验证集(建模样本50个，验证样本15个)，对样本进行交叉验证。通过对光谱数据不同的预处理做相关性分析，选择相关性较大和显著性波段分别用于PLS、ANN和RF模型的建模。采用决定系数(Determination coefficient,R2)、均方根误差(Root mean square error,RMSE)和相对分析误差(Relative percent deviation,RPD)指标对模型进行精度评定。其中决定系数作为数据拟合程度的一个评定，越接近于1，效果越好；均方根误差反映预测数据的精密度，用来衡量预测值与真值之间的偏差，RMSE越小表明预测精度越高；相对分析误差指预测偏差，它是标准差与均方根误差的比值，RPD的高低反映模型的预测能力，当RPD>2.0时，模型的预测能力很好，当2.0>RPD>1.5时，模型的预测能力一般，当RPD<1.5时，表明建模失败[24]。表2～表4依次为PLR、ANN和RF建模结果。

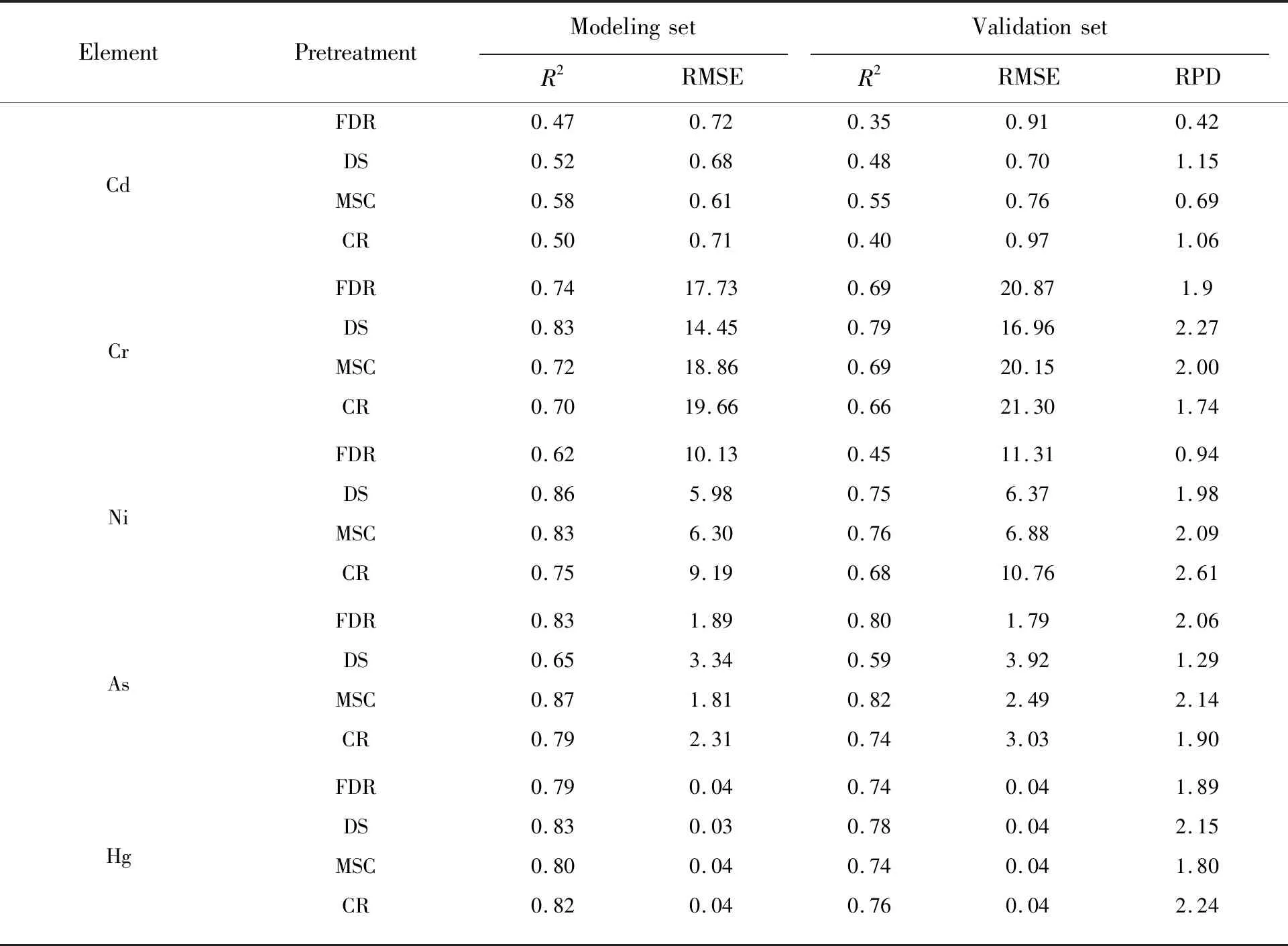
表2 偏最小二乘模型(PLS)

表3 人工神经网络模型(ANN)

表4 随机森林模型(RF)

从表2～表4中可以看出，不同的预处理对3种建模方法来说差异较大，从验证集的R2、RMSE和RPD来看，多元散射校正结合随机森林建模，R2与RPD普遍达到了0.80和2.0以上。偏最小二乘模型预测效果一般，其中As经多元散射校正变换后效果最好，R2与RPD分别为0.82和2.14。离差标准化结合神经网络对于含量相对较高的Cr、Ni预测效果较好，R2和RPD最高达到0.83和2.8，表明在进行重金属高光谱含量估算中需要考虑重金属含量对建模反演效果的影响。较比前两种建模方式，随机森林表现了优异的估测能力，经多元散射校正变换多种重金属的R2和RPD有明显提升，其中As效果最好，R2、RMSE和RPD分别达到0.89，2.00，2.77，其次是Hg、Ni和Cd，R2均达到0.80以上，Cr较比其他3种预处理变换效果无明显差异。

根据以上分析可知，结合MSC和RF的优势，相比其他预处理，MSC-RF模型整体来说要略胜一筹，其次DS-ANN对重金属含量相对偏高的元素也表现出了较好的预测能力。总体来说，采用多元散射校正结合随机森林建立的重金属反演模型效果最好。

3.5 组合模型与验证结果

单一模型自身存在一定的局限性，而组合模型能够“取长补短”，发挥多种模型的优势[25]；组合模型的关键问题在于单一预测模型的选取以及相应权重系数的确定，本文针对不同重金属，分别选取两种较优单一模型，利用熵值法确定模型权重系数，结果如表5和图4所示。

表5 组合模型参数

Notes：Yrepresentative predictive value，Capital letters represent models，The subscript represents the preprocessing transformation.

图4 土壤重金属含量较优模型与组合模型预测散点图比较

熵值法能够根据单种预测模型预测误差序列的变异程度来确定组合模型的权重系数而且计算简单[26]，提供了一种客观赋权的方法。通过利用熵值法进行模型组合，从表5中土壤重金属含量的预测结果可以看出，验证集精度相比传统单一模型验证集精度有了显著的提高，其中As的R2值达到最高，相比其最优模型R2由0.89提高至0.91，RMSE由2.00降低至1.85；对于Cd、Cr和As线性模型和非线性的组合表现出了优异的估测能力，尤其对于Cd，R2和RPD分别由最优单一预测模型的0.83和1.76提升至0.85和2.39，RMSE由0.18减少至0.16；表明利用熵值法确定的组合模型估算土壤重金属含量是可行的。图4为重金属含量实测值与预测值散点图，散点越接近于1∶1对角线，效果越好，从图中可以看出，组合模型散点较多集中在对角线附近，且散点趋势线与对角线之间的角度差很小，表明结合多种模型能够对重金属含量的预测产生一个很好的效果。由于土壤为矿物质、有机质和水分等物质组成的复杂有机整体，各成分之间相互影响、相互作用，土壤光谱易受区域性和地域性影响，因此不同区域内的土壤光谱有所差异。本文以四川古蔺矿业废弃地复垦土壤重金属为研究对象，所建立的重金属含量反演模型在其他区域的适用性还有待于进一步研究。

4 结 论

针对高光谱反射率反演土壤重金属含量问题，本文采取4种预处理变换并结合PLS、ANN和RF 3种建模方法建立矿业废弃地复垦土壤反射率与土壤重金属的单一定量模型，并采用熵值法进行较优模型组合，得到如下主要结论：

(1)原始土壤光谱反射率和重金属之间的相关性较弱，经不同预处理变换后，部分波段相关性有了明显的提升；其中MSC总体效果较好，对As和Ni最为明显，相关性系数极值达到0.715和-0.679，且整体波段都取得了较好的相关性；其次FDR对Hg较为明显，相关性极值达到0.706；DS对重金属含量相对偏高的Cr的相关性起到了很好的提升效果，绝大部分波段相关性系数位于0.4以上，最大极值达到-0.530。

(2)预处理变换和模型的选取不同对预测结果影响较大，利用3种精度指标对模型进行评价，其中MSC-RF反演效果最好，验证集As、Hg、Ni和Cd的R2、RMSE和RPD分别达到：0.89，2.00，2.77；0.84，0.03，2.52；0.83，4.78，2.72；0.83，0.18，1.76；DS-ANN对Cr效果较好，3种精度指标分别为：0.83，15.66，2.19；利用MSC和DS结合非线性模型效果要优于线性模型，由于这两种变换能够显著提升整体波段的相关性，为RF和ANN模型提供了大量的输入参数；结果表明，针对不同的建模应选取适宜的预处理变换方法。

(3)从单一模型和组合模型预测结果来看，单一模型虽具有运算速度快、操作简便等优势，但组合模型能综合利用多种模型信息，减弱单一模型中随机因素带来的影响，应提高组合模型在土壤光谱预测方面的应用性。熵值法根据预测模型的变异程度确定权重，避免了权重确定的主观性，客观地反映了单一预测模型在组合模型中的重要性，利用熵值法进行两种较优模型组合，较传统单一模型，精度指标均有所提高，表明采用熵值组合模型对土壤重金属含量进行预测效果更好。