非局部时滞反应扩散方程行波解的存在性分析
张敏华
(阳光学院基础教研部 福建福州 350015)
在客观世界里普遍且大量存在时滞反应现象与非局部空间作用,这可以构建非局部时滞反应扩散方程来进行描述。非局部时滞反应扩散方程结合了时间与空间上的非局部现象,被广泛应用于生态学、传染病学等多个领域,也成为了高等数学应用研究的重点与难点内容,相较于非局部反应扩散方程更为复杂[1]。形如u(x,t)=u(x+ct)的行波解是非局部时滞反应扩散方程一类重要的稳态解,行波解能揭示非局部时滞反应扩散方程重要性质,且由于其具有空间平移不变性的特征能有效表现与描述自然界内的振动与有限速度传播现象,如可以表现生物物种的入侵过程以及传染疾病源的传播规律等,可见非局部时滞反应扩散方程的行波解具有很强的应用实践价值。目前伴随着非局部时滞反应方程应用强度进一步深入,为了解非局部时滞反应方程的重要性质以及解决实际应用问题,非局部时滞反应方程的行波解展开研究是非常必要的。对此,在反应扩散方程理论的基础上,着重分析了具有时滞的反应扩散的SIR 模型以及非拟单调时滞非局部扩散系统的行波解存在性。
一、文献综述
自然界中扩散中普遍存在时间滞后和空间非局部作用,为进一步解决与描述这一现象,在上个世纪70年代起研究者将时滞与局部扩散相结合,如Levin将扩散反应引入到单种群模型中得到了具有时滞扩散Logistic 模型[2]。但是随着研究的深入发现提出的局部有限时滞模型具有明显的局限性,模型中时滞与空间扩散是彼此独立的。但是在实际现象中,在过去的时间里个体的空间内位置并不是一成不变的,而是随着时间变化个体在空间内是不断发生变化。针对这一问题Britton(1989)进行了全方位的考虑,利用空间加权平均的思想提出如下单物种种群模型,其中g是指定函数,卷积项(g*u)等于
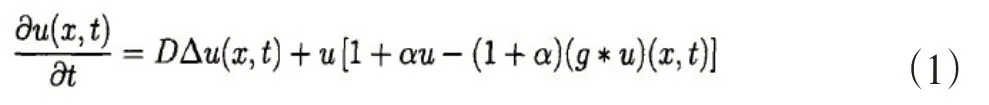
后来研究学者将这类具有结合了时空加权平均时滞项的反应扩散方程统称为非局部时滞反应扩散方程。随后Smith和Thime(1991)通过采用对具有年龄结构的种群模型沿着种群特征积分的方法推导了一个具有成熟结构的种群模型。随后这种方法被So(2001)、Weng(2003)等人有效推广至连续空间以及具有无限多个离散的斑块环境下非局部时滞反应扩散方程。此后,非局部时滞反应扩散方程被应用于多个领域,研究也愈发深入,包括Al-Omari与Gourley.S(2003)构建的Loth-Volterra型两物种竞争模型,Lian(2003)建立的具有全局交互效应时滞反应对流扩散模型[3-4]。
在非局部时滞反应扩散方程行波解研究上,Xiao与Ruan(2004)通过线性链技术与几何扰动理论对满足的一类传染病模型在且b大于a的条件下模型行波解存在性进行研究,研究结果显示波速不小于时存在连接模型两个平衡点的行波解5];J.Zhang(2007)同样采用以上技术与理论方法对方程行波解的存在性进行了研究[6]。Xu和Zhao(2005)采用相平面以及谱理论等技术方法对一类传染病模型的双稳波前解的存在性与全局渐近稳定性等进行了研究。
对非局部时滞反应扩散方程行波解的研究具有很强的实际应用价值,近年来已成为研究的热点问题。国内众多学者对这类方程的行波解也持以了很高的关注度,对行波解的存在性、稳定性以及渐进性等展开了丰富的研究。马万彪等人(2013)通过采用惯性流行理论对具有小离散时滞反应扩散方程的行波解的存在性进行了证明,结果显示该方法能有效避免反应项的假设设定问题[7];张卫国等人(2016)对一类具有时滞Lotka-Volterra系统的行波解存在性通过简化的方式寻找竞争系统模型的上下解[8];邹霞(2018)则针对一类具有时空时滞的传染病SIR模型,通过Schauder不动点定理以及求极限等方法来判断行波解的存在性[9];李成林(2017)对具有Neumann边界条件扩散反应的三种物种时滞系统采用特征值法对系统的稳定性进行了分析,并通过寻找上下解的方式证明在波速c足够大时存在连接零、正两个平衡点的行波解[10]。
对非局部时滞反应扩散方程行波解研究是当前的重点与难点,取得了一定的研究进展。但是纵观目前的研究结果来看,国内对于非局部时滞反应扩散方程行波解的研究还处于起步阶段,对此针对这一现状有必要对非局部时滞反应扩散方程行波解的存在性展开更深入的探讨来丰富行波解的理论研究与增强应用能力,具有重要的理论与实践研究价值。
二、非局部扩散时滞反应SIR模型行波解的存在性
传染病直接影响了人类的身体健康,传染病在传播过程中不仅存在时间滞后,也与携带者、易感染着等人口的空间位置是紧密相关的,具有典型的时间——空间关系,对此探讨一类具有非局部扩散时滞反应的SIR模型,模型如下所示:
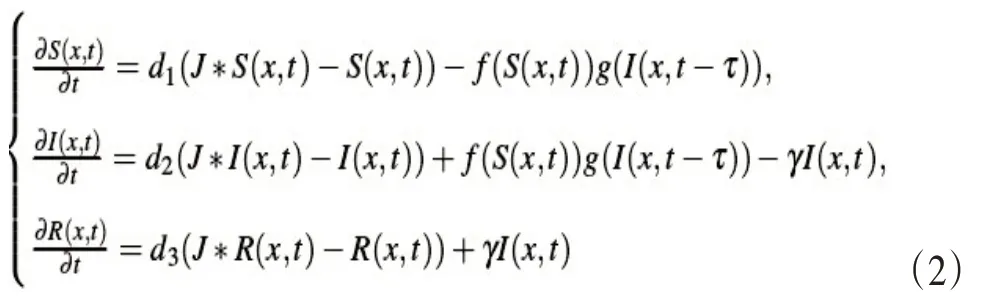
该SIR模型还满足以下条件:
(H1)当S≥0时,f’(S)为有界正函数;

对上述模型(2)行波解的存在性进行证明,即需寻找行波方程(3)的存在性,也就是寻找方程(3)满足边界条件的解,其中为大于0的常数,代表了感染前易感人群的密度。
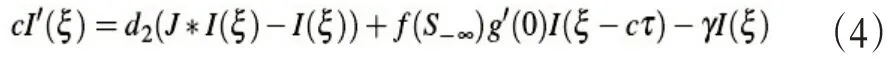
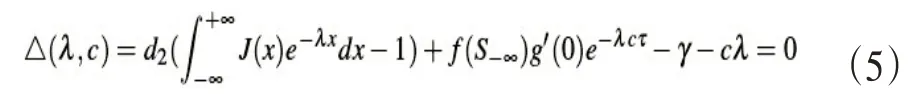
因此通过简单的计算可得出以下引理。
引理1设定大于0,则有大于0的C*与λ*使得
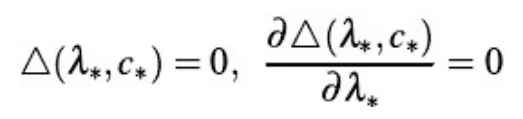
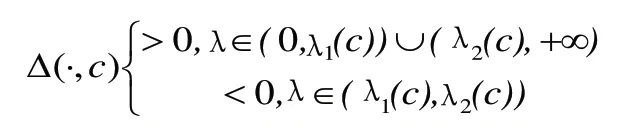
引理2存在任意大于0的常数C,对任意大于的X 都有和
根据Schauder不动点定理可知(SX,IX)为算子的不动点,对于任意属于(-X,X)范围内下的ξ,不动点(SX,IX)满足下列关系式:
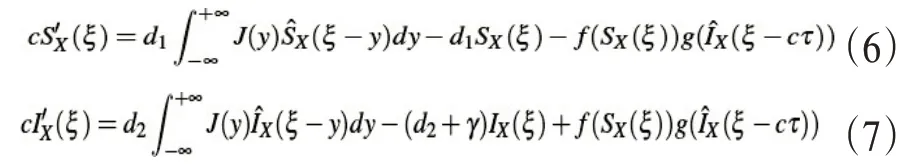
对式(6)进行(-X,X)区域内的积分可得
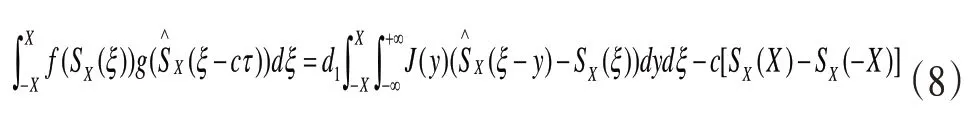
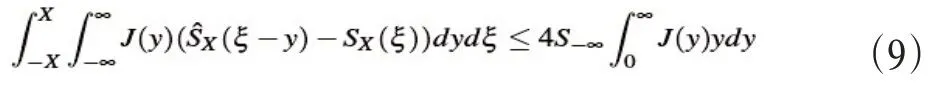
对此可以得到下式(10):
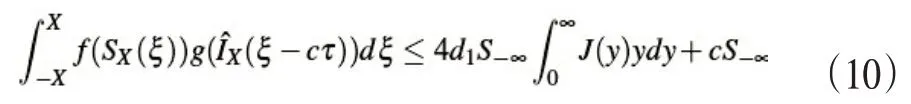
同样对式(7)进行(-X,X)积分,得到如(11)式
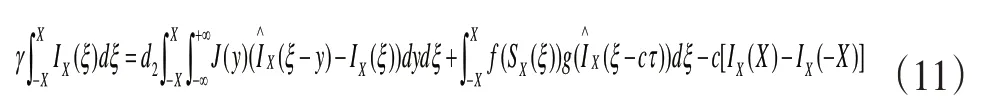
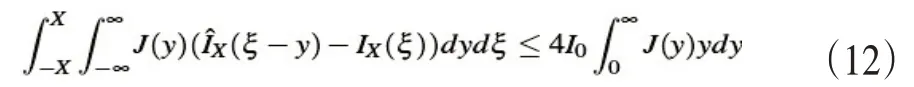
联合式(10)至(12)式可得
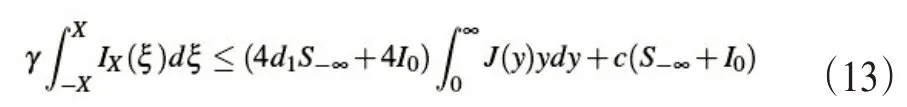
根据前面的条件(H3)可以了解到式(13)是右侧是有界的,故而存在一个大于0的常数C使得
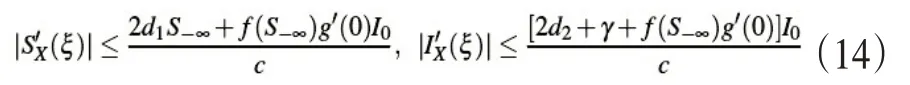
因此存在两个正常数L1与L2,对于属于[-X,X]范围内的ξ和η有
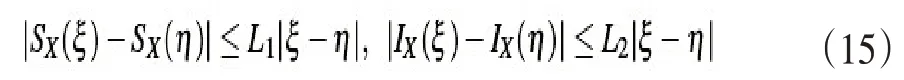
根据式(6)可得到
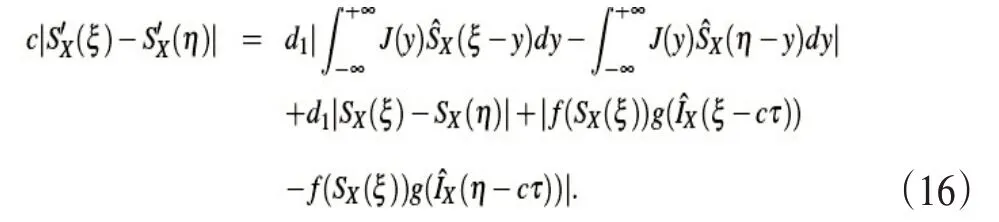
又因核函数J 是Lipschitz 连续,因此存在大于0 的Lipschitz 常数 LJ,使得,其中 suppyJ=[-N,N],N 为大于0的常数,故经过计算与变换有

并根据式(16)可以得到如下式(19)
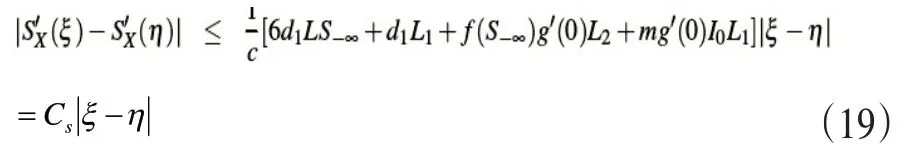
同理对式(7)作同样处理最终可得到式(20)和(21),如下所示:

联立式(7)、(14)和(21)可以得到
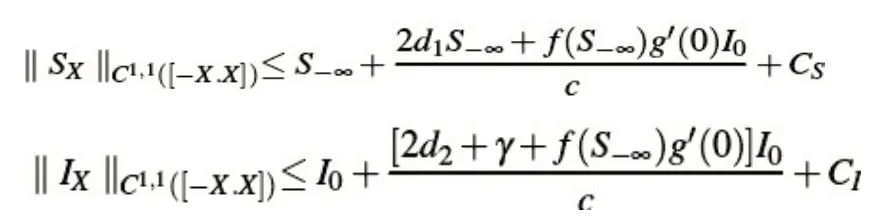
(二)行波解的存在性分析。本次证明中假设C>C*,且R0>1对此进行SIR模型的行波解的存在性分析,提出以下定理。
定理设定大于1,那么对于任意大于C*的C,SIR模型存在行波解满 足并且有
证明过程如下所示:

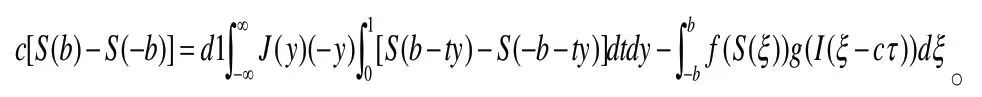
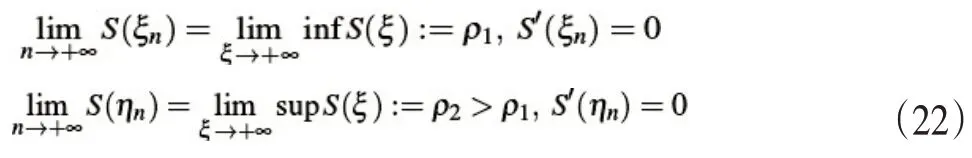
将和带入到式(3)第一个方程可得
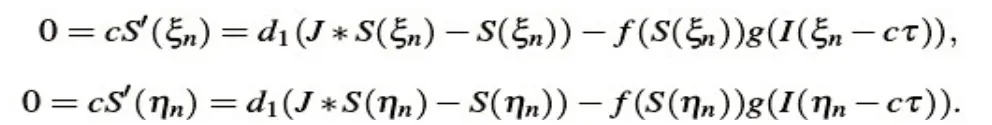
在凭借文献[12]的计算方法可知,当y属于suppyJ时,则有下式(23)
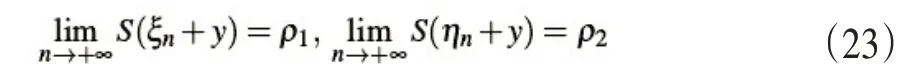
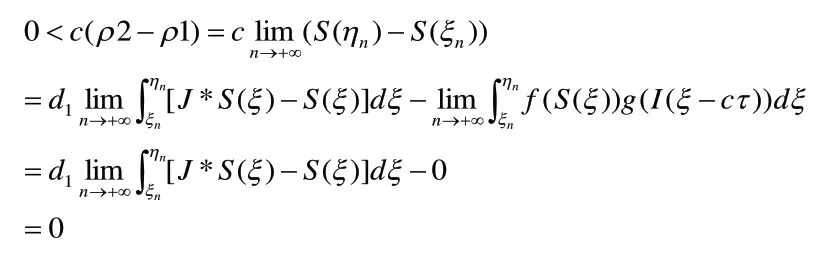
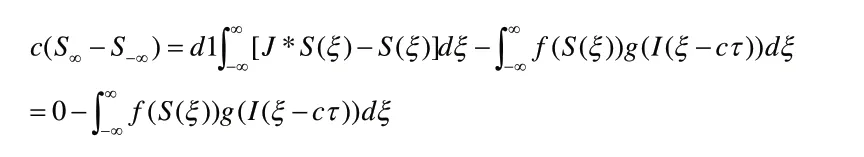
进一步简化可得到式(24)
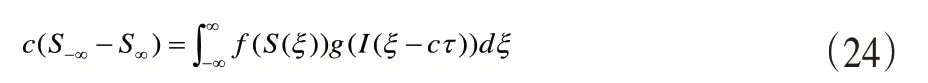
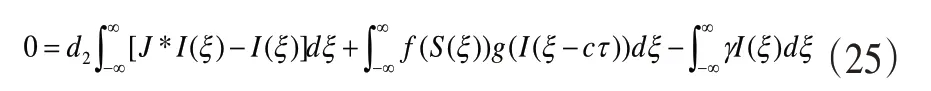
三、结论
当前对非局部时滞反应扩散方程的行波解性质研究成为了高等应用数学的热门研究话题。本文基于一类具有非局部扩散的时滞传染病SIR模型,通过Schauder不动点定理、Fubini's定理以及极值法等方法对该模型行波解的存在性进行了分析与证明。通过研究发现本次研究模型存在满足边界条件的形态如的稳态解,证明结果显示能方法能有效解决该类SIR模型行波解的存在性问题。

