基于Petri网的车库管理系统的建模优化
梁 亚 王丽丽
(安徽理工大学数学与大数据学院 安徽淮南 232001)
随着基于Petri网的工作流的业务流程模型的应用场景越来越丰富,大量研究开始着眼于使用Petri网进行建模优化。文献[1]介绍了工作流管理作为Petri网的应用领域,介绍了有关工作流验证的最新结果,将其用于实际场景。文献[2]介绍了一种在Petri网中进行可达性检查的技术,利用组合性来提高一些众所周知的例子的性能。文献[3]从行为轮廓的角度出发,对Petri网的多方面性能进行了分析,为优化业务流程模型的性能提供了有效的方法。文献[4]提出了Petri网行为轮廓的概念,将其用于实际可以弥合业务需求于系统实现之间的差异。在工作流网的基础上可以对先前的流程模型进行优化[5],比如通过对工作流网添加抑制弧从而对WFPN进行优化。
本文结构如下:第二部分内容介绍了Petri网及行为轮廓的相关概念,第三部分通过增加变迁结构对原始简单模型进行优化,达到能够处理复杂情况的目的,第四部分使用PIPE软件检验优化后的模型,验证正确性与合理性,第五部分对所做研究进行总结,并对未来工作的一个展望。
一、基本概念
定义1[6](流程模型)设∑(A,ai,a0,C,F,T)为一个六元组的流程模型:
A为一个非空的活动变迁节点集,C为控制流节点集,A和C不相交;
ai∈A为一个最初的活动变迁,a0∈A为一个最终的活动变迁;
F⊆((A{a0})∪C×(A{a})∪C为流关系;
T:C→{and,or,xor}流程模型控制流的类型。
定义2[7](变迁发生规则)一个网系统是一个标识网∑=(S,T;F,M),并具有下面的变迁发生规则:
(1)对于变迁t∈T,如果
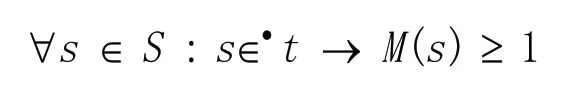
就说变迁t在标识M有发生权,记为。

定义3[6](行为轮廓)设有网PN=(P,T,F,C),初始标识为M0,对于任意给定的变迁(t1,t2)∈(T×T)满足下列关系:
1)若t1≻t2且t2⊁t1,则称t1、t2为严格序关系,记作t1→t2;
2)若t1⊁t2且t2≻t1,则称t1、t2为严格逆序关系,记作t1→-1t2;
3)若t1⊁t2且t2⊁t1,则称t1、t2为排他序关系,记作t1+t2;
4)若t1≻t2且t2≻t1,则称t1、t2为交叉序关系,记作t1‖t2;
定义4[8](可达性)已知Petri网,如果存在,使,则称为从M直接可达的。如果存在变迁序列和标识序列使得
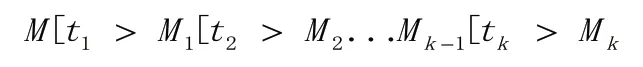
二、通过增加控制结构对模型进行优化分析
对于普通车库(如图1,各个变迁意义见表1),当车辆达到时,闸机处摄像头会拍摄车牌号并识别,系统查询后台,返回车库内剩余空车位。如果没有剩余车位,则拒绝车辆驶入;如果有剩余,则允许入库,闸机开启,并开始计时。当车辆驶出时,闸机处摄像头再次识别,计算停放时间及费用后,提示缴费。在司机缴纳完费用后,闸机开启放行,允许出库。
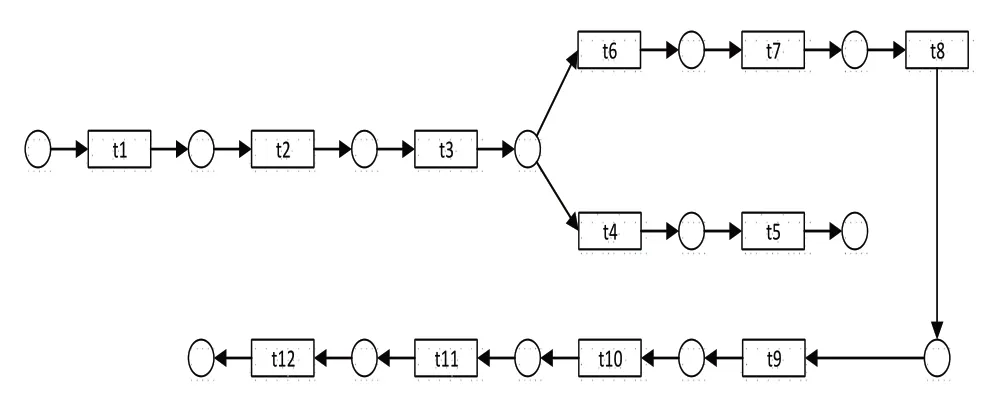
图1 普通车库管理系统模型

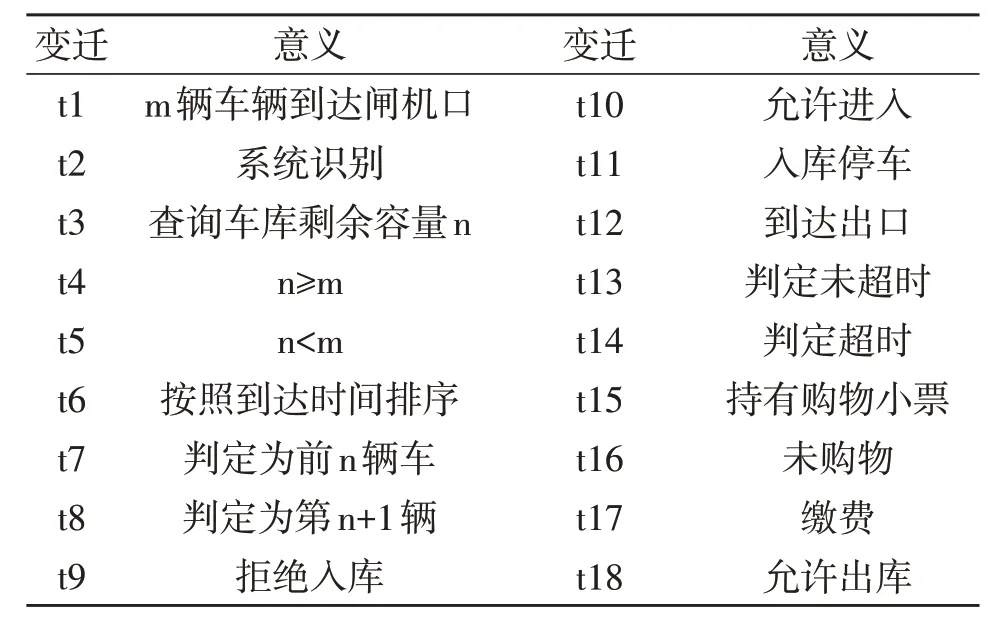
表1 普通车库管理系统模型中各变迁符号及意义
但是这种系统只对在单入口的简单车库起作用。某超市车库具有n个闸机,高峰时期,可能每个入口都至少排有一辆车,如果此时车库内剩余大量车位,闸机口可以尽数放行;但是如果剩余车位不足m个时,就需要对车辆到达时间进行分析,这时原始简单系统就无法满足实际需求,并且,凡在超市购物者,凭小票可以免费停车2个小时。这样一来,就给系统带来了新的挑战。
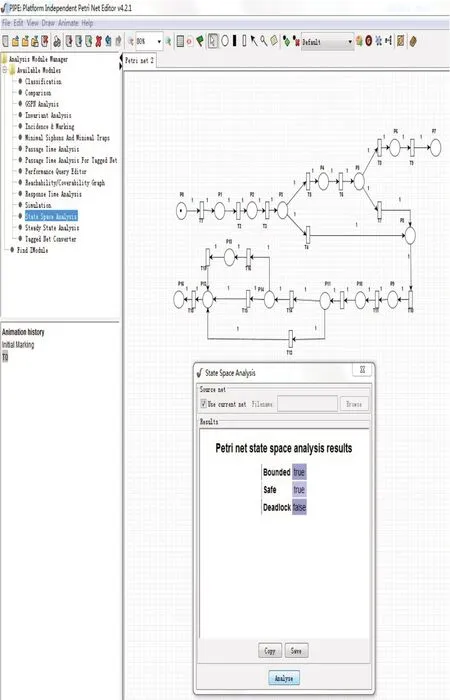
改进后的系统很好的解决了这些问题(如图2,各个变迁意义见表2)。当闸机处摄像头识别到车辆到达时,向系统回传车牌号及车辆到达时间。系统查询数据库,返回车库内剩余空车位m。当n≥m时,全部允许进入,当n 图2 优化后的多入口车库管理系统模型 表2 优化后的多入口车库管理系统中各变迁符号及意义 PIPE是一个支持广义随机Petri网模型设计和分析的开源工具,本文使用PIPE模拟运行模型,并从状态空间分析角度对模型进行分析,结果如图3所示,优化后的模型具有有界性和安全性,并且无死锁。 图3 PIPE运行及分析 本文在只能管理具有一个入口的车库原始简单模型的基础上,保证原有弱序关系,结合行为轮廓的理论,增加控制结构,对入库过程和出库过程进行优化,能够更好的管理车库的车辆。但是文章仅从控制流的角度进行分析,面对系统中可能出现的变化,还需要结合配置进行改进。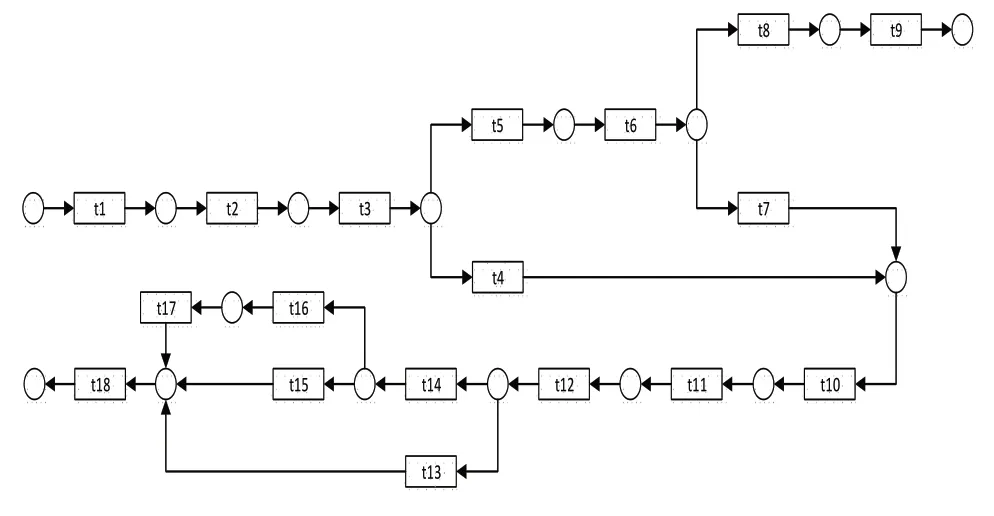
三、使用PIPE对模型进行仿真及状态空间分析
四、结语

