过冷水流经通道的闪蒸临界流模型研究

吕玉凤，赵民富，杜开文

(中国原子能科学研究院 反应堆工程技术研究部，北京 102413)

冷却剂丧失事故(LOCA)作为反应堆的设计基准事故之一，是反应堆安全分析的重要方面。反应堆运行在高温、高压条件下，发生LOCA时，冷却水从破口喷出，回路迅速降压，回路的高温水急剧汽化，形成气液两相流，破口处将会发生临界流动[1]。破口处的质量流量决定着反应堆冷却水系统的装量和能量丧失速率，进而强烈影响着系统压力、堆芯冷却剂温度和燃料包壳温度的变化规律，从而对事故后果起重要作用。在先进压水堆中，自动卸压系统(ADS)是一项重要的非能动安全技术[2]。ADS的流体排放也涉及临界流动现象，此时的流动特性控制着事故的进程和安全系统的动作，与事故的缓解密切相关[3]。因此，清楚认识临界流动现象并建立合适的临界流量计算方法，是核反应堆安全分析程序发展中的重要课题。

迄今为止，有关两相临界流动的研究已进行了大量工作，并提出了很多分析模型和计算关系式，Abdollahian等[4]、Saha[5]对这方面工作做了非常详尽的评述。文献[6]中对现有临界流模型进行评价，结果表明热力学平衡模型(包括均匀平衡模型、滑移平衡模型)在预测滞止状态为饱和或过冷液体流过短管及喷嘴时，产生极大的误差，有些工况误差高达100%。对于短管及喷嘴的临界流动，两相膨胀非常快，以致相间不能达到平衡状态，汽化核心在过热液体及通道的壁面上形成并长大。因此，需发展既反映相间速度差异(即力学非均匀)，又反映温度差异(即热力学非平衡)的数值模型来预测临界流量。

热力学非平衡模型可分为非平衡经验模型(如Henry-Fauske模型[7])和反映热力学非平衡物理机制的两流体模型。Henry-Fauske模型引入经验系数N来修正热力学平衡含汽率xe而得到其真实含汽率，这相比热力学平衡模型有了较大改善。但该系数仅是对实验数据的关联而未反映非平衡机理。Abdollahian等[4]采用Marviken数据对Henry-Fauske模型进行评价时，为使模型计算结果匹配实验数据，对N进行了修改，N的取值范围为7.1xe～100xe。两流体模型试图从临界流动的机理出发，分别对气液两相的连续、动量、能量方程进行描述，并补充一些基本结构关系式从而构成封闭方程组，如两相间的相互作用力、相间传热特性、相界面动量传递等。两流体模型可反映相间的热力学非平衡性，非平衡的一个关键问题是汽化(闪蒸)现象，包括闪蒸起始点、汽泡初始直径、汽核密度及汽泡的增长规律。由于两相流微观机理的复杂性，目前对这些物理量的研究尚不充分。在Richter[8]、Dobran[9]、Schwellnus等[10]提出的考虑热力学非平衡效应的两流体模型中，均部分地假设了未知参数数值来“符合”实验数据。

本文从气液两相的连续方程、动量方程及能量方程出发，建立两流体六方程热力学非平衡模型，对现有计算闪蒸起始点位置和过热度的公式进行比较分析，最终选取较合理的计算公式。在泡状流区域，将汽泡增长方程与基本方程联立求解，可较准确地反映汽泡增长规律。

1 两流体模型

本模型由6个方程构成：气相和液相的质量守恒方程、气相和液相的动量守恒方程、两相混合物的总能量守恒方程、气相的能量守恒方程。另外在泡状流区补充1个汽泡增长方程。主要假设有：1) 一维绝热流动；2) 在两相流动中液相是饱和或过热的，气相是饱和的，温度等于当地压力下的饱和温度；3) 忽略两相间的黏性应力及黏性耗散。

1.1 基本控制方程

Dobran[9]给出了一维、稳态的两相流动守恒方程。

液相质量守恒方程：

(1)

气相质量守恒方程：

(2)

液相动量守恒方程：

Fwl+Flg-Fli-(1-α)ρlgsinθ

(3)

气相动量守恒方程：

-Fwg-Flg-Fgi-αρggsinθ

(4)

总能量守恒方程：

(5)

气相能量守恒方程：

(6)

式中：A为通道截面积；α为空泡份额；cpl为液相比定压热容；Fwl、Fwg分别为通道壁面与液相、气相摩擦引起的压力损失；Flg为相界面相互作用力；Fli、Fgi为相界面上液相、气相由于质量交换引起的动量传递；g为重力加速度；G为质量流速；hl、hg分别为液相和气相的比焓；p为压力；Tl为液相温度；ul、ug分别为液相和气相的速度；qi为单位体积内界面传递的热量；θ为通道轴向与水平方向夹角；ρl、ρg分别为液相、气相的密度；x为含汽率；z为通道轴向距离。

上述方程涉及到6个变量：α、x、ug、ul、p、Tl。在泡状流区域(0<α≤0.3)，引入第7个变量，汽泡直径db。假设平均汽核密度为N，则有：

(7)

将式(7)与式(1)联立，可得：

(8)

当处于泡状区时，将式(1)～(6)与式(8)联立，构成七方程组，db作为第7个变量增加到方程组中，db随x和α的变化而变化；当不在泡状区时，方程组直接由式(1)～(6)求解，变为6个守恒方程。

在Richter[8]、Dobran[9]提出的两流体模型中，假设汽核密度N为一常数。而在本模型中将式(1)～(6)与式(8)联立求解，N与db、x及α相互关联，是不断变化的，因而能更好、更真实地描述泡化过程。

为求解上述变量，需给出Fwl、Fwg、Flg、Fli、Fgi、qi结构关系式。状态参数ρg、ρl、hg、hl、cpl、∂ρg/∂p、∂ρl/∂p、∂hg/∂p可由水物性计算软件得到。

1.2 结构关系式

1)Fwl、Fwg

Fwl通过两相摩擦压降倍率与液相单独流过通道时的压降梯度联系，即：

(9)

(10)

式中，fl0为单相摩擦系数，由下式确定：

(11)

式中：Re为雷诺数；ε/D为壁面粗糙度，由于气相和壁面不是直接接触，故可忽略气相和壁面的摩擦力，即Fwg=0。

2)Flg

Flg主要由两方面组成：相界面上的拖拽力FD和两相间相对加速引起的虚拟质量力FVM[12]。

Flg=FVM+FD

(12)

FVM=CVMρlαVM

(13)

(14)

(15)

λ=2(1-α)

(16)

式中：CVM为虚拟质量力系数；λ为系数。

在泡状流区域，FD为：

(17)

(CD)1-α=CD(1-α)-4.7

(18)

CD=0.44Reb>1 000

(19)

式中，CD为汽泡与汽泡之间的相互作用力系数。

对于环状流区域，FD为：

(20)

式中，界面拖拽力系数Cfi为：

Cfi=0.005[1+75(1-α)]

(21)

CD和Cfi之间的关系为：

(22)

对于弹状流区，两个转换点的数值变化很大，采用指数插值形式。

3)Fli、Fgi

Fli、Fgi如下：

(23)

(24)

式中，系数η取0.5。

4) 相界面间的传热qi

单位体积内的相界面传热表达式为：

qi=aihi(Tl-Tg)

(25)

式中：ai为单位体积的气液两相相间面积；Tl为液相温度；hi为相间传热系数。

对流传热系数在不同的流型中不同，在泡状区由下式决定：

(26)

式中：Nu为努塞尔数；kl为液相导热系数；Pr为普朗特数。

对于环状流区域，相界面传热系数表达式为：

(27)

对于弹状流的传热系数，可通过线性插值的方法得到。

1.3 边界条件

Fraser等[13]的研究表明，闪蒸点的位置和过热度对临界流量有显著的影响。对于面积不变的喷管，发生闪蒸起始点的位置并不是固定的，而是与上游滞止参数、通道结构、壁面条件、凝结气体等因素有关。

在两流体计算模型中[8,10]采用的计算闪蒸起始点过热度的公式为：

(28)

式中：Tsat为饱和温度；σ为该温度下的表面张力；vlg为气、液两相比容之差；slg为气、液两相比熵之差；文献中一般设置闪蒸起始点初始直径db为25 μm。

但按照该公式计算的闪蒸起始点过热度一般很低。文献[6]根据试验数据对现有闪蒸点过热度的公式进行评价表明，Alamgir & Lienhard公式[14](式(29))计算的过热度与短喷管的试验数据符合较好。并且，该式可体现上游滞止参数、卸压速度等对过热度的影响，更能反映真实情况。因此，本文首先采用Alamgir & Lienhard公式计算闪蒸起始点的压力：

pFi=psat(T0)-

(29)

式中：pFi为闪蒸起始点压力；T0为初始温度；Tr=T/Tc，Tc为临界温度，Tc=647.3 K；k为波尔兹曼常数，k=1.380 54×10-23；Σ′为卸压速度。

求得pFi之后，可按T0-Tsat(pFi)计算闪蒸起始点处的过热度。然后由伯努利方程及质量守恒方程，求得闪蒸起始点的位置zFi：

(30)

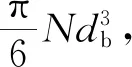
1.4 求解过程

根据上述的控制方程、状态方程和基本结构关系式，经整理可得如下矩阵方程：

(31)

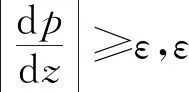
2 模型验证

2.1 与中国原子能科学研究院(CIAE)试验比较

CIAE开展了稳态临界流动试验[15]，试验段直径为2 mm，长径比(L/D)分别为1、3、6、12、20。试验压力范围为3～16 MPa，入口温度范围为30～345 ℃，入口含汽率为0～0.5。图1a为L/D=1的喷管在压力为10～16 MPa、过冷度为0～40 ℃范围内质量流速测量值与模型计算值的比较。对于大部分实验工况，程序预测结果偏低，这是因为该区域热力学非平衡效应非常严重，最大相对偏差约为10%。图1b为L/D=12喷管的模型计算值与试验结果比较，同样模型预测质量流速与试验结果符合较好。

图2示出了两相流基本参量沿管长的变化。试验工况为：初始压力为10 MPa，初始过冷度为20.1 ℃，L/D=12。可见，沿管长方向α、x、气相和液相速度是不断增加的，在接近通道出口处，α及两相速度急剧增加。

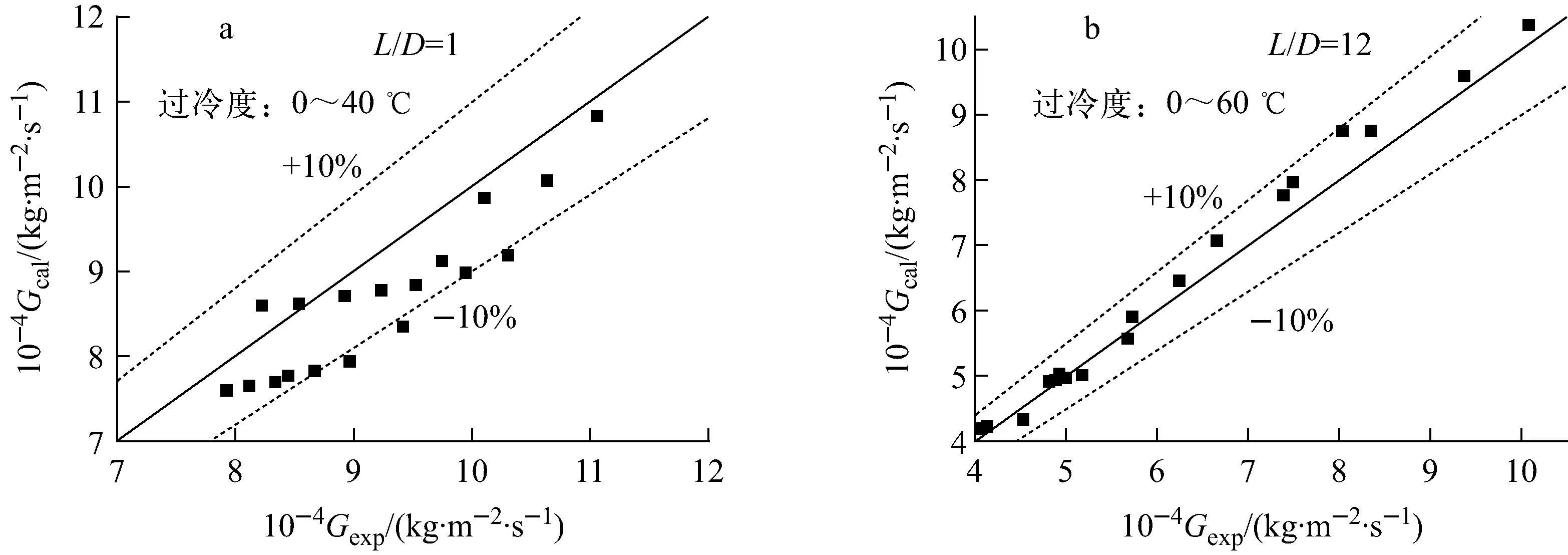
图1 模型计算结果与CIAE试验值的比较Fig.1 Comparison of model prediction and CIAE experiment results

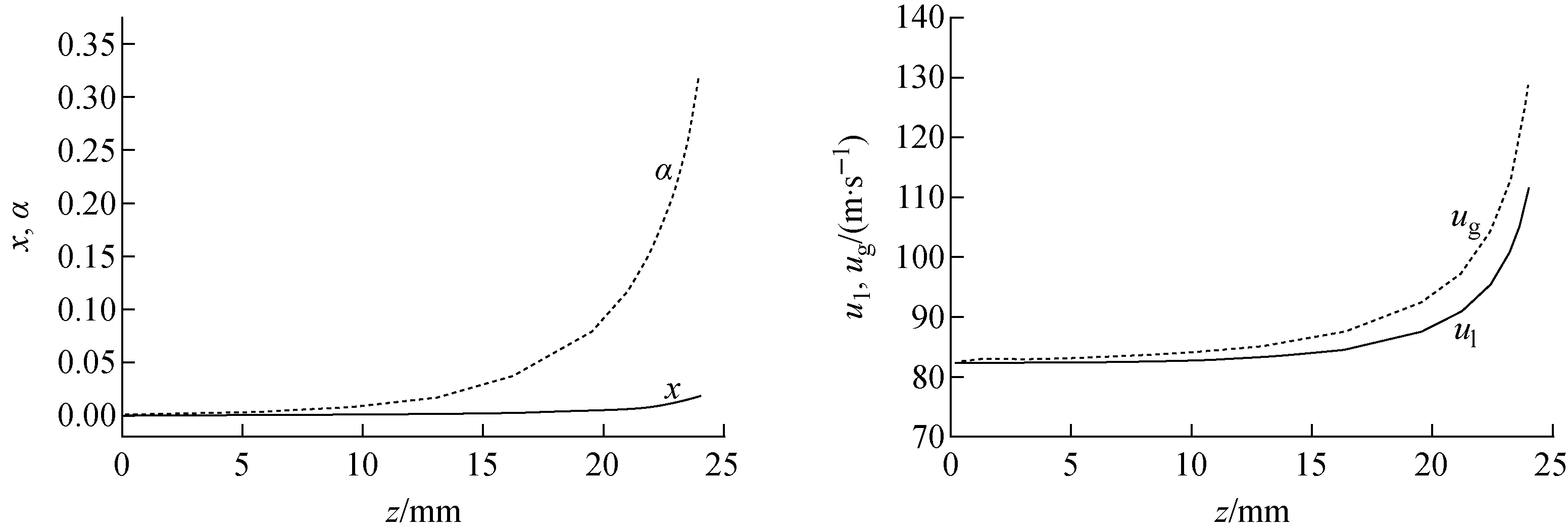
图2 两相流基本参量沿管长的变化Fig.2 Variation of two-phase flow parameter along tube

'

2.2 与Fauske实验比较

1965年，Fauske[16]采用锐角入口的喷管试验段开展了临界流动实验，试验段直径为6.35 mm，滞止压力范围为0.5～15 MPa，工质为饱和水或过冷水。图3a为Fauske采用的锐角入口试验段在不同L/D下实验结果与模型计算结果的比较。可见程序预测的质量流速与实验值符合很好，最大相对偏差不超过10%。图3b为不同滞止压力条件下Fauske实验数据与模型计算结果的比较，此处Fauske在实验中采用圆角入口的试验段，试验段直径为6.35 mm，长度为254 mm，即L/D=40，实验工质为饱和水。可见，在不同的滞止压力下模型计算结果与实验结果是比较符合的。

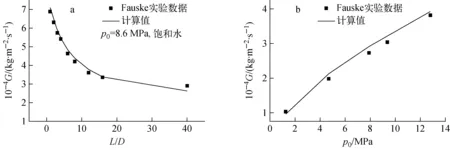
图3 模型计算值与Fauske实验值的比较Fig.3 Comparison of model prediction and Fauske experiment results

2.3 与Celata等实验的比较

图4为本模型计算的压力沿通道分布与Celata等[17]的实验数据比较。试验采用的喷管直径为0.012 5 m，L/D=97，圆角入口。图4a的实验工况为：滞止压力2.0 MPa，过冷度ΔTsub=22.7 ℃，实验测量得到的临界质量流速为23 000 kg/(m2·s)，程序计算值为23 654 kg/(m2·s)，二者相对偏差为2.8%。程序计算的压力分布与实验结果符合很好。图4b的实验工况为：滞止压力2.23 MPa，滞止状态为饱和水。实验测量得到的临界质量流速与程序计算值相对偏差为5.2%。程序计算的压力较测量值略高，可能是因为管道入口摩擦压降和两维效应对汽泡生长有较大影响，与程序中关于汽泡生长的模型描述不一致导致的。

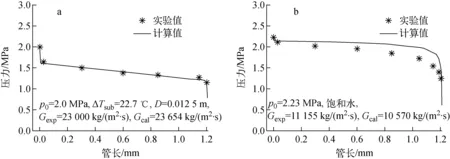
图4 模型计算压力分布与Celata等实验值的比较Fig.4 Comparison of pressure distributions between prediction and Celata et al. experiment

3 结论

本文从两相临界流动的热力学非平衡机制出发，建立了两流体临界流模型。模型做出的主要改进如下。

1) 引入了经过实验验证的计算闪蒸起始点过热度和闪蒸点位置的计算公式，可体现上游滞止参数、卸压速度等对过热度的影响，更能反映真实情况。

2) 在泡状流区域，将汽泡增长方程与控制方程联立求解，得到的汽泡直径与压力、含汽率和空泡份额有关，能比较准确地反映汽泡的增长规律，更接近实际情况。

该模型在很宽的试验范围内成功地预测了临界质量流速和压力分布，验证了模型的通用性。