基于ARIMA模型的渭南市降水量趋势分析与预测

张改红

摘要：采用ARIMA模型对渭南市1953～2013年历史降水量趋势进行模拟，优选参数，建立降水量预测模型，对2014～2018年的降水趋势进行预测。经拟合结果分析可知 ARIMA 模型能够比较好地预测渭南市年降雨量变化趋势，渭南市近些年降雨量呈现略微下降的趋势，但随着预测期的延长，预测精度降低。建议在使用ARIMA 模型预测年降雨量时，尽量保证数据序列足够的情况下，采用逐年实时校正的预测方法。

Abstract： The ARIMA model is used to simulate the trend of historical precipitation in Weinan City from 1953 to 2013. The parameters are optimized and the precipitation prediction model is established to predict the precipitation trend from 2014 to 2018. According to the analysis of the fitting results， the ARIMA model can predict the annual rainfall variation trend in Weinan City. The rainfall in Weinan City has a slight downward trend in recent years， but the prediction accuracy decreases with the extension of the prediction period. It is recommended to use the yearly real-time correction forecast method and try to ensure that the data sequence is sufficient when using ARIMA model to predict annual rainfall.

關键词：时间序列分析;ARIMA 模型;降水量;预测

Key words： time series analysis;ARIMA model;precipitation;prediction

中图分类号：P333                                        文献标识码：A                                  文章编号：1006-4311（2019）34-0197-03

0  引言

降水是区域水资源的主要补给方式，降水量是衡量一个地区水资源丰枯的主要指标。降水量的年际变化趋势直接制约着区域社会经济发展和生态生活环境，影响着区域水资源的调配管理。近年来随着水资源问题的凸显，研究区域性降水量变化特征和寻求对降水量的准确预测技术已成为水资源合理调配的主要研究内容之一。黄显峰等建立时间序列分解预测模型，分别对趋势项和周期项进行检验和提取，利用自回归模型人工合成新的序列对平稳随机项进行模拟和预测[1]。刘银迪等将序位理论引入集对分析建模中，改进集对分析预测模型，提出了一种基于序位的集对分析降雨量预测模型[2]。奚立平等以无为县为研究区域，利用1957～2016年降水量资料，采用时间序列分析的方法，研究了降水量预测模型[3]。赵国超等基于极限学习机 ELM模型、BP神经网络模型和广义回归神经网络GRNN模型建立了降雨预测模型[4]。金冶利用ARIMA模型对丹东市降雨序列进行研究，建立了预测模型[5]。对于降水中长期预测的成果较多，方法也趋于成熟，其中ARIMA模型采用随机样本数据系列构建降水回归模型，在许多区域降水预测中得到应用，应用效果较好[6-8]。ARIMA方法是国内较为流行且有效的单一时间序列预测模型，该模型优点为短期预测精度较高。本文采用ARIMA模型对渭南市历史降水量趋势进行模拟分析，建立最优降水量预测模型，对近5年降水趋势进行预测并与实际降水量进行对比分析，以验证模型的可行性和适用性。

1  研究区域

渭南市地处东经108°50′-110°38′和北纬34°13′-35°52′之间，位于黄河中游，陕西关中渭河平原东部，是陕西省的“东大门”。此地属暖温带大陆性季风型半湿润气候，四季分明，光照充足，雨量适宜。春季气候多变，夏季炎热多雨，秋季凉风送爽，冬季晴冷干燥，年均气温12-14℃，年雨量600毫米左右。气候条件优越，有利于发展农业，但伏旱、秋涝和夏季干热风对农作物造成的危害较大。对渭南市的降水时空变化规律和短期预测方法进行研究可为此区域农业高效用水提供科学依据，具有重要的社会意义。

2  资料与方法

2.1 资料来源

研究原始数据来源于中国气象数据网。对渭南市华山站1953～2018年的月降水量进行统计得到渭南市近66年的年降水量，其中1953～2013年的年降水量作为趋势预测模型的参数优选数据源，2014～2018年的降水量用于预测模型的检验与分析。

2.2 ARIMA模型

ARIMA模型全称为自回归积分滑动平均模型，是最常见的一种用来进行时间序列预测的模型。年降水量是随时间发生变化的随机序列，借助BIC准则判定ARIMA模型中（p，q）的最佳值，构建降水回归模型，主要结合三变量方法进行回归预测，回归模型方程为：

3  模型构建与分析

3.1 数据处理

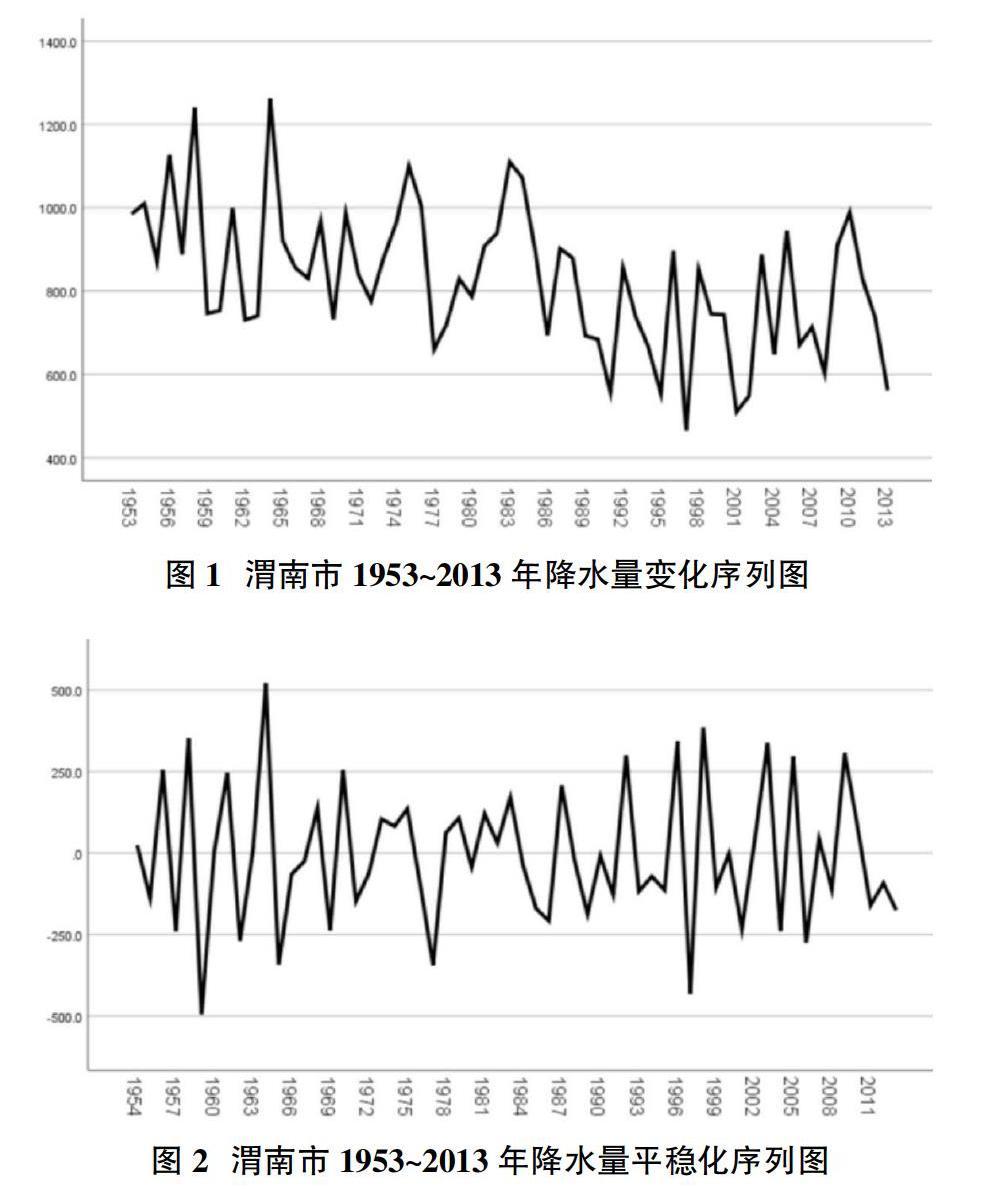
运用SPSS 25软件对渭南市1953～2013年连续61年的年降水量进行数据序列图绘制，如图1所示。从图1可以看出，1953～2013年渭南市年降水量呈波状变化，整体而言随着时间的推移渭南市年降水量呈下降趋势。初步判定年降水量序列为非平稳序列，需要进行平稳化处理。

对渭南市年降水量样本数据作一阶差分，差分后的序列图如图2所示。由图2可见平稳化处理后序列在均值两侧一定范围内波动，此时得到的序列视为平稳化序列。

3.2 模型参数率定

進一步确定模型参数，确定自回归模型的自回归阶数 p、差分次数d、移动平均项q，进行月降水量的自相关和偏相关分析，见图3。

从图3可以看出，渭南市年降水量数据序列经过一阶差分处理后自相关系数递减到零速度较缓慢，当k取1阶时，月降水量的自相关与偏相关处在置信区间外，不太显著，随k增大，ACF、PACF逐渐趋近0，呈现拖尾特征。根据BIC最小为理想阶准则，经过多次模拟分析最终得到较优的模型ARIMA（1，1，1）。对渭南市1958-2013年的年降水量进行模拟，并对模拟值与真实值进行拟合及残差序列分析，见图4和图5。

由图4和图5可见残差序列在均值0上下置信区间内，残差序列通过了白噪声检验，认为残差序列为白噪声序列，模型拟合效果比较好。通过参数评估，可得渭南市年降雨量预测模型如下：

3.3 模型适用性检验及拟合

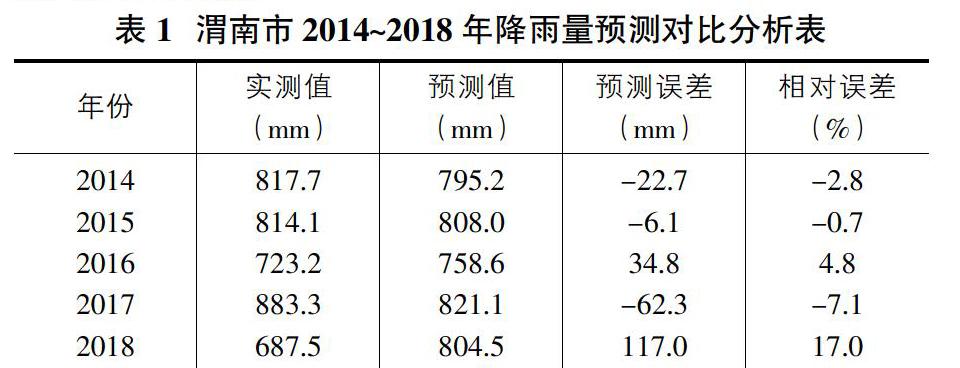
使用预测模型对1953～2013年降水量数据进行拟合，实测降雨量与模拟降雨量序列图如图6所示，拟合残差自相关与偏自相关图如图4和图5所示。由图6可知，此模型对历史数据的拟合度较高，拟合序列与实测序列的变化趋势完全一致。对2014～2018年降水量数据进行模拟，5年降雨量实际值与拟合值的分析结果见表1。

从预测结果对比可以发现，ARIMA模型2014-2018年降水量的预测值与真实值差异较小，4年相对误差均在10%内，得到的预测结果均在置信区间内，仅2018年的相对误差超过10%，分析其原因为随着预测期延长，预测序列趋势变化出现偏差，致使预测精度降低。总体而言预测值的年度变化趋势与实际降水趋势比较一致，能够较好地反映降水量的年际变化，可以较好地进行短期的降水量预测与趋势分析。

4  结论

根据以上建模结果，发现ARIMA模型能够比较好的预测分析，挖掘渭南市降水序列的变化规律。从拟合的结果还可以看出渭南市近些年降雨量呈现略微下降的趋势，随着预测期的延长，预测精度降低。在使用ARIMA模型预测年降雨量时，尽量保证数据序列足够的情况下，采用逐年实时校正的预测方法，进行中短期降雨量预测，避免预测期过长引起预测偏差增大。

参考文献：

[1]黄显峰，邵东国，等.降雨时间序列分解预测模型及应用[J].中国农村水利水电，2007（09）：6-8.

[2]刘银迪，张小壮，等.序列集对分析在辽河流域年降雨预测中的应用[J].安徽农业科学，2011（28）：17534-17536.

[3]奚立平，蔡文庆，等.基于时间序列分析的无为县降水量预测模型的研究[J].安徽水利水电职业技术学院院报，2018（01）：50-53.

[4]赵国超，赵鹏飞，等.天津市降雨时空分布特征及预测模型研究[J].海河水利，2019（04）：41-43.

[5]金冶.基于ARIMA模型的丹东市降雨时间序列分析[J].水利规划与设计，2017（05）：35-37.

[6]刘剑.基于ARIMA模型在降水量趋势分析与预测中的应用[J].水利科技与经济，2018（9）：67-69.

[7]李楠.Logistic-ARIMA预测模型在城市水资源需求导向及优化配置中的应用分析[J].地下水，2017（04）：137-139.

[8]张忠国.基于ARIMA与ANN组合模型的需水量预测方法研究[J].地下水，2015，37（06）：95-97.