基于WPT和t-SNE的直升机桨叶损伤特征提取

曲怡霖 陈仁文 吕宏政 叶杨

南京航空航天大学 机械结构力学及控制国家重点实验室，江苏南京 210016

一、引言

复合材料桨叶是直升机的核心部件之一，在机体振动和复杂气动环境作用下，时常发生基体开裂、分层、拉丝断裂、穿孔等损伤[1]，为飞行安全埋下巨大的隐患。实时监测桨叶的健康状况，判别可能发生的故障和损伤，对实现故障预警、确定损伤修复方案至关重要。

小波包变换（Wavelet Packet Transform，WPT）因能对信号的高频部分进一步分解，在信号处理、故障诊断与监测领域得到广泛应用[2-4]，已经有学者将其结合神经网络实现了直升机桨叶的损伤识别[5]。但是，更为精细的频段划分会导致WPT得到的特征维数激增，严重降低计算效率，且存在的冗余特征可能会对损伤判别造成干扰，故深入挖掘出损伤敏感特征十分必要。流形学习可以从高维空间恢复低维流形，实现维数约简，常见算法有局部线性嵌入（Locally Linear Embedding，LLE）、等距特征映射（Isometric Feature Mapping，Isomap）、局部切空间排列（Local Tangent Space Alignment，LTSA）、Sammon映射（Sammon Mapping）、局部保留投影（Locality Preserving Projections，LPP）等，这些方法在常见机械的故障诊断中应用广泛[6-11]。而t-分布随机近邻嵌入算法（t-Distributed Stochastic Neighbor Embedding，t-SNE）[12]提出后，因其卓越的可视化降维效果而得到各方学者的重视[13-14]。

针对研究现状，本文提出了一种基于小波包能量和t-SNE的桨叶损伤特征提取新方法。利用WPT提取桨叶振动响应信号中的损伤特征后，依据t-SNE算法挖掘小波包能量特征的低维流形，将降维结果输入K最近邻（K-Nearest Neighbor，KNN）分类器中，验证所提取特征的有效性。验证结果表明，这种方法能有效提高桨叶损伤识别的准确率。

二、小波包分解和特征提取

直升机桨叶在服役过程中受力复杂，会产生含有大量高频成分的非平稳信号。正交小波变换只能对信号低频部分进一步分解，而小波包变换还增加了对信号高频部分的分解，有利于准确提取敏感特征，实现损伤桨叶的识别和评估。

由公式（1）定义的小波包{un(t)}是包括尺度函数u0(t)=φ(t)和母小波函数u1(t)=ψ(t)在内的函数集合。h(k)、g(k)分别为低通滤波器系数和高通滤波器系数。

小波包分解是利用母小波函数ψ(t)和与其相应的尺度函数φ(t)组成的正交镜像滤波器组，将振动信号分解为某尺度下的低频成分和高频成分，改变尺度，继续对低频和高频成分进行分解，直至达到所需要的频率分辨率的过程。图1为三层小波包分解示意图，共生成8个节点，每个节点的带宽占整个频段的1/8。

小波包变换的分解系数为：

式中：dj,n—第j层n节点的小波系数；

dj+1,2n、dj+1,2n+1—第j+1层2n节点和2n+1节点的小波系数；

m —小波系数的个数。由式（3）求得由节点频带能量所组成的原始高维特征向量：

三、t-SNE流形学习算法

假设一种低维流形结构可以嵌入到高维空间形成高维数据，流形学习就是将高维数据映射回低维空间，揭示数据内在规律，实现维数约简的过程。t-SNE是在随机近邻嵌入（Stochastic Neighbor Embedding，SNE）算法的基础上演变而来的。SNE算法将欧式距离（Euclidean Distance）换成条件概率来描述两点的相似程度，分别构建高维空间、低维空间数据的概率分布，应用KL距离（Kullback-Leibler Divergence）衡量两个分布之间的相似性，运用梯度下降法求解代价函数的最小值。针对SNE算法中不同簇边界模糊和KL散度不对称的缺点，t-SNE通过引入t分布代替正态分布解决了拥挤问题，应用联合概率分布简化梯度公式解决了不对称问题。

使用t-SNE将高维空间的数据集合X={x1, x2,…,xn}映射到低维空间数据集合Y(T)={y1, y2,…,yn}的算法步骤如下：

（1）困惑度为近邻的数量，当其确定时，按如下公式计算两个高维空间数据点xi和xj的条件概率；

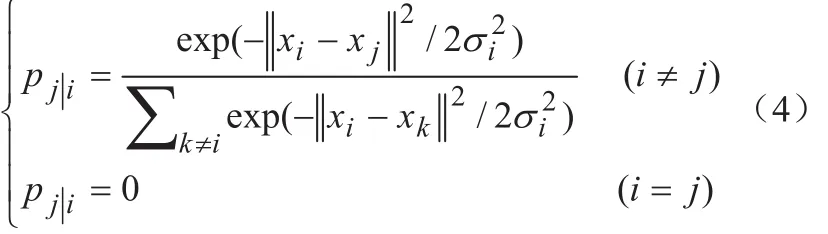
其中，σi—以xi为中心点的正态分布的方差。

（3）按如下公式计算低维映射的联合概率分布；

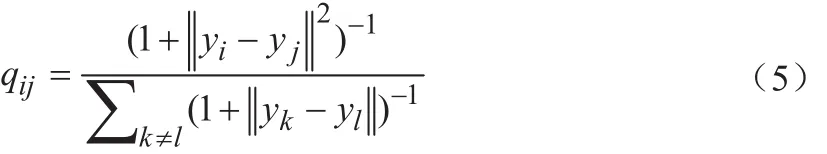
（4）根据公式（6）计算代价函数对yi的梯度公式：

其中，C—两个联合概率分布P和Q之间的KL散度。

（5）根据公式（7）获得低维映射的数据；

其中，η—学习率；

α(t) —动量。

（6）将步骤（3）～（5）迭代T次，获得低维空间完整的数据集合。

四、桨叶损伤识别实验验证

预制的复合材料桨叶长为800mm，弦长600mm，剖面选用NACA0015翼型，由C型大梁、蒙皮、配重铅条、泡沫芯和后缘条五个部分组成。为了实现对直升机桨叶的损伤识别，根据桨叶常见的损伤类型制作了如图2所示的穿孔、分层、基体开裂和拉丝断裂的桨叶。材料和几何尺寸相同，损伤类型和损伤程度不同的6片桨叶的详细损伤参数如表1所示。超声波、声发射和红外线检测等方法产生的激励信号很容易被直升机强大的背景噪声所淹没，故可利用机体振动本身作为激励，通过分析桨叶的振动信号来实现损伤判别。实验室环境下，利用振动台模拟直升机在服役时的真实振动，作用于桨叶获得输出响应，对比不同的高维特征选取方法和降维方法，获得提取损伤特征的最佳方案。具体的损伤检测过程如图3所示。

表1 桨叶损伤参数

搭建如图4所示的实验台系统，选用PCB公司的压电加速度传感器333B42来测量纵向加速度，用胶水粘贴在距桨叶固端200mm的位置处，将传感器接收的模拟信号经模数转换模块AD7606处理后传送到计算机。根据奈奎斯特采样定理和桨叶固有频率设定采样频率为8000Hz，信号长度为5000。每种桨叶采集200组数据，6种桨叶共采集1200组数据。

1、小波包能量特征提取

原始高维特征提取对准确识别桨叶损伤状态至关重要。目前，联合时-频分析的特征提取方法得到了广泛应用。但有学者指出不同时、频域指标对准确实现损伤识别的贡献不同[15]，对于不同的研究对象，最优特征参数的选取也大不相同。因此，本文在提取原始特征时对比了小波包能量特征和时频混合特征，从而筛选出具有较好规律性和分辨率的原始特征参数。

为了获得较高的频率分辨率，对6种桨叶的振动信号进行8层小波包分解，将全频段均匀划分成256个子频带，子频带的频率分辨率为15.625Hz。以香农熵为代价函数选择最优小波基，计算公式如下：

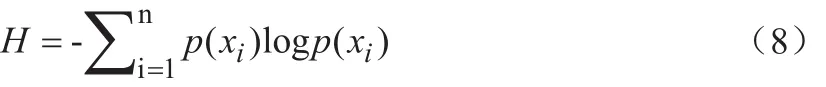
最终从100个候选的母小波中选定熵值最小的db41小波对振动信号进行分解，形成小波包能量特征矩阵R1200×256。在小波包能量特征矩阵的基础上，融合平均值、峭度、均方根、峰值因子、脉冲因子、裕度、偏斜度、方差8种时域参数，组成了时频域混合的原始特征矩阵 R'1200×264。

2、流形学习降维

为了对比不同降维方法的特征提取效果，分别用线性降维算法主成分分析（Principal Component Analysis，PCA）、 流 形 学 习 算 法 LLE、Isomap、LLP、t-SNE、SNE、LTSA、Hessian局部线性嵌入（Hessian Locally Linear Embedding，HLLE）和Sammon Mapping对原始特征矩阵进行维数约简。发现运用流形学习的经典算法LLE、Isomap和LLP时会发生严重的数据丢失，无法进行二次特征提取。将嵌入维数设置为3，其他算法的降维效果如图5所示，t-SNE算法的困惑度选用默认值30。

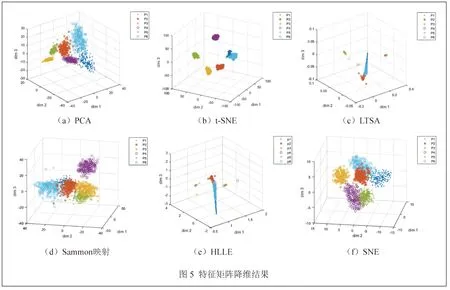
图5（a）的PCA降维聚类效果良好，只有健康桨叶和拉丝断裂桨叶发生了轻微混叠，基本上能够区分。图5（c）和图5（e）分别采用了流形学习的LTSA和HLLE方法，极大地减小了类内间距，聚类效果优于PCA，但P1和P2均发生了混叠。图5（d）Sammon映射和图5（f）SNE方法基本上可以分离不同情况的损伤，但类内间距较大，且不同类别的边界之间混叠严重。图5（b）t-SNE的分类效果明显优于流形学习的其他方法，不仅在很大程度上缩小了类内间距，增大了类间距，而且几乎没有发生混叠，凸显出用t-SNE算法进行敏感特征提取的优越性。

3、桨叶健康状态评估

分别用PCA、LTSA、SNE、HLLE、t-SNE和Sammon映射6种降维方法将两个原始高维特征矩阵的维数降至3维，同时把降维结果输入到KNN分类器，对比不同特征选取和降维方法的分类准确率。将1200个数据样本按照3:1的比例分成训练样本和测试样本，即用900个样本来训练模型，300个样本来测试模型的准确率。测试结果如表2所示，分类器的近邻因子设置为5。

表2 桨叶的损伤识别准确率（%）

结果显示，小波包能量作为原始高维特征的识别效果总体上优于时频混合特征，表明选用时域指标作为特征参数的识别效果较差，不能很好地揭示出桨叶的损伤特征。相较于其他降维方法，t-SNE算法的识别准确率为最高的98.67%，只有P1正常桨叶和P6拉丝断裂桨叶发生了误判，并且对两种高维特征矩阵有相同的识别率。这不仅说明小波包能量作为原始特征具有完备性，又说明t-SNE算法具有降噪效果，能剔除不利于损伤识别的特征参数，提升桨叶损伤识别的准确率。

t-SNE算法中嵌入维数和困惑度的选取可能会影响分类结果，为获得最佳识别率，对比了6种桨叶在不同嵌入维数和困惑度下识别率的平均值。发现识别准确率不随嵌入维数的变化而变化，即使维数降至2维甚至1维时，识别准确率仍高达98.67%，不同困惑度下的辨识率如图6所示，当困惑度大于10，达到最佳识别率98.67%。可见在提取桨叶损伤特征的过程中较容易达到最佳分类效果。

五、结论

为了在线监测、判别桨叶的损伤状况，本文提出了一种基于小波包和t-SNE的损伤特征提取方法，开展了模拟服役状态下的振动实验，研究结果表明：

（1）利用小波包对桨叶振动信号进行分解，提取子频带能量为高维特征矩阵，能准确反映桨叶的健康状况，为实现损伤诊断奠定了基础；

（2）流形学习中的t-SNE算法可以对特征矩阵进行降维处理，得到能揭示高维数据内在规律的本质结构特征。相较于LTSA、Sammon映射、HLLE、SNE、PCA等方法，t-SNE在改善可视化效果的同时，还提高了损伤识别的准确率，而且识别率几乎不受嵌入维数和参数选择的制约；

（3）实验室环境下，融合了小波包和t-SNE的损伤特征提取方法可以识别不同损伤类型、不同损伤程度的桨叶，实现了桨叶健康状态的在线监测和诊断，但还有待于在工程实践中深入验证。