基于Voronoi图理论的微体积成形数值建模及验证

席道英郑伟

(山东建筑大学工程力学研究所，山东济南250101)

0 引言

随着科学技术的快速发展，人们对微型零件的需求正逐渐增加，微塑性成形技术成为材料加工领域的研究热点。微塑性成形技术是指通过材料发生一定的形变，制造出二维或三维方向上尺寸＜1 mm零件的技术[1-4]，具有高生产效率、性能好、误差小及无污染等优点。微塑成形技术在微机械及微电子等领域具有十分重要的应用前景，近几十年在市场因素的推动下迅速发展成为材料加工领域的热点。

数值模拟方法是研究微塑性成形的主要手段之一，在生产工艺中，可以减少工艺设计的时间和降低生产成本。目前提出的微塑性成形理论中的区域化模型不包含各种尺度参数，因此基于成形理论的数值模拟不能直接使用现有的有限元软件。很多学者都基于实验数据推导本构关系及研究微塑性成形过程中的尺度效应现象，但缺少一些理论依据[5-6]。彭林法[7]考虑了表面层模型理论的情况，将表面层晶粒看作单晶，从而改进了Hall-Petch公式，建立了一种复合材料区域化模型并实现了微塑性成形过程的数值模拟。但在微尺度下，变形区域只有几个或十几个晶粒时，不能忽视单个晶粒取向对整个变形的影响，因此需要对整个材料模型进行晶粒化处理，以便更清晰地实现对微塑性成形过程的数值模拟分析。常妍妍[8]在研究微成形工艺时引用一种新的数值模拟方法，将所用的多晶体材料看作由正六边形组成的晶粒，每个晶粒代表一个特殊作用的有限单元，其每个晶粒单元由晶粒边界单元连接，这些晶粒边界单元用来描述晶粒之间的剪切变形。王广春等[9]将模型中的每个晶粒单元视为由6个节点组成，在具体的网格划分中将其分为2个四边形单元。将该模型引入到研究激光微拉深和胀形的过程中，虽然模型有局限性，但为在连续介质力学框架下有限元模拟微塑性成形提供了有效的建模思路。Zheng等[10]利用二维Voronoi多晶简化模型数值研究了微成形过程中试样晶粒分布对摩擦行为的影响，为后来建立基于Voronoi图的三维多晶模型奠定了基础。由于二维的多晶模型不能精确地反映晶粒取向分布不同对微塑性成形过程中摩擦因子和流动应力的影响，因此建立三维的多晶几何模型并进行数值模拟，可以更清晰地反映变形过程中的尺寸效应现象。Jiang等[11]基于Voronoi图理论建立了一种适用于微尺度下塑性成形的材料多晶模型，在此模型中每个晶粒的材料流动应力与晶粒的尺寸和成形温度有关。此外，考虑晶界强化作用并简化晶粒为立方体，提出了一种多晶几何模型，从而实现了微尺度下镦粗过程的数值模拟[12]。

文章研究尺寸为微尺度，不能忽视坯料中单个晶粒取向对整个变形的影响，因此基于Voronoi图理论，建立考虑表面层理论的三维几何模型，根据各个晶粒的取向不同，将区域分为3类，赋予其不同的本构关系，得到三维材料本构模型。利用有限元软件ABAQUS实现微镦粗过程的数值模拟，得到的流动应力结果与实验数据相对比，以验证该模型的可行性。

1 微尺度下基于Voronoi图的数值模型建立

1.1 多晶几何模型的建立

在三维空间中，过去很多研究学者一般在多晶体模型中以六面体单元代表晶粒，但模拟结果不能准确地反映晶粒的形状不规则性和对材料变形过程的影响，因此并不是最好的模型选择。研究发现，Voronoi图从种子点生成六边形的过程与真实多晶体材料的结晶过程具有一定的相似性[13-14]。基于Voronoi图理论在有限元软件ABAUQS中建立三维多晶几何模型的具体过程如下:

(1)通过第三方软件MATLAB，在Mpt工具箱中生成多晶体内所有晶粒表示点的几何信息。

(2)将多晶体中的每个晶粒所包含点的几何信息与周围其他晶粒相交，得到共同的几何信息集合。若结果≥3个点，则得到了晶粒每个面所包含点的几何信息；若结果为2个点，则得到了晶粒每个面所包含边的信息。再将多晶体中晶粒所包含面和边的全部几何信息按照格式一并输出为txt文本并保存。

(3)Python作为ABAQUS/CAE的脚本语言，可以实现模型的前处理过程。通过ABAQUS的脚本接口读取 MATLAB中生成的数据，通过WirePloyLine命令自动生成晶粒每个面的边，用AddFaces命令将晶粒的边生成面。

(4)在Assembly模块中将晶粒的面通过布尔运算生成晶粒的壳，然后选中生成的壳和实体进行移动到重合，再利用Assembly模块中cut geometry功能，通过生成晶粒的壳和目标实体可得到任意形状的多晶几何模型。

文章主要以圆柱体来建立材料多晶模型，如图1所示。

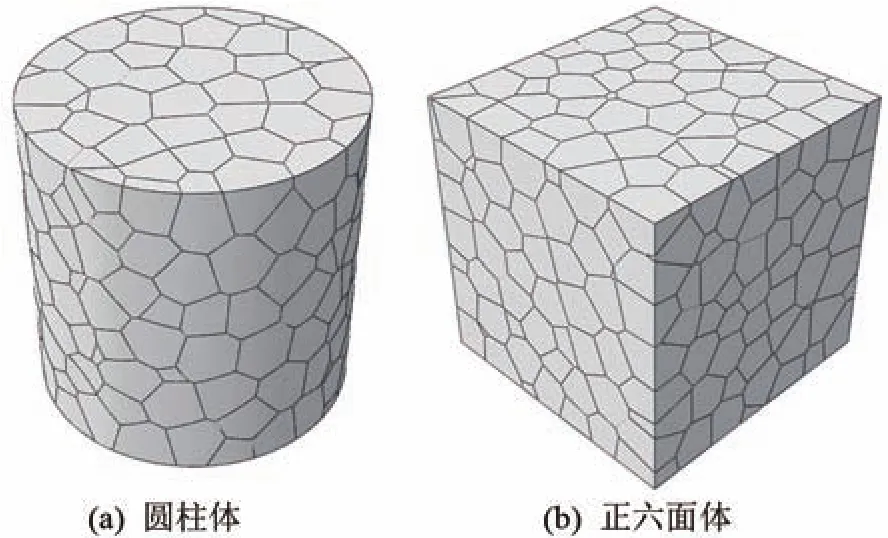
图1 基于Voronoi图理论的三维多晶几何模型图

1.2 区域化本构模型的建立

与单晶体相比，受位错塞积影响的多晶体的晶粒在塑性变形过程中会在晶界附近产生很大的应力场[15]。其中，多晶体中的晶粒遵循Hall-Petch公式，由式(1)表示为

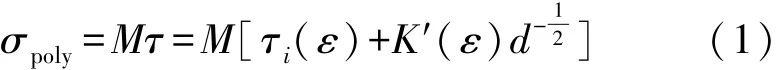
式中:σpoly为多晶体变形中的流动应力，MPa；M为多晶体晶粒的取向因子；τ为塑性变形中的总应力，MPa；τi为沿滑移面滑动时产生的摩擦切应力，MPa；ε为塑性变形中的应变；为晶界附近由于位错塞积对位错运动所产生的抵抗切应力，MPa；d为平均晶粒尺寸，μm。考虑塑性变形过程中的硬化作用，K′和τi都是应变的函数。

由于传统的多晶体包含晶粒数量非常大，单个晶粒对整个变形的影响可忽略，取其各个晶粒取向因子的平均值，对于面心立方晶格的多晶体，内部晶粒取向因子的平均值为3.06。然而在微尺度下，变形区域只有几个或十几个晶粒，单个晶粒取向对整个变形的影响作用不能忽视。Huang[15]对多晶铜拉伸试样的显微组织进行了分析。在纯铜试样的模拟中，每个三维模型均由上百个晶粒组成，可以根据二维的图像反映三维空间晶粒的分布。根据在三维空间的不同取向分布，将晶粒大致分为3大类，如图2所示。第1类晶粒主要分布在反极图三角形的中间部分，以[411]为代表；第 2类晶粒大致分布在[100]周围15°内，并以[100]为代表；第3类晶粒分布在[111]周围20°内，作为[111]类型。课题组前期对纯铜试样晶粒位向分布进行了测试[16]，电子背散射衍射技术测试的结果如图3所示。

从知识产权评议在我国十余年的实践来看，其所承载的功能不断丰富和拓展：一方面，知识产权评议的目的从单纯的防范重大经济科技活动的知识产权风险，逐渐延伸至优化政府经济科技决策和政府管制；另一方面，知识产权评议的适用范围从具体的经济科技活动（初期主要针对政府投资项目），逐渐扩展至产业发展、科技进步、国际投资和国际贸易等领域的政策制定、政策实施与宏观层面的经济科技决策。

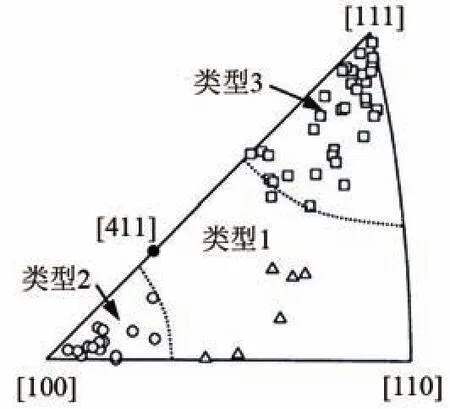
图2 变形方向上纯铜晶粒取向的分布图[15]

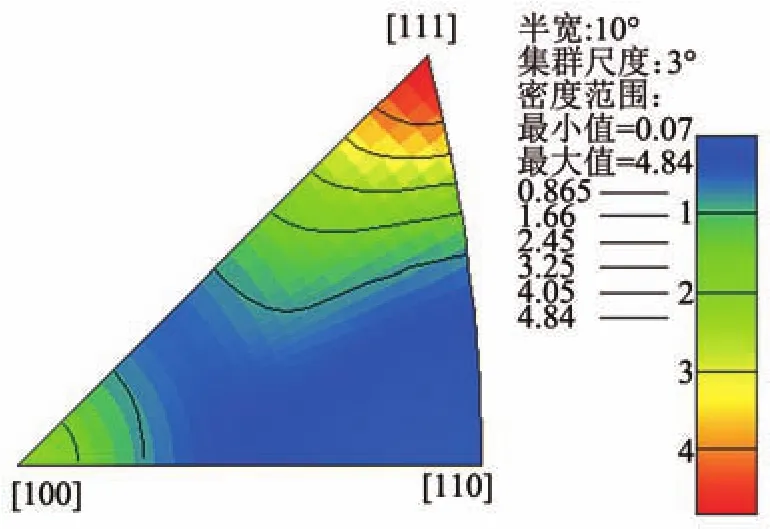
图3 前期测得纯铜试样电子背散射衍射反极图

为了研究多晶与单晶纯铜塑性变形行为的相关性，Huang等[15]分别将取向平行于[411]、[100]和[111]的晶粒作为面心立方多晶中出现的3种类型晶粒的代表，其取向因子M和体积分数f见表1。

表1 3种不同类型晶粒的取向因子M及体积分数f表[15]

在连续介质力学理论的框架下，考虑到微塑性成形的变形机理，需要对建立的有限元多晶模型做以下假设:

(1)表面层晶粒的位错可以在外应力作用下沿最有利滑移系统滑移，其取向因子M为2。

(2)在变形方向上，只有[411]和[100]及[111]3种具有代表性取向的晶粒属于不存在自由表面的内部晶粒，建模过程中3种晶粒按照1∶2∶7的比例进行分配。

(3)在变形过程中不考虑晶粒转动。

简化流动应力仅为应变的幂指数，对文献[1]给出的CuZn15单向压缩实验数据进行回归分析，求解得到Hall-Petch公式中的待定系数，由式(2)表示为在变形方向上，不同取向晶粒的流动应力应变曲线如图4所示。3种类型的代表晶粒的流动应力都大于表面层晶粒，[111]方向上的晶粒的流动应力最大。可以用表面层模型理论解释:在试样微小的情况下，表面层的晶粒相对较多，在试样变形时，与内部的各种类型晶粒比较，表面层晶粒受到的约束较小，在较低的流动应力下就能发生变形，由此可得，微塑性成形中试样的流动应力随尺寸的减小而减小。根据这些应力—应变数据可以定义在三维多晶模型的属性上，使其进行数值模拟分析。

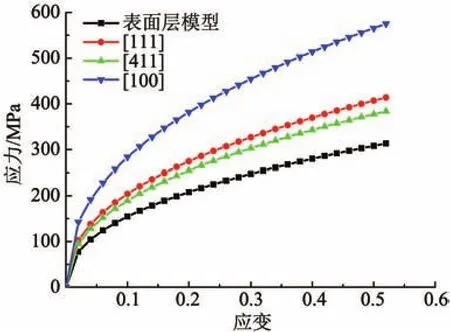
图4 不同取向晶粒的流动应力—应变曲线图

2 微体积成型的模拟及验证

根据晶粒取向分布的体积分数，随机生成了3种不同晶粒取向分布的有限单元法模型(分别为模型1、模型2和模型3)。压缩后3个模型剖面变形结果如图6所示。在3种不同晶粒取向的多晶模型中，2侧均出现了不同程度的凹凸不平，这与实验结果相吻合。其产生原因为:由于随着试样尺寸的减小，试样中包含的晶粒个数也随之减小，晶粒与晶粒之间由于晶粒取向的差异引起的力学性能的差异也愈加明显，最终造成了试样在变形过程中的不均匀性。

通过模拟结果及流动应力—应变关系可以得到3种不同晶粒取向随机生成的多晶模型的应力—应变曲线，如图7所示。在微镦粗的过程中，由于尺寸发生微小的变化，材料产生了明显的尺寸效应。由于晶粒的分布和取向不同，最终由3种有限单元法模型得到的流动应力也有所不同。相同应变下，模型1的流动应力较大，但三者相差不大，最大相差为4.33%。

图5 微尺度下试样单向压缩的模拟过程图

图6 不同晶粒取向分布的有限单元法模型的剖面变形图

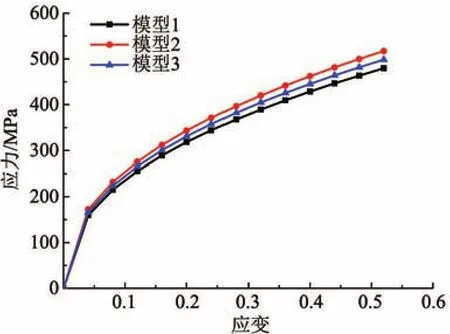
图7 由3种有限单元法模型得到的应力—应变关系图

将3种FEM模型模拟得到的流动应力的平均值与文献[1]中的实验结果进行对比，如图8所示。模拟得到的流动应力要略高于实验中得到的流动应力，分析认为是受模拟过程中选取的[111]取向的晶粒的影响，其加工硬化率要高于其他取向的晶粒，造成模拟结果中内部多晶的流动应力要高于实际情况。因此，所建立的三维有限元模型具有一定的可行性，能够准确地反映微镦粗过程中的尺寸效应现象。

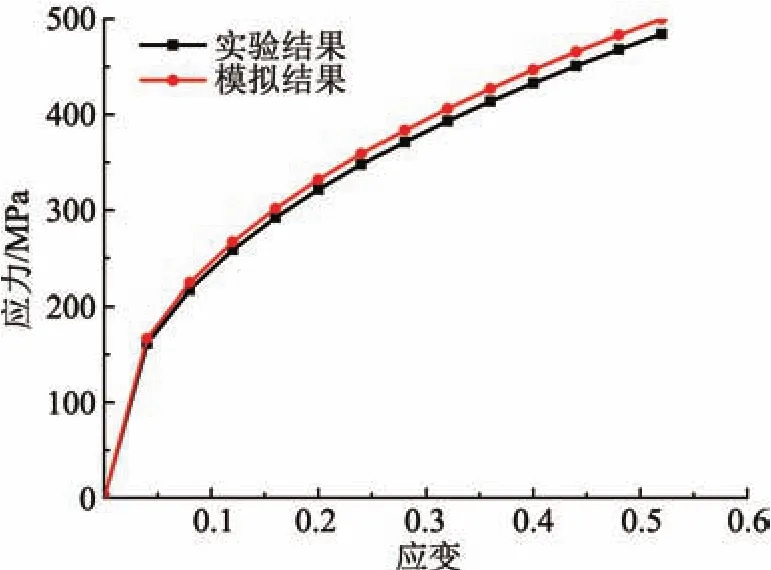
图8 模拟结果与实验结果的对比图

3 结论

通过研究，得到以下结论:

(1)基于Voronoi图理论，在ABAQUS中生成了圆柱体和立方体的三维多晶几何模型，能够更真实地反映试样的晶粒形状，修正了宏观的Hall-Petch公式，得到了微尺度下的有限元多晶模型，证实了尺寸效应现象及表面层晶粒的流动应力小于内部晶粒。

(2)通过对三维有限元模型进行微镦粗过程的数值模拟，晶粒分布不同对变形后的形貌产生不同的结果。数值模拟的数据与实验的结果相吻合，实现了实验与模拟的一致性，验证了三维多晶几何模型和本构模型的可行性。并且，此建模方法能更广泛地分析微塑性成形中尺寸效应现象。