隧道应力扰动区及其影响因素分析

何洵，李铀

隧道应力扰动区及其影响因素分析

何洵，李铀

(中南大学 土木工程学院，湖南 长沙 410075)

一般认为扰动区范围为隧道截面最大直线尺寸的3~5倍。在弹性状态下进行分析，利用已有的未考虑自重的圆形隧道解析解确定圆形隧道扰动区影响因素及扰动区范围，并总结出圆形隧道扰动区半径与隧道半径和泊松比之间的多项式关系。采用ANSYS分析考虑自重的圆形、直墙半圆拱和矩形3种截面隧道开挖后围岩应力场和扰动区范围。应用弹塑性折线理论将弹性状态所得的成果推广至弹塑性状态。研究结果表明：圆形、矩形、直墙半圆拱3种截面形式的最大扰动区范围均超出了隧道截面最大直线尺寸的5倍，即一般情况下大于现时认为的3~5倍；从减小扰动区范围的角度出发，相同高度与跨度的3种隧道截面，圆形截面最优，直墙半圆拱截面次之，矩形截面最差。研究成果可为隧道支护设计以及数值模型计算域的选取提供参考。

圆形隧道；围岩；应力扰动区；数值模拟；弹塑性分析

地下洞室开挖将引起应力重分布，开挖后巷道周围应力发生显著变化，而远场应力基本保持不变。通常认为开挖前后应力变化小于5%的区域没有受到开挖影响，并称这一区域的岩体为原岩；而变化大于5%的区域是开挖影响区，并称为扰动 区[1]。目前，扰动区范围一般认为是“井巷或采场最大直线尺寸的3~5倍”，对隧道而言，就是隧道横截面最大直线尺寸(后面简称为隧道最大直线尺寸)的3~5倍。扰动区范围直接影响隧道稳定性分析和支护设计，众多学者在这方面进行了研究。周辉等[2]研究了深井巷道围岩扰动应力场与开挖扰动区之间的关系。并且利用 FLAC3D进行数值模拟分析，得到了水平应力、垂直应力、最大主应力、最小主应力的变化规律与相互之间的联系，分析了深井巷道掘进过程中围岩扰动应力场的演化特征。赵维生[3]等对垂直交岔点围岩稳定性以及开挖扰动后围岩主应力展开研究，结果表明扰动后主应力主要受到原岩应力的影响，而基本不受交岔点与地应力空间位置和巷道开挖顺序的影响。唐礼忠等[4]针对冬瓜山铜矿深部出矿巷道其复杂的赋存条件和“高应力+动力扰动”的应力环境，利用ABAQUS得到动力扰动后围岩应力场及塑性区，并且提出了多种工况下的支护优化方案。刘新颖等[5]对高渗透压下围岩稳定性进行分析，得到了围岩开挖后应力场以及位移场分布特征和开挖卸载对渗流场的影响。董春亮等[6]研究了深部圆形巷道开挖卸荷的围岩力学特征及破坏机理。得到开挖卸荷下的围岩应力场特征为为最小主应力卸荷、最大主应力集中，而主应力差的瞬间增大，从而使得围岩裂隙扩展，形成连续分布的破坏区。传统塑性力学在围岩应力与变形的求解过程中，将引入Mohr-Coulomb或Hoek- Brown等屈服准则[7−11]。然而，屈服准则的选用不同，得到的应力场结果也将出现差异，这种不确定性将导致围岩应力场与实际情况不相符[12−14]。弹塑性折线理论可以避开屈服准则的影响，确定两类边界条件下弹塑性问题的准确应力场，取得了如下重大成果：当边界条件全为应力边界条件，或有位移边界条件但在塑性区边界上仅有零位移边界条件(对应力边界条件没限制)时，塑性力学问题的应力场表达式完全等同于把所讨论问题当成弹性问题求解所获得的应力场表达式[15−17]，这为隧道开挖进入弹塑性状态后围岩的扰动分析奠定了理论基础。李铀等[14]应用弹塑性折线理论所得应力场新成果对圆形巷道的扰动区和围岩的临界破坏深度进行了研究，分析表明扰动区半径与外载的大小与作用形式、泊松比和埋深有关，有时会远远超出隧道最大直线尺寸的3~5倍。本文首先将以弹性力学为基础，先利用已有的未考虑自重影响的圆形隧道解析解进一步分析扰动区范围，确定扰动区影响因素，并采用ANSYS得到考虑自重的开挖扰动后围岩应力场，通过分析得到扰动区大小。然后应用弹塑性折线理论将弹性状态所得的成果推广至弹塑性状态，研究成果将为隧道开挖数值模拟以及支护设计提供依据。

2 弹性状态圆形隧道扰动区及影响因素分析

如图1圆形隧道受力模型所示，以隧道中心为原点建立坐标系，水平方向为轴(极坐标系下与极轴重合)，铅垂方向为轴，隧道轴向为轴，其中为扰动区半径与轴的夹角(顺时针为正，下文简称为夹角)，为圆形隧道半径。

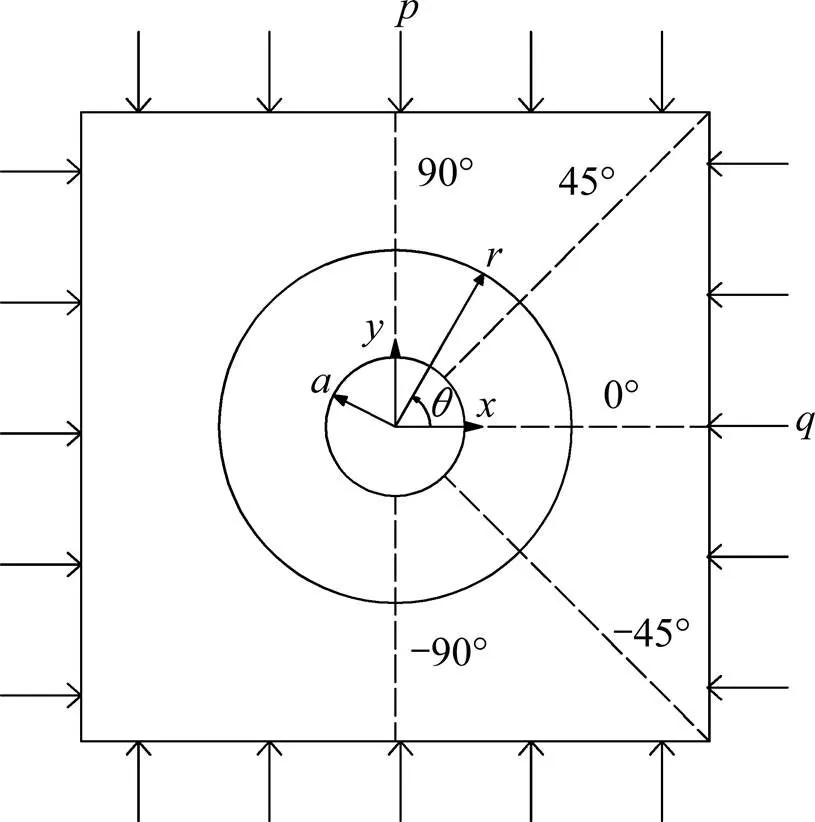
图1 圆形隧道的受力模型

假设地层各向同性且均质，弹性力学已经求得半空间体在自重应力下的应力场[18]，即隧道开挖之前的原岩应力场：

式中：，，分别为地层深度、容重与泊松比。

设隧道开挖的深度为，隧道半径为，此时隧道处于平面应变状态，受力模型如图1所示。由式(1)的解答，可将和近似表示为：

由扰动区定义易知，扰动区范围实质上是应力变化大于5%的区域，因此通过转换使得开挖前后应力处于相同坐标系下，再来研究扰动区范围更为方便。因此先将文献[18]所得图1模型极坐标系下的解答，转换成平面直角坐标系下的解答：

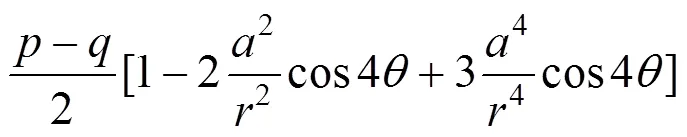
式中：为水平应力；为铅垂应力；为剪应力。

现研究水平应力与铅锤应力来确定扰动区半径，根据定义扰动区半径为

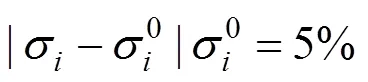
式中：表示扰动后围岩应力；表示原岩应力。

因此对式(3)有：

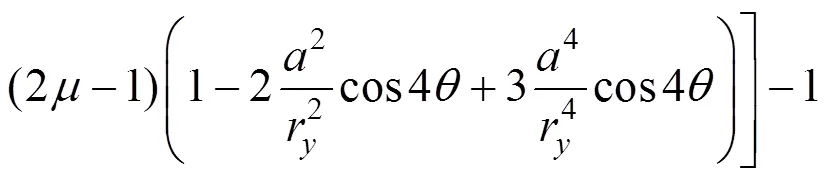
式中：r为水平应力扰动区半径；r为铅垂应力扰动区半径；为r，r与轴之间的夹角。

由式(4)~(6)可得到r和r与泊松比、夹角及隧道半径之间的关系，示于图2，图2中=2 m。

图2 r~θ曲线(a=2 m)

由图2可得扰动区的如下特点：

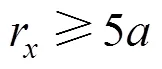
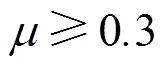
0°方向水平应力：

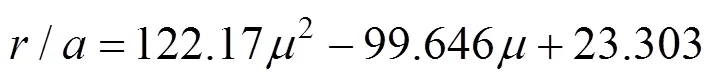
90°方向水平应力：

90°方向铅垂应力：

式(7)~(9)中泊松比为0.1~0.4。式(7)~(9)即可确定扰动区半径的最大值。

上述分析表明，圆形隧道扰动区范围可能超出“井巷或采场最大直线尺寸的3~5倍”这个范围。因此在确定扰动区范围以及数值模型的计算域时应根据具体情况(泊松比、隧道半径、夹角)而定，不然将对围岩应力场和隧道的支护设计产生影响。

2 考虑自重的圆形隧道数值结果及分析

自重对围岩的变形与应力分布有重要影响，上面分析未涉及自重的影响，下面进一步研究自重对圆形隧道扰动区的影响。因考虑自重时，难以获得解析解，下面利用ANSYS数值方法进行研究，计算参数如表1所示。

假设地层是均质且各向同性，开挖扰动后，围岩处于弹性状态。建立弹性状态数值模型如图4所示，为尽可能减小尺寸效应，取较大的数值模型尺寸，为长×宽=120 m×120 m，以圆形隧道圆心为原点建立坐标系，轴即水平轴，轴为铅垂轴，隧道轴线方向为轴。隧道模型上边界采用应力边界，施加均布荷载=(−60)，为隧道圆心埋深。模型左右边界限制水平位移，下边界限制竖向位移，有限元网格见图4。

表1 数值模型计算参数

图4 圆形隧道有限元网格

2.1 有无自重情况下应力场对比分析

图5给出了0°和90°方向最大与最小主应力的分布情况，作为对比，图中也给出了不考虑自重时的计算结果，结果表明：不考虑自重将导致所得主应力数值偏小，这样，应用摩尔−库伦准则来判断围岩的临界破坏区域时，计算结果较不安全，将直接影响到支护设计结果。

2.2 考虑自重情况下扰动区半径分析

考虑自重时扰动区半径如图6所示，从图6 可知：

1) 相对来说，隧道开挖对的影响较小，由确定的扰动区范围均处于隧道最大直线尺寸的5倍以内。

2) 铅垂应力、轴向应力、水平应力共同确定的最大扰动区半径与由主应力确定的最大扰动区半径均在0°与90°方向上，最大扰动区半径为12.5 m，为隧道最大直线尺寸的6.25倍。当泊松比为0.25时，本文第2节中采用式(7)~(9)得到扰动区半径最大值为隧道半径的6.29倍，两者结果相近，这表明单纯确定扰动区范围时，第2节中为简化分析过程，采用水平应力与铅垂应力来确定扰动区范围的可行性。

图5 数值计算域内自重对主应力的影响

3) 在−90°，−45°，0°， 45°，90°方向上，确定的扰动区范围均超过隧道最大直线尺寸的5倍，其它各个方向上为隧道最大直线尺寸的3~5倍以内。

4) 在−90°，−75°，75°，90°方向上，确定的扰动区范围较大，其中90°方向上扰动范围最大，其扰动区半径为12.5 m，为隧道最大直线尺寸的6.25倍；75°方向上扰动区半径为10.88 m，为隧道最大直线尺寸的5.44倍。其他方向上扰动区范围大致为隧道最大直线尺寸的5倍以内。

5) 如图6(b)所示，应该注意的是，在0°和90°方向上，第2主应力扰动区半径均为12.5 m，为隧道最大直线尺寸的6.25倍。这也表明，隧道开挖对第2主应力的影响也是不容忽视的。

通过上面的分析并与不考虑自重的情况对比，可以看出不考虑自重与考虑自重情况对扰动区范围影响不大。

图6 扰动区半径(a=2 m)

2.3 泊松比、洞径与隧道埋深变化对扰动区范围的影响

2.3.1 泊松比变化对扰动区范围的影响

仍采用图4所示受力模型，研究=0.2，=0.25，=0.3时，扰动区范围的变化，计算结果如图7所示。

1) 如图6(a)所示，泊松比变化对σ确定的扰动区范围影响较大。①当=0.2，扰动区半径的最大值在0°方向，扰动区半径为16.75 m，为隧道最大直线尺寸的8.38倍。在−75°，−30°，30°和75°方向上，扰动区半径为隧道最大直线尺寸的4~5倍。在其它方向上，扰动区范围均超过隧道最大直线尺寸的5倍。②当=0.3，在−90°和90°方向上，扰动区范围分别为11.25 m和11.5 m，分别为隧道最大直线尺寸的5.63倍和5.75倍。在其他方向上，扰动区范围均在隧道最大直线尺寸的5倍以内。

2) 如图6(b)和图6(c)所示，随着泊松比的变化，和确定的扰动区半径变化并不明显。①确定的扰动区半径的最大值在−90°与90°方向上，大致为隧道最大直线尺寸的6.1倍②确定的扰动区半径均在隧道最大直线尺寸的5倍以内。

3) 由式(7)，式(8)和式(9)可得，当泊松比为0.2，0.25和0.3时，图1模型利用弹性力学解析解确定的扰动区范围的最大值分别为隧道最大直线尺寸的8.29，6.28和6.06倍；本节基于图4数值模型所得到的最大扰动区范围分别为隧道最大直线尺寸的8.38，6.25和6.1倍。不同的处理方式，结果基本吻合，这表明了式(7)，式(8)和式(9)在确定扰动区范围上的简洁性与适用性。

因为最大扰动区半径在0°或90°方向上，因此为了简化分析过程，可以由0°和90°方向上的水平应力与铅垂应力来确定扰动区范围。

图7 泊松比变化对扰动区范围的影响

2.3.2 洞径变化对扰动区范围的影响

取隧道半径为1，1.5和2 m进行计算，计算模型同图4，计算参数同表1，结果如表2所示。

表2示出了随着隧道半径的增大，最大扰动区半径线性增大，数值解与解析解求得的最大扰动半径相近，且在泊松比确定的情况下，最大扰动区半径与隧道半径的比值是常数，这与第2节中式(7)，式(8)和式(9)所得成果是相同的。因此本节中基于隧道半径为2 m所得到的扰动区结果同样适用于其他洞径情况。

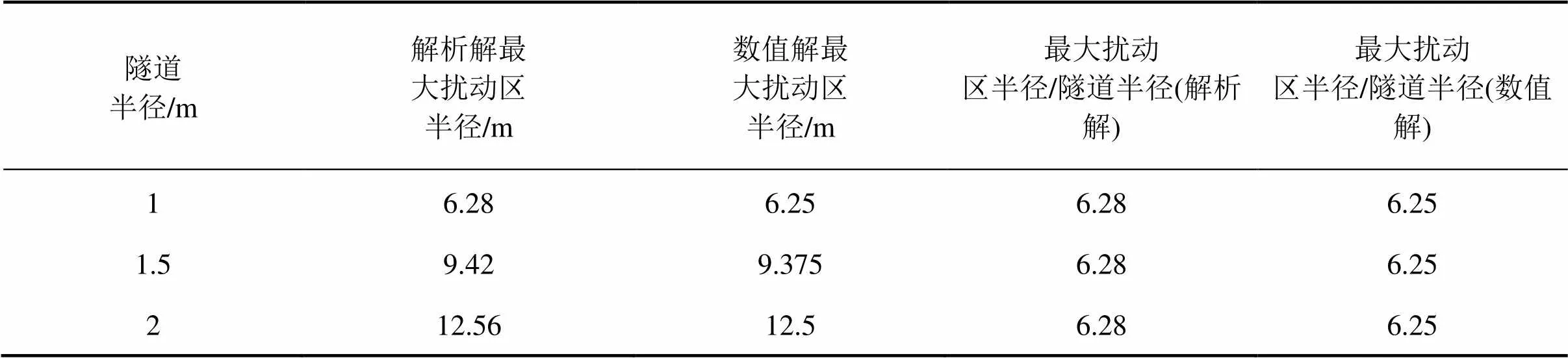
表2 最大扰动区半径与隧道半径关系

2.3.3 隧道埋深变化对最大主应力及扰动区范围的影响

取分别为300，500和900 m 3种情况进行计算，计算参数同表1，洞壁上最大主应力随夹角的变化如图8所示，可知：洞壁处最大主应力在0°方向上有最大值，随着隧道埋深增加，最大主应力不断增大。下面给出0°方向上洞壁处最大主应力随隧道埋深变化，如图9所示。

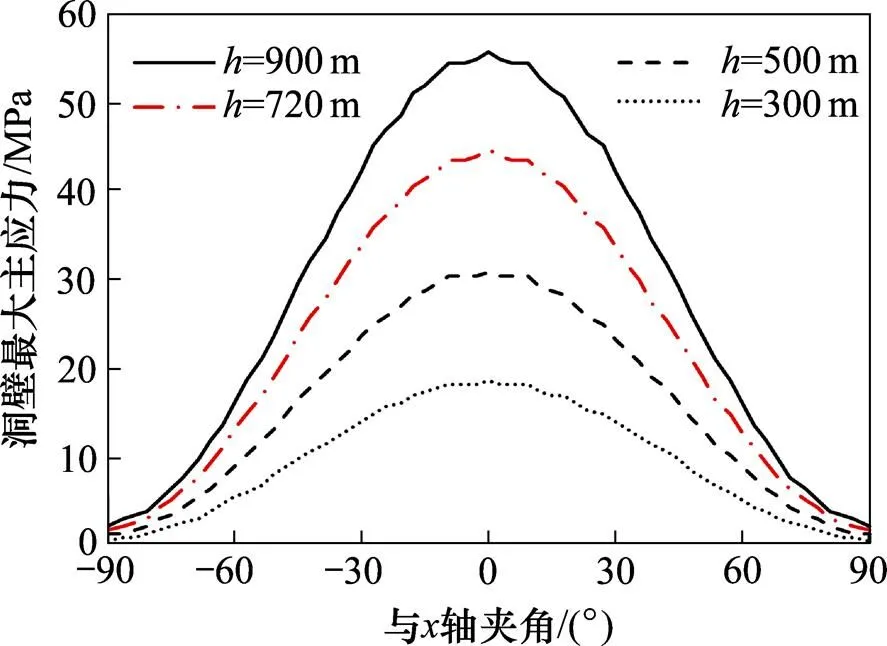
图8 洞壁最大主应力与夹角关系(μ=0.25)

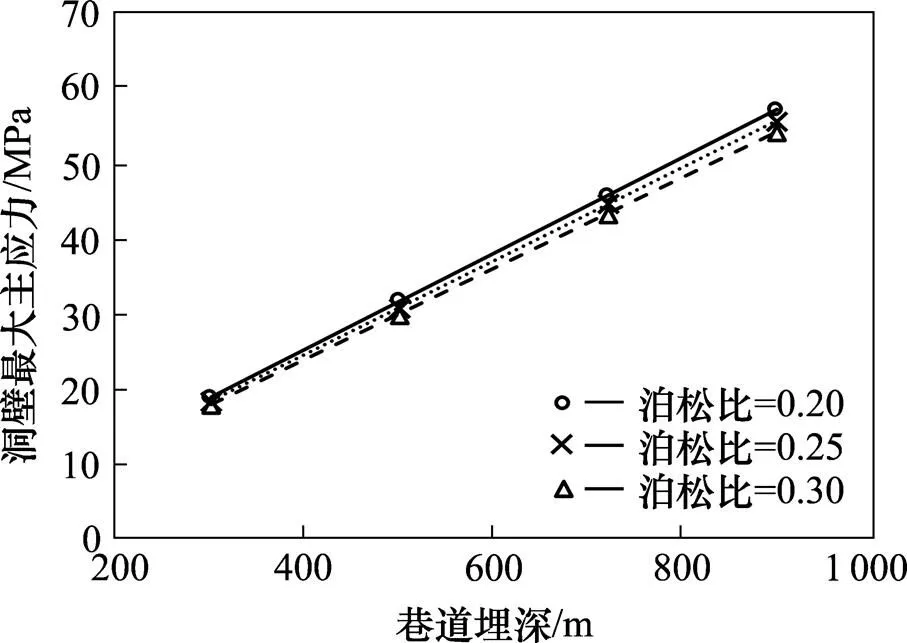
图9 0°方向洞壁最大主应力随隧道埋深变化规律

结果表明，随着隧道埋深的增加，最大主应力线性增加。尽管隧道周围应力的大小上出现变化，但是其他隧道埋深情况下应力分布规律与隧道埋深为720 m相似。经分析，前文基于隧道埋深为720 m得到的扰动区范围研究成果同样适用其他隧道埋深情况。

3 其他截面形式围岩扰动区分析

其他截面形式的隧道开挖，因难以获得围岩应力场解析解，下面以隧道中心为坐标原点建立ANSYS数值模型，分析矩形与直墙半圆拱截面形式围岩扰动区大小，它们有相同的高度与跨度，隧道尺寸如图(10)所示，地层参数同表1，数值计算模型边界尺寸及边界条件同第3节。

如图10模型，得到隧道洞壁−90°~90°方向上最大主应力与最小主应力，结果如图11所示。

图10 矩形与直墙半圆拱截面

图11 2种截面形式主应力对比

对于图10的2种截面而言，最大主应力与最小主应力峰值−45°方向附近，这与底板与侧墙相交处应力集中有关。直墙半圆拱形式的最大拉应力出现在底板中部，矩形截面形式最大拉应力值在底板与顶板中部，由于岩石抗拉强度较差，当隧道埋深较深时，底板与顶板中部岩石将以拉伸破坏的形式出现。

研究矩形与直墙半圆拱2种截面形式最大扰动区范围，研究方法同第3节，结果如图12所示。

对于图10模型而言，2种截面形式扰动区半径在−90°和90°方向上有峰值。其中，矩形截面形式最大扰动区半径在90°方向上有最大值，最大扰动区半径为15.38 m，为隧道最大直线尺寸的5.78倍；直墙半圆拱截面形式，在−90°方向上扰动区半径有最大值，扰动区半径为14.63 m，为隧道最大直线尺寸的6.27倍，最大扰动区半径均超过隧道最大直线尺寸的5倍。

图12 3种截面形式扰动区半径

由图12可知，相同高度与跨度情况下，矩形截面的最大扰动区半径最大，圆形截面的最大扰动区半径最小。因此从减小扰动区的范围角度讲，采用圆形截面要比直墙半圆拱与矩形截面更好。

4 弹塑性状态围岩扰动区分析

当隧道开挖进入深部时或地应力较大时，隧道围岩的应力场将进入弹塑性状态，若围岩弹塑性应力场的确定出现较大误差，由此得到的扰动区范围就会出现较大偏差。传统弹塑性理论采用了尚在研究的不准确的屈服准则或加载准则，这就会导致弹塑性应力场的不准确。弹塑性折线理论可以避开屈服准则或加载准则的影响，因此可以得到隧道围岩开挖扰动后弹塑性状态围岩准确应力场。

假设围岩处于小变形状态，图1与图4受力模型的边界条件将满足弹塑性折线理论的重要成果的2类边界条件[15−16]，此时，弹塑性力学问题的应力场表达式完全等同于把所讨论问题当成弹性问题求解所获得的应力场表达式。所以，即使围岩进入塑性状态，上文中的应力场解答也是准确的。因此上文中弹性状态围岩扰动分析所得到的成果将同样适用于弹塑性状态围岩扰动分析。

5 结论

1) 隧道扰动区的影响因素有隧道截面与尺寸、泊松比等。

2) 总结出了圆形隧道0°与90°方向上水平应力与铅垂应力扰动区半径与泊松比、隧道半径的多项式关系。

3) 圆形、直墙半圆拱、矩形3种截面形式的最大扰动区范围均超出了隧道截面最大直线尺寸的5倍，即一般情况下大于现时认为的3~5倍。因此数值计算模型的尺寸应根据扰动区的大小适当扩大。

4) 从减小扰动区范围的角度出发，相同高度与跨度的圆形、直墙半圆拱、矩形3种隧道截面对比，圆形截面最优，直墙半圆拱截面次之，矩形截面 最差。

[1] 高磊. 矿山岩体力学[M]. 北京: 冶金工业出版社, 1979: 83−84. GAO Lei. Mine rock mechanics[M]. Beijing: Metallurgy Industry Press, 1979: 83−84.

[2] 周辉, 渠成堃, 王竹春, 等. 深井巷道掘进围岩演化特征模拟与扰动应力场分析[J]. 岩石力学与工程学报, 2017, 3(8): 1821−1831. ZHOU Hui, QU Chengkun, WANG Zhuchun, et al. Simulating the variation of surrounding rock and analyzing the disturbed stress field during excavation of deep mine roadway[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(8): 1821−1831.

[3] 赵维生, 韩立军, 张益东. 垂直交岔点扰动主应力变化规律及围岩稳定性研究[J]. 采矿与安全工程学报, 2015, 32(1): 90−98. ZHAO Weisheng, HAN Lijun, ZHANG Yidong. Variation of disturbance principal stress and stability of surrounding rock at vertical intersection[J]. Journal of Mining and Safety Engineering, 2015, 32(1): 90−98.

[4] 唐礼忠, 陈源, 邓丽凡, 等. 扰动下含接触带巷道围岩力学响应及控制研究[J]. 铁道科学与工程学报, 2016, 13(2): 309−315. TANG Lizhong, CHEN Yuan, DENG Lifan, et al. The mechanical response features and control of surrounding rock with contact zone under dynamic disturbance[J]. Journal of Railway Science and Engineering, 2016, 13 (2): 309−315.

[5] 刘新颖, 曹平, 刘涛影, 等. 不衬砌水工隧洞围岩稳定性数值模拟分析[J]. 铁道科学与工程学报, 2012, 9(3): 45−50. LIU Xinying, CAO Ping, LIU Taoying, et al. Numerical simulation analysis of surrounding rock stability of unlined high pressure hydraulic tunnels[J]. Journal of Railway Science and Engineering, 2012, 9(3): 45−50.

[6] 董春亮, 赵光明, 李英明, 等. 深部圆形巷道开挖卸荷的围岩力学特征及破坏机理[J]. 采矿与安全工程学报, 2017, 34(3): 511−518. DONG Chunliang, ZHAO Guangming, LI Yingming, et al. Mechanical characteristics and failure mechanism of surrounding rock of deep circular roadway excavation unloading[J]. Journal of Mining and Safety Engineering, 2017, 34(3): 511−518.

[7] LONG L, KANG H, MO R. Three-dimensional plastic stress analysis of subsea tunnels: Nonlinear vs. linear-a comparison[J]. Ksce Journal of Civil Engineering, 2017, 21(1): 178−183.

[8] Zareifard M R, Fahimifar A. Effect of seepage forces on circular openings excavated in Hoek–Brown rock mass based on a generalised effective stress principle[J]. European Journal of Environmental and Civil Engineering, 2014, 18(5): 584−600.

[9] Sharan S K. Exact and approximate solutions for displacements around circular openings in elastic-brittle- plastic Hoek-Brown rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2005, 42(4): 542−549.

[10] Russo Bello F, Murphy S K. Long walling at great depth in a geologically disturbed environment. The way forward[J]. The Journal of South African Institute of Mining and Metallurgy, 2000, 100(2): 91−100.

[11] Sharan S K. Analytical solutions for stresses and displacements around a circular opening in a generalized Hoek-Brown rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(1): 78−85.

[12] 李铀, 彭意. 论圆形断面井巷围岩弹塑性应力莫尔−库伦准则解答[J]. 土工基础, 2006, 20(2): 71−72. LI You, PENG Yi. Discussion on elastic-plastic stress solution of circular section surrounding rock based on Mohr-Coulomb criterion[J]. Soil Engineering and Foundation, 2006, 20(2): 71−72.

[13] 李铀, 袁亮, 刘冠学, 等. 深部开采圆形巷道围岩破损区与支护压力的确定[J]. 岩土力学, 2014, 35(1): 226−231. LI You, YUAN Liang, LIU Guanxue, et al. Determination of failure zone and support pressure of circular roadway under deep mining[J]. Rock and Soil Mechanics, 2014, 35(1): 226−231.

[14] 李铀, 袁亮, 刘冠学, 等. 圆形巷道围岩扰动区及其临界破坏深度的确定[J]. 采矿与安全工程学报, 2016, 33(5): 795−799. LI You, YUAN Liang, LIU Guanxue, et al. Determination of disturbed region and critical failure depth of surrounding rock in circular roadway.[J]. Journal of Mining & Safety Engineering, 2016, 33(5): 795−799.

[15] 李铀. 塑性力学问题的一种求解新方法及应用[D]. 武汉: 中国科学院武汉岩土力学研究所, 2002. LI You. A new method of plasticity theory and Its application[D]. Wuhan: Wuhan Institute of Geotechnical Mechanics, Chinese Academy of Sciences, 2002.

[16] 李铀. 塑性力学引论[M]. 2版. 北京: 科学出版社, 2018. LI You. Introduction to plastic mechanics[M]. 2nd ed. Beijing: Science Press, 2018.

[17] LI Y. New research on the stress field of elastic–plastic small deformation problems[J]. Journal of Materials Processing Tech, 2003, 138(1): 508−512.

[18] 徐芝纶. 弹性力学(上册)[M]. 北京: 人民教育出版社, 1979: 267−269.XU Zhilun. Elastic mechanics (Volume 1)[M]. Beijing: People’s Education Press, 1979: 267−269.

Analysis of stress disturbed zone of tunnel and its influence factors

HE Xun, LI You

(School of Civil Engineering, Central South University, Changsha 410075, China)

The range of the disturbed zone is generally considered to be 3 to 5 times the maximum linear dimension of the tunnel cross section. The existing circular tunnel analytical solution without considering its own weight was used to determine the influence factors of the circular tunnel disturbed zone and the range of the disturbed zone within the elastic state. The polynomial relationship between the radius of the circular tunnel and disturbed zone and the tunnel radius to Poisson’s ratio was obtained. ANSYS was used to analyze the stress field and disturbed zone of the tunnel’s surrounding rocks with circular, straight wall semi-circular arch and rectangular excavation respectively. With applying the new stress field solution from the broken line theory of Elastoplastic mechanics, the results of elastic state analysis were extended to elastic-plastic state. The main results are listed as follows: The maximum disturbed zone of the three different sections (circular, rectangular and straight wall semi-circular arches) all exceeds the maximum linear dimension of the tunnel section by 5 times, which is generally greater than the current 3 to 5 times. Under the same condition of height and span, the circular cross section tunnel was found to be the best to reduce the range of the disturbed zone, followed by straight wall semi-circular arch section tunnel and rectangular section tunnel. In addition, this study provides reference for tunnel support design and the selection of numerical model calculation domain.

circular tunnel; surrounding rocks; stress disturbed zone; numerical simulation; elastoplastic analysis

U453.2

A

1672 − 7029(2019)11− 2782 − 09

10.19713/j.cnki.43−1423/u.2019.11.018

2019−02−26

国家自然科学基金资助项目(51874351)；湖南省科技计划资助项目(2014SK3226)

李铀(1961−)，男，湖南临湘人，教授，博士，从事岩石力学与工程、弹塑性力学方面的研究；E−mail：yli@csu.edu.cn

(编辑 蒋学东)