基于点线一致的既有铁路线路纵断面自动重构方法
李伟,周雨,王杰,梁家轩,彭先宝,蒲浩
基于点线一致的既有铁路线路纵断面自动重构方法
李伟1, 2,周雨1, 2,王杰3,梁家轩1, 2,彭先宝4,蒲浩1, 2
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 高速铁路建造技术国家工程实验室,湖南 长沙 410075;3. 轨道交通工程信息化国家重点实验室(中铁一院),陕西 西安 710043;4. 中铁第四勘察设计院集团有限公司,湖北 武汉 430063)
既有铁路经过长期运营,纵断面线形不可避免偏离原设计线位,必须定期重构出调整量最小且满足约束的线位,以保证列车安全运行。纵断面线形由一系列直线和竖曲线线元顺次光滑连接而成,重构关键在于准确识别每个测点归属的线元,并顾及约束进行拟合。本文提出测点归属应与重构线元完全相符的“点线一致”思想,据此构建纵断面自动重构方法。根据二阶差商初步完成测点归属识别,分别拟合对应线元,根据线元范围反向调整测点归属,迭代上述过程直至点线一致,并在迭代中处理各类约束。基于该方法研发的软件已在两千多公里既有线纵断面重构中应用,实例表明该方法可准确识别测点归属,自动生成满足约束、抬落道量显著优于既有方法的重构线形。
既有铁路;线路纵断面;点线一致;自动重构

既有铁路在长期的运营中,由于轮轨相互作用、基础变形等因素导致纵断面线形不同程度地偏离原设计线位。为保障运营安全,必须定期对既有线的轨面标高进行测量,并重构出平顺的纵断面线形,否则轨道变形累积,冲击作用恶性循环,危及行车安全,甚至引发脱轨[1]。为减少对运营的干扰,既有线纵断面重构并非简单地将变形后的纵断面轨面调整到原设计线位,而是对既有的轨面测量点进行拟合,得到一条抬落道量最小,且满足多种约束的纵断面重构线形。纵断面线形由一系列直线和竖曲线线元顺次光滑连接而成。由于直线、竖曲线的回归方程不同,因此需识别出各测点归属的线元,然后顾及各类约束分别拟合对应线元。国内外学者针对线路纵断面重构已开展大量研究,总体来说,历经3个阶段: 1)人工识别:以测点里程为横坐标,曲率、切线角、正矢等为纵坐标,生成各类线形特征图,从图中人工识别各测点归属的线元,再进行线元拟合。该类方法十分耗时,依赖设计人员的经验,识别准确度不高,重构出的线路抬落道量偏大。2)迭代识别:为克服人工识别的不足,孟凡超等[2−3]提出测点归属识别的迭代方法。该方法以人工识别分段结果为初值,以线元分界点位置稳定为收敛条件,构造迭代过程[4]。该类方法提升了测点归属识别的准确度,重构线形的抬落道量优于人工识别。但此类方法仍然需要人工参与,无法自动重构,未考虑容许抬落道量等约束。3)整体优化:近年来大量学者将纵断面重构视为最优化问题,以变坡点位置及竖曲线半径为自变量,抬落道量平方和为目标函数,建立优化模型,采用遗传算法[5]、广义简约梯度技术(GRG)等,借助数学软件[6]求解。此类方法进一步提升纵断面线形重构效果,但仍需借助前两类方法产生初值。若初值不准确,如变坡点个数识别错误,将难以产生优化的重构结果。而且此类方法同样缺少对线形约束的有效处理。除了纵断面重构,国内外学者对平面重构也开展了大量研究,先后提出方向加速法[7]、启发式算法[8]、振荡迭代[9]等一系列方法。但相比平面,纵断面直线线元间的转角较小,竖曲线半径较大、约束不同,平面线形重构方法并不完全适用于纵断面[10]。综上,国内外学者针对既有线的平纵面线形重构都开展了大量卓有成效的研究,但既有的平面重构方法难以适用于纵断面线形[11−12]。既有纵断面重构方法具有以下不足之处:1)测点归属识别精度尚待提升; 2)需人工辅助,非自动重构;3)对纵断面线形的约束处理不足。针对上述问题,本文提出基于点线一致的纵断面重构算法。该方法可以实现纵断面的全线自动精准重构,并处理纵断面重构中的各类约束。
1 “点线一致”纵断面线形重构思想
线路纵断面中直线和竖曲线线元并非独立存在,必须满足相邻线元首尾相接且相切的光顺性条件。如果依据识别的测点归属,单独拟合各直线和竖曲线线元,生成的纵断面线形无法满足光顺性条件(如图1)。而在考虑光顺性条件后,则可能出现识别的测点归属与最终拟合出的线元范围不一致(如图2),此时的线元拟合并非最优。既有的重构方法中往往将测点识别与线元拟合作为两个独立过程,忽略光顺连接问题。

图1 直曲连接处不平顺
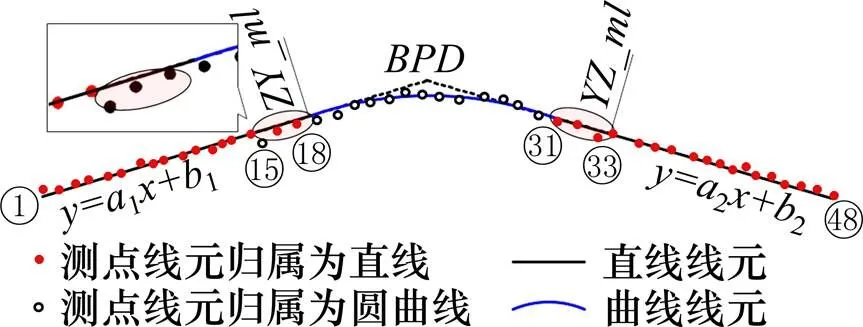
图2 测点线元归属不一致
对此,本文提出纵断面线形重构中的“点线一致”思想:对于每一组归属于直线或竖曲线的测点群,考虑光顺性进行拟合后,形成的线元刚好完全包含对应点群,此时称为“点线一致”。如果所有测点与线元均达到点线一致,则所有线元为最优拟合,测点到重构后线形调整量最小。本文不再将测点识别与线元拟合作为2个独立过程,而是基于“点线一致”思想,提出一种测点归属识别与线元拟合交错执行的循环迭代方法,其基本流程如下:
1) 基于二阶差商进行测点归属的初步识别;
2) 依据各测点归属,并顾及各类约束条件,分别拟合出直线、竖曲线线元;
3)检测拟合后的线元范围与测点归属是否达到点线一致;
4)若实现点线一致,终止迭代,得到纵断面重构线形;否则依据线元范围反向调整各测点归属,转第2步,继续迭代上述过程直到点线一致。
2 基于二阶差商的测点归属初步识别
既有铁路纵断面线形中,直线坡段与竖曲线坡段的坡度变化率有显著区别。采用既有轨面各测点的里程X和高程Y数据计算坡度变化率,可初步判断测点属性。坡度变化率为高程关于里程的二阶导数。但=()为离散函数,不可导,故采用二阶差商[13]计算二阶导数近似值:

其中:
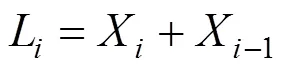


图3 既有线纵断面测点二阶差商
3 线元拟合
3.1 基于稳健最小二乘直线坡段拟合
3.1.1 稳健最小二乘拟合直线线元
测点初步分段后,首先将线元归属为直线的测点,以抬落道量平方和最小为目标,根据最小二乘原理进行直线拟合。但高程数据的粗差或异常值对拟合坡度值影响较大,解算时,应对粗差或异常值予以剔除[14],以获取稳健的直线参数最佳估值。具体解算步骤如下:
设直线坡段对应测点个数为,轨面测点数据为(x,y),直线坡段方程,坡段抬落道量平方和为:

1)()分别对,求一阶偏导为0时,可解得抬落道量平方和最小时初始值0,0:
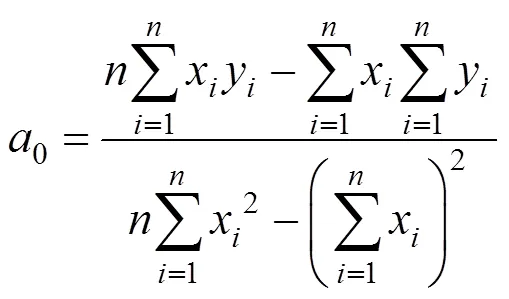

2)根据初始值0,0,计算每个测点至拟合直线的距离:
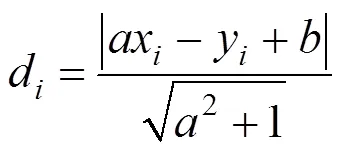
3)计算测点至直线的距离d的标准差:

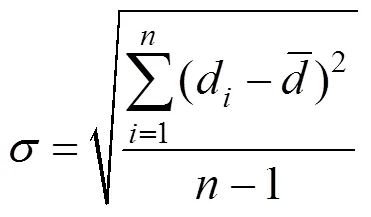
4)遍历测点,根据3原则,若d≤3,将测点保留,否则为异常点,须剔除;
5)余下测点重新进行最小二乘拟合,重复步骤1~4,直至所有测点均满足d≤3为止;
6)利用余下测点进行稳健最小二乘拟合,获取,最可靠值;
3.1.2 坡段求交
相邻2直线坡段方程联立求解变坡点坐标(X,Y):
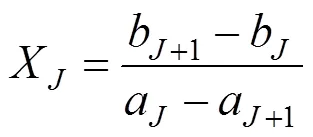

当出现下列情况时,须将相邻坡段合并,再次拟合求交:


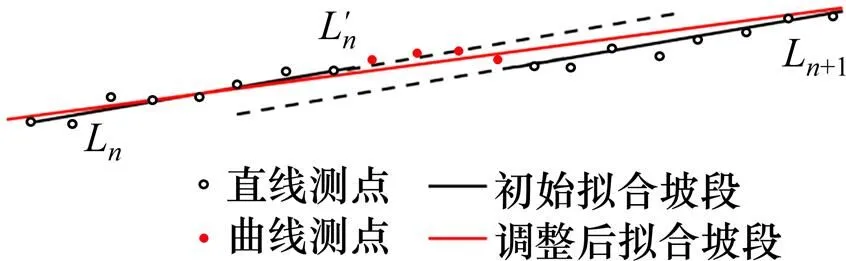
图4 相邻拟合坡段平行
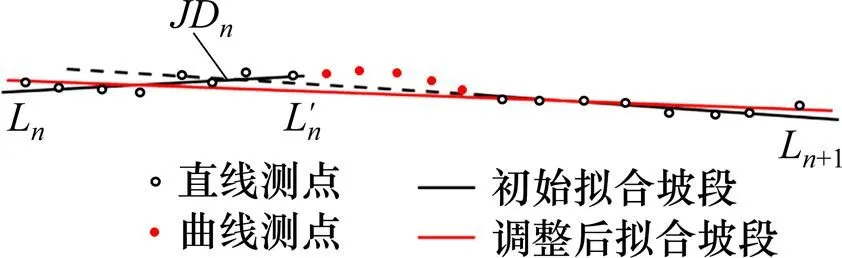
图5 变坡点未在竖曲线测点范围内
3.1.3 约束处理
纵断面直线坡段重构还存在最大坡度、容许抬落道量、最小坡长等约束。各类约束处理方法如下:
1) 最大坡度
直线坡段的方程为,其中即为坡度,需小于最大容许上行坡度imax,大于最大容许下行坡度−imax即
−imax≤≤imax(11)
2)最小坡长
①坡长接近且小于最小坡长min的坡段,向坡长较大的相邻坡段方向微调,如图6;
②坡长小于最小坡长min的坡段,与坡长较小的相邻坡段合并,如图7。
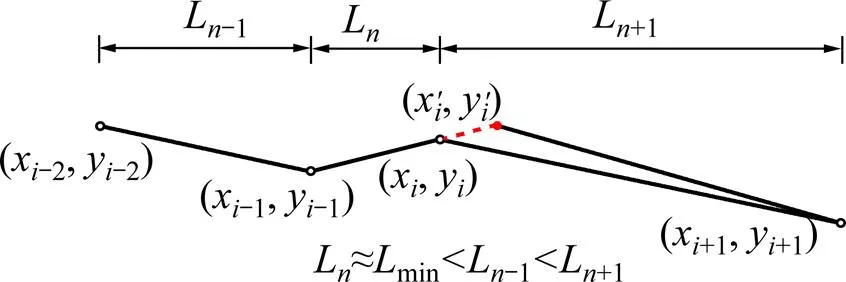
图6 变坡点微调示意图
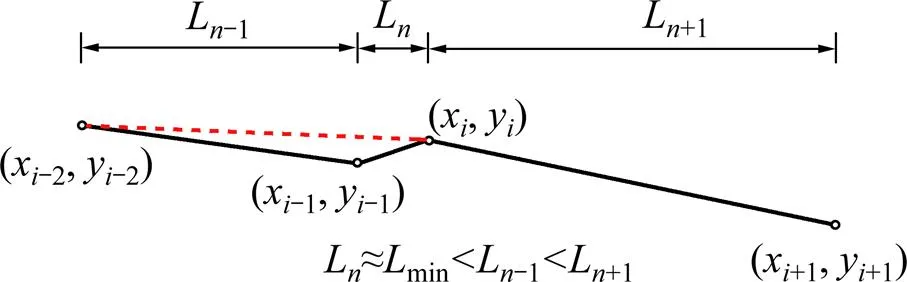
图7 相邻坡段合并示意图
3) 容许抬落道量
重构线路时,铁路纵断面存在一系列必须满足的抬落道要求,包括:
①桥梁段:不允许落道,以避免降低墩台顶面高,导致施工困难。抬道量控制在10~15cm范围,以避免道砟加厚对桥梁应力及稳定性的不利影响:
0.0≤ax+b−y≤0.15 (12)
②隧道段:一般采用落道以避免列车侵 限[15],落道量应控制在0.4m以内,以保护隧道边墙基础[15]:
−0.4≤ax+b−y≤0.0 (13)
③有支挡构造物路基段:避免因路基加宽时,填土坡脚盖过挡土墙或护坡。根据该条件反算出最大容许抬道量Tmax,则有:
ax+b−y≤Tmax(14)
④施工方法受限路段:对于不能采用抬降路基面的施工方式进行轨道调整的路段,其抬道量应小于100cm,落道量需满足最小道床厚度的要求。根据实测道床厚,可反算出容许落道量Lmax,则有:
−Lmax≤ax+b−y≤1.0 (15)
⑤运营条件约束:为减轻对运营干扰,尽量避免挖切路基或道床来降低轨面高程,因此,既有轨道尽量不进行落道。
综上,各测点须满足桥梁、隧道等特殊路段及施工方法、运营条件等多方面对抬落道量的约束,保证抬落道量在容许最大落道量−max和容许最大抬道量max之间:
−max≤ax+b−y≤max(16)
联立式(3),(11)和(16),可得出顾及最大坡度、特殊路段控制抬落道量等约束的直线坡段拟合 模型:

这是线性约束下的二元二次最优化问题,可以采用增广拉格朗日法或者序列二次规划法 求解[16]。
为提高计算效率,在实际使用过程中,可先按无约束的最小二乘拟合直线坡段。如果生成的直线满足所有约束则可直接使用,否则求解约束最优化问题。
3.2 竖曲线拟合
竖曲线部分须实现抬落道量平方和最小,同时须满足与相邻两直线线元相切的光顺性条件以及容许抬落道量、竖曲线与缓和曲线(道岔)不重叠等约束。
3.2.1 目标函数
假设竖曲线坡段测点(x,y);竖曲线半径为;前后两坡段转角为;目标函数为竖曲线范围的测点抬落道量平方和,可表示为:
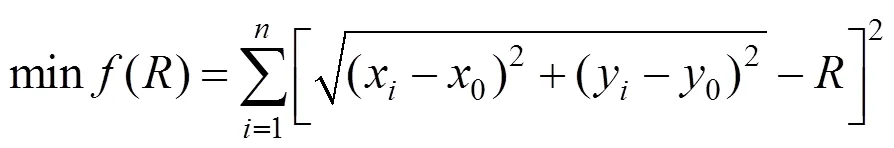
3.2.2 约束条件
1) 光顺性约束
在纵断面变坡点处,为保证行车的安全平顺,竖曲线应该与相邻直线坡段相切,如图8 所示。

图8 竖曲线与相邻直线线元光顺连接
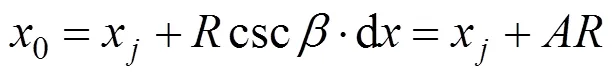
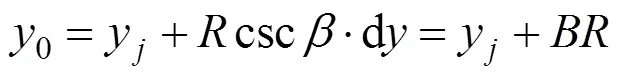
目标函数可表示为:
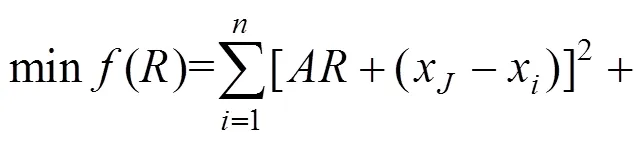
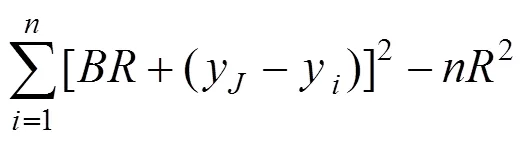
竖曲线段抬落道量平方和是关于的二次函数,当目标函数最小时,′()0,求出半径:
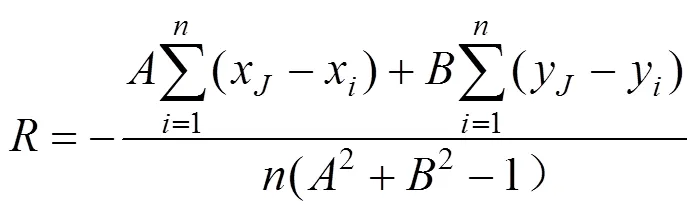
2)抬落道约束
与直线坡段一样,竖曲线段的抬落道量也应满足桥梁、隧道、支挡构造物路基、施工方法及运营条件的限制,须在最大落道量−max和最大抬道量max范围之间:−max 否则,线形须要微调至满足抬落道约束,具体方法如下: 设竖曲线圆心坐标为(0,0),满足抬落道量平方和最小的竖曲线初始方程为: 变坡点为J(XJ,YJ),容许抬落道量为∆max,相邻坡段坡度差为α,作∆PFO为直角三角形(如 图9)。 令a=FP=x−0,b=FJ=Y−y0;满足以下几何关系: 即: 满足关系式: 求解得: 其中: 抬道时maxmax,落道时maxmax。满足容许抬落道约束的取值范围为: (max)<<(max) 若初始拟合竖曲线抬落道超限,为满足拟合目标最小及容许抬落道约束,抬道时,调整取值为(max),落道时,将调整取值为(max)。 3)平纵组合约束 纵坡竖曲线部分应避免与平面缓和曲线或道岔重叠。初步确定后,计算竖曲线坡段范围(,)。若竖曲线与平面缓和曲线、道岔区重叠,须进行以下调整: ①逐步缩小,减小竖曲线范围,避免 重叠; ②若取规范半径最小值min时仍重叠,调整变坡点位置,将变坡点向重叠区域减少的方向移动,直至重叠消失; ③若变坡点移动至坡长小于规范min时仍重叠,则删除该变坡点,重新拟合求交。 为实现线形精准识别重构,完成上述测点归属初步识别和线元拟合步骤后,须检测各线元范围与识别的测点归属是否保持一致。如不一致,则通过交错迭代执行测点归属调整与线元拟合过程,最终达到点线一致。具体算法步骤如下: 步骤1:测点属性判断后,对直线测点进行稳健最小二乘直线拟合,并进行坡段求交,得到坡度及变坡点(X,Y); 步骤2:对竖曲线测点进行拟合,求出竖曲线半径; 步骤3:根据直线方程及竖曲线半径,求解特征点里程,如直圆点圆直点,如图10所示; 步骤4:分别遍历介于直线、竖曲线坡段范围内所有测点属性,如有点线属性不一致,则调整测点属性,如图11所示; 步骤5:根据调整后的测点属性,重新进行直线、竖曲线坡段拟合,如图12所示; 步骤6:重复步骤1~5,直至点线一致,得到最优纵断面线形,如图13所示。 图10 坡段拟合求交,计算特征点里程 图11 调整测点归属 图12 迭代拟合坡段,计算特征点里程 图13 实现拟合结果的点线一致 基于点线一致的迭代重构思想,笔者编制了既有铁路纵断面识别重构计算程序,通过“石门−长沙”、“宜昌东−小溪塔”等大量既有线重构算例,验证该方法较传统的坡度变化率识别等方法,在减小抬落道量平方和方面,有显著提升。 选取石门−长沙线K108+850~K128+850段为例,线路长20km,包含400个既有轨面测点,重构后变坡点共23个。传统坡度识别重构纵断面线形抬落道量平方和为36618 cm2,点线一致迭代重构的纵断面线形抬落道量距离平方和为8653 cm2。 将点线一致迭代重构与传统坡度变化率识别进行比较,点线一致迭代法重构线形的抬落道量在0~10cm范围内分布更为集中,分布范围对比如图14所示。 图14 抬落道量结果范围对比 重构完成后,依次对各坡段进行约束检测,重构线形满足纵断面各种约束,检测结果如表1所示。 表1 重构线路约束检查 1)提出了点线一致思想,基于该思想构建的铁路线路纵断面重构算法相比于既有方法,可显著减少测点到重构线路的调整量。 2)针对现有方法考虑纵断面线形约束较少的问题,处理了最小坡长、容许坡度、竖曲线与缓和曲线(道岔)不重叠、施工方法、运营条件及特殊路段(桥梁、隧道、有支挡构造物路基段)对抬落道量的约束,可直接生成满足各类约束的纵断面 线形。 3) 本方法自动化程度高,输入既有线纵断面测点里程和高程的原始数据后,可自动输出满足各类约束的纵断面优化线形。 [1] 陈峰. 提速线路精密测量、重构与优化整正研究[D].长沙: 中南大学, 2013. CHEN Feng. Research on precision measurement, reconstruction and optimal adjustment of raising speed railway[D]. Changsha: Central South University,2013. [2] 孟凡超, 刘成龙. 铁路既有线纵断面线形分段的优化算法[J]. 铁道建筑, 2014(6): 146−149. MENG Fanchao, LIU Chenglong. The optimization algorithm for linear segmentation of vertical curve type in existing railway[J]. Railway Construction, 2014(6): 146− 149. [3] 郭良浩, 刘成龙, 宋韬, 等. 铁路既有线平面和竖面线形精确分段方法研究[J]. 铁道工程学报, 2014(7): 48− 52. GUO Lianghao, LIU Chenglong, SONG Tao, et al. Research on the new method for accurate linear segmentation of plane and vertical curve type in existing railway[J]. Journal of Railway Engineering Society, 2014(7): 48−52. [4] 陈海军. 既有线有砟轨道优化线形算法研究及其软件研制[D]. 成都: 西南交通大学, 2013. CHEN Haijun. Study of algorithm on optimization design of existing railway ballast track and software development[D]. Chengdu: Southwest Jiaotong University, 2013. [5] 孙晓丽. 基于遗传算法的既有线平面及纵断面整正优化设计[D]. 长沙: 中南大学, 2010. SUN Xiaoli. Optimization design of plane and vertical section of existing railway based on genetic algorithm [D]. Changsha: Central South University, 2010. [6] Easa S M , Kikuchi S. Generalized method for estimating best-fit vertical alignments for profile data[J]. World Academy of Science, Engineering and Technology, 2009, 33: 693−701. [7] 李伟, 蒲浩, 彭先宝. 基于方向加速法的铁路既有线平面重构优化算法[J]. 铁道科学与工程学报, 2009, 6(3): 47−51. LI Wei, PU Hao, PENG Xianbao. Existing railway plane line reconstruction algorithm based on direction acceleration method[J]. Journal of Railway Science and Engineering, 2009, 6(3): 47−51. [8] Camacho-Torregrosa F J. Use of heading direction for recreating the horizontal alignment of an existing road[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(4): 282. [9] LI Wei, PU Hao. A method for automatically recreating the horizontal alignment geometry of existing railways[J]. Computer-aided Civil & Infrastructure Engineering, 2019, 34(1): 71–94. [10] Santiago Higuera de Frutos, María Castro. A method to identify and classify the vertical alignment of existing roads[J]. Computer-aided Civil & Infrastructure Engineering, 2017, 32(11): 952–963. [11] LI Wei, PU Hao, Paul Schonfeld, et al. Methodology for optimizing constrained 3-dimensional railway alignments in mountainous terrain[J].Transportation Research Part C, 2016(68): 549–565. [12] LI Wei, PU Hao, Paul Schonfeld, et al. Mountain railway alignment optimization with bidirectional distance transform and genetic algorithm[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(8) 691− 709. [13] 钟晶. 既有线改建CAD系统纵断面开发与研究[J]. 铁道勘察, 2007(6): 67−70. ZHONG Jing. Development and research on profile of CAD system transformation of existing lines[J]. Railway Investigation and Surveying, 2007(6): 67−70. [14] 官云兰, 周世健, 张立亭, 等. 稳健整最小二乘直线拟合[J]. 工程勘察, 2012, 40(2): 60−62. GUAN Yunlan, ZHOU Shijian, ZHANG Liting, et al. A robust method for fitting a line to point clouds based on TLS[J]. Geotechnical Investigation&Surveying, 2012, 40(2): 60−62. [15] 易思蓉. 铁路选线设计[M]. 湖北: 武汉大学出版社, 2014. YI SiRong. Principles of railway location and design[M]. Hubei: Wuhan University Press, 2014. [16] Nocedal J, Wright S J. Numerical optimization[M]. 2nd ed. Springer, 2006. Automatic recreating vertical alignment of existing railway based on points-alignment consistency LI Wei1, 2, ZHOU Yu1, 2, WANG Jie3, LIANG Jiaxuan1, 2, PENG Xianbao1, 2, PU Hao1, 2 (1. School of Civil Engineering, Central South University, Changsha 410075, China;2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China; 3. State key Laboratory of Rail Transit Engineering Information (CFSDI), Xi’an 710043, China;4. China Railway Siyuan Survey & Design Group Co, Ltd, Wuhan 430063, China) After a long period of operation, the vertical alignment of an existing railway inevitably deviates from the originally designed centerline. It is important for calibrating track to ensure safety and comfort. The vertical alignment consists of tangents and curves, which are connected smoothly. The key of recreation is identifying the attribution of each measured point and fitting the geometric elements considering constraints. Based on points-alignment consistency that the attributions of measured points to geometric elements should be consistent with the ranges of recreated geometric elements, a method was proposed to recreate vertical alignment automatically. After the initial identification of the points attribution using second divided difference, the corresponding geometric elements were fitted. Then the attribution of points was adjusted according to the range of geometric elements. These above processes were iterated until the points and geometric elements were consistent, meanwhile, various constraints were considered. A software system developed based on this method has been applied in the recreation of more than 2 000 km of existing railways. Applications demonstrate that this method can identify all geometric elements automatically and generate a recreated alignment while satisfying all the applicable constraints. existing railway; vertical alignment; points-alignment consistency; automatic recreating U212.34 A 1672 − 7029(2019)11− 2684 − 08 10.19713/j.cnki.43−1423/u.2019.11.006 2019−02−21 国家自然科学基金资助项目(51608543,51778640);湖南省自然科学基金资助项目(2017JJ3382) 蒲浩(1973−),男,四川南充人,教授,博士,从事铁路线站数字化设计理论与方法研究;E−mail:haopu@csu.edu.cn (编辑 涂鹏)




4 基于点线一致的震荡迭代算法




5 算例分析


6 结论

