基于随机投影的K-means算法研究
蔡 帅,朱 磊,曾维军,魏克峰,孙 静
(1.陆军工程大学 通信工程学院,江苏 南京 210001;2.战略支援部队61623部队,北京 100093;3.空军通信士官学校,辽宁 大连 116000)
0 引言
K-means聚类算法[1]最近被认为是过去50年中十大数据挖掘工具之一[2]。同时,随机投影(Random Projection,RP)或所谓的Johnson-Lindenstrausstype嵌入[3]开始流行,并在理论计算机科学[4]和数据分析[5]中得到应用。K-means聚类的目标是为数据集找到一组K个聚类中心,使得每个点到其最近聚类中心的距离的平方和最小化。虽然已知即使对于K=2,K-means聚类也是NP难问题[6],但实际上,由Lloyd提出的局部搜索启发式方法被广泛用于求解K-means聚类问题。Lloyd的迭代算法以K个任意“聚类中心”开始,并且在每次迭代中,每个点被分配到最近的聚类中心,并且每个聚类中心被重新计算为分配给它的所有点的质心,重复这最后两个步骤,直到过程稳定。
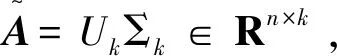
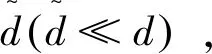
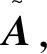
1 相关理论
1.1 近似K-means算法
K-means聚类的目的是将数据集A=[a1,a2,…,an]T∈Rn×d中的所有样本点划分到k个互不重叠的簇C={C1,C2,…,Ck}中,同一个簇中的每一个样本点与其他点之间的距离都比较近,而与其他簇中的样本点的距离都比较远。现在令μi代表第i个簇的质心,对于每一个样本点ai,它的簇标记可以表示为C(ai),K-means聚类的目标就是最小化下式:
(1)
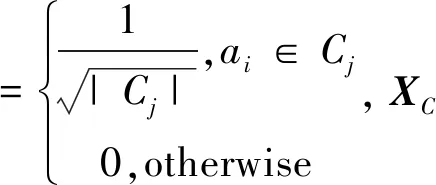
(2)

(3)
1.2 随机投影
随机投影(或者称为Johnson-Lindenstrauss嵌入)定理的一个重要结论是:对于任意矩阵A∈Rn×d,可以将其中的n个d维向量线性投影到t=Ω(k/ε2)维空间中,这种投影使用随机标准正交矩阵,并以因子1+ε保存了原始空间中任意两点之间的距离。

(1-ε)‖A(i)-A(j)‖2≤‖A(i)R-A(j)R‖2≤(1+ε)‖A(i)-A(j)‖2
(4)
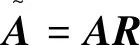
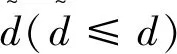
2 基于随机投影的K-means算法
2.1 基于随机投影的K-means算法
基于随机投影的K-means算法描述如下:

输入:数据集A∈Rn×d,簇个数k,误差0 <ε< 1/3输出:质心集C∈Rn×t步骤1:定义t=Ωk/ε2(),初始化t0;步骤2:生成随机矩阵R∈Rd×t,对于i=1,...,d,j=1,...,t,Rij=-1t,1t{},概率分布为1/2;步骤3:计算矩阵C=AR;步骤4:返回C∈Rn×t;步骤5:对矩阵C∈Rn×t使用K-means算法进行聚类。
2.2 K-means聚类近似算法证明
寻找XCopt是一个NP-hard问题,因此这里引出K-means问题的“γ-近似”定义:对于任何数据矩阵A的K-means问题,如果矩阵Xγ满足
(5)
那么就称矩阵Xγ是该问题的“γ-近似”,其中γ≥1。
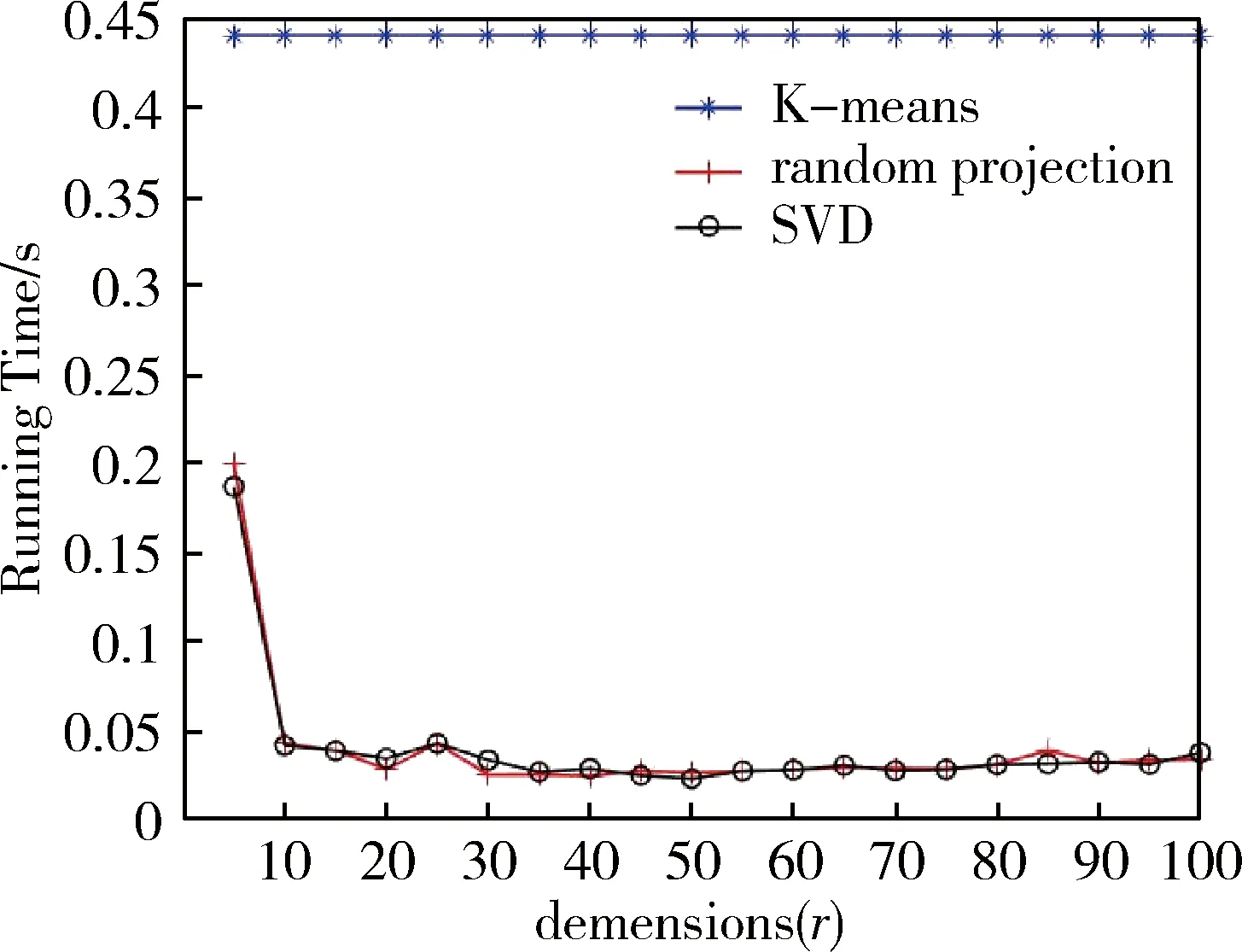
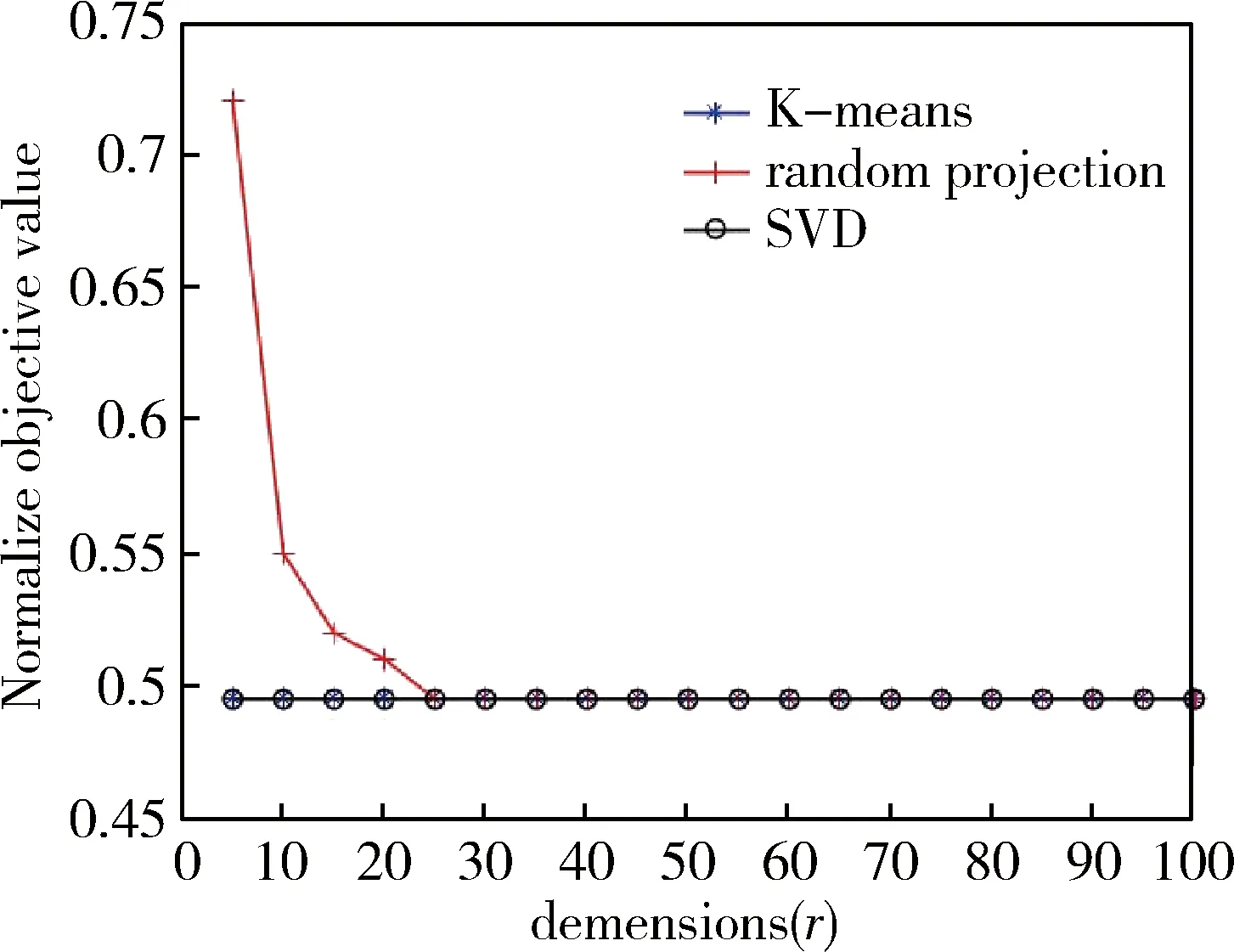
定理:令n×d矩阵A和正整数k (6) 定理简要证明: A=Ak+Aρ-k 令: 证毕。 在MATLAB中实现了所提出的算法,并将它们与其他一些显著的降维技术(如SVD)进行了比较。SVD是用于聚类的流行特征提取方法。本文在具有双核2.8 GHz处理器和8 GB RAM的机器上进行了所有实验。 在真实数据集和合成数据集上进行了实验。对于合成数据集,在n= 2 000维度中生成m= 1 000个点的数据集。从边长2 000的n维超立方体中随机均匀地选择k= 5个点作为中心点,然后,以每个中心点为中心,以方差为1的高斯分布生成其他点。对于5个中心点,生成了200个点(此处没有在数据集中包含该中心点)。因此,获得了许多分离良好的高斯,其真实中心提供了对最佳聚类的良好近似。将此数据集称为Synth。 对于面部图像集合,下载了与ORL数据库相对应的图像。此系列包含400个面部图像,尺寸为64×64,对应40个不同的人。这些图像形成40个组,每个组包含同一个人的10个不同图像。在对每个二维图像进行矢量化并将其作为行向量放入适当的矩阵之后,可以构建一个400×4 096的逐像素矩阵A。在该矩阵中,对象是ORL集合的面部图像,而特征是图像的像素值。为了在矩阵A上应用Lloyd的启发式,使用MATLAB的函数K-means,其中参数确定最大重复次数设置为30。 图1主要描述了在数据集Synth中,标准K-means算法、随机投影、SVD降准方法的运行时间与不同投影维数的关系曲线。 图1 算法运行时间比较曲线 图2主要描述了在数据集Synth中,标准K-means算法、随机投影、SVD降准方法的聚类目标函数与不同投影维数的关系曲线。 图2 目标函数比较曲线 图3 聚类精度比较曲线 图3主要描述了在数据集Synth中,标准K-means算法、随机投影、SVD降准方法的聚类精度与不同投影维数的关系曲线。 在综合数据集中可以观察到,与标准K-means算法相比,K-means算法的降维方法(RP和SVD)明显更有效。更重要的是,图3的准确度曲线表明,在这种情况下,维数降低方法也是准确的,即使相对(相对于k)小的r值。在这种情况下,数据集的聚类结果之间是完全分开的。因此,这些观察结果表明,当应用于分离良好的数据点时,K均值聚类的维数降低是有效的。实验表明,使用较小的r值运行本文算法,例如r=20或r=30,实现了高斯混合的几乎最佳分离,并且在几个真实的聚类问题中表现良好。虽然对该算法进行更全面的实验评估会提供更多信息,但初步实验结果对于该算法在实践中的表现而言是相当令人鼓舞的。 表1描述了在不同维度t下,K-means、RP和SVD在面部图像数据集的聚类精度。 对于面部图像数据集,首先通过运行2.1节算法来执行实验,其中所有内容都是固定的,t表示投影数据的维度。然后,对于t的4个代表值,将算法与SVD降维方法以及在原始高维数据上运行Lloyd启发式的方法进行比较,通过分析可以看出,在t=60时,对真实数据集的聚类效果与K-means算法聚类基本一样。 表1 算法精度比较(实际数据集) 本文研究了K-means聚类的降维问题。尽管专注于所提算法的理论基础,但在实践中测试了所提出的方法并得出结论,实验结果非常令人满意。使用所提出的方法降低了K-means算法的维数,降维后的聚类结果几乎与运行K-means算法一样准确。总而言之,本文描述了K-means聚类的一个可证明有效的特征提取算法。未来研究的一个方向是为K-means设计可证明有效的(1 +ε)误差降维方法。2.3 算法分析
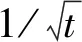
3 实验与分析
3.1 实验数据
3.2 评估方法
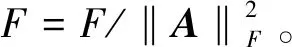
3.3 实验结果分析


4 结论

