清洁因数变化对真空严密性影响的修正计算
旷仲和
(华能国际电力股份有限公司广东分公司海门电厂,汕头 515000)
汽轮机凝汽器冷却水管的清洁因数受各种因素的影响,在运行中是变化的。众所周知,清洁因数的变化,会引起汽轮机背压的变化。而对于汽轮机真空严密性会引起什么变化,如果有变化,又如何定量计算的问题,到目前为止,文献[1-2]以及学术界未见有深入的分析研究。由此可见,有必要建立清洁因数变化对汽轮机真空严密性影响的定量解析算法,以利于对此进行比较深入的分析研究。
本文根据相关理论与高等数学计算方法,推导出清洁因数变化对汽轮机真空严密性影响的解析算法,以及清洁因数偏离规定值时修正真空严密性试验值的方法,旨在为避免清洁因数偏离设计值时对真空严密性试验值的误判断提供分析依据。
1 理论依据
1.1 清洁因数与相关参数的关系
根据文献[1]以及文献[2],清洁因数可以由下式确定:
βc=K/(Ko×βt×βm)
(1)
式中:βc为凝汽器冷却水管清洁因数;K为冷却水管总的传热系数;Ko为冷却水基本传热系数,kW/(m2·K);βt为冷却水入口温度修正因数;βm为冷却水管材质与壁厚修正因数。
参考文献[3],式(1)中的K按下式确定:
K=Qk/(A×Δtm)
(2)
结合式(1)和式(2),整理得到:
βc=Qk/(A×Δtm×Ko×βt×βm)
(3)
式中:Qk为凝汽器吸收的热量,J/s;A为凝汽器冷却水管外表面积,m2;Δtm为对数平均温差,K。
式(3)中的Qk按下式确定:
Qk=Gw×cp×(tw2-tw1)
(4)
式中:Gw为凝汽器冷却水流量,kg/s;cp为冷却水定压比热容,kJ/(kg·K);tw1为冷却水进口温度,℃;tw2为冷却水出口温度,℃。
根据汽轮机原理,Qk还要符合下式:
Qk=Dk×Δh
(5)
式中:Dk为汽轮机当量排汽流量,kg/s;Δh为当量排汽热焓与当量凝结水热焓的焓差,kJ/kg;Δh=hk-hc,hk为当量排汽热焓,kJ/kg,当工况变化时,假设汽轮机经历了绝热膨胀过程,则其根据已知的背压与当量排汽熵确定;hc为当量凝结水焓,hc=4.187(tk-0.5),0.5为设计凝结水过冷却度,kJ/kg。
式(2)中的Δtm按下式确定:
Δtm= (tw2-tw1)/ln [ (tk-tw1)/(tk-tw2)](6)
式中:tk为汽轮机排汽温度,℃。

用增量来代替上式,得到:
ΔK=Ko×βt×βm×Δβc
(7)
式(7)除以式(1),得到:
(8)
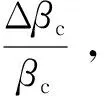
1.2 清洁因数变工况计算方法
在清洁因数变化的工况下,式(3)的A、Ko、βt、βm不变化,为常数。对式(3)求全微分,并用增量代替,得到:
Δβc= (A×Δtm×Ko×βt×βm)-1×ΔQk-
Qk×(A×Ko×βt×βm)-1×
Δ(Δtm)-2
(9)
式(9)除以式(3),得到:
(10)
由于涉及到大量参数,并且这些参数都要满足式(1)至式(10)的要求,因此,式(10)的求解计算过程与方法非常复杂。一般方法是进行试算:在选定一个βc后,假设一个背压值pk,查水和水蒸气表,得到相应的tk,然后根据其他给定的参数,分别代入式(1)至式(10),如果其结果使各式都成立,则说明其假设的背压值正确,然后建立其与设定的βc值的对应关系。否则需要反复进行上述的过程试算,直到其结果使各式都满足为止。
1.3 真空下降速度与清洁因数的关系
根据文献[1]可知:
(11)

将式(1)至式(3)代入式(11),并整理得:
(12)
对式(12)求全偏微分,并用增量代替,然后除以式(12),得到:
(13)
这样就可以把清洁因数的变工况计算简化为求各个参数增量的计算。

(14)
式(13)至式(14)表明了清洁因数变化率与真空严密性变化率的函数关系。
1.4 计算清洁因数对真空严密性影响的方法
式(14)中的分母,取两个状态点之间的中间值。
1.5 建立修正因数计算式
参考文献[2],假设两个工况下的真空严密性增量(或差值)为:

(15)
将上式变换为:
(16)


(17)
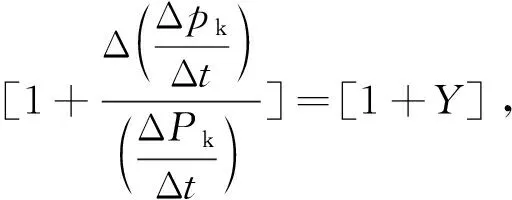
2 示例
2.1 原始数据资料(含经过整理的数据)
以某电厂超临界一次中间再热凝汽式汽轮机为例,在热耗保证工况(THA)下相关机组数据见表1。凝汽器管材为TA1。

表1 某电厂机组原始数据(含经过整理的数据)
2.2 计算内容
在上述设定工况下,在清洁因数为0.924、0.85、0.788、0.737工况下需要计算的数据以及拟合相关方程式如下:
1)清洁因数与真空下降速度以及背压之间的关系数据;
2)根据清洁因数与真空下降速度之间的关系数据,进行修正因数的计算;
3)根据上述计算得到的数据,采用文献[4]的数学二乘法,拟合清洁因数与真空下降速度之间的关系方程式,并拟合真空下降速度与修正因数之间的关系方程式。
2.3 清洁因数变化对真空下降速度的影响及其修正计算结果
有关参数及其最终计算数据、清洁因数与真空下降速度和背压之间的关系数据,以及修正因数的计算,都列于表2中(试算过程数据从略)。

表2 某厂600 MW汽轮发电机组清洁因数变化对真空下降速度影响计算
根据真空下降速度与清洁因数之间的关系数据,拟合其方程式为:

(18)
根据真空下降速度与修正因数之间的关系数据,拟合其方程式为:
1+Y=-0.482 8+2.295 5βc-
(19)
2.4 计算结果分析
本文的计算结果表明:试算的结果都能满足相关方程式;清洁因数与真空下降速度之间的关系数据能够形成光滑曲线,并能够拟合为如式(18)至式(19)这样误差极小的方程,说明该解析计算法具有足够的准确性。
根据表2计算结果分析可得:当清洁因数由设计值0.85减少至0.788时,真空严密性的修正因数由1变化到0.923 66,真空下降速度由0.27 kPa/min下降到0.249 4 kPa/min,相对变化率为7.6%。由此可见,清洁因数的变化对真空严密性具有较大的影响。这说明在清洁因数偏离设计值的情况下,对真空严密性进行修正十分必要。如果不进行修正,则会发生对规定参数下真空严密性的误判断。
清洁因数的降低会引起真空下降(也即背压升高),而背压升高会反过来使真空下降速度减小,真空严密性变好。反之亦然。其物理定性解释是:清洁因数降低引起传热系数下降,导致汽轮机背压升高,背压与大气压力之间的压差减小,由
于漏气量与压差成正比,这就使得大气漏入真空系统的漏气量相应减少,引起真空下降速度减小,使得真空严密性变好。但这种真空严密性变好,并不是在规定或设计参数条件下由于泄漏点的减少而引起,而是由于清洁因数降低,使汽轮机背压与大气之间的压差减少,而使漏气量相应减少所造成的。因此需要作此修正。
3 结 论
本文参考相关文献的基础理论以及类似的计算,推导出冷却水管清洁因数变化对真空严密性影响的解析计算方法及其修正的计算方法。根据该方法可以知道清洁因数变化对真空严密性的影响程度,并可以把真空严密性修正到规定状态。这为规范汽轮机真空严密性试验,修正清洁因数变化引起的真空严密性变化,避免对真空严密性试验值的误判断提供了计算依据与判别方法。

