回眸“方程”的发展历程

吴秀兰

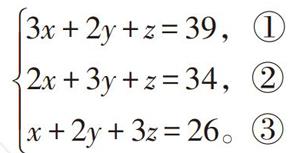
代数中引进未知数，具有划时代的意义，犹如远古时代的火、航海时代的指南针、工业革命时期的蒸汽机。方程作为人类思想的一次飞跃，是继算术思想之后的又一重要的数学思想，折射出人类的智慧。今天吴老师带着同学们一起坐上时光机，穿越到古代，看看方程的发展历程。

方程是代数史中重要的研究课题之一，它最早出现于我国的《九章算術》中。这里的“方程”其实是指一次方程组。例如：求解三元一次方程组：

[3x+2y+z=39， ①2x+3y+z=34，      ②x+2y+3z=26。③]

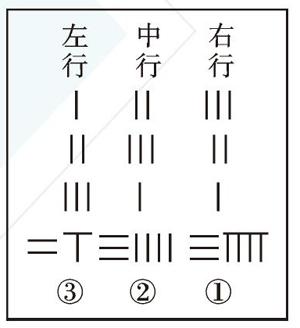
《九章算术》没有提出表示未知数的符号，而是用算筹将未知数的系数和常数项排列成一个（长）方阵（如下图），故称为 “方程”。

在世界数学史上，对方程的原始记载有着不同的形式。约3600多年前，古埃及人写在纸草书上的数学问题就涉及了含有未知数的等式。公元825年左右，数学家花拉子米为研究方程，写过一本《对消与还原》，书里详细介绍了方程的解法——还原与对消，即移项与合并同类项。宋元时期，中国数学家创立了“天元术”，用“天元”表示未知数进而建立方程，这种方法的代表作是数学家李冶写的《测圆海镜》。书中的“立天元一”相当于“设未知数”，所以在简称方程时，将未知数称为“元”，如含一个未知数的方程叫“一元方程”， 一元一次方程中的元就来自天元术。

到了17世纪，欧洲数学家韦达完成了数学的符号化。法国数学家笛卡尔最早提出用字母来表示未知数，把字母和普通数字同样看待，用运算符号和等号把字母与数字连接起来，就形成了含有未知数的等式。后来经过不断简化和改进，方程逐渐演变成现在的表达形式，例如6x+8=20，5x+2=10，x-5=2等，才有我们今天“方程”的符号化系统。

随着数学研究范围的不断扩充，方程被普遍使用，它的作用越来越大。列算式解应用题用的是小学的逆向思维;列方程解应用题运用的是正向思维，可以直接快速解决问题。由算术方法到方程方法，是数学思想的一次飞跃。接下来，我们再一起看古人如何利用一元一次方程的知识来解决实际问题。

例如，大数学家丢番图的墓碑上刻了这样一个经典问题：

过路人啊，这里安葬着丢番图，下面的数字可以告诉你他生命有多长。他生命的六分之一是愉快的童年;再过了生命的十二分之一，他的面颊上长了细细的胡须;又过了生命的七分之一，他走进婚姻的殿堂;五年后天赐贵子，他感到很幸福。可是，命运给他儿子的光辉灿烂的生命只有他生命的一半长。自从儿子死后，他的悲伤只有用研究数论去解脱。又过四年，他也结束了尘世的生涯。

我们一起来算一算丢番图的年龄。

解：设丢番图活了x岁，由题得[16x]+[112x]+[17x]+5+[12x]+4=x，解得x=84。答：丢番图活了84岁。

丢番图是第一位懂得用符号代表数来研究问题的人。同学们，我们用方程来解决这个问题，是不是相当便捷？

看了这么多，相信大家一定能体会到方程不仅形式简单，而且有非常丰富的内涵。在生活中，只要我们稍加体会，方程思想的价值便随处可见。古人在数学问题上都能不怕困难，勇登高峰，我们更应该向他们学习。让我们坐上时光机，返回现代吧。方程是从现实生活到数学的一个提炼过程，一个用数学符号提炼现实生活中的特定关系的过程。在开始学习方程时，同学们用符号表示数值关系，面临的一个困难是如何把问题的情境翻译成方程。大家要学会把日常生活中的自然语言等价地转化为数学语言，得到方程，进而解决有关问题。本次旅行结束，希望大家有所收获！

（作者单位：江苏省常州市武进区坂上初级中学）