基于最小作用量原理对经典力学规律的导出

宿非凡

(中国科学院物理研究所 北京 100080)

1 广义坐标

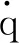
从纯力学角度来说，加速度与坐标、速度的关系式称为运动方程.对于函数q(t)来说，这个关系式是二阶微分方程，原则上，将其积分就可以求出函数q(t)继而确定系统的运动轨迹.

2 最小作用量原理与运动方程

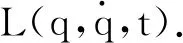
则最小作用量原理表达为

δS=0

应当说明，最小作用量原理是力学的最基本原理，很多实验和实际过程都证明了最小作用量原理的正确性.在这里将其视为基本原理，承认其正确性而不去证明.

这样一来

由变分定义可知δt=0，故有

为了统一变分变量以得到更明显的物理意义，对上式作分部积分有

由于∂q为变分虚位移，故在t1与t2时刻∂q(t1)与∂q(t2)相同为零且δq为任意值，故有

故根据最小作用原理，得到了力学中普适的运动方程

这个方程就是Lagrange方程.

从微分方程理论可知，若要完全确定力学系统的运动，必须知道描述系统在某个给定时刻状态的初始条件.而且，如果两个Lagrange量相互独立则系统的Lagrange函数可以写为

L=LA+LB

Lagrange函数的这种性质反映出：系统中每一个独立部分的运动方程不可能包含与另一部分相关的量.从运动的角度而言，这就是各个分运动之间的独立性.

至此，我们已经讨论了力学最基本系统及导出了系统的运动方程——Lagrange运动方程并对其进行了一些讨论，得到了分运动的独立性.

3 Lagrange方程与Newton定律

在研究力学体系时必须选择参考系.相对于任意参考系，空间可以是非均匀且各向异性的.但是这样一来，时间和空间的这些性质会使力学现象的描述变得极其复杂.(注：这里已经考虑了广义相对论情况)

然而，在一般的情况下我们可以找到足够“精确”的近似，即找到某种参考系，空间相对它是均匀且各向同性的，时间对它也是均匀的.这样的参考系被称之为惯性参考系.

下面从最简单的情况入手，先研究自由质点在惯性系中的运动情况，再研究有相互作用的封闭系统的运动，最后研究开放系的运动.

3.1 自由质点在惯性系中的运动

在惯性参考系中，对于自由运动的质点时间和空间的均匀性意味着这个函数不显含质点的矢径和时间t，即L只是速度的函数.由于空间各向同性，Lagrange函数也不会为速度矢量的方向，只能是速度大小的函数，也就是说L是v2n的函数,即

L=L(v2n)

不失一般性取n=1，即

L=L(v2)

Lagrange方程为

且L不依赖于空间量r,所以

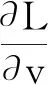
可见，在惯性参考系中任何自由运动的质点其运动的速度矢量不变.这就是Newton第一运动定律.

3.2 Galileo相对性原理与质量

实验证明：不仅在惯性参考系中满足上述讨论，在任意其他相对于这个惯性参考系匀速运动的参考系中仍然成立.这个结论称为Galileo相对性原理.

这里需指明，Galileo相对性原理只在惯性参考系中成立.这是由经典的均匀时空观所决定的，在非惯性参考系Galileo相对性原理不再成立；在时空不均匀的惯性参考系中Galileo相对性原理也不再成立.

下面讨论两个不同的惯性参考系的Lagrange函数之间的关系.基于绝对时空观Galileo变换为：在两个不同的参考系K和K′，其中K′相对K以速度v运动，同一个质点相对这两个参考系的坐标和满足关系式

在以下的所有部分中，若未特殊说明均在惯性参考系中讨论.(简称参考系)

进一步计算这两个参考系的作用量

⟹S′=S+f(q(t2),t2)-f(q(t1),t1)

可见，两个任意的参考系的作用量仅差一个附加项.而在确定边界条件之下该附加项的变分将很快消失，即有

δS′=δS

即两参考系的运动方程形式相同，符合Galileo相对性原理.由于上述讨论基于绝对时空假设，根据Galileo变换必然可以导出Galileo相对性原理.可见在绝对时空假设之下，整个讨论自洽.

进一步考虑，由前面的讨论知道自由质点在参考系中Lagrange函数只可能是v2的函数，即L=L(v2).若两个参考系相对运动速度为ε(远小于质点的速度v)，由Galileo变换可知

L′=L(v′2)=L(v2+2v·ε+ε2)

将其展开并取一阶近似有

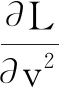
其中m为常数，这个常数就是体系的质量.

由于相互独立则系统的Lagrange函数可加性可知多系统的Lagrange函数可以表示为

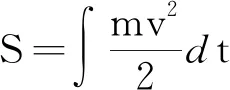
3.3 Newton第二运动定律

进一步地，在质点间有相互作用但不受外部作用的封闭体系之中，为描述质点之间的相互作用，可以在自由质点系的Lagrange函数中增加坐标的某一函数以描述相互作用.将这个函数记为-U，则

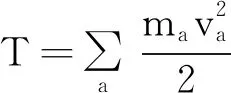
先来讨论这时的Lagrange函数，其中势能项仅依赖于系统中所有质点在同一时刻的位置，这就是说其中任意一个质点的位置改变立即会影响到所有其他质点，即相互作用可以瞬时传递.

这在经典力学中并不稀奇，它是绝对时空观假设的必然结果.如果相互作用不是瞬时传递的，即其以一个有限的速度传递，那么总可以找到两个参考系使得存在相互作用的两个物体的运动规律在同一时刻的不同参考系里不同.这明显违背了Galileo相对性原理，故相互作用必然瞬时传递.

由于Lagrange函数为

可见其在时间上是各向同性的，即用-t来替换t并不会改变其运动方程.也就是说如果在参考系中某种运动是可能的，则其逆运动也是可能的，也可以说遵循经典力学定律的所有运动都是可逆的.

在讨论清楚此时Lagrange函数的性质后，来求封闭系统的运动方程.

因为运动方程

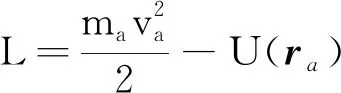
所以将其代入Lagrange方程之中，可以得到

此即Newton第二定律，是相互作用质点力学的基础，大家比较熟悉这里就不再赘言.Newton方程中的

称为作用在第a个质点上的力.其与U一样，只

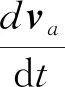
3.4 Newton第三定律

很自然地就可以将上述讨论推广到非封闭质点系.由于总可以得到一个更大的封闭系统，所以,所有上面的讨论均成立.

运动方程仍可为

设有两个相互独立的封闭系A与B，其二者的Lagrange量分别为

若选取一个更大的系统，使之包含A与B两个子系统.则A和B可视为开放系统而C为封闭系统.

这样一来，由之前的讨论可知

LC=LA+LB

且

所以有

U(ra)=-U(rb)

进一步有

可见两体系的相互作用力大小相等、方向相反、性质相同、同时产生同时消失且作用于不同的系统之上.此即Newton第三定律.

4 结束语

至此，从力学最基本的最小作用量原理导出最一般的力学体系所遵守的规律.可见，所有的经典力学的结论都可以基于最小作用量原理和均匀时空假设得到.整个推导过程有益于掌握更本质的物理内涵，明确基本物理意义且对研究更加基本的物理学有一定的启发作用.