基于自动机最简化的时序电路等价性验证方法
张留宛

摘要:为了提高时序电路等价性验证速度,提出了一种并行的验证方法。时序电路就是一种有限状态机,本文借鉴有限状态机的并行最简化方法来设计一种并行的时序电路等价性验证方法,并以实例证明了该方法的有效性和可行性。
关键词:时序电路;有限状态机;等价性
中图分类号:TP301 文献标识码:A
文章编号:1009-3044(2019)29-0235-03
1概述
随着IC产业的不断发展,出现了超大规模的集成电路,因此化简时序电路并进行等价性验证变得越来越重要。由于数字电路不同的逻辑功能特点,可以将其分为组合电路和时序电路两大类。其中组合电路具有任意时刻的输出仅取决于当前时刻的输入,和电路原有的状态无关的逻辑功能特点。而时序电路具有任意时刻的输出不仅取决于该时刻的输入,而且还取决于电路原有的状态,也就意味着,还与以前的输人有关的逻辑功能特点。
因此,化简时序电路并验证其等价性是本文所要研究的内容,因为减少其状态数即可减少时序电路中的存储元件和触发器的数量,从而达到降低成本、减少电路规模、加快电路开关速度的效果。本文提出了一种并行的时序电路等价性验证方法,该方法借鉴了有限状态机的并行最简化方法,并以实例证明了其有效性和可行性。
2传统的时序等价性算法介绍
为了验证时序电路的等价性,文献[1]提出一种改进的基于时间帧展开的时序电路等价验证算法。文献[2]将存储元素映射方法应用到时序电路等价性验证中。文献[3]将随机仿真、局部BDD、寄存器匹配和状态遍历等多种技术相结合来进行时序电路的等价性验证。文献[4]提出时序电路等价验证的触发器匹配。文献[5]提出了一种基于粒计算的状态化简算法。文献[6]提出了基于等价关系的完全确定时序逻辑电路状态化简算法,其構建状态转移系统矩阵来化简时序逻辑电路,利用等价关系将相同的列进行合并,得到最小化状态表。
3时序电路等价性定义
时序电路等同于自动机理论中的有限状态机。有限状态机是表示有限个状态与在状态之间的转移和动作等行为的数学模型,可以用其来描述时序电路系统的输入输出。本文采用Mealy型状态机来描述时序电路。Mealy型状态机描述如下:路上的输入符号均产生相同的输出符号。由此得出两个状态是否等价需满足的条件是:①在所有的输入条件下,两个状态所对应的输出是相同的;②在所有的输入条件下,两个状态的转移结果相同。等价状态是具有传递性的。也就是如果第1个状态和第2个状态等效,第2个状态和第3个状态等效,那么,一定有第1个状态和第3个状态等效。记作(s1,s2)(s2,s3)→(S1,S3)。
本文所提出的方法适用于已经给出开始状态的时序电路。在知道电路开始状态的情况下,可以使用开始状态和在此开始状态的可达状态空间形成的子状态转换图来表示时序电路。两时序电路是否等价的验证等同于验证两时序电路对应的状态转换图是否同构。如何判断两状态转换图是否同构,就是在一个状态转换图上随意取一顶点均能在另一状态转换图上找出与之等价的顶点,由此可以推断出两个状态转换图所表示的时序电路是等价的。
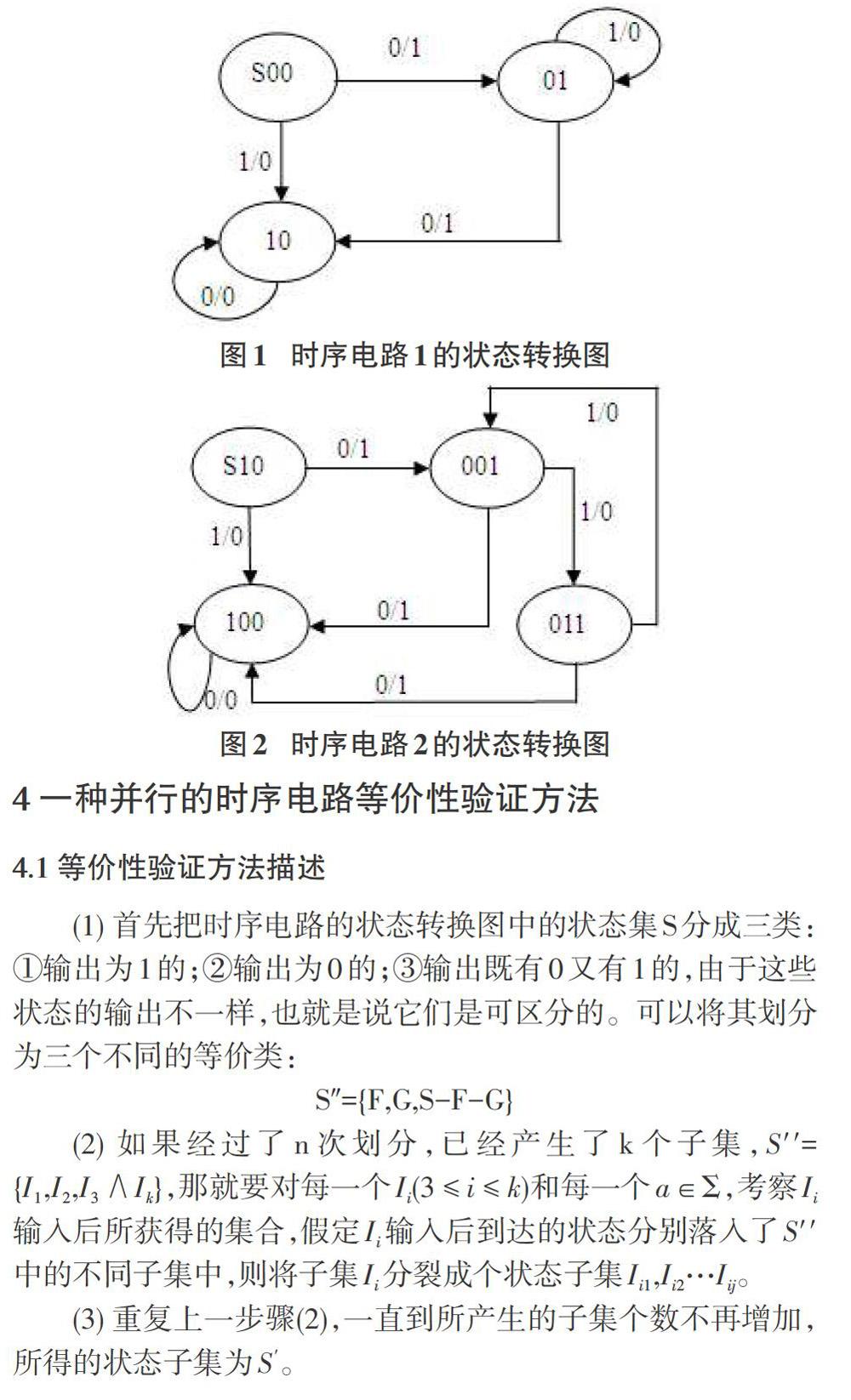
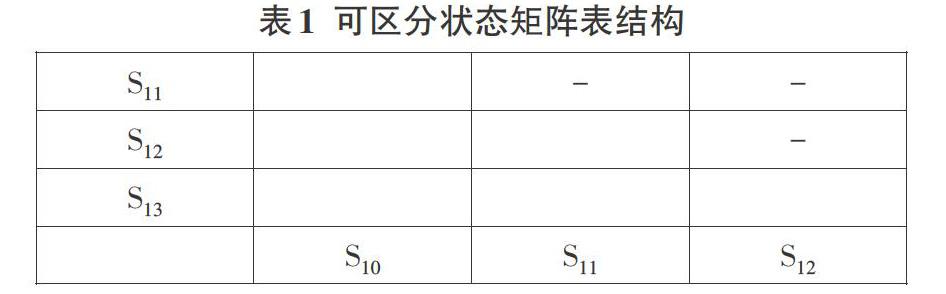
如下图1是时序电路1的状态转换图,图2是时序电路2的状态转换图,其图上的顶点代表状态,顶点与顶点之间的箭头表示状态之间的转换关系,且转换关系的条件在箭头上标注出来,其标注的格式为输入/输出。为了区别图l和图2中的顶点,本文采用不同的编号来表示图1和图2的顶点。S00和S10分别是图1和图2的开始顶点。
(4)删去状态集中的所有不可达状态,可得简化后的时序电路状态转换图。
对于一个时序电路的状态转换图如图2,构造一个可区分状态矩阵表。分别将状态001,011,100用S11,S12,s13来表示,状态表的第一列是按顺序排列的状态并删除第一个状态,相反状态表的最后一行是按顺序排列的状态并去掉最后一个状态。对于任意的状态对(q,p),判断它们是不是可以合并的,即判断他们是不是等价的。本文中(q,p)与(p,q)表示相同的状态对,即(q,p)=(p,q),因此在可区分状态矩阵表中只需要考虑对角线以下的状态对,矩阵中对角线以上的状态用“一”来进行标记,其他的表项用空来标记。图2相对应的可区分状态矩阵表结构如下表1所示:
对于上述可区分状态矩阵表进行分析,根据状态对之间的关系,首先对输出为1的状态对进行分析;其次处理输出为0的状态对;第三,输出既有0又有1的状态对可以同时进行区分。然后对已区分出的状态对相关联的状态对可以一起被区分。可以并行化处理基于此关系的可区分状态对。
对于未标记的状态对(s10,s12),(s10,S11),(s11,S12)执行do-while语句的第一次循环,每个状态对分别输入0、1,对所得到的状态对分别同时进行考察,假定有被标记过的状态对,则此状态对用“×”来标注,其所得结果如表3所示:
对剩下的没有标记的状态对(s11,s12)也执行上述操作步骤,得到的结果与表3相同,可区分状态矩阵表不再有任何变化,循环结束,由此得到最终的可区分状态矩阵表,如表3所示。
在表3中可以找出未标记的状态对(S11,S12)该状态是等价的,从而可以得到最简化的时序电路状态转换图,如图3所示:
由此可见001和011是同一状态。化简图2中的时序电路图所示的状态转换图:也就是要删除图2中的状态011,删除后的状态转换图即为图3所示。状态S00与S10即构成了待验证状态对。S00的下一个状态01与s10的下一个状态001相匹配,在输入0时即输出都为l,在输入1时即输出都为0,因此叭与001即构成了待验证状态对。状态01和001在输入1时输出都为0,在输入0时输出都为1,下一个状态分别是10和100。10和100匹配,在输入0时输出都为0,因此10和100为待验证状态对。它们的下一个状态分别为s00和S10,而s00和s10已匹配成待验证对。因此时序电路2中的状态转换图的所有状态已经验证结束,每一个待验证状态对的上一个状态对和下一个状态对都构成了待验证状态对,所有的待验证状态对均是等价状态对,因此图1和图2的状态转换图所表示的时序电路是等价的。
5结束语
文中提出一种基于STG(状态转换图)的并行验证方法,并借鉴有限自动机并行最简化原理,该方法利用并行算法将复杂的时序电路状态转换图转换成最简化的时序电路,然后再验证两状态转换图是否同构即两时序电路是否等价。克服了参考文献[7]中采用递归的方法验证两状态转换图是否同构,减少了算法的时间复杂度。

