类矩形盾构隧道衬砌结构设计模型研究

叶宇航，柳 献，刘 震，张维熙，杨志豪，朱瑶宏

（1.广州地铁设计研究院股份有限公司，广东 广州 510000；2.同济大学土木工程学院，上海 200092；3.上海市隧道工程轨道交通设计研究院，上海 200092；4.宁波大学建筑工程与环境学院，浙江 宁波 310006）

类矩形、矩形等异形盾构隧道相比于传统圆形盾构隧道具有如下优势：（1）节约地下空间，内部空间利用效率高；（2）安全埋置深度浅，穿越狭窄街区能力强；（3）相比于双圆盾构隧道具有在施工阶段容易控制背土、积浆和沉降等问题.这一新工法是缓解地下空间资源日渐紧缺问题，实现地下空间可持续发展的良策，具有广阔的应用前景.

矩形盾构法技术最早于1994年在日本得到应用，随后在日本迅速发展，其技术处于世界领先水平.迄今为止日本已建成16条规模不等的矩形或类矩形盾构隧道，其代表工程主要有：京都地铁东西线醍醐至六地藏延伸工程，采用截面尺寸为9.9 m ×6.5 m的矩形断面[1]；日本地铁东急东横线涩谷——代官山延长线工程，采用截面尺寸为10.3 m × 7.1 m的矩形断面[2]；东京都3环线道路相模纵贯川尻隧道工程中，采用截面尺寸为11.0 m × 7.08 m的矩形断面[3].但关于类矩形、矩形盾构隧道结构受力性能和设计模型方面可查阅文献较少.

目前，国内仅有上海临空11-3地块地下连接通道工程[4]和宁波轨道交通3号线出入段线工程两个类矩形盾构工程应用先例，尚未完全明确类矩形盾构隧道结构受力性能，在结构设计方面欠缺经验，结构计算模型的有效性缺乏验证.类矩形盾构隧道结构受力特点与圆形结构明显不同，类矩形结构以受弯为主，而圆形结构以受轴压为主，且本文拟研究类矩形结构有中柱结构，中柱刚度较大，其受力机制及对结构变形和内力的影响尚不明确.因此，沿用圆形盾构隧道结构设计模型必定需要对设计参数进行修正.管片整体刚度折减系数η和接缝弹簧刚度系数是结构设计模型中最主要的参数，探明上述设计参数对得到合理的类矩形盾构隧道结构设计模型和推广应用这一新型结构具有重要意义.

圆形盾构隧道结构设计参数主要依据已有工程经验、理论公式或结构试验[5-8]，但类矩形盾构隧道这一新型结构处于无据可依状态，因此十分有必要开展研究.整环足尺试验是了解结构受力性能、得到结构设计参数最有效的手段之一，国内外学者曾多次针对圆形盾构隧道进行隧道结构足尺试验研究[9-12].本文拟结合类矩形盾构隧道结构足尺试验测试结果，采用等效均质环模型和梁弹簧模型进行分析研究，得到有效的类矩形盾构隧道结构设计参数，完善类矩形盾构隧道设计理论，为类矩形盾构隧道推广应用提供支持.

1 盾构隧道衬砌结构模型

盾构隧道管片之间由于存在接缝，管片结构并非一个连续体，而是一个组合体，管片间多以螺栓连接，由于接缝受力以及接触面构造的复杂性，管片的变形和受力机理变得复杂，隧道衬砌结构模型也因此复杂多样.根据国内外学者在计算过程中对管片接缝刚度的不同力学假定，衬砌结构模型主要分为完全刚度匀质环模型、等效刚度匀质环模型、多铰环模型和梁-弹簧模型等[13].

完全刚度匀质环模型[5]在计算过程中采用与管片等刚度的环模型，不考虑接缝所引起的管片局部刚度降低.等效刚度匀质环模型[9]考虑到管片接缝的影响使管片整体刚度降低，引入折减系数η和弯矩提高率ξ，取管片环等效刚度为ηEI（η＜ 1），其中：E为材料的弹性模量；I为管片截面惯性模量.考虑到管片接缝存在铰的部分功能，将向相邻管片传递部分弯矩，使得错缝拼装管片间内力进行重分配，在计算过程中引入了ξ，主截面设计弯矩（1 +ξ）M，接缝设计弯矩（1 -ξ）M，其中，M为等效刚度均质环模型错缝位置管片截面弯矩.一般情况η、ξ的值根据试验结果和经验来确定，根据圆形盾构隧道试验结果：0.6 ＜η＜ 0.8、0.3 ＜ξ＜ 0.5，但过于笼统，参数η、ζ取值很难评判，计算结果随意性较大[14].

多铰环模型将管片接缝视为具有一定抗弯刚度的弹性铰，其承担的弯矩与其刚度成正比，抗弯刚度的大小直接影响着管片内力.需要注意的是，多铰圆环法只能在围岩坚硬强度较高的情况下使用，对于一般工程条件下，要避免使用这一计算方法[15].

梁-弹簧模型[16]将管片模拟成曲线梁或直线梁，接缝用旋转弹簧和剪切弹簧替代，弹簧的剪切和转动效应分别用径向剪切刚度K1、切向剪切刚度K2和转动刚度K3来描述，这些参数主要通过接缝试验或数值计算获得.梁-弹簧法可以对任意一种管片环组装方式和接缝位置下的衬砌环、接缝螺栓变形和内力进行计算.

上述衬砌结构设计模型主要针对圆形盾构隧道，各有优缺点，但在类矩形盾构隧道结构中是否合理尚未得到验证.且圆形盾构隧道结构设计参数一般凭经验和工程类比确定，而类矩形盾构隧道结构设计缺乏经验，因此本文拟结合整环足尺试验结果，采用等效刚度匀质环模型和梁-弹簧模型进行分析研究，确定合理的模型设计参数，得到适用于类矩形盾构隧道的结构设计模型.

2 整环足尺试验

2.1 足尺试验概况

2.1.1 试验试件

试验研究所采用的类矩形盾构隧道衬砌结构如图1所示，图中，JF1～JF10为纵向接缝编号.其外包尺寸为 11 500 mm × 6 937 mm，环宽为 1.2 m.衬砌结构由 2块 T块（T1、T2）、3块 C块（C1、C2、C3）、3块 B块（B1、B2、B3）、1块 L 块、1块 F块以及中立柱（LZ）组成，管片厚450 mm，中柱厚350 mm，宽700 mm.块与块间接缝形式为预埋铸铁手孔接缝，环向连接采用6.8级M33型螺栓连接.管片所用混凝土等级为C50，主筋为HRB400钢筋.

2.1.2 加载方案

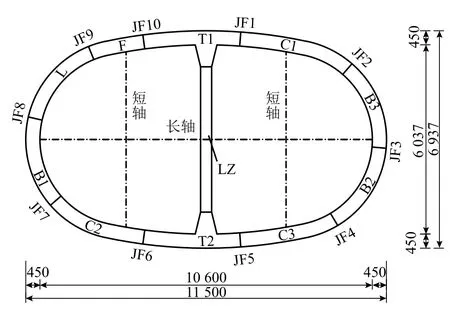
图 1 试验试件Fig.1 Schematic diagram of test specimen

为研究类矩形盾构隧道结构设计模型，针对结构在设计阶段正常运营工况进行足尺试验.试验加载装置主要由水平加载装置及滑动支座组成，如图2所示.水平加载装置包括反力框架、千斤顶（1～30）和分配梁（P1～P3），其中反力框架为试验加载提供反力作用，反力框架与地面间无约束作用，仅存在一定的摩擦力；千斤顶的油缸安装于反力框架上提供试验荷载；分配梁用于保证作用于衬砌结构的集中力沿竖向均匀分布.在试件底部与支座钢面板间放置有22盒装有钢珠的钢盒，起滑动支座的作用.

本次试验的加载装置共有30个加载点，每个加载点由2个千斤顶进行加载，采用伺服控制系统，加载时完全同步，每个加载点所能提供的最大水平荷载为2 000 kN，千斤顶的最大行程为300 mm.试验通过30个点集中荷载模拟衬砌结构在正常运营工况的实际受力，正常运营工况下衬砌结构在地层中受到垂直水土压力、水平水土压力、结构自重、地面超载和地基反力等荷载，侧压力系数为0.7.试验荷载根据11个内力控制截面内力等效将衬砌结构在正常运用工况受到的水土压力等外荷载转换为试验荷载，其中如图2中的管片 ①～⑩ 内力控制截面以弯矩控制为主，中柱内力控制截面以轴力控制为主，误差在5%以内.根据计算，试验荷载分为3组，荷载值分别为P1= 300 kN、P2= 170 kN、P3= 212 kN.

2.1.3 测试方案

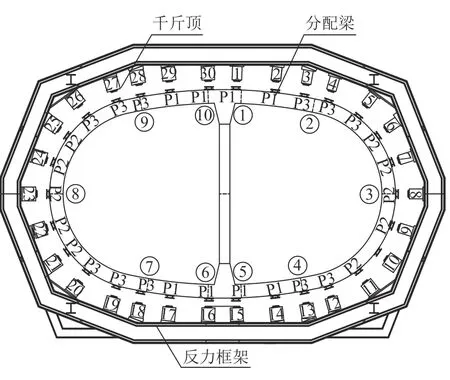
图 2 加载装置及荷载分组Fig.2 Schematic diagram of loading device and test load grouping

试验荷载作用下结构各物理量分别通过电子位移计、拉线位移计、箔式应变片进行测量.

如图3所示，整环试验共选取20个位置，布置结构整体变形测点，每个测点分别布置径向位移测点和切向位移测点，测点编号为W1～W40.选取3个位置布置结构收敛变形测点，包括1个长轴方向测点和2个短轴方向测点，每个测点在管片环宽方向布置2个拉线位移计，测点编号为SW1～SW6.

图 3 结构变形测点布置Fig.3 Layout of structure deformation measuring points

选取图2所示的内力控制截面管片主筋及端面混凝土布设电阻应变片，量测主筋及端面混凝土应变值，每个内力控制截面布置12个主筋应变片测点，12个混凝土应变片测点.主筋应变和混凝土应变测点布置如图4所示，外弧面主筋测点编号为W1～W12，内外弧面主筋测点编号为N1～N12；混凝土应变测点编号为CD1～CD12.

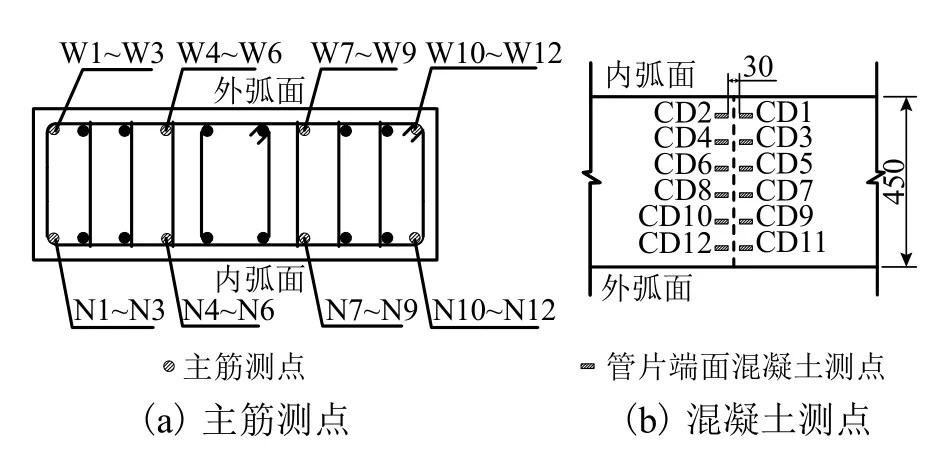
图 4 主筋及混凝土应变测点布置Fig.4 Layout of main steel bars strain and concrete strain measuring point

2.2 足尺试验结果

2.2.1 衬砌结构变形

试验通过均匀布置在衬砌结构整体变形测点及衬砌结构长短轴位置的长短轴变形测点测试得到衬砌结构整体变形图及长短轴变形值，如图5和表1所示.试验荷载作用下，衬砌结构整体变形较为对称，变形趋势表现为长轴腰部鼓出，短轴附近向内收敛.中柱左侧变形较中柱右侧变形稍大，中柱附近变形较小，最大变形位于封顶块.衬砌结构长轴变形为4.68 mm，约为长轴的0.42‰；中柱右侧短轴变形为4.74 mm，约为短轴的0.68‰；中柱左侧短轴变形为6.92 mm，约为短轴的1.00‰.

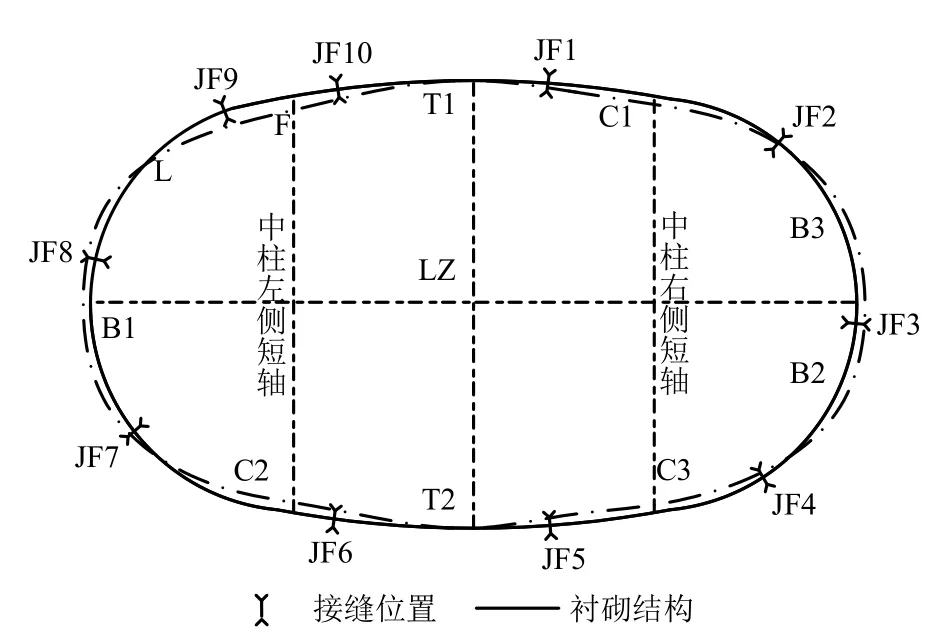
图 5 试验荷载作用下衬砌结构整体变形Fig.5 Overall deformation of ling under test load

2.2.2 衬砌结构内力

试验通过箔式应变片测得结构内力控制截面主筋应变和端面混凝土应变，在试验荷载作用下，结构仍处于弹性受力状态，假设管片截面在受力变形过程中符合平截面假定，由平截面假定可得到整个正截面应变分布，如图6所示，图中：εt为受拉区边缘混凝土拉应变；ε'c为受压区边缘混凝土压应变；εs、ε's为受拉、受压钢筋应变.

表 1 试验荷载作用下衬砌结构长短轴变形Tab.1 Long and short axis deformation of ling

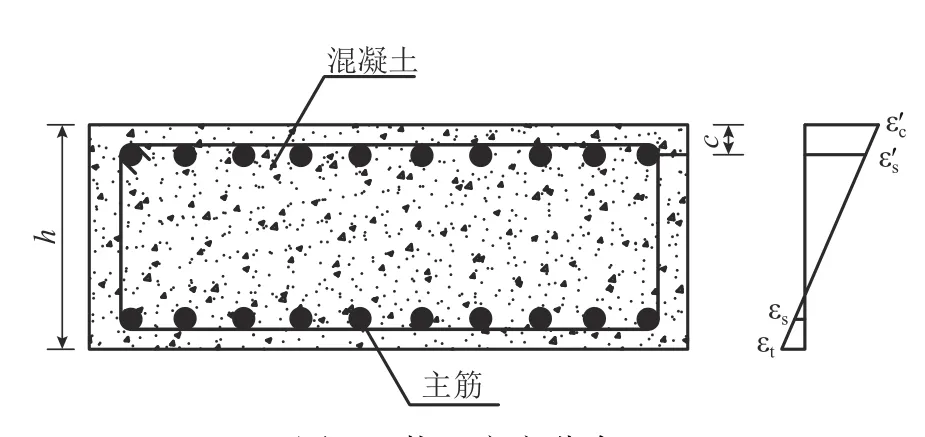
图 6 截面应变分布Fig.6 Strain distribution of segmental cross section

根据混凝土基本原理知识，可由式（1）求得结构截面内力.

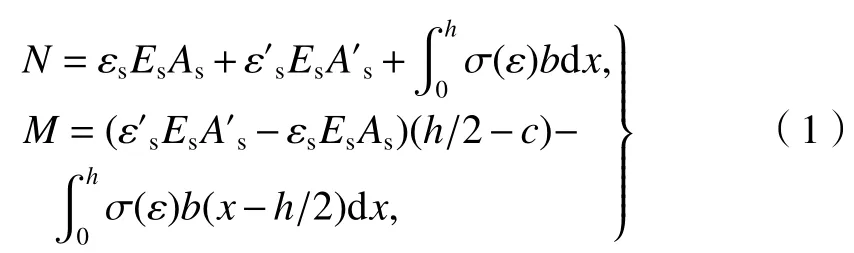
式中：Es为钢筋弹性模量；As、A's为受拉、受压钢筋面积；ε（x）为对应位置处混凝土应变；σ（ε）为对应位置处由混凝土应变决定的混凝土应力值，采用国标推荐混凝土本构关系；h、b、c分别为管片厚度、环宽以及主筋保护层厚度.

定义管片内弧面受拉、外弧面受压为正弯矩；管片内弧面受压、外弧面受力为负弯矩；中柱右侧受拉、左侧受压为正弯矩，左侧受拉、右侧受压为负弯矩；轴力受压为负，受拉为正.

试验荷载作用下，根据上述计算方法可利用试验测得的主筋应变及混凝土应变计算得到衬砌结构内力，如表2所示，由结果绘制内力，如图7和图8所示.衬砌结构截面弯矩呈对称分布，负弯矩最大值出现在中柱与管片连接处及结构腰部，最大负弯矩值为-298 kN·m；正弯矩最大值位于短轴附近，最大正弯矩值为260 kN·m.衬砌结构轴力呈对称分布，整体分布趋势表现为顶底小、腰部大，管片最大轴力位于腰部，最大轴力值为 -741 kN，中柱轴力值为 -1191 kN.

表 2 试验荷载作用下衬砌结构内力Tab.2 Internal force of ling under test load

图 7 试验荷载作用下弯矩Fig.7 Bending moment diagram under test load

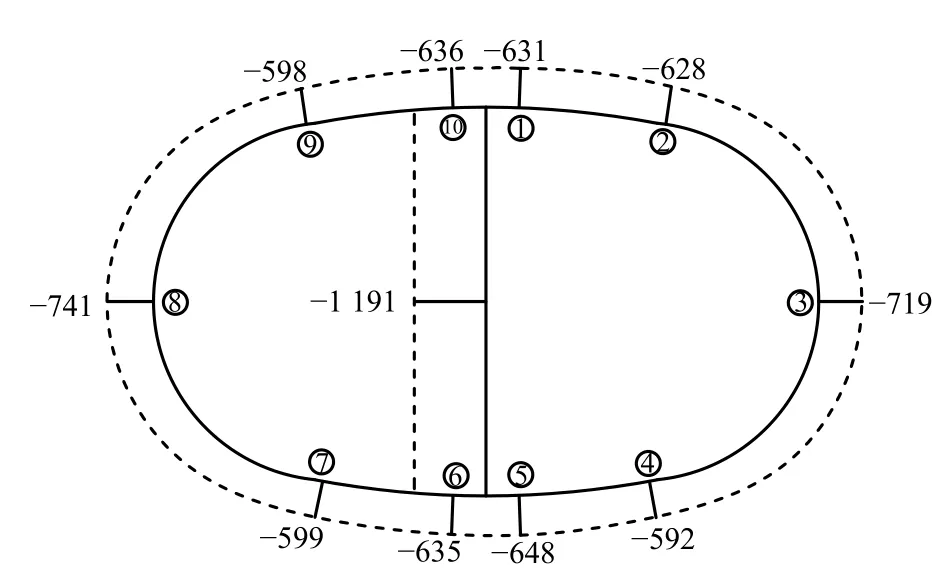
图 8 试验荷载作用下轴力Fig.8 Axial force diagram under test load

3 数值计算与试验结果对比分析

为得到适用于类矩形盾构隧道结构设计模型，本节结合整环足尺试验，采用等效刚度匀质环模型和梁-弹簧模型进行数值模拟，根据试验结果和数值模拟计算结果的对比分析，得到有效的类矩形盾构隧道结构设计参数.在数值计算中，采用衬砌结构中轴线建立模型，利用大型有限元软件ANSYS进行计算，管片及中柱单元选用beam3单元模拟，根据实际管片尺寸设置数值计算模型参数，其中：管片厚度为0.45 m，宽度为1.20 m，中柱厚度为0.35 m，宽度为0.70 m；混凝土弹性模量为34.5 GPa，结构密度为2 500 kg/m3，泊松比为0.167.在等效匀质环模型中管片设置刚度折减系数；在梁-弹簧模型中，纵向接缝弹簧采用MATRIX27单元模拟，该单元为刚度、阻尼和质量矩阵单元，可代表一种任意单元，单元的几何特性无定义，但其弹性运动学响应可用刚度、阻尼或者质量系数来指定，该单元由2个节点和系数矩阵定义，两个节点可重合，刚度、阻尼和质量矩阵中的常数可作为单元的实常数输入，其中，刚度常数单位为（力/长度）或（力·长度/弧度），在本模型中，设置MATRIX27单元长度为0，其3个方向的弹簧刚度（轴向刚度、剪切刚度、转动刚度）可在定义单元实常数时输入到刚度矩阵（12 × 12）相应位置，以模拟纵向接缝在实际受力中的转动和剪切变形，弹簧的刚度系数根据纵向接缝足尺试验数据获得.上述两个数值模型的计算荷载均与足尺试验荷载一致，分别为P1= 300 kN、P2= 170 kN、P3= 212 kN.

3.1 等效刚度匀质环模型

考虑到类矩形结构尚无完善计算理论，本文借鉴圆形盾构隧道结构设计模型，采用等效刚度匀质环模型作为类矩形盾构隧道结构模型进行计算，但由于接缝对管片刚度削减程度未知，管片的等效刚度折减系数未知，因此本次数值计算管片等效刚度折减系数分别取 0.85、0.80、0.75、0.70、0.65、0.60、0.55、0.50，立柱刚度不进行折减，对试验荷载作用下类矩形结构的变形和内力进行试算，并将内力和变形数值计算结果与试验结果进行对比分析，由计算结果可知，管片刚度折减对结构内力计算结果影响较小，但对结构变形计算结果影响较大，因此先将结构长短轴变形数值计算结果与足尺试验结果进行对比分析，如表3所示.

由表3可知，随着管片刚度折减系数减小，试验荷载作用下衬砌结构变形不断增大，当η= 0.55，0.60时，结构长轴变形数值计算结果和试验结果较为一致；当η= 0.50时，中柱左侧短轴变形数值计算结果和试验结果基本一致；当η= 0.75，0.80时，中柱右侧短轴变形数值计算结果和试验结果基本一致.总的来说，采用等效刚度匀质环模型作为预埋铸铁手孔接缝形式带立柱类矩形结构计算模型时，无法得到同时符合结构长短轴变形的管片刚度折减系数.

表 3 试验荷载作用下结构变形数值计算结果与试验结果对比Tab.3 Comparison of numerical results of structural deformation with experimental results mm

鉴于长轴变形为类矩形结构中柱左右两侧变形总和，从单跨变形来看，其变形较小，且从试验结果也可以看出，长轴变形和长轴千分比相比于短轴变形和短轴变形千分比小，因此，在设计模型中长轴变形不是结构设计的控制变形.另外由于封顶块位于中柱左侧短轴附近，封顶块管片较小，刚度较小，因此局部变形较大，所以中柱左侧短轴变形相比于中柱右侧短轴变形大.考虑到工程应用管片为AB错缝拼装隧道，管片在运营工况的实际变形应为对称变形.有研究[17-18]表明，错缝拼装相比于通缝拼装对衬砌刚度提高幅度约为10%～20%，以中柱右侧短轴变形作为设计模型的变形控制指标较为合理.因此取η= 0.75作为此次试验类矩形结构管片刚度折减系数是合理的，这和圆形盾构隧道衬砌结构管片刚度折减系数设计经验取值[19]η= 0.70相比偏大，这是由于本次试验类矩形盾构隧道管片采用了预埋铸铁手孔接缝形式，为高刚度接缝，比圆形盾构隧道管片接缝刚度大，因此接缝对管片整体刚度的削弱相比于圆形结构更小，且试验类矩形结构带有中立柱，立柱相当于刚性构件，其与T块连接处刚度远大于管片其他截面刚度，对管片变形有一定限制作用.另外，试验荷载未模拟管片在地层中受到的弹性抗力作用，考虑到地层弹性抗力对管片刚度折减系数有利[19]，因此试验结果偏保守.

由于管片刚度折减对结构内力影响较小，数值计算也表明管片刚度折减系数取不同数值结构内力计算结果基本一致，因此取η= 0.75管片刚度折减系数下内力数值计算结果与试验结果进行对比分析，如表4所示.

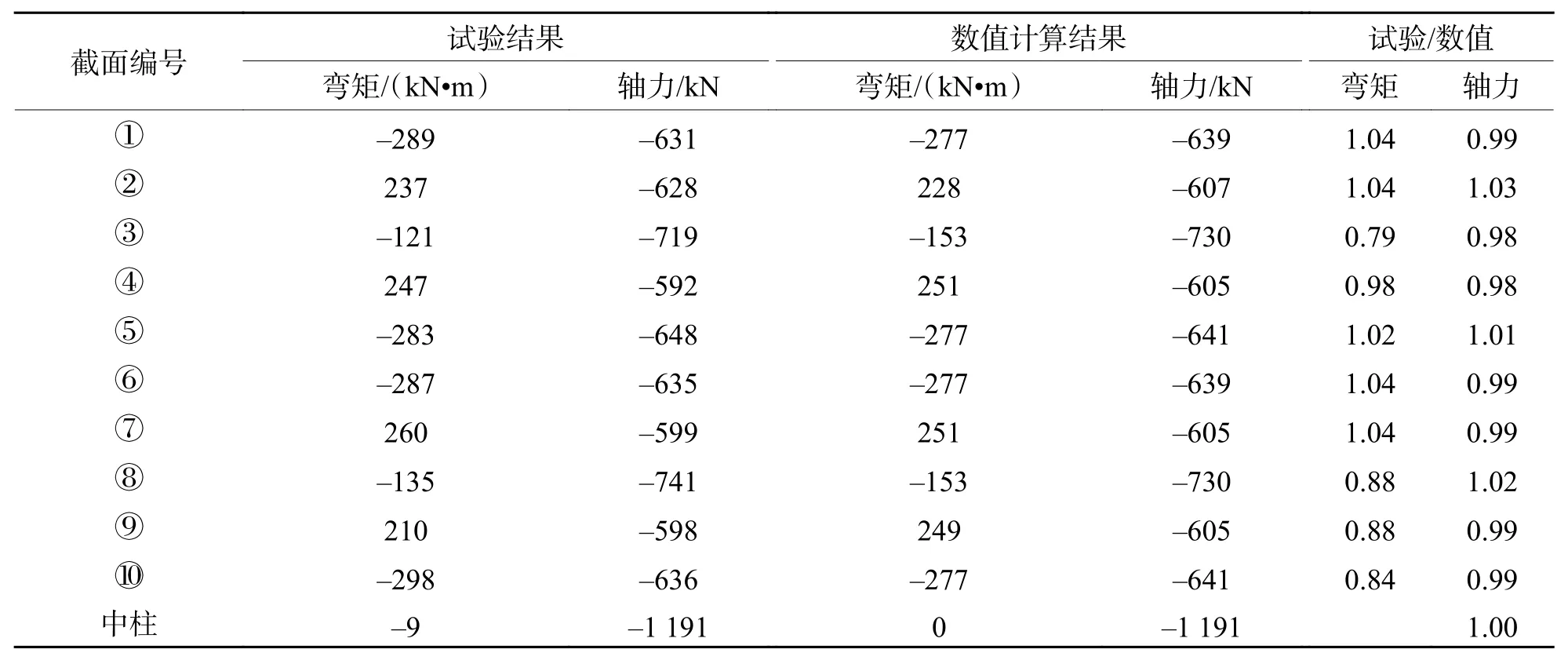
表 4 内力数值计算结果与试验结果对比分析Tab.4 Comparison of numerical results of internal force with experimental results

由表4可知，试验荷载作用下，衬砌结构轴力数值计算结果和试验结果较为一致，误差小于5%.采用等效刚度匀质环模型进行数值计算得到的结构截面弯矩和试验结果在部分内力控制截面较为接近，在部分内力控制截面相差较大，其中3号截面、8号截面、9号截面数值计算结果和试验结果相差较大，最大误差约为20%.这些截面误差较大的原因和截面位于接缝附近有关，截面弯矩相比数值计算结果偏小.在等效刚度匀质环模型中，管片截面为等刚度截面，无法考虑接缝刚度对内力的影响，接缝存在使得管片刚度有所减小，截面弯矩会发生转移，导致截面弯矩偏小，因此在接缝附近结构截面弯矩误差较大，但在其他部位计算结果相对符合，误差小于10%.

根据上述对比分析结果，采用等效刚度匀质环模型作为类矩形盾构隧道结构计算模型，无法得到同时符合长短轴变形的管片刚度折减系数；结构内力数值计算结果和试验结果较为符合，当内力控制截面靠近接缝时，截面弯矩计算结果会偏小，但仍满足设计偏于保守的要求，对于错缝拼装隧道，在内力实际计算时，需考虑错缝效应对结构内力的不利影响.综上所述，在采用高刚度接缝形式时，考虑到错缝拼装对结构变形有利，可选用管片刚度折减系数η= 0.75的等效刚度匀质环模型作为类矩形盾构隧道衬砌结构设计模型.

针对试验结构采用梁-弹簧模型进行数值模拟，接缝弹簧的接缝抗弯刚度[20]和剪切刚度取值[21]由接缝足尺试验结果得到，分别如式（2）、（3）.

式中：K4为转角刚度，MN·m/rad；e为偏心距，m.

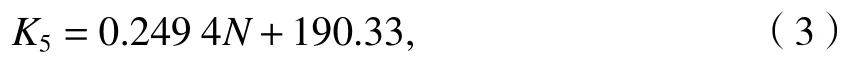
式中：K5为抗剪刚度，MN/m；N为轴力，kN.

由于接缝的刚度是与接缝内力有关，而在外部荷载条件一定时接缝的内力又受接缝刚度影响，因此，计算模型采用多次迭代的计算方法[22]对衬砌结构内力和变形进行计算，直至相邻两次计算的结构长短轴变形和内力控制截面内力误差在1%以内，停止迭代，此时的模型计算结果即为结构真实响应.

根据迭代计算结果，试验结构的梁-弹簧模型接缝抗剪刚度范围为341～368 MN/m.而接缝抗弯刚度范围根据接缝弯矩的正负性有所不同，其中JF1、JF3、JF5、JF7、JF8号接缝为负弯矩接缝，抗弯刚度范围为 114～491 MN·m/rad，2、4、6、9、10 号接缝为正弯矩接缝，抗弯刚度范围为85～177 MN·m/rad.

采用梁-弹簧模型作为类矩形盾构隧道衬砌结构计算模型时，结构长短轴变形数值计算结果和试验结果对比如表5所示.由表5可知，采用梁-弹簧模型，结构长短轴变形数值计算结果和整环足尺试验结果基本一致，误差在5%左右，说明梁-弹簧模型能较好反映类矩形盾构隧道衬砌结构实际变形情况，能考虑纵向接缝对衬砌结构变形的影响.

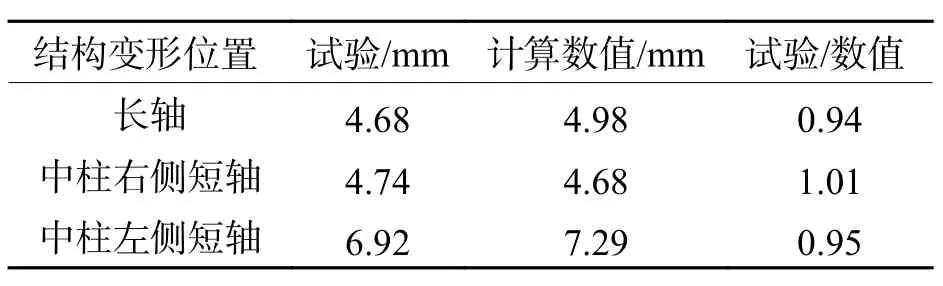
表 5 试验荷载作用下结构变形数值计算与试验结果对比Tab.5 Comparison of numerical results of structural deformation with experimental results

采用梁-弹簧模型作为衬砌结构模型时，结构内力数值计算结果和试验结果对比如表6所示.由表6可知：试验荷载作用下，衬砌结构轴力数值计算结果和试验结果基本一致，误差小于5.0%；除7号内力控制截面外，其余内力控制截面弯矩数值计算结果和试验结果基本一致，误差均在10.0%以内；7号内力控制截面弯矩误差达到18.8%，这可能与试验误差有关.对比3.1中的等效刚度匀质环模型数值计算结果，在等效刚度匀质环模型计算中，内力计算结果误差较大的3、8、9号内力控制截面，梁-弹簧模型计算结果和整环足尺试验结果基本一致，说明梁-弹簧模型能较好反映接缝对内力分布的影响.

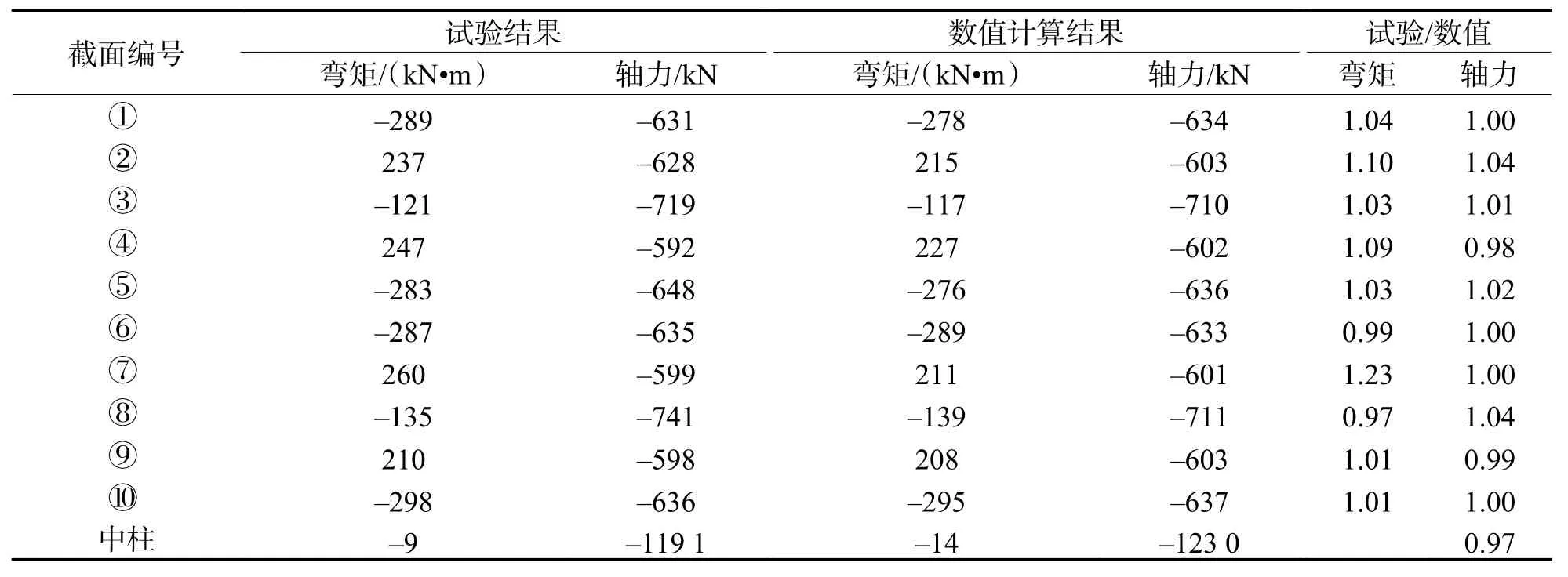
表 6 内力数值计算结果与试验结果对比分析Tab.6 Comparison of numerical results of internal force with experimental results

根据上述对比分析结果，采用梁-弹簧模型作为类矩形盾构隧道结构计算模型，结构变形和结构内力计算结果均与整环足尺试验结果较为匹配，且梁-弹簧模型能考虑纵向接缝对类矩形盾构隧道结构变形和结构内力的影响.

4 结束语

结合类矩形盾构隧道衬砌结构整环足尺试验结果，采用等效匀质环模型和梁-弹簧模型进行分析，得到类矩形盾构隧道结构等效刚度匀质环模型和梁-弹簧模型结构设计参数，得到如下结论：

（1）采用等效刚度匀质环模型作为类矩形盾构隧道结构计算模型时，无法得到同时符合结构长短轴变形的管片刚度折减系数；考虑管片为错缝拼装隧道衬砌结构整体刚度有所提高，结构变形对称，当以中柱右侧变形作为设计控制变形，纵向接缝采用高刚度接缝形式时，管片刚度折减系数可选用0.75.

（2）采用等效刚度匀质环模型作为类矩形盾构隧道结构计算模型时，结构轴力计算结果和实际较为一致，结构弯矩计算结果无法考虑接缝对内力的影响，除接缝附近截面外的其余截面弯矩计算结果和试验结果较为符合.在无法获得纵向接缝刚度参数时，可采用等效刚度匀质环模型进行内力计算，计算结果能保证设计安全性.

（3）采用梁-弹簧模型作为类矩形盾构隧道结构计算模型时，结构变形和结构内力计算结果和整环足尺试验结果较为匹配.因此，当有纵向接缝足尺试验结果或相似工程经验确定管片纵向接头刚度时，宜优先采用梁-弹簧模型进行计算.本文所述试验结构对应的管片接缝的抗剪刚度范围建议为341～368 MN/m；负弯矩接缝抗弯刚度范围建议为114～491 MN·m/rad，正弯矩接缝抗弯范围为85～177 MN·m/rad.

（4）采用梁-弹簧模型作为类矩形盾构隧道结构计算模型能考虑纵向接缝对结构变形和结构内力分布的影响，能真实反应类矩形盾构隧道结构受力特性，因此，选用梁-弹簧模型作为类矩形盾构隧道结构计算模型更为合理.

本文研究的类矩形盾构隧道结构不同接缝对结构受力性能的影响程度不同，后续工作可通过参数分析研究不同部位对结构受力性能的敏感性，并通过优化接缝构造提升结构受力性能.另外，本文未研究类矩形盾构隧道错缝模型，且类矩形盾构隧道这一新型结构的在意外工况下的整体安全性也尚不明确，仍需要进一步研究.