振子网络中内能和熵的探究

肖琴 许庆祥 杨会杰 严捷冰

摘 要： 将复杂网络视为振子网络，对小世界（WS）网络、Barabasi & Alber（BA）网络和实际的酿酒酵母蛋白质相互作用（PPI）网络的内能和熵进行了分析.分析结果表明：随着网络节点数、连边概率、热浴温度等参数的变化，不同网络的内能和熵的变化趋势差异很大，可以以这种差异来判别网络的类型.

关键词： 振子网络; 内能; 熵

中图分类号： N 941  文献标志码： A  文章编号： 1000-5137（2019）05-0472-07

Abstract： By considering the complex network as oscillator network，the internal energy and entropy were analyzed for small world network，Barabasi & Alber（BA） network，Logistic chaotic series visibility graph and the real saccharomyces cerevisiae protein-protein interaction （PPI） network.The analysis results showed that the variation trends of internal energy and entropy for different networks were changed greatly with parameters such as the number of network nodes，the probability of connecting edges and the hot-bath temperature.Furthermore，the type of the network could be discriminated by such differences.

Key words： neton network; internal energy; entropy

0 引 言

对振子网络动力学及其实际意义的研究已经成为复杂网络[1-2] 研究领域的热点.振子网络动力学在对生物系统[3]、多智能体网络[4]、耦合振子网络[5]以及振子网络的同步[6-8]等方面的研究中起到重要作用，其中的网络振子能被用来探测发生在许多复杂系统中的动力学过程，如代谢网络中代谢物在不同浓度下的振动过程.

KIM等[9-10]应用振子网络研究了不同网络上晶格振动与频谱之间的相互关系，ESTRADA等[11]在其基础上研究了网络振子的势能函数.XU等[12]和ZHOU等[13]分析了带有时滞的小世界（WS）网络的稳定性、不稳定性，以及Hop分岔和控制等.

对于一个社会网络[14]的振子，一般至少受到两个方面的影响，即其他节点的影响和环境影响.本文作者将复杂网络构建成振子网络，运用振子网络的动力学方程，分析了WS网络和Barabasi & Albert（BA）网络在振子热浴条件下的热力学性质.以振子网络的内能和熵为对象，对以上两种不同类型的网络进行了分析.最后对真实的酿酒酵母蛋白质-蛋白质相互作用网络（PPI）的内能和熵进行了分析，通过两者的变化，可判断其为BA网络.

1 模 型

如果把复杂网络中的节点视为质量均为M的小质点，将连边看成是连接2个小质点，弹性系数为K的弹簧，那么复杂网络就转换成了一个振子网络.若将该振子网络置于温度为T的热浴中，小质点会在热扰动下振动，构建出复杂网络在外部环境影响下的振动模型.当系统与环境达到热平衡时，由能级谱可以获得能量和熵等统计量，并发现非平凡的结构模式能引起物理性质的显著变化.网络结构的改变可以形成网络不同的热力学特性，反之，不同的热力学特性也反映了网络结构不同的动力学性质.为简化讨论，本研究假设系统内没有阻尼，也没有其他外力作用于该系统.

2 实验过程和结论

以WS网络和BA网络为例，分析了不同网络内部的内能和熵随着温度以及网络节点数变化而变化的规律.由于变化规律相似，对应于不同情况，本文作者随机取了一种特殊情况进行分析.对于不同的网络类型，其内能和熵的变化与网络结构密切相关.

2.1 WS网络

WS网络[15]是WATTS和STROGATZ于1998年提出的，它将规则网络和随机网络结合在一起，具有较大的平均集聚系数和较小的平均距离，引起了对复杂网络的研究热潮.WS网络的形成过程为：1）从一个总节点数为N且每个节点与最近邻2k个节点相连的环状晶格开始，为了保证网络的稀疏性，令N2klnN1;2）随机选取网络的一条边，按一定连边概率p对该边进行重新连接.在构建网络的过程中，须保证重连过程中网络没有自连边和重复的连边.

考虑当最近邻边为4时（k=2）网络的3种情况：

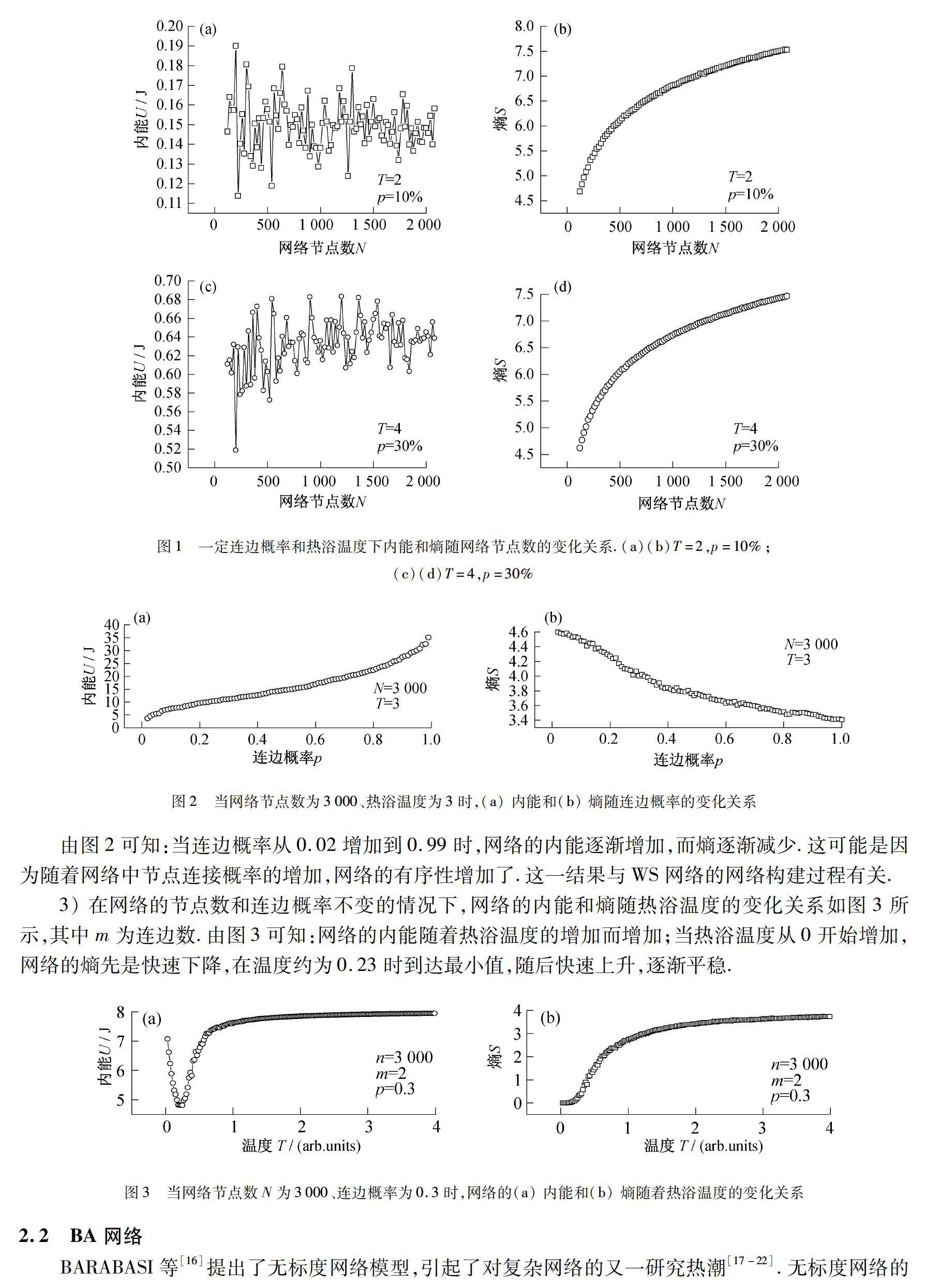
1）当连边概率分别为10%，30%，热浴温度分别为2，4（arb.units）时的内能和熵随着网络节点数（100～2080）的变化关系，如图1所示.

比较图1（a），1（c）可知：当热浴温度与连边概率一定时，内能并不随着网络节点数的增加而增加，而是趨向于某个定值，并在此定值附近震荡;而当温度与连边概率变大，该定值也会变大.比较图1（b），1（d）可知：熵随着网络节点数的增加而增加，且随着温度与连边概率的增大，网络的熵变小.

2） 当网络节点数N为3000、热浴温度为3时，网络的内能与熵随连边概率p（0.02～0.99）的变化关系如图2所示.

由图2可知：当连边概率从0.02增加到0.99时，网络的内能逐渐增加，而熵逐渐减少.这可能是因为随着网络中节点连接概率的增加，网络的有序性增加了.这一结果与WS网络的网络构建过程有关.

3） 在网络的节点数和连边概率不变的情况下，网络的内能和熵随热浴温度的变化关系如图3所示，其中m为连边数.由图3可知：网络的内能随着热浴温度的增加而增加;当热浴温度从0开始增加，网络的熵先是快速下降，在温度约为0.23时到达最小值，随后快速上升，逐渐平稳.

2.2 BA网络

BARABASI等[16]提出了无标度网络模型，引起了对复杂网络的又一研究热潮[17-22].无标度网络的形成过程为：1）当t=0时，网络共有m0个节点;2）每1步增加1个节点，与m（m≤m0）个旧节点相连;3）加入的节点与第i个节点相连的概率pi=ki∑Nj=1kj，其中，ki为节点i的度，kj为节点j的度，由于这个网络是变化的，新加入的点根据度选择连边，选择定了后面网络的连接发生了改变;4）当网络达到稳定状态后停止生长.

在BA网络中，同样考虑3种情况：

1） 当初始节点数m0为200、网络节点数N为2000、热浴温度T为1时，网络的内能和熵随连边数m的变化关系，如图4所示.由图4可知：当连边数改变时，网络的熵几乎为定值（7.6），上下浮动很小，而网络的内能随着连边数的增加而增加.

2）当m0=100，m=2，T=1时，网络的内能和熵的随网络节点数N（130～3 030）的变化关系如图5所示.由图5可知：随着网络节点数的增加，网络的内能反而减少，而熵越来越大.使用不同的初始节点数、连边数目和热浴温度，变化趋势相同.这一結果可能与BA网络的结构有关，当初始节点数、连边数目和温度不变时，网络节点数的增加使网络变得越来越稀疏，导致内能减少，而熵即无序性增加.

3）当m0=200，m=7，N=2000时，网络的内能和熵随热浴温度的变化关系如图6所示.由图6可知：网络的内能和熵基本一致，当温度低于0.23前，变化很小;当温度介于0.23与0.50之间时，快速上升，之后逐渐趋向稳定.

3 酵母蛋白质相互作用网络的内能和熵的分析

蛋白质是生物功能的最终执行者，蛋白质和蛋白质之间的相互作用是蛋白质发挥作用的重要方式[23]，因此研究蛋白质之间的相互作用是当前生物学研究的一个重点内容.目前，对于酿酒酵母（Saccharomyces Cerevisiae）这种单细胞的真核生物，已经建立了蛋白质数据库，能在全基因组水平上研究蛋白质之间的相互作用.学者们用不同的方法构建了几种不同置信水平的PPI网络.

研究者们分析了5种置信水平不同的酿酒酵母蛋白质相互作用网络.将文献[24]中的高置信度的酵母PPI网络记为“YHC”，其和前11000个相互作用的酵母PPI网络记为“Y11K”.文献[25]中的“核心”酵母PPI网络记为“YIC”，文献[26]中的酵母PPI网络记为“YU”，结合了两者的酵母PPI网络记为“YICU”.它们分别来自不同的高通量研究方法，其中YHC和Y11K主要来自于串联亲和纯化[27]和高通量质谱蛋白质鉴定[28]，而YIC，YU和YICU则来自酵母双杂交.

图7为5种实际PPI网络的内能和熵与环境温度的关系图.由图7可知：YIC和YU这2种由酵母双杂交的PPI网络的热力学性质几乎完全一样.而它们的组合——YICU的PPI网络在熵值上的区别较大.对于分别来自串联亲和纯化的YHC和高通量质谱蛋白质鉴定的Y11K的PPI网络之间的差别也较大.因此可以认为：由不同方法构建的蛋白质相互作用网络的热力学性质有着显著的差异.

另外，由图7还可知：随着热浴温度的升高，5种蛋白质相互作用网络的内能和熵都增加了，这与BA网络的变化相同.BARABASI等 [29]对酵母PPI网络的分析说明度其分布满足幂律分布，为BA网络.这一结果说明网络内能和熵随网络参数的变化特征差异有可能作为判别网络类型的表征.

4 结 论

WS网络和BA网络是现实生活中非常常见的网络，它们在网络构建方式上和网络的异质性质上有很大的不同.本文作者在3种情况下比较和分析了这两种网络的热力学性质：首先在网络节点为定值的情况下，随着连接概率或连边数的增加，WS网络的内能增加，熵值减少，而BA网络内能增加，熵值趋向于一个常数;其次在连边概率或数目为定值而网络节点增加的情况下，WS网络内能趋向一个定值，熵值递增，而BA网络内能减少，熵值增加;最后在节点数目等条件均为定值只有温度增加的情况下，WS网络的内能增加，熵值先减后增，而BA网络的内能增加，熵值增加.对实际酵母PPI网络的内能和熵值的计算也表明：网络的热力学性质能反映出网络结构上的不同，内能和熵值的变化也能反映出网络的内部的动力学特征.

参考文献：

[1] YANG Y，YANG H.Complex network-based time series analysis [J].Physics A，2008，387：1381-1386.

[2] WANG J，YANG H.Complex network-based analysis of air temperature data in china [J].Modern Physics Letter B，2009，23：1781-1789.

[3] REN J，LI B.Thermodynamic stability of small-world oscillator networks：a case study of proteins [J].Physical Review E，2009，79（5）：051922.

[4] ZHOU J，ZHANG H，XIANG L，et al.Synchronization of coupled harmonic oscillators with local instantaneous interaction [J].Automatica，2012，48（8）：1715-1721.

[22] YANG Y，GU C G，XIAO Q，et al.Evolution of scaling behaviors embedded in sentence series from a story of the stone [J].The Public Library of Science One，2017，12（2）：e0171776.

[23] FIELDS S，SONG O.A novel genetic system to detect protein-protein interactions [J].Nature，1989，340：245-256.

[24] VON M C，KRAUSE R，SNELl B.Comparative assessment of large-scale data sets of protein-protein interactions [J].Nature，2002，417（6887）：399-403.

[25] USTZ P，GIOT I，CAGNCY G et al.A comprehensive analysis of protein-protein interactions in cerevisiae [J].Nature，2000，403：623-627.

[26] ITO T，TASHIRO K，MUTA S，et al.Toward a protein-protein interaction map of the budding yeast：a comprehensive system to examine two-hybrid interactions in all possible combinations between the yeast proteins [J].Proceedings of the National Academy of Sciences，2000，97（3）：1143-1147.

[27] GAVIN A C，BOSCHE M，KRAUSE R，et al.Functional organization of the yeast proteome by systematic analysis of protein complexes [J].Nature，2002，415：141-147.

[28] HO Y，GRUHLER A，HEIBUT A，et al.Systematic identification of protein complexes in saccharomyces cerevisiae by mass spectrometry [J].Nature，2002，415：180-183.

[29] BARABASI A L，ALBERT R.Emergence of scaling in random networks [J].Science，1999，286（5439）：509-512.

（責任编辑：顾浩然）