复合地层中不同盾构掘进参数下碴土的颗粒特征研究
郭浩阳, 彭国峰, 韩爱民, 李 彤, 陈 冬, 程荷兰, 陈 冲, 景 凤
(1. 南京工业大学岩土工程研究所, 江苏 南京 210009; 2. 南京晓庄学院基本建设处, 江苏 南京 211171;3. 江苏省地质矿产局第一地质大队, 江苏 南京 210041; 4. 南京坤拓土木工程科技有限公司, 江苏 南京 210041; 5. 江苏省隧道与地下工程技术研究中心, 江苏 南京 210041;6. 中交隧道工程局有限公司, 北京 100102)
0 引言
碴土是盾构掘进岩层过程中滚刀和围岩相互作用的产物,其几何特性(如粒度、锐度等)与滚刀对围岩的压碎、切削作用有相关性。不同掘进参数下碴土的几何参数存在差异,是利用离散元法研究盾构-围岩相互作用的重要参数。碴土颗粒特征是碴土改良的关键依据,是选择改良剂种类和掺量的重要指标。
对于盾构滚刀切削土体机制,国内外相关人员进行了充分的研究。1963年,R. Teale[1]通过试验发现滚刀刃角是盾构破岩能力的重要影响因素,并提出了用比能来表征盾构的破岩能耗,为之后的盾构刀盘设计和破岩理论的发展奠定了基础。L. Ozdemir等[2-3]提出的CSM模型和孙鸿范等[4]基于线接触理论的滚刀破岩力模型,丰富了滚刀破岩理论研究成果,可用于定量研究掘进参数、围岩力学性质对贯入度等指标的影响。除了对滚刀破岩模式的理论不断进行研究,部分学者还通过试验研究或采用数值仿真的方法对滚刀破岩的机制和性能参数进行了更全面的研究。B. Nilsen等[5]对相同岩石类型的测试和预测结果进行了比较。茅承觉等[6]进行隧洞掘进机盘形滚刀滚压中硬岩石的试验,探索了岩石破碎规律与特点。C. Balci[7]通过全尺寸岩石切割试验来确定隧道掘进机(TBM)的一些设计参数和性能预测。数值仿真方面,Cho等[8]使用AUTODYN-3D通过模拟滚刀破岩并与全尺寸实验室圆盘切割试验进行对比,定量研究了岩石断裂机制并较准确地计算了比能。李娟[9]利用LS-DYNA有限元软件建立了盾构刀具切削土体的模型,对盾构刀具切削过程进行模拟。贾权[10]利用ANSYS/LS-DYNA,按照不同的安装半径和贯入深度对滚刀进行破岩仿真。梁正召等[11]通过采用RFPA2D软件对盘形滚刀作用下岩石破碎机制进行模拟研究。张魁[12]利用UDEC分别对双刃球齿形滚刀和单刃滚刀切割砂岩和节理岩石进行模拟。
目前对盾构碴土颗粒的分析手段主要局限于仿真和模型试验,并未对岩体破碎后的特征进行详细研究。盾构掘进均质岩层时,碴土颗粒直径较大,细颗粒含量较少[13]; 掘进松散地层(砂层、残积土、全风化地层等)时细颗粒含量大、粗颗粒含量较少[14]。复合地层中同时包含了松散地层和岩层,碴土颗粒粒径分布规律不明,掘进参数对碴土颗粒级配的影响更为复杂。本文依托南京宁高城际轨道二期禄口新城南站—铜山站区间盾构隧道工程,对盾构掘进参数与碴样颗粒级配间关系进行了试验分析。
1 碴土颗粒分析
1.1 工程概况

刀盘采用“4辐条+4面板”形式,刀盘直径为6 480 mm,开口率为36%,如图2所示; 配备中心滚刀8具,正面滚刀24具,边缘滚刀13具。滚刀带有高度耐磨的合金齿切削环,刀圈直径为43.20 cm(17英寸)。刀盘2档驱动,Ⅰ档转速0~1.4 r/min,最大转矩为6 219 kN·m; Ⅱ档转速0~2.5 r/min,最大转矩为3 457 kN·m。

图1 盾构区间线路平面图

岩石类型编号饱和单轴抗压强度/MPa完整性指数岩体基本质量指标围岩级别 J31-20 0~0.15100~137.5Ⅴ J31-3r19.380.5283.14Ⅳ J31-3p45.950.32317.85Ⅴ J31-363.350.59437.55Ⅲ—Ⅳ
注: J31-2为强风化凝灰质安山岩; J31-3、J31-3r、J31-3p为中风化凝灰质安山岩。

图2 盾构刀盘主视图
1.2 碴土取样
在盾构掘进过程中,调整推力、刀盘转速等参数,待施工参数稳定后,在输送皮带末端随机取样编号1—9并做好密封措施,取样参数见表2。为了保证盾构正常掘进,盾构的各项掘进参数需要控制在一定范围之内。由于掘进参数动态变化特性,改变的掘进参数会在拟定的掘进参数附近浮动。取样区间为780—835环,取样区间地层断面如图3所示,其中③/④地层面积占比平均值是34%、J31-2是43%、J31-3r是11%、J31-3p是12%。
表2 碴土取样参数
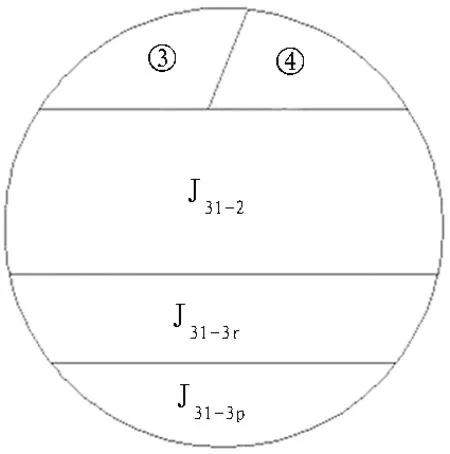
图3 取样区间地层断面图
1.3 碴土颗粒的级配特征
岩石切削碎片如图4所示,碴样充分泡水后滤净改良剂并烘干备用。按筛孔大小排列顺序将碴样按规范要求过筛,筛孔孔径依次为37.5、26.5、19、16、9.5、4.75、2.36、1.18、0.6、0.3、0.15、0.075 mm,筛分后的碴样如图5所示。分别计算分计筛余百分率、累计筛余百分率和各号筛的质量通过百分率并绘制级配曲线,颗粒级配曲线如图6—10所示。地层为风化安山岩地层,实际盾构切削出的岩碴颗粒粒径从0.075 mm 到31.5 mm不等,且安山岩碴样大多运用于公路工程,适用于公路工程集料试验规程。根据JTG E42—2005《公路工程集料试验规程》,在沥青混合料中,粗集料是指粒径大于2.36 mm的碎石、破碎砾石、筛选砾石和矿碴等; 细集料是指粒径小于2.36 mm的天然砂、人工砂(包括机制砂)及石屑。在水泥混凝土中,粗集料是指粒径大于4.75 mm的碎石、砾石和破碎砾石; 细集料是指粒径小于4.75 mm的天然砂、人工砂。由于本工程盾构穿越安山岩地层,而安山岩碎石基本用于沥青混凝土,因此对粗、细颗粒含量分析时以粒径2.36 mm为界。

图4岩石切削碎片
Fig. 4 Rock chipping debris
根据拟定的取样参数,对不同掘进参数下获得的碴土的颗粒级配特征进行分析。由图6可知: 在相对较低的有效推力(9 500 kN)下,刀盘转速从1.5 r/min提升到1.6 r/min,在4.75 mm筛孔孔径以上时,碴样过孔比率基本一致;在4.75 mm筛孔孔径以下时,碴样过孔比率略提高,细粒较多。
由图7和图8可知: 当有效推力一定时(有效推力相对较大),随着刀盘转速的提高,碴样颗粒对应相同的筛径,碴样通过百分率增大,即碴样颗粒变得相对较细。由图7可知: 刀盘转速从1.4 r/min提升到1.5 r/min,在2.36 mm筛孔孔径以下时,碴样过孔比率基本一致;在2.36 mm筛孔孔径以上时,碴样过孔比率大幅提高,细粒增多。刀盘转速从1.5 r/min提升到1.6 r/min时,所有过筛网孔径的碴土比率都提高。由图8可知: 当刀盘转速从1.2 r/min提升至1.6 r/min时,过筛网孔径的碴土比率逐渐提高,细粒含量增多。综上所述,在大推力下,随着刀盘转速的提高,碴土粗颗粒含量不断减少,细颗粒含量不断增多,并且比较低推力情况下的效果明显。

W=16%T=215 mmW=16%T=220 mmW=18%T=202 mmW=18%T=221 mmW=18%T=230 mm

W=18%T=239 mmW=20%T=216 mmW=20%T=229 mmW=20%T=238 mmW=20%T=239 mm
W为含水率;T为坍落度。
图5筛分后碴样颗粒
Fig. 5 Muck sample particles after screening

图6 有效推力为9 500 kN时碴土颗粒级配曲线
Fig.6 Grading curves of muck particles with effective thrust force of 9 500 kN

图7 有效推力为10 000 kN时碴土颗粒级配曲线
Fig.7 Grading curves of muck particles with effective thrust of 10 000 kN
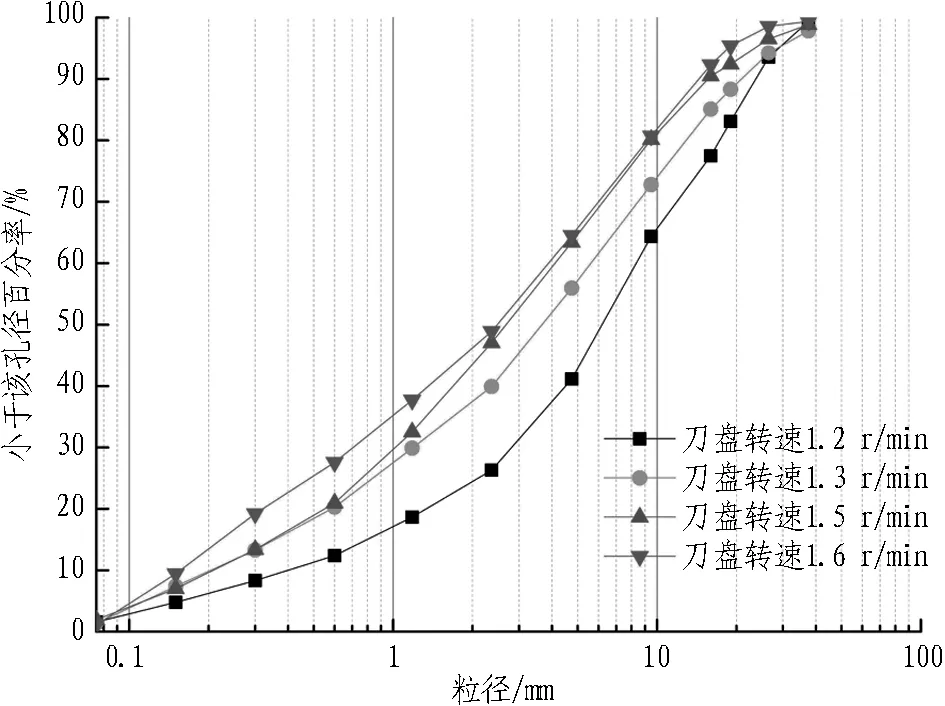
图8 有效推力为12 000 kN时碴土颗粒级配曲线
Fig.8 Grading curves of muck particles with effective thrust of 12 000 kN
图9示出刀盘转速为1.5 r/min时的碴土颗粒级配曲线,图10示出刀盘转速为1.6 r/min时的碴土颗粒级配曲线图。从总体趋势上看,固定的刀盘转速下,盾构推力越大,碴土颗粒就相对越细。
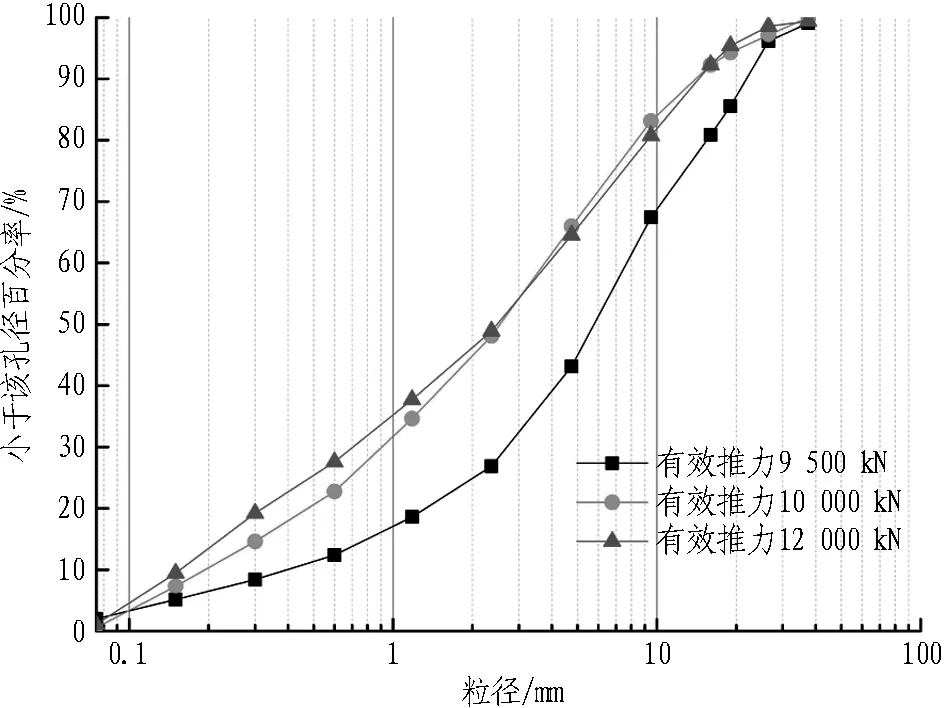
图9 刀盘转速为1.5 r/min时碴土颗粒级配曲线
Fig.9 Grading curves of muck particles with rotation speed of 1.5 r/min
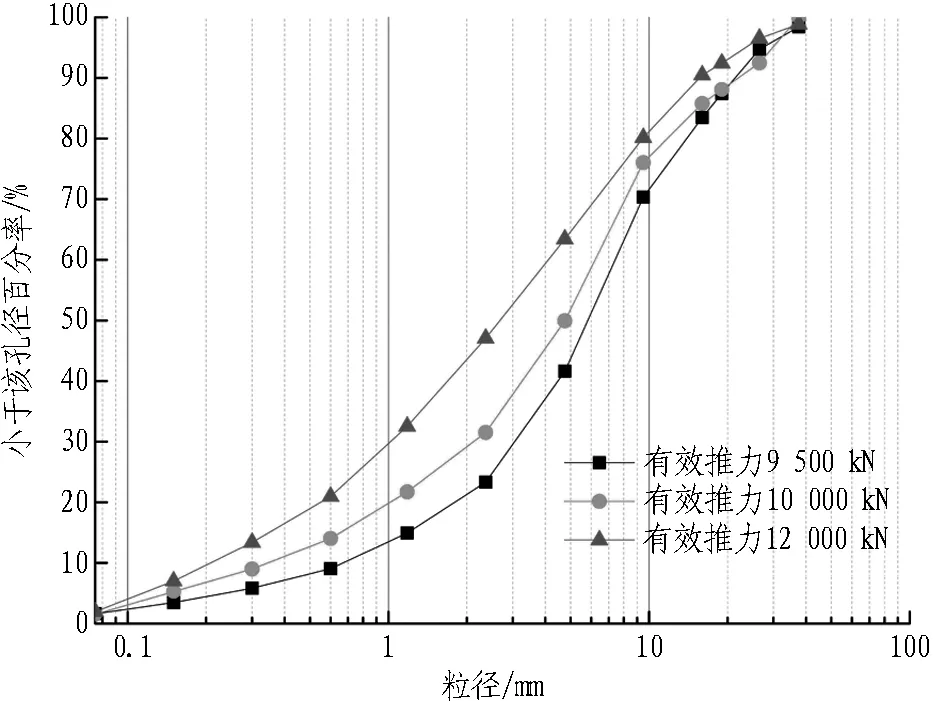
图10 刀盘转速为1.6 r/min时碴土颗粒级配曲线
Fig.10 Grading curves of muck particles with rotation speed of 1.6 r/min
通过对应的掘进参数下碴土颗粒的级配分析可知,盾构有效推力的不断增加,刀盘转速的逐渐加快都会使碴土颗粒逐渐偏小,细小颗粒逐渐增多。由于盾构破岩量和破岩碎片体积存在峰值上限,当盾构正常掘进时有效推力超过围岩破碎所需的推力极限,破岩碎片体积逐渐减小,所以呈现出盾构推力不断增加,碴土颗粒偏细的现象。
1.4 碴土粗、细颗粒含量分析
由于本工程盾构穿越安山岩地层,而安山岩碎石基本用于沥青混凝土,因此根据JTG E42—2005《公路工程集料试验规程》,对粗、细颗粒含量分析时以粒径2.36 mm为界。编号1—9碴样的粗颗粒含量统计见表3,有效推力和刀盘转速与粗颗粒含量关系如图11所示。

表3 碴样粗颗粒含量统计

图11 有效推力和刀盘转速与粗颗粒含量关系曲线
Fig.11 Curves of relationship among effective thrust force, rotation speed and the coarse particle content
由图11可知: 在一定刀盘转速下,有效推力越大,碴土粗颗粒含量越少; 在相同的盾构推力下,刀盘转速越大,碴土粗颗粒含量越少。当有效推力为10 000 kN时,刀盘转速从1.4 r/min增加到1.6 r/min,粗颗粒含量减少26.9%;当有效推力为12 000 kN时,刀盘转速从1.2 r/min增加到1.6 r/min,粗颗粒含量减少30.66%。当刀盘转速为1.5 r/min时,有效推力从9 500 kN增加到12 000 kN,粗颗粒含量减小30.9%;当刀盘转速为1.6 r/min时,有效推力从9 500 kN增加到12 000 kN,粗颗粒含量减小30.1%。并且,随着刀盘转速和盾构推力的不断增加,碴土粗颗粒含量不断减少并最终趋于50%。
2 碴土颗粒级配预测方程分析
2.1 级配方程选用
目前为止,关于岩土颗粒物质几何参数分布累计曲线的数学表述具有相异的适用范围。常用的分布函数有Fuller理想级配方程[15]、Talbot方程[16]、Swamee方程[17]、朱俊高方程[18]和Rosin-Rammler分布函数。将上述分布函数对各组碴样的级配曲线进行拟合,结果如图12所示。根据拟合结果可以得出,除Fuller理想级配方程和Talbot方程外,其他公式都能很好地反映碴土颗粒级配特征曲线。但由于Swamee公式对双曲线型的级配特征曲线和直线型的级配特征曲线都不能准确描述,朱俊高提出的公式中颗粒最大粒径为确定的常数,而实际盾构掘进过程中无法得知土舱内破碎岩块的具体粒径,因此只适合对已知粒径范围的颗粒进行分析; 而Rosin-Rammler分布函数中的粒径d可以进行预设,本身为变量,因此Rosin-Rammler分布函数更加适用于盾构破岩颗粒级配特征分析。Rosin-Rammler分布函数的表达式如下:
G=[1-exp(-adn)]×100%
。
(1)
式中:G为累计百分数;a为绝对常数,a=1/De,其中De为特征粒径,能反映颗粒粗细程度,De越大土体颗粒越粗,反之则越细;d为粒径;n为均匀性指数,反映颗粒级配范围的宽窄程度,n越大颗粒级配的范围越窄,反之则越宽。
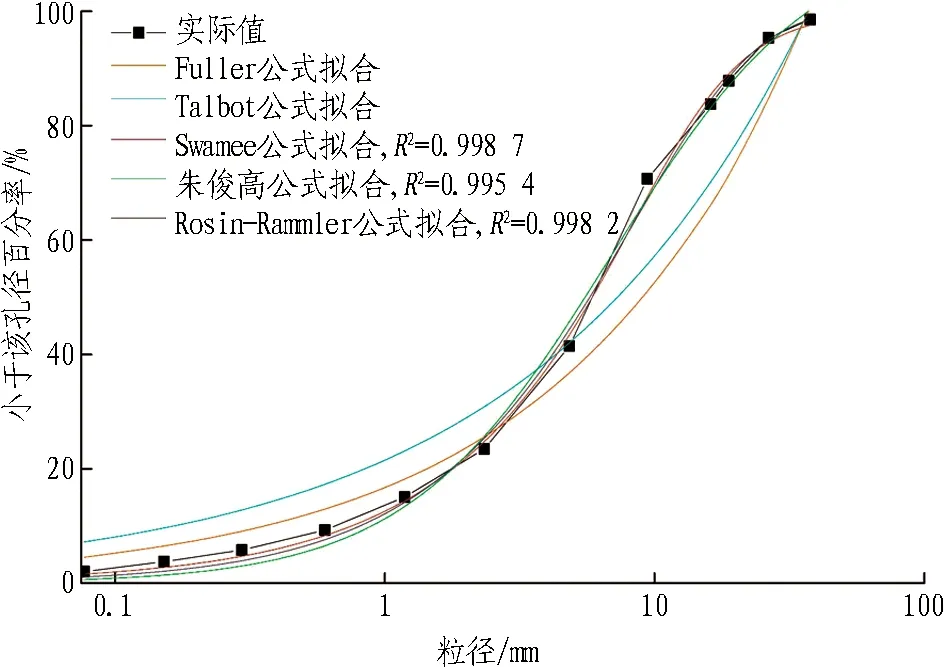
图12 公式拟合结果曲线
利用Rosin-Rammler分布函数对9组碴样级配方程拟合的结果见表4。

表4 Rosin-Rammler分布函数拟合结果
2.2 级配方程与掘进参数关系分析
采用SPSS软件对Rosin-Rammler分布函数中的绝对常数a、均匀性指数n与有效推力T、刀盘转速v进行多元非线性回归计算,得到级配方程系数预测模型如式(2)—(3)所示,绝对常数a和均匀性指数n的多元回归拟合结果的相关系数分别为0.91和0.92,且显著水平均小于0.05。
;
(2)
。
(3)
为了更好地描述单一因素对方程绝对常数a、均匀性指数n回归模型的影响情况,通过对有效推力T和刀盘转速v求一阶偏导数,即对T求偏导数时,对刀盘转速v赋值,分析有效推力T的变化对绝对常数a和均匀性指数n的影响; 同理,对v求偏导数,对T赋值。
1)T=12 MN,则有:
(4)
。
(5)
2)v=1.6 r/min,则有:
(6)
(7)
运用Origin绘图软件对式(4)—(7)进行绘图,定义T和v的定义域分别为[9.5,12]和[1.2,2],结果如图13和图14所示。
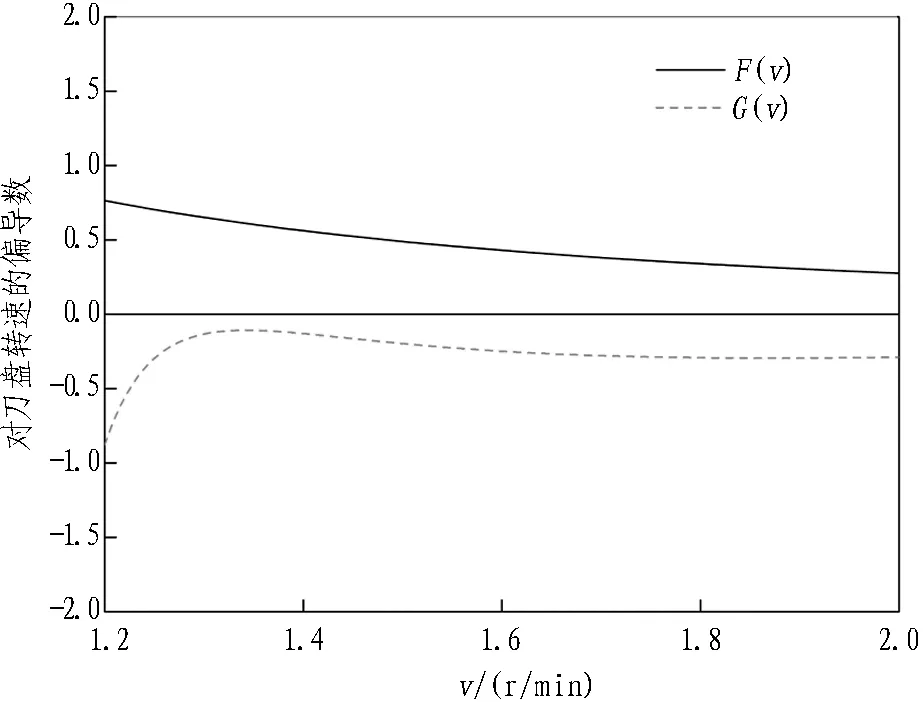
图13 固定推力下刀盘转速与方程系数的关系曲线
Fig.13 Curves of relationship between rotation speed of cutterhead and equation coefficient under fixed thrust force
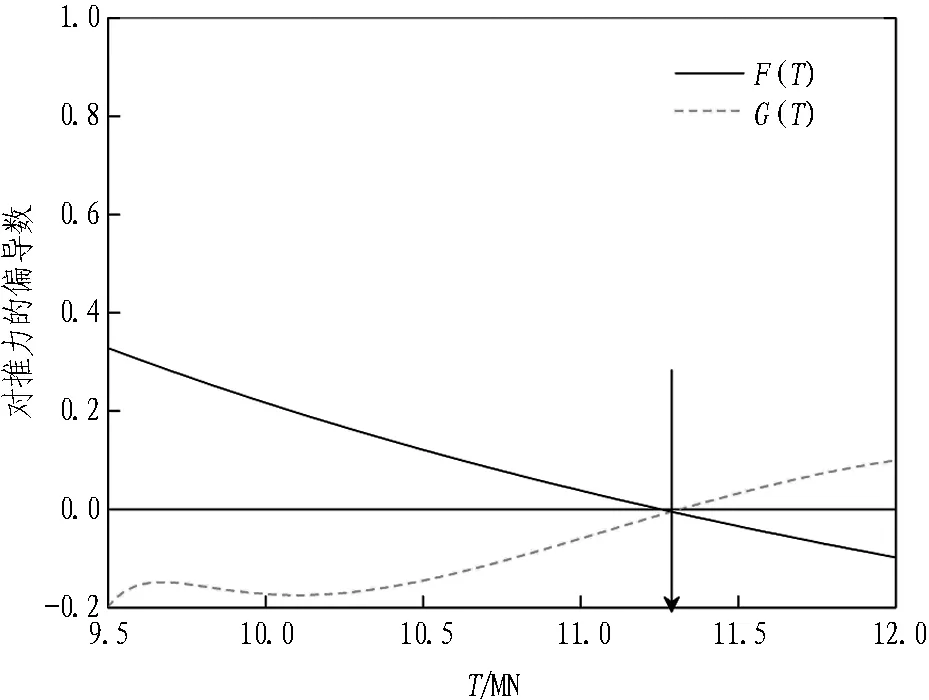
图14 固定转速下推力与方程系数的关系曲线
Fig.14 Curves of relationship between thrust force and equation coefficient under fixed rotation speed
由图13可知,在当有效推力为固定值时,绝对常数a和均匀性指数n对刀盘转速v所求的偏导数在定义域范围内分别大于0和小于0,由此可知式(2)在设定的定义域范围内单调递增,式(3)在设定的定义域范围内单调递减。即在固定推力情况下,绝对常数a随着刀盘转速v的增加而增大,均匀性指数n随着刀盘转速v的增加而减小。这就表明刀盘转速越大,碴土颗粒分布范围越宽;同时,与绝对常数对应的特征粒径De越小,碴土颗粒越细。
由图14可知,当刀盘转速一定时,偏导函数F(T)和G(T)在当T≈11.3 MN时有零点。因此可知式(2)所对应的函数在推力区间[9.5,11.3)和(11.3,12]分别呈单调递增和单调递减,同理可知式(3)所对应的函数在推力区间[9.5,11.3)和(11.3,12]分别呈单调递减和单调递增。绝对常数a随着T的增加先增大后减小;均匀性指数n随着T的增加先减小后增大。与2.3节和2.4节中得出的结论相对比,可看出T∈(11.3,12]时,针对级配方程参数n提出的预测模型超出了其适应性,体现了统计学模型在计算适用性上存在局限。所以,针对级配方程参数n提出的预测模型在T∈[9.5,11.3)时可靠性和准确性较高,在T∈(11.3,12]时预测结果误差较大。绝对常数a总体上随着盾构有效推力T的增加而增大,碴样特征粒径越小,碴土细颗粒增多;均匀性指数n总体上随着盾构有效推力T的增加而减小,碴样粒度分布范围越宽,碴土细颗粒增多。
3 结论与讨论
1)盾构破岩量和破岩碎片体积存在峰值上限。盾构有效推力的不断增加,刀盘转速的逐渐加快都使得碴土颗粒逐渐偏小,细小颗粒逐渐增多。有效推力越高,增加刀盘转速导致细颗粒占比增加越显著。
2)Rosin-Rammler分布函数对盾构碴土颗粒级配曲线实测段拟合精度较高,能够在颗粒粒径上下限未知的情况下较好地预测不同掘进参数下的碴土颗粒级配。
3)盾构碴土颗粒级配方程系数的预测模型对不同掘进参数下的级配方程系数预测精度较高。级配方程绝对常数a与v、T均为正相关; 而均匀性指数n的预测模型在T∈[9.5,11.3)时可靠性和准确性较高,在T∈(11.3,12]时预测结果误差较大。
本文定量统计分析了复合地层中不同掘进参数下碴样的颗粒特征,而不同地质条件下的碴土颗粒级配分布规律仍有待后续研究。统计学方法能够在一定程度上量化工程经验,但仍存在适用性局限,需要进一步研究统计学方法和理论分析相结合的盾构破岩规律分析方法。可以把基于实测并量化的碴土级配和碴土改良工艺参数间的经验关系,和掘进参数和颗粒级配特征之间的经验关系相结合,进一步开展碴土改良工艺参数预测和优化研究。

