利用柯尼希定理巧解质点系的相对速度问题

郑 金

(辽宁省凌源市职教中心,辽宁 朝阳 122500)

力学中的柯尼希定理反映了质点系的总动能的组成种类及其数量关系,即质点系的总动能等于质心的动能与各质点相对于质心运动的动能之和,在二体问题中质点系的动能等于质心动能与相对动能之和.可以证明,在质心参考系中,两个物体的相对动能等于折合质量与相对速度平方的乘积的一半.对于相互作用的两个物体的相对运动问题可有多种解法,但利用柯尼希定理来解答,可化繁为简.

图1

例1.如图1所示,在光滑的水平面上,两个物体A和B的质量分别为m1和m2,中间用一根劲度系数为k的轻弹簧连接在一起.开始时两个物体静止,弹簧处于自然状态,现给物体A一个向左的初速度v0,弹簧始终处于弹性限度内,求两个物体运动的相对位移为x时的相对速度为多大?

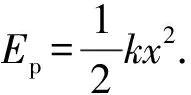
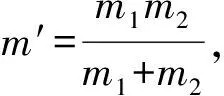
由于系统在水平方向不受外力,因此系统质心的速度保持不变,对系统由动量守恒定律有

m1v0=(m1+m2)vC，

根据柯尼希定理可知两个物体的总动能为

Ek=Ek′+EkC.

对系统由机械能守恒足律有Ek0=Ek+Ep.联立方程可得相对速度大小为

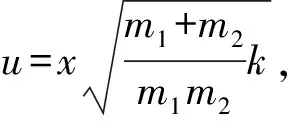
例2.质量分别为m和M的两个物块A、B用橡皮绳相连,放在水平台面上,橡皮绳原长为a,当它伸长时,如同劲度系数为k的弹簧.物块与台面之间的动摩擦因数为μ,现将它们拉开,距离为b(b>a),然后由静止释放,求两物块相碰时的相对速度.

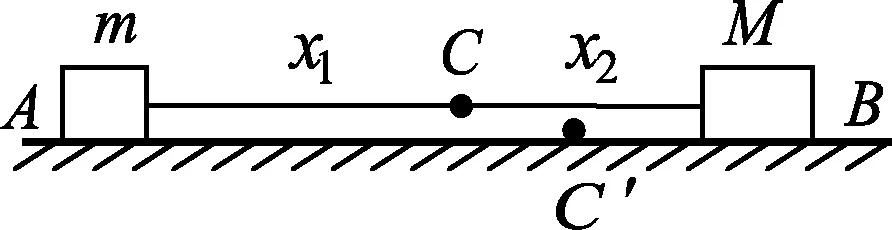
图2

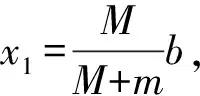
两个物块逐渐靠近,受到的摩擦力方向相反,考虑到二者质量不等,设m

W2=-f1(x1+x)-f2(x2-x)=

对系统由动能定理和柯尼希定理得

W1+W2=Ek′+EkC，

解得

点评:解题关键是确定系统的质心刚开始时的位置和相碰时的位置在何处并画出示意图,这样在计算摩擦力做的功时才能确定对应位移的大小和方向,同时还要考虑摩擦力的方向.设置的质心位移x是未知量,在解方程时消去了.如果在地面参考系中认为系统的质心静止不动,则不必对系统的质心应用动能定理,而且在计算摩擦力对系统做的功时也不需考虑质心的位移,虽然所得结果相同,但运动情况却与实际不符.因为由质心运动定理可知,在恒力作用下系统的质心做匀加速运动,不可能静止,除非两个物体的质量相等.

对系统由动能定理和柯尼希定理有

W1+W2=Ek′+EkC，

解得

例3.在光滑水平面上有两个物体A、B,其质量分别为m1、m2,它们沿同一直线运动并发生碰撞.碰撞前A、B的速度分别为v1、v2,碰撞后的速度分别为v1′、v2′,试分析v1′、v2′满足什么关系时,碰撞过程中损失的机械能最大?

(a12+a22+…+an2)(b12+b22+…+bn2)≥(a1b1+a2b2+…+anbn)2，

需将末动能的关系式变形为

由柯西不等式可知

(m1+m2)(m1v1′2+m2v2′2)≥

(m1v1′+m2v2′)2.

由动量守恒定律有

m1v1+m2v2=m1v1′+m2v2′，

这表明,只有当二者碰撞后同速,即碰撞后粘在一起时,系统损失的动能最大.

点评:解题关键是掌握数学中的柯西不等式,利用数学知识解决物理问题,难点是把由物理量组成的多项式变换为符合柯西不等式的形式.

解法2:利用柯尼希定理.对于在光滑水平面上沿同一直线运动的两个物体,由于系统受到的合外力为0,则系统的质心做匀速直线运动,那么质心的动能保持不变,根据柯尼希定理可知,碰撞后的动能等于系统的质心动能与两个物体的相对动能之和,因此只有当相对动能为0时,系统的动能才最小,即系统损失的动能最大,而此时相对速度为0,即发生了完全非弹性碰撞.所以说当发生完全非弹性碰撞时系统损失的机械能最大.

综上可见,利用柯尼希定理解答质点系的相对速度问题不仅能化繁为简,还可拓展解题思路,既有助于加深理解知识,又可训练思维能力,可谓一举多得.