基于银行账户亲密度网络推理的团伙预测研究

吕芳，陆海博，王巍，黄俊恒，王佰玲

基于银行账户亲密度网络推理的团伙预测研究

吕芳，陆海博，王巍，黄俊恒，王佰玲

（哈尔滨工业大学（威海）计算机科学与技术学院，山东 威海 264209）

近年来，针对涉众型非法金融活动在资金交易规律的研究引起了研究者的高度关注。为解决利用银行交易数据进行异常账户犯罪团伙主动发现的问题，提出一种基于银行账户非对称亲密度网络的团伙预测方法。首先，建立银行账户交易通用网络模型，将时序交易数据嵌入网络结构中。然后，利用节点的直接和间接交易关系信息，提出一种账户非对称亲密度计算方法。最终，利用节点在亲密度网络上的非对称交互信息，得到节点的异常倾向性指标。在包含传销团伙的真实数据上的实验结果表明，基于亲密度网络的团伙预测方法能有效发现潜在传销人员。

银行账户交易网络；亲密度网络；直接亲密度；间接亲密度；团伙预测

1 引言

涉众型非法金融犯罪活动呈现涉案人数多、涉案资金量大的特点，严重影响国家经济和人民的财产安全。在金融犯罪活动中，犯罪分子需要利用银行等金融机构，将非法所得的资金经过一次或多次交易，汇聚到最终账户中。图1为非法传销和非法洗钱金融犯罪活动的交易关系示例。此类犯罪活动组织中成员的角色分工呈类金字塔形或纺锤形等结构，相应账户的资金交易由其扮演的角色驱动产生，使犯罪关系极其隐蔽。目前，银行部门使用的反洗钱等金融安全系统能够根据交易规则发现存在异常交易的单个账户，但对上述多账户协作实施非法金融活动的行为束手无策。例如，非法传销活动，它是一种由一组人员操纵的以上线发展下线、吸纳下线会员费为欺诈方式的涉众型金融犯罪活动。如图1(a)所示，其资金交易关系具有明显的金字塔层级结构，底层为会员节点，中间层为初级上线节点，顶层为操纵节点。会员节点通过缴纳会费加入组织，初级上线节点从下线会员的会费抽取提成获得收益，剩余资金全部沉淀入操纵节点的账户中。可见，在非法传销活动中，资金从受骗群众流向底层小头目，再汇集到重要头目。对于线下传销而言，这种资金的转移过程大部分是通过银行账户交易完成的。

涉众型非法金融活动的交易关系复杂，交易规模较大，增加了犯罪行为的隐蔽性，使侦查人员全面打击犯罪组织的任务越来越棘手。已知部分涉案成员，利用成员之间关系的紧密程度主动发现嫌疑账户，能有效解决犯罪团伙成员预测问题。

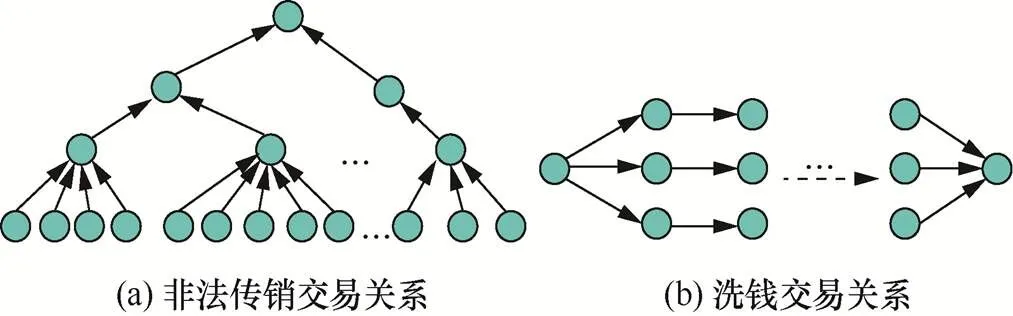
图1 涉众型非法金融活动交易关系示例

近年来，在金融安全领域，通过构建金融网络模型，利用社交网络分析技术挖掘犯罪信息的研究引起了研究者的重视。陈鹏等[1]采用网络建模的方法研究不同类型犯罪组织的结构特性，基于复杂网络建模的方法建立具有层次特征的犯罪组织网络，考察了层次组织结构的运行效率和安全性。在金融网络的构建方面，为了分析资金网络的内部拓扑结构，刘晋霞等[2]分别定义了账户节点和资金账户关系，进而提出一种有向加权的资金融通网络构建方法。韩华等[3]基于随机矩阵理论，改进金融网络相关系数矩阵生成方法，构建了金融网络模型，获得了更加紧密的网络结构。在反洗钱的应用研究中，为了解决需要兼顾时间、成本、流量、风险等多因素的多目标优化问题，李琼婕等[4]提出了基于最小费用最大流的扩展模型。总体来说，当前的研究集中在利用各种类型的历史数据构建犯罪网络，将组织关系嵌入网络结构中。但是，上述网络构建方法多针对特定应用且依赖多种信息源，可扩展性较弱。此外，量化网络节点关系的信息粒度过粗，导致用于同伙关系预测时的准确性较低。本文研究如何利用银行账户的交易日志数据量化账户之间的关系强度，实现同伙预测的方法。

本文使用的账户交易日志数据如图2(a)所示，包含交易时间、交易对手、交易金额及交易方向等信息。因此，可据此构建账户的有向、加权交易网络，其中节点的局部拓扑结构如图2(b)所示。

图2 银行账户交易数据示例

可见，账户之间资金的往来是评判实体之间关系程度的重要标准。显然，日志数据中账户之间交易的金额、频率、周期性、交易网交集等信息是这种关系的具体体现。账户之间关系的紧密程度（本文称作账户亲密度）是评估账户所关联实体亲密程度的重要标准之一。

本文首先建立资金交易网络模型，将时序交易数据嵌入网络结构及网络关系中。由上述分析可知，网络中节点间的关系强度与节点的交易信息和局部拓扑结构紧密相关。本文首先定义了单向信任度，从资金交易的角度计算节点间的直接亲密程度；然后从局部拓扑结构的角度，将节点间的间接交易关系进行分类，提出一种节点间的间接亲密度计算方法。综合上述两种亲密度指标，本文计算任意节点对的综合亲密度，构建得到一个非对称亲密度网络。亲密度网络中的节点为银行账户集合，有向边表示节点的单向关系，边的权重为单向关系的综合亲密度。基于上述全连通、非对称的亲密度网络，在已知部分嫌疑节点的前提下，本文提出一种犯罪团伙预测方法。在包含传销团伙的银行账户交易数据上的实验结果，证明了该方法发现潜在传销账户的有效性。

2 相关工作

银行账户亲密度计算可以归类为网络中的节点相似性计算，这方面的研究基本上可以分为以下两类。

1) 基于网络拓扑结构的节点相似性计算。该类算法根据考虑的节点信息种类的差异可分为3种。第一种算法只考虑直接邻居信息、同时考虑间接邻居信息及另外考虑路径信息。节点的直接邻居信息主要包括共同邻居的数量、节点度数、节点之间的连接程度[5-6]，具有计算复杂度较低、适用范围广的特点。第二种算法同时计算了直接和间接邻居对节点关系的影响，其中参与计算的因素包括一阶邻居信息、二阶邻居信息以及多阶邻居信息[7-8]。随着考虑邻居节点层数的增加，算法的计算复杂性逐次增大。第三种算法在邻居信息的基础上，结合了路径强度、连通程度等信息[9]。这种方式时间复杂性高，在大规模网络上应用时间开销很大。

2) 网络表示学习节点相似性计算。近年来，受自然语言中词向量生成技术的启发，网络节点向量生成技术的研究引起了学者的重视。Perozzi 等[10]提出DeepWalk算法，首次将网络表示学习技术引入网络分析领域。随后，针对大规模有向带权图的网络表示学习问题，Tang等[11]提出一种对所有一步和二步邻居节点进行概率建模的LINE方法。Wang等[12]提出SDNE方法使用深层神经网络对节点间的非线性建模。为学习网络结构的相似性，Donnat等[13]提出一种名为GraphWave的可扩展无监督网络表示学习方法。

以上两类节点相似性计算方法利用的仅为网络节点的局部拓扑结构信息。不同于传统网络，金融网络中，账户节点之间丰富的时序交互信息对量化账户的亲密度尤其重要。基于此，本文在局部拓扑结构信息的基础上，融入节点交互信息，提出一种非对称亲密度网络构建方法。

在涉众型金融犯罪活动中，根据已知犯罪线索、犯罪嫌疑人预测犯罪团伙的研究，受到许多研究者的关注。在组织成员预测方面，Sun等[14]改进了中心节点计算方法，利用节点之间的可信度，提出了一种限制连接节点集合的搜索空间，进而识别协作伙伴的方法。在犯罪网络应用方面，Chen等[15]针对犯罪集团的组织特点，结合共犯网络结构分析和数据挖掘技术，对组织犯罪集团进行系统分析和挖掘研究。针对组织成员的上下级支配关系，杨莉莉等[16]提出了一种犯罪组织成员关系挖掘方法；高建强等[17]结合聚类分析与社会团伙技术，提出一种组织成员发现模型。李万彪等人[18]提出了一种基于关系数据模型的犯罪网络挖掘方法，该方法可以挖掘已知嫌疑人、未知嫌疑人及深层的犯罪团伙关系。在解决从历史犯罪案宗数据中挖掘组织成员的任务中，唐德权等[19]提出一种使用层次聚类技术进行同组人员发现的方法。总体来说，上述犯罪网络的数据源类型多为历史案宗数据，与本文使用的交易日志数据不同。此外，进行组织成员预测时，主要依据关联网络的拓扑结构信息。本文在亲密度网络的基础上，综合考虑节点对的非对称亲密度和局部交易关系，得到了节点的异常倾向性指标，进而实现犯罪团伙预测。

3 银行账户交易网络数学模型

银行账户交易网络是一种超大型且动态变化的复杂网络。账户间的交易具有有向、有序、金额和频度等属性，上述交易特点导致账户间具有复杂的关联关系。基于账户间的关系特点，本文建立了银行账户交易网络数学模型。银行账户用网络节点表示，账户间的交易关系用节点之间的有向边表示，有向边的权重表示交易时间、金额、次数等信息。银行账户交易网络数学模型见定义1。

定义1 一个银行账户交易网络可表示为= ()，其中={1,2, … ,v}为账户集合，= {e} ⊂×, 1≤,≤为边集合，v与v之间存在有向边当且仅当v对v至少进行了一次交易，该有向边记作e= <v,v>。= {w},∈(R),w= ((1),(2), … ,()), 其中，(),N分别表示节点v与v间第次交易的金额和总交易次数。

4 非对称亲密度网络

在定义1中的银行账户交易网络中，节点之间的有向边权重W包含了账户之间交易信息，这些信息隐含了账户之间的亲密程度。本文基于两点之间的交易信息和局部拓扑结构，提出了账户亲密度计算方法，构建了银行账户的非对称亲密度网络。

4.1 信任度

在现实生活中，甲转给乙一笔钱，显然甲在一定程度上信任乙，随着甲对乙交易次数和金额的增加，表明甲对乙的信任程度逐渐增加。在资金交易中的信任度是单向的，简单来说，甲给乙钱，表明甲信任乙，反之并不成立。甲对乙的信任程度主要随两个因素变化。1）交易金额：甲对乙的交易金额越大，说明甲对乙的信任度越高。2）交易次数：甲对乙的交易次数越多，说明甲对乙的信任度越高。基于这两点，本文提出了账户对账户的信任度计算方法。

设m是账户对账户的交易资金总额，n是对的交易次数，那么对的信任度可以表示为m和n的函数。本文提出式(1)用于计算对的信任度。

同理：设m是对的交易资金总额， n是对的交易次数，那么对的信任度由式(2)计算。

4.2 直接亲密度计算

式(1)和式(2)分别计算了对的信任度和对的信任度，双方互信程度的均值体现了双方的亲密程度，本文称为直接亲密度。和的直接亲密度可用式(3)计算。

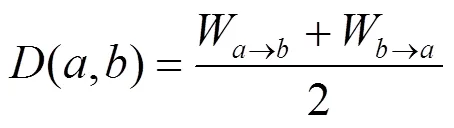
4.3 间接亲密度计算

在资金交易网络中，尤其在犯罪团伙之间，账户之间除直接交易外还可能存在多种不同的间接交易。所以，在亲密度的计算中，虽然直接交易的影响占主导地位，但某些间接交易对账户的亲密度也有较大的影响。间接交易信息反应在账户在交易网络上的局部拓扑结构中。基于此，除直接亲密度外，本文考虑账户之间的间接亲密度。

在金融网络中，节点之间往往具有复杂的交易关系。例如，在图3中，节点、之间不但具有直接的交易关系，同时由于各自节点局部拓扑结构的交集，产生了间接交易关系。这些复杂的间接交易关系同样体现了和的亲密性。本文将间接交易情况简化为两类。第一类如、、之间的交易关系，即交易给，交易给，因此可以理解为是和之间的媒介，与的亲密性也因为的存在而有所增加。第二类为2个账户具有共同的转账邻居。如图3所示，和都有转账给的情况；或者，具有转账给和的情况，可以理解为和拥有共同的朋友。随着共同朋友数量的增多以及二者与共同朋友的亲密程度的增加，和的亲密程度也在增强。基于以上分析，本文提出了账户之间的间接亲密度计算方法。

图3 账户交易示意

节点与节点的间接亲密度可由式(4)计算。

4.4 综合亲密度

综合直接亲密度和间接亲密度，本文提出了账户之间的综合亲密度（以下简称亲密度）计算方法，如式(5)。

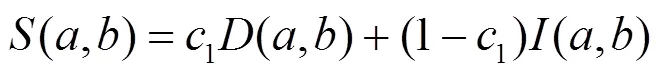
其中，1, 11为直接亲密度和间接亲密度对亲密度的贡献系数。

通过计算任意两点的亲密度，本文建立了银行账户亲密度网络，见定义2。

定义2 给定银行账户交易网络()，对应的非对称亲密度网络为’(,,)。其中，={v,v, … ,v}为账户集合，= {o} ⊂×, 1≤,≤为边集合，任意v与v之间存在有向边，该有向边记作o= <v,v>。= {S},S∈[0,1] 是由节点到由式(5)计算的单向亲密度。

5 团伙预测算法

账户亲密度网络反映了账户之间的亲密程度，如果一个待测账户与多个犯罪账户亲密度值很大，则有理由相信账户在一定程度上是涉案账户。针对待测账户是不是涉案账户，本文主要考虑两个因素：1）与已知涉案账户的亲密度值；2）邻居节点中涉案账户的数量。

假设已标记涉案账户集合为C，()为待测节点在中的邻居集合，则账户的涉案程度可由式(6)计算。

其中，𝛼，𝛽∈[0,1]为权重系数。() ∈[0,1]的大小反映了待测节点的涉案程度。

6 实验与结果分析

6.1 实验环境

本文实验硬件环境为Inter(R) Core i7-7700HQ CPU@ 2.80 GHz，内存(RAM) 16 GB。软件环境为Python语言，Ubuntu 18.04 LTS操作系统。

6.2 实验数据

近几年，笔者积极参与经侦部门打击非法传销的工作，曾参与辅助侦查多起线下传销案件。本文使用的两份数据集均为包含传销组织的银行账户交易日志数据，每条日志数据包括交易双方账户、交易方向、交易时间、交易次数和交易金额等属性。数据经过去重、去噪、脱敏等处理后，用于对本文算法的测试。数据集1中包含交易记录349 126条，涉及8 384个银行账户。其中，传销账户883个，正常账户7 501个，在资金交易网络中有向边共14 646条。数据集2中涉及5 872个银行账户，其中119个传销账户。将数据集1按照4:1的比例划分训练集和测试集，得到包含662个传销账户和5 626个正常账户的训练集。从数据集2选择319个节点作为测试集，其中包含200个正常账户和119个传销账户。

6.3 参数设定

统计发现，数据中两个账户之间交易金额总和的最大值为1 836.61万元，两个账户之间的交易次数总和最大值为1 008次。通过数据分析，发现金额小于100元的交易，基本为水电费等噪声数据，因此本实验将小于100元的数据进行了过滤。经过多次实验验证，标准化处理函数(),()和式(1)~式(5)的各项系数采用如下设置时，取得较好的实验结果。

表1 节点对的亲密度指标示例

6.4 亲密度算法分析

为了验证亲密度算法的准确性，本文选取了9组具有亲密度值的账户对信息（交易金额、交易次数、共同对手、间接路径的数目）来分析间接亲密度和直接亲密度是否与账户对之间真实的紧密程度一致。实验结果如表1所示。

在现实交易场景中，交易金额、交易频次、共同交易对手、间接交易方式都会影响交易双方的亲密关系。由表1的第1、2条记录可知，在间接属性相近的情况下，账户对的交易金额、交易频次越高，两节点越亲密；同理，由第6、7条记录可知，在直接属性相近的情况下，账户对的共同交易对手数量、间接路径条数越多，两节点越亲密。上述亲密度结果分别证实该指标的取值与真实交易场景下的亲密关系一致。如第2、4条记录所示，在间接属性相近的情况下，交易频次的差异引起了亲密度指标的较大变化。这种变化与现实场景中直接属性比间接属性更能反映节点对亲密度的情况一致。因此，本文的综合亲密度计算方法能够相对准确地反应账户之间的亲密关系。

6.5 团伙预测结果分析

在数据集1进行训练得到()（见式(6)）的最优参数取值。经过50次实验的平均结果发现，当()的系数采用=1，=0.018 7时，算法在测试集上取得最好的团伙预测效果。测试集上的实验结果如图4~7所示。

如图4所示，算法的准确率随取值的增加呈增大趋势，且当()的取值大于0.4时，准确率趋于稳定，最高达到95.3%。反之，算法的召回率（如图3所示）随着值的增大呈逐渐降低的趋势。可见准确率和召回率呈负相关，两者的关系如图6所示。随着值的增加，算法的1值呈先急剧增大后平稳下降的趋势，且当值取0.1附近值时，1值达到最优。

图4 准确率随H值变化

图5 召回率随H值变化

图6 准确率和召回率的关系

图7 F1值随H值变化

当()的参数选择最优的情况下，在数据集2上进行算法准确性测试。实验结果如混淆矩阵所示。随机选择119个传销账户中的69个作为已知标记数据，对剩余账户的标签进行预测。在该数据集上的准确率达到85.6%，此时的混淆矩阵如图8所示。

6.6 团伙预测对比分析

本文分别选取交易金额、交易频次、直接亲密度的预测算法作为同伙预测的单因素依据，与本文提出的基于综合亲密度的同伙预测方法进行对比分析。在数据集1上的团伙预测性能实验结果如表2所示。

表2 预测算法对比分析

如表2所示，本文基于综合亲密度的团伙预测方法取得了最优的准确率、召回率和1值。基于直接亲密度的算法同时包含交易金额、频次信息，取得了优于单因素的预测性能，证明了两种交易信息存在互补关系。本文算法在直接亲密度基础上结合节点的局部拓扑信息，进一步提高了预测性能，证明了交易关系信息对预测传销团伙的必要性。上述4种算法的ROC曲线如图9所示。

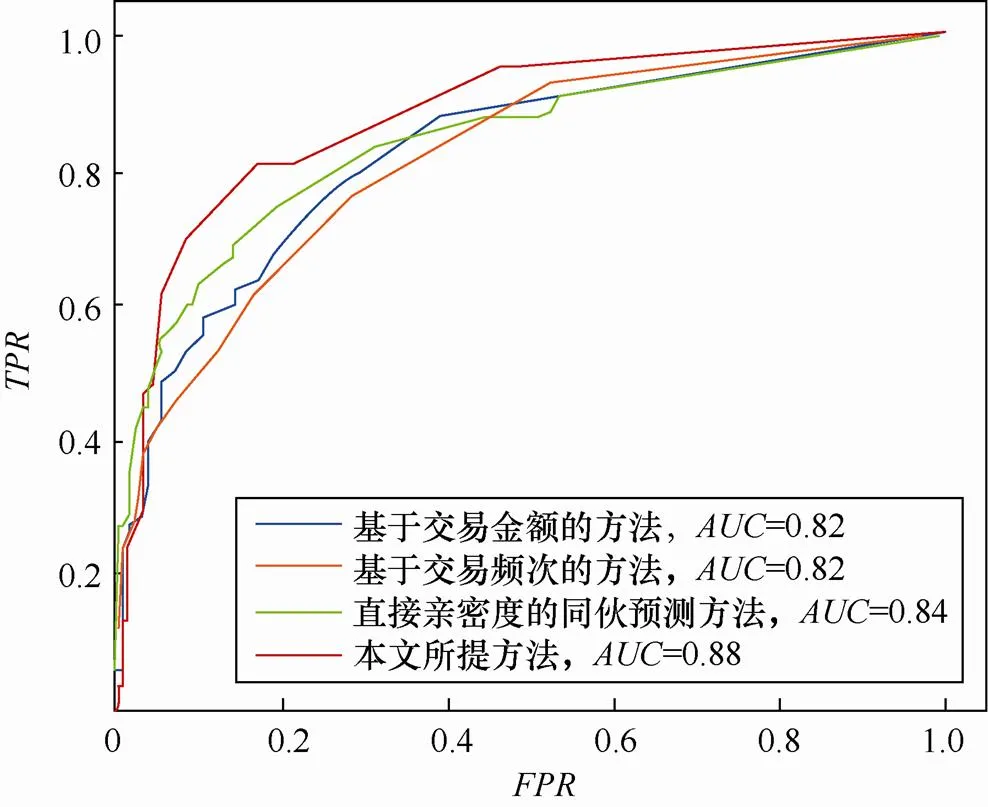
图9 4种算法的ROC曲线

可见，本文方法持续优于另外3种方法。该实验结果，再一次验证了共同使用直接亲密度和间接亲密度进行同伙预测算法的有效性。

7 结束语

本文利用银行账户交易数据，在犯罪团伙预测方面进行了尝试。在建立了银行账户交易网络模型的基础上，提出一种非对称亲密度网络构建方法。本文同时考虑了账户节点的直接交易信息和局部拓扑关系信息，量化生成任意节点对的单向综合亲密度。进而，利用节点在银行账户交易网络中的关系子图和亲密度网络与异常节点的亲密程度，进行节点的同伙预测。在包含传销异常账户的真实资金交易数据上的实验结果，验证了本文定义的亲密度指标能够准确描述团伙资金交易的特点，提出的团伙预测方法能有效发现潜在犯罪嫌疑人。

在实验中发现，由于交易环境复杂，账户对之间的交易信息浮动较大，如交易次数从0到1 000，交易金额从100元到1000多万元。因此，如何平衡交易次数和交易金额对亲密度的影响、如何平衡各种邻居节点对亲密度的贡献、如何平衡直接亲密度和间接亲密度的权重，需要大量数据的支撑。由于本实验数据的局限性，实验获得的平衡系数可能存在偏差。这是下一步本团队需要改进和继续研究的工作。

另外，采用网络表示学习方法，把节点进行量化处理，然后度量节点关系和拓扑结构挖掘的研究逐渐引起研究者的重视。利用这种机器学习的方法进行亲密度计算和犯罪团伙预测的研究也是下一步工作的重点之一。

[1] 陈鹏, 袁宏永. 犯罪组织结构的社会网络分析[J]. 清华大学学报(自然科学版)，2011, 51(8): 1097-1101.

CHEN P, YUAN H Y. Social network analysis of crime organization structures[J]. Journal of Tsinghua University (Science and Technology), 2011, 51(8): 1097-1101.

[2] LIU J X. The research on detecting community structure of complex networks and its application in financial Networks[D]. Lanzhou: Lanzhou University of Technology, 2013.

[3] 韩华, 吴翎燕, 宋宁宁. 基于随机矩阵的金融网络模型[J]. 物理学报，2014, 63(13): 431-440.

HAN H, WU L Y, SONG N N. Financial networks model based on random matrix[J]. Acta Physica Sinica, 2014, 63(13): 431-440, 2014.

[4] 李琼婕, 薛耀文. 最小费用最大流维度拓展及其在反洗钱中的应用研究[J]. 山西师范大学学报（自然科学版）, 2014, 28(1): 28-32.

LI Q J, XUE Y W. Dimension-expansion of minimum cost and maximum flow theory and its application research in anti-money laundering[J]. Journal of Shanxi Normal University (Science and Technology), 2014, 28(1): 28-32.

[5] ADAMIC L A, ADAR E. Friends and neighbors on the Web[J]. Social Networks, 2003, 25(3): 211-230.

[6] WU Z H, LIN Y F. Link prediction with node clustering coefficient[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 452: 1-8.

[7] ZHOUT, LYU LY, ZHANG YC. Predicting missing links via local information[J]. The European Physical Journal B, 2009, 71(4): 623-630.

[8] LEICHT E A, HOLME P, NEWMAN M E J. Vertex similarity in networks[J]. Physical Review E Statistical Nonlinear and Soft Matter Physics, 2006, 73(2): 1-10.

[9] ZHU X Z, TIAN H, CAI S M. Predicting missing links via effective paths[J]. Physica A: Statistical Mechanics and Its Applications, 2014, 413(11): 515-522.

[10] PEROZZI B, RAMI A R, SKIENA S. DeepWalk: anline learning of social representations[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (SIGKDD’14). 2014, 701-710.

[11] TANG J, QU M, WANG M, et al. LINE: large-scale information network embedding[C]//International Conference on World Wide Web (WWW’15).2015:1067-1077.

[12] WANG D X, CUI P, ZHU W W. Structural deep network embedding[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (SIGKDD’16).2016:1225-1234.

[13] DONNAT C, MARINKA Z, HALLAC D, et al. Learning structural node embeddings via diffusion wavelets[C]//ACM SIGKDD InternationalConference on Knowledge Discovery and Data Mining (SIGKDD’18). 2018.

[14] SUN Y, TAN W N, LI L X, et al. A new method to identify collaborative partners in social service provider networks[J]. Information Systems Frontiers, 2016, 18(3).

[15] CHEN H, CHUNG W, XU J J, et al. Crime data mining: a general framework and some examples[J]. Computer, 2004, 37(4): 50-56.

[16] 杨莉莉, 杨永川. 基于社会网络的犯罪组织关系挖掘[J].计算机工程, 2009, 35(15): 91-93.

YANG L L, YANG Y C. Crime organization relation mining based on social network[J]. Computer Engineering, 2009, 35(15): 91-93.

[17] 高建强, 谭剑, 崔永发. 一种基于通讯痕迹的社会网络团伙分析模型[J]. 计算机应用与软件, 2012, 29(3): 206-208.

GAO J Q, TAN J, CUI Y F. One social network clique analysis model based on communication trace[J]. Computer Applications and Software, 2012, 29(3): 206-208.

[18] 李万彪, 余志, 龚峻峰, 等. 基于关系数据模型的犯罪网络挖掘研究[J]. 中山大学学报（自然科学版）. 2014, 53(5): 1-7.

LI W B,YU Z, GONG J F, et al. An approach of crime network analysis based on association data model[J]. Acta Scientiarum Anturalium Universitatis Sunyatseni, 2014, 53(5): 1-7.

[19] 唐德权, 史伟奇, 凌志刚. 有组织犯罪集团挖掘算法[J]. 计算机系统应用, 2015, 24(9): 196-200.

TANG D Q, SHI W Q, LING Z G. Algorithm for mining organized crime[J]. Computer Systems & Applications, 2015, 24(9): 196-200.

Reasoning method for predicting crime partner by using intimacy network of bank accounts

LYU Fang, LU Haibo, WANG Wei, HUANG Junheng, WANG Bailing

(School of Computer Science and Technology, Harbin Institute of Technology, Weihai 264209, China)

In recent years, research on the law of capital transactions in the case of stakeholder-type illegal financial activities has attracted the attention of researchers. In order to solve the problem of using the bank transaction data to actively discover the abnormal account criminal crime partners, a crime partner prediction method based on the asymmetric intimacy network of the bank accounts was proposed. Firstly, a general network model for bank account transactions was established to embed time-series transaction data into the network structure. Then, using the direct and indirect transaction relationship information of the node, an account asymmetric intimacy calculation method was proposed. Finally, using the asymmetric interaction information of the nodes on the intimate network, the abnormal tendency index of the nodes is obtained. The experimental results on the actual data of the multi-level marketing group show that the crime partner prediction method based on the intimacy network can effectively find potential pyramid shelling members.

transaction network of bank accounts, intimacy network, direct intimacy, indirect intimacy, crime partner prediction

s:The National Key Research and Development Program of China (No.2018YFB2004201, No.2017YFB0801804), Frontier Science and Technology in Notation of China (No.2016QY05X1002-2),National Regional Innovation Center Science and Technology Special Project of China (No.2017QYCX14), Key Research and Development Program of Shandong Province (No.2017CXGC0706), the Fundamental Research Funds for the Central Universities (No.HIT.NSRIF.2020098), 2017 University Co-construction Project in Weihai City

TP391.4

A

10.11959/j.issn.2096−109x.2019062

吕芳（1990− ），女，山东阳谷人，哈尔滨工业大学（威海）博士生，主要研究方向为复杂网络、信息内容安全、数据掘。

陆海博（1998− ），男，甘肃酒泉人，主要研究方向为金融安全。

王巍（1975− ），女，黑龙江齐齐哈尔人，博士，哈尔滨工业大学（威海）讲师、硕士生导师，主要研究方向为金融安全、数据挖掘、自然语言处理。

黄俊恒（1966− ），男，河南新乡人，哈尔滨工业大学（威海）副教授，主要研究方向为数据挖掘、人工智能。

王佰玲（1978−），男，黑龙江哈尔滨人，哈尔滨工业大学（威海）教授、博士生导师，主要研究方向为信息对抗、信息安全、信息搜索、移动网络、金融安全。

2019−02−19；

2019−05−14

王佰玲，wbl@hit.edu.cn

国家重点研发计划基金资助项目（No.2018YFB2004201，No.2017YFB0801804）；国家前沿科技创新专项（No. 2016QY05X1002-2）；国家区域创新中心科技专项（No.2017QYCX14）；山东省重点研发计划基金资助项目（No.2017CXGC0706）；中央高校基本科研业务费专项资金资助 (No.HIT.NSRIF.2020098)；2017威海市大学共建基金资助项目

论文引用格式：吕芳, 陆海博, 王巍, 等. 基于银行账户亲密度网络推理的团伙预测研究[J]. 网络与信息安全学报, 2019, 5(6): 95-104.

LYU F, LU H B, WANG W, et al. Reasoning method for predicting crime partner by using intimacy network of bank accounts[J]. Chinese Journal of Network and Information Security, 2019, 5(6): 95-104.