基于支持向量机和动态样本的船舶有效功率预报

刘子祥，杨 磊，赵 峰

（中国船舶科学研究中心，江苏无锡 214028）

0 引言

快速性评估和预报是船舶设计的重要组成部分。在初步设计阶段，需要通过初步确定的船型主参数估算设计船型的阻力性能，以支持下一步设计工作的开展。此时，船舶线型尚未确定，所以无法进行模型试验或者数值模拟；而基于试验数据的预报方法可以利用初步确定的主参数进行预报，其预报精度一般也可以满足初步设计阶段的需求。

基于数据的预报方法多利用统计回归形成图谱、公式及方程等。在上个世纪，世界各大水池和相关研究机构推出了多种基于系列或非系列船型的估算方法，如泰勒系列、BSRA、S60、SSPA系列及Holtrop系列公式等。中国船舶科学研究中心于20世纪90年代至本世纪初在积累的大量试验数据的基础上建立了CSSRC系列快速性多元回归预报方法，并实现了程序化应用，该系列方法也是本文工作的重要参考。

这类方法得到了广泛应用，同时也存在一些固有的问题。首先，回归方法本身存在诸多问题和不便，而传统的样本分类处理方式也存在不合理之处。当前，对物理实验数据的利用有着信息化、知识化、自动化和智能化的趋势。对于传统方法存在的问题，可以引入属性细分的思想和数据挖掘的方法加以解决。本文尝试在一个拥有超过400艘（次）船型的数据库基础上，利用动态样本和支持向量机建立一种动态的有效功率预报方法。

1 支持向量机（SVM）简介

统计回归方法存在的问题主要有：回归公式的形式取决于研究者的经验，难有统一的标准，不便于比较；变量的选取受人为因素影响很大；在方法上，线性回归难以准确表述客观规律，信息丢失严重，而非线性回归难度太大[1]。这些问题可以通过采用机器学习算法加以解决，本文采用的是支持向量机回归方法。

支持向量机（support vector machine,SVM）由Corinna Cortes和Vapnik等于1995年提出，它在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势。它具有坚实的理论基础、简单明了的数学模型[2]。在机器学习中，SVM是与相关的学习算法有关的监督学习模型，像多层网络和径向基函数网络一样，可以分析数据、模式识别、用于分类和回归分析。

与传统统计学的大样本学习不同，SVM研究有限样本的学习规律。其引入奥卡姆剃刀原则，即用最简单的方法解决问题，寻找使经验风险最小的最简单函数，以获得学习器的良好泛化性能[3]。SVM的主要思想是建立一个分类超平面作为决策曲面，使正例与反例之间的隔离边缘最大化；SVM的理论基础是统计学习理论，是结构风险最小化的近似实现。

支持向量机有以下优点[4]：1）通用性，能够在分布广泛的各类数据集中构建函数；2）鲁棒性，不需要微调；3）有效性，在实际问题中总是最好的方法之一；4）理论完善，基于VC（Vapnik-Chervonenkis）推广性理论。

在“支持向量”x(i)和输入空间抽取的向量x之间的内积核这一概念是SVM学习算法的关键。其体系结构如图 1，其中K(x,xi)为核函数，其种类主要如下。

线性（linear）核函数：K(x,xi)=xTxi；

多项式（polynomial）核函数：

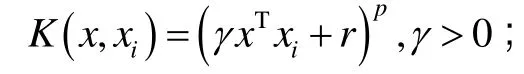
径向基（RBF）核函数：

图1 支持向量机的体系结构

针对不同的研究问题，SVM模型一般可分为2类：1）分类模型SVC（support vector classification）；2）回归模型SVR（support vector regression）。本文利用MATLAB的SVM工具箱建立回归模型，对船舶的有效功率进行预报。

2 数据库与动态样本

2.1 数据库的建立

中国船舶科学研究中心拥有国内规模最大的深水拖曳水池，多年来积累了大量快速性试验数据，并建立过一些性能数据库，笔者以此为基础进行了添加和整理。原计划参考CSSRC系列回归公式建立四参数和七参数模型，但在整理中发现数据中有部分参数记录不完整。为了充分利用数据，最终决定采用3参数和6参数的预报模型，对此分别整理建立了3参数和6参数的数据库，具体见表1。其中每个艘（次）为一艘船的一次实验记录；每个艘（次）中的每个有记录的傅氏数对应的功率为一个数据点。

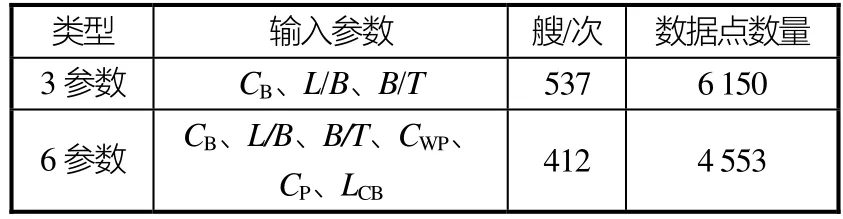
表1 数据库总体情况

数据库内各无量纲参数的范围如表2所示。

表2 全体样本无量纲参数范围

以上数据库中的船型均为单桨海船（包括少数江海联运货船），包括散货船、油船、集装箱船和少数客滚船，原始数据库中的双桨海船、内河船、高速船（艇）及多体船等特殊船型数据未引入。这些数据产生的年代涵盖1968年-----2017年，由于种种原因，较新的数据比较少，2007年之后的船型数据不超过50艘次。

2.2 动态样本方法

传统的回归方法一般将全体样本按照某一参数的范围进行分组后分别进行处理，如CSSRC系列多元回归预报方法。按照方形系数小于或大于0.78，将船型分为中等方形系数船和大方形系数船两类，然后分别给出不同的回归公式；Holtrop方法则是给出公式中一些可变参量的不同取值[5-6]。这类方法在实际操作中易于实现，但固定的分组也会带来问题。

首先，由于样本并非均匀分布，无论是采用回归方法或是学习型方法，得到的模型在理论上总是针对样本整体最优，而对某一样本点或细分区间并非最优，如图2和图3中所示的情况。

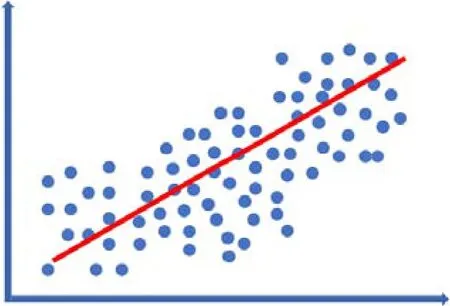
图2 全体样本回归情况

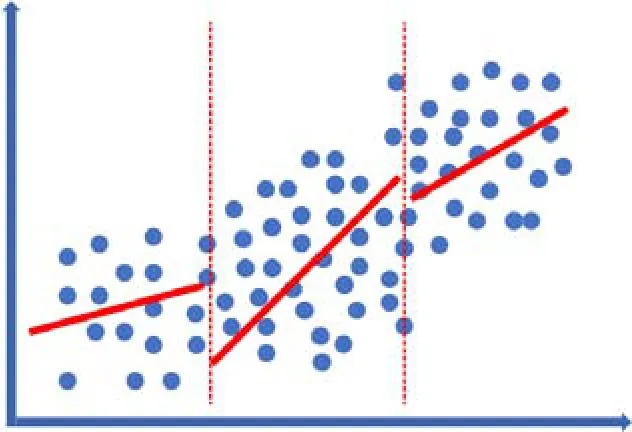
图3 分区域样本回归情况

其次，是根据某一参数特定值进行划分是否合理的问题。业内多采用CB=0.78作为划分标准，但CB略小于0.78设计航速却接近肥大型船以及CB大于0.78却有着较高设计航速的船型也不鲜见，采用这种分组方法时就显得十分尴尬。

对这类问题，应引入“属性细分”的思想，对数据进行精细化研究。在数据量比较丰富的情况下，有条件也有必要这样处理。属性细分不应只是简单地细化分组，这无法根本解决前述问题；而本文采用的动态样本方法，指的是根据预报对象的特征（主参数等），按照特定规则从全体数据中选出一组与预报对象相似的样本，以用于建立预报模型。这样一来，预报系统将针对每一条不同的船型建立单独的预报模型，而不再是建立某一参数区间内的泛用模型，这就实现了精确到每一个对象的精细化研究。

对于一般货船，无量纲船型参数中CB对阻力特征的影响最大，所以进行样本选择时，应首先考虑CB。以预报对象船型的CB为基准，给出一个较小的离散区间（如 0.83±0.002），在数据库中搜索CB满足这一区间的样本。如果搜得样本数量不满足最低限度，就按照一定步长加大离散区间再次搜索直到满足最低数量要求为止。样本选择过程大致如图4所示。

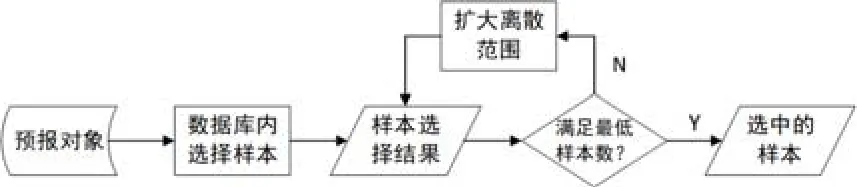
图4 样本选择流程

在选择过程结束后，得到的样本可以直接用于建模，也可以其他参数（如L/B或L3/∇）为标准进行第二轮选择。经过几个算例的测试对比，增加L/B为标准的二级选择确实可以进一步提高精度，但效果有限。下文中的测试算例均只以CB为标准进行了一级选择。

3 有效功率预测模型

本文在建模参数选择上参考了中国船舶科学研究中心的CSSRC系列回归公式，结合数据库内参数记录的实际情况，最终采用了3参数和6参数（均不包括傅氏数）2种模型，参数和样本数量的具体情况参见表1。

本文原计划采用常规的二因次或三因次换算方法[7]，即用预报模型预报剩余阻力CR或兴波阻力CW及形状因子1+k，最终换算到实船有效功率。实际操作中发现，数据库中1+k、CR及CW均有不同程度缺失，只有实船有效功率数据是完整的。鉴于此，本文仿照海军部系数定义了一个无量纲快速性系数PC。

式中：Δ为排水量，t；V为航速，kn；PE为有效功率，kW。可以看出其与海军部系数的区别在于将主机功率换成了有效功率，其余一致。预报模型给出预报对象各傅氏数对应的PC后，便可以根据其尺度换算出实船各航速对应的有效功率。整体的预报流程大致如图5所示。

图5 预报整体流程

4 算例与分析

4.1 算例基本情况

本文从数据库中随机抽取了25艘（次）样本作为测试算例。为了能够对3参数和6参数两种模型的预报效果进行比较，这25艘（次）算例均包含了完整的6个船型参数。在进行预报时，将测试对象从数据库中剔除。25艘（次）样本的基本情况见表3和表4。其中LCB为浮心纵向位置，单位为%LPP，舯前为正；其中有2个算例为同一艘船的不同载重状态，其余样本皆为不同船型，所有样本均无纵倾。

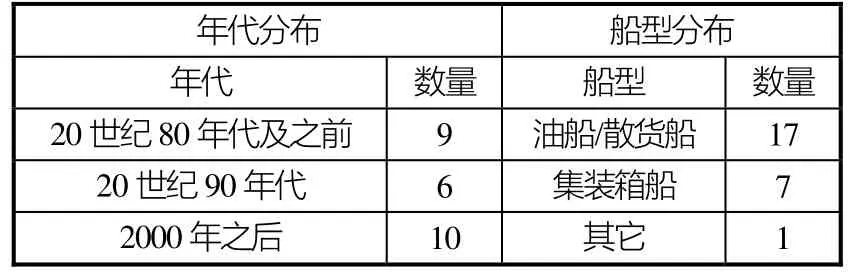
表3 算例基本信息

表4 算例无量纲参数范围

4.2 预报测试结果

首先将25艘（次）样本按照其全部原始航速记录点进行预报测试，共有305个数据点。其总体结果见表 5。通过对预报结果的观察可以发现，较大的误差值多出现在航速段的两端，即傅氏数较高与较低的时候，如图6～图9所示的样本5和样本12的预报结果和误差情况（均采用3参数法）。

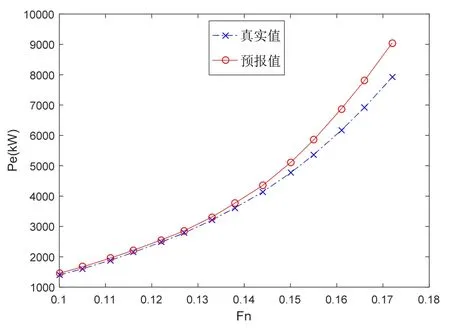
图6 样本5预报结果对比

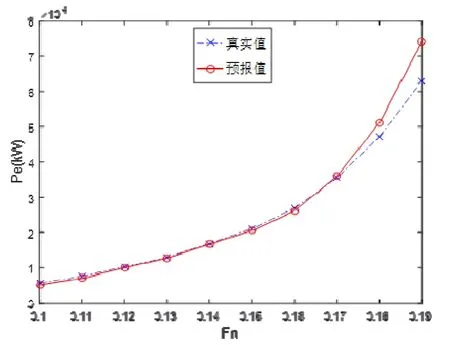
图7 样本12预报结果对比

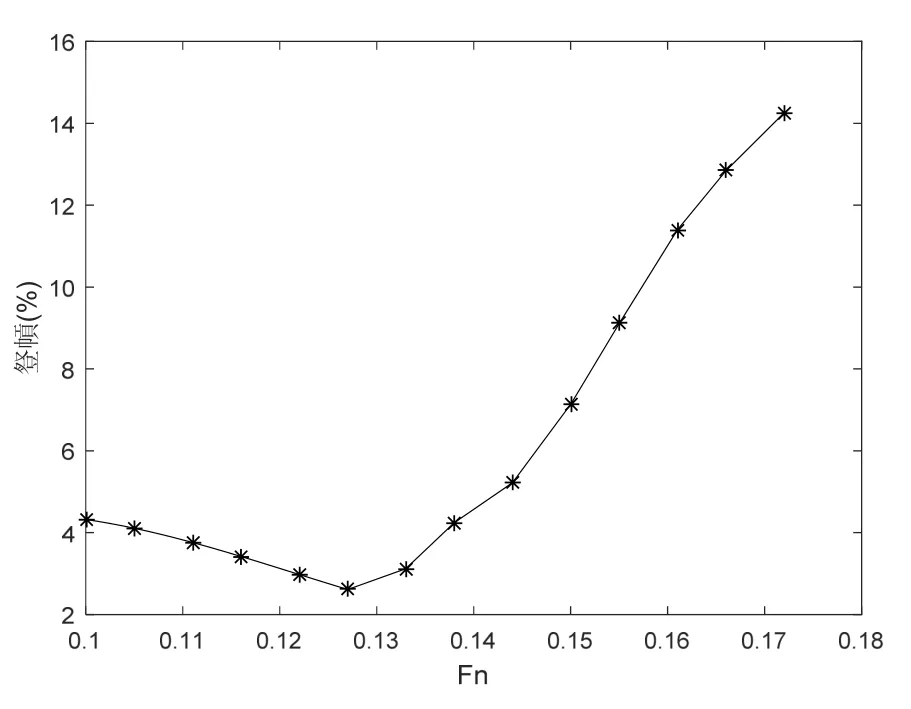
图8 样本5预报误差

图9 样本12预报误差

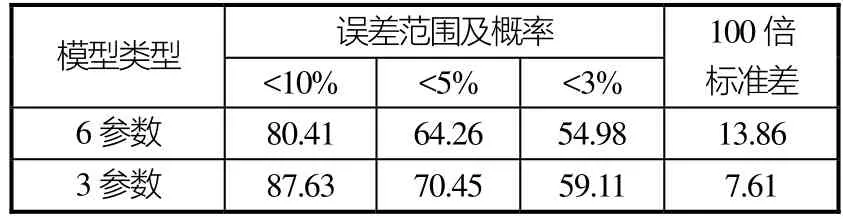
表5 原始航速数据点预报测试结果

出现这种误差分布特征的主要原因是航速偏高或过低时的数据相对较少，导致预报模型对这些部分的训练效果不如服务航速段；同时，这些情况下试验测量数据自身也难以保证精确。而服务航速附近的数据量充实，且实验测量结果也更准确。

考虑到实际应用，功率或阻力预报应该更多地针对服务航速区段。去掉一些偏离服务航速较远（即傅氏数偏高或偏低）的数据点后，剩余240个数据点的统计结果见表6。误差分布情况见图10和图11。

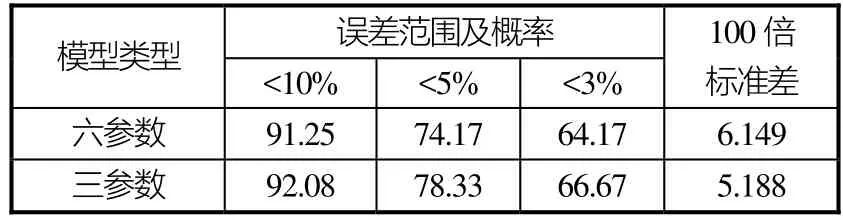
表6 服务航速段数据点预报测试结果

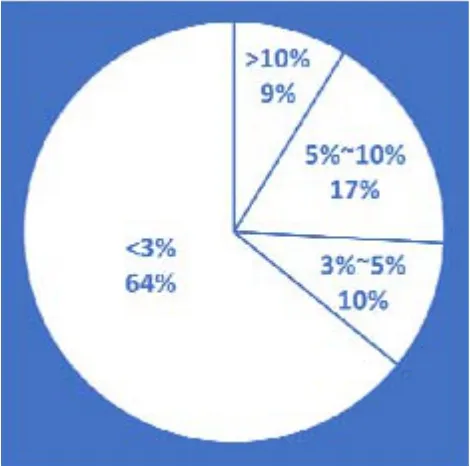
图10 六参数法误差分布情况

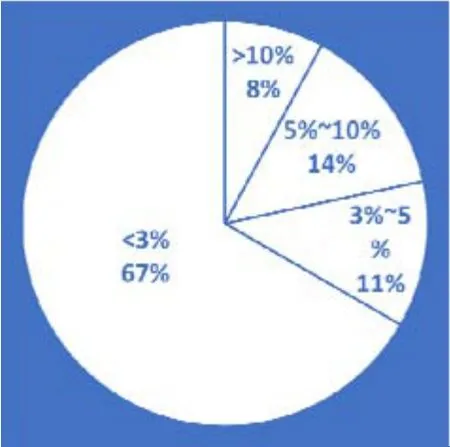
图11 三参数法误差分布情况

4.3 测试结果分析

造成预报误差的原因有很多，除了原始试验数据记录可能有误，以及数据库整理过程中可能出错外，主要有以下因素。一般来说，误差的产生都是多种因素共同作用的结果。

本文采用的无量纲系数PC，应用上与海军部系数相同，要求预报对象与样本的水下形状相近[8]。某些船型的水下形状可能相对比较独特，而其特点又无法在主参数上体现出来（尤其是本文未采用球首参数），在只采用主参数进行预报时可能会产生较大误差。

对于中低速船而言，船体摩擦阻力占了总阻力的大部分。在常规的预报和换算方法中，摩擦阻力系数由1957ITTC等固定公式求得，真正需要数学模型预报的只有剩余阻力或兴波阻力及船体形状因子。而本文因相关数据不完整，采用了整体预报方式，预报结果包括了全部阻力成分的影响，实际上放大了预报误差的影响范围。

某些船型可能有一个或几个主参数位于建模样本对应参数范围的边缘（图 12），或超出了这一范围，导致出现较大误差。例如CB太大，使系统选择建模样本时只能向CB更小的方向搜索，使建模样本CB范围整体严重偏移，将导致较大的预报误差。这一问题也是导致六参数法预报精度整体低于三参数法的原因之一，位于范围边缘或超出范围的参数成了干扰项，更多的输入参数会导致这种情况更多地出现。

本文所建立的数据库内数据年代整体偏早，近10年内的样本很少。随着船型设计的不断发展和优化，在主参数相同的情况下，新设计船型的阻力性能比起旧船型会有所变化，这也导致了算例中较新船型的预报误差整体大于旧船型。算例船型的预报误差与年代关系的大致规律可参考图13。

图12 参数范围边缘处的样本选择情况

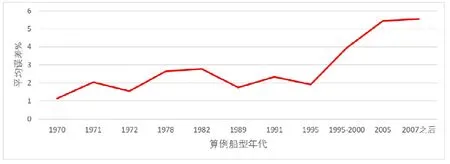
图13 算例误差与年代关系

5 结论

需要注意的是，本文中无论是数据库还是算例中的样本，大多是相互没有关系的各类船型（数据库包含有少数几个系列船型，数量很少）。这比采用系列船型更有实用价值，但也更加考验算法的泛化能力。显然，支持向量机的泛化能力是很不错的。就算例测试结果来看，本文提出的这套预报方法的效果还算令人满意。本方法可服务于初步设计阶段，对设计船型的有效功率进行快速近似预报，以支撑下一步设计工作的开展。

本方法仍有很大的改进空间。通过对误差产生原因的分析，可以在今后的工作中有针对性地加以改进。首先，在尽量补全缺失参数，尤其是形状因子1+k的基础上，改用常规的二因次或三因次换算方法，可以与本文中采用的PC系数换算法进行比较，以确定两者预报效果的差异；其次，增加参数范围判断功能，当预报对象的某参数超出建模样本对应参数范围时，给用户相应的提示；最后，尽可能继续扩充数据库，尤其是增加新船型样本，这将有力地提高本方法对新设计船型的预报精度。除此之外，还可以尝试采用神经网络等其他学习型算法来构建预报模型。