离散带轮带传动的受力分析

周宁，潘建州，储月刚，宋爱平

(扬州大学机械工程学院，江苏扬州 225127)

0 引言

带传动作为一种基本传动方式，具有结构简单、传递扭矩大、易于安装和维护等优点，在各机械领域得到广泛应用。但是目前普遍使用的带传动，其传动带轮是整体结构，使得整个带传动装置的传动比为定值。提出一种离散带轮传动机构，将固定的带轮离散成块，使机构的传动比可以变化。本文作者对离散带轮的受力情况进行分析，使用多楔带作为传动带，利用楔形增压原理提高机构传动的扭矩。

1 离散带轮传动机构

带传动是一种挠性传动，带传动具有结构简单、传动平稳和缓冲吸振等特点，在近代机械传动中被广泛使用。带传动的基本组成零件为带轮(又分为主动带轮和从动带轮)和传动带。传统的摩擦型带传动，从动带轮和主动带轮的基准直径为固定值，忽略微小的滑动率，带传动的传动比为主动带轮的基准直径与从动带轮的基准直径之比，在传动过程中为固定值。本文作者提出了一种新型的离散式变径带传动机构，将固定的皮带轮离散成若干个带轮块(为了便于表述，文中采用6个带轮块)，离散带轮块的内缩或者外扩实现了变径带轮理论直径的变小或者变大，从而实现传动比的改变，达到无级变速的目的，其结构如图1所示。

2 离散带轮块变径机构设计

离散带轮块的径向直径变化需要合适的结构来保证，由于金属带无级变速器和KRG无级变速器的结构特点，选择离散带轮块运动支撑部件为一对大小相同、布置方向相反的锥盘，每个带轮块与锥盘沿其母线方向滑动配合，利用一对大小相同、布置方向相反的锥盘(滚锥)在同一截面上的截面圆周不同来改变主、从动变径带轮传动半径的方法进行无级调速[1]。具体结构如图2所示。

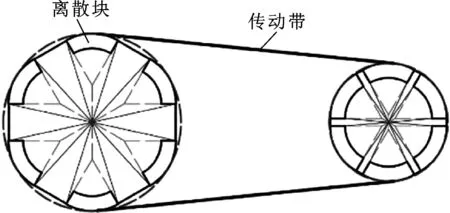
图1 离散式变径带轮的机构

图2 离散式带轮带传动模型

3 变径带轮与传动带的临界状态张力分析

目前普遍使用欧拉方程研究摩擦传动带拉力变化情况，欧拉公式具有参数少、计算量少的优点。假设在传动过程中，每一个带轮块与传动带的摩擦因数恒定，且传动带厚度远小于带轮块侧边相接触时的整圆直径。在变径带轮无级变速器处在临界打滑的状态下，选用欧拉方程分析传动带在离散式变径带轮上的张力关系[2]。

离散式变径带轮传动系统的传动比改变是依靠带轮块的径向移动来实现的，将整体式的皮带轮离散成带轮块，从而带与带轮的接触也是分段成块的。主动带轮的带轮块背离圆心移动，并以此状态传递动力和扭矩。如图3所示，传动带驱动主动变径带轮逆时针转动，在带轮块与传动带接触部分任意取一点C，连接O1C与O3C，O3C的长度等于带轮块圆弧半径r，O1C表示带轮块上的点C相对于旋转中心的实际半径R，其中带轮块不同位置上的实际半径R值也是不一样的。在点C处取一段圆弧带长ds，相对于带轮块圆弧中心O3对应的弧角为dα，同时相对于变径带轮中心O1所对应的弧角为dθ。设在点D的张力为T，在点C的张力为T+dT。N表示径向压力，周向摩擦力为fvN，fv表示传动带与变径带轮之间的当量摩擦因数。假设传动带的密度为ρ，横截面积为A，该传动系统在角速度为ω1时高速平稳运转。

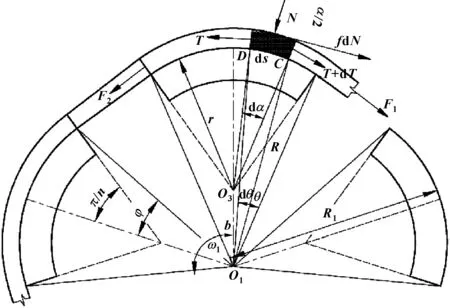
图3 变径带轮的张力分析

对带轮径向方向进行受力分析，则带轮的支撑反力为

(1)

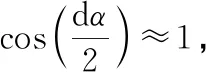
N=Tdα

(2)

传动带在圆周方向上的力为

(3)

(4)

由于ds≪1，近似认为Rdθ≈rdα，因此有：

(5)

式(5)代入式(2)和式(4)得：

(6)

fv·N=dT

(7)

将式(7)代入式(6)得：

(8)

积分后得：

(9)

式中：C为积分常数。由边界条件θ=0时T=F1，可得

T=F1efvθ

(10)

由于θ=2φ时，T=F2，因此有：

(11)

公式(11)给出的是在单个带轮块在相对于变径带轮中心O1的整个包角得到的力F1和F2。实际情况下，在传动带和变径带轮接触传动中，传动带与变径带轮块的接触个数不止1个。

如图4所示，传动带相对于变径带轮包角的大小决定了所包含的变径带轮块的个数，传统的带轮包角计算已经趋于成熟，本文作者直接引用已有的计算公式[3]：

(12)

式中：α1表示在离散带轮传动系统中变径带轮始终较小的带轮包角；α2表示在离散带轮传动系统中变径带轮始终较大的带轮包角；dd1和dd2分别表示较小带轮和较大带轮的理论直径；a表示主、从动变径带轮的中心距。

图4 带轮总包角

公式(12)计算出来的变径带轮的理论带轮包角αi(i=1或2)是由K个完整的周期角σ和一个部分带轮块的包角σ′组成。因此αwi可以写成：

αwi=K·σ+σ′

(13)

在此，变径带轮的有效包角被定义为：在带轮包角αwi中，传动带与带轮块实际接触的包角为变径带轮块的有效包角，采用α′wi表示带轮的有效包角，因此可以得到：

α′wi=k·2φ+σ′

(14)

式中：2φ表示单个带轮块相对于旋转中心O1的整个包角。

变径带轮的有效包角α′wi的取值有两种情况：

(1)如果(k-1)σ+2φ≤αwi

(2)如果kσ≤αwi

因此，变径带轮在有效包角下的临界摩擦力计算公式如下：

和

(15)

假设在传动过程中传动带的总长度是保持不变的，并且假设传动带是线性体，可得：

Fk+2+F1=2F0

(16)

式中：F0表示传动带的初张力。

传动带与变径带轮的临界摩擦力Fec可以表示为

(17)

计算结果表明：提出的离散式变径带轮传动系统基于传统的带传统，其受力情况符合常规。通过将传统的一体式皮带轮离散成带轮块可以实现带传动系统传动比的连续变化，实现无级变速。

4 采用多楔带实现大扭矩传动

带的预紧力反映带的松弛程度，它对带的传动能力、寿命和压轴力都有明显的影响。预紧力不足，导致总摩擦力下降，容易打滑，效率降低；预紧力过大，对支撑轴以及轴承的径向作用力大，加速磨损，降低寿命。因此，保证适当的预紧力是保证带传动的重要基础。在一定范围内，F0越大，带与带轮间的正压力越大，则传动时的摩擦力越大。为了使文中提出的离散式变径皮带轮传动系统实现大扭矩无级变速传动，传动带采用多楔带，实物如图5(a)所示。多楔带兼有平带柔顺性好和V带摩擦力大的优点，广泛应用于传递功率大和要求结构紧凑的场合[4]，其受力分析如图5(b)所示。

图5 多楔带实物及受力分析

多楔带的楔角为40°，假设多楔带楔形两侧的受力情况相同，即左右两边正压力均为N，Fe为有效拉力。

对多楔带竖直方向进行受力分析得：

2Nsin20°=Fe

(18)

(19)

由sin20°≈0.342，得N=1.46Fe，可以提供的周向摩擦力N为2.92fvFe，大约是同预紧力条件下，平带周向摩擦力的3倍。因为带传动所传递的功率P与有效拉力成正比关系，且带传动的有效拉力等于传动带工作表面上的总摩擦力，所以多楔带可以极大地提高传递功率，与离散带轮块组合可以实现大扭矩无级变速。

5 总结

文中分析了离散式变径皮带轮带传动系统的主要传动部件：变径带轮，对变径带轮的结构做了具体的受力分析，比较了变径带轮与普通带轮的主要不同点；结合普通带轮传动计算临界摩擦力的理论，推导出了离散变径带轮的临界摩擦力计算公式。结果表明：离散式变径带轮具有大扭矩无级变速的能力。

(1)将一体式带轮设计为组合式离散带轮，从而实现带轮直径的变化。

(2)分析了离散带轮上传动带临界状态的张力，推导出离散变径带轮传动机构的临界摩擦力计算公式。

(3)离散变径带轮传动机构为新型无级变速器的实现提供了基础，该新型无级变速器具有传动扭矩大、结构紧凑、缓冲吸振、不需润滑等优点。