基于GIS和随机森林模型的泥石流敏感性分析——以吉林省洮南市北部山区为例

扈秀宇，秦胜伍，窦 强，刘 飞，乔双双，董 冬

（1.吉林大学 建设工程学院，吉林 长春130000；2.吉林省地质环境监测总站，吉林 长春130000）

泥石流是由土、碎石及水组成并在重力作用下以＞10 m／s速度［1］前行的混合物，是山区最具破坏性的自然灾害之一。泥石流令其物源区水土流失，流通区的沟谷遭受侵蚀；其在堆积区淹没住房、农田和林地，堵塞河流。研究区洮南北部山区于2014年夏季由于持续性强降雨，形成126处泥石流灾害，使人民财产安全受到威胁。为减少泥石流灾害所带来的损失，利用影响泥石流发育的因子及已发生的泥石流灾害点进行训练建模，从而能够对泥石流敏感性分级评价，评价结果能够有效而直观地预测泥石流敏感区域。

对于泥石流敏感性研究，国外起步较早。1976年，联合国委托国际工程地质联合会开展泥石流敏感性研究，此后逐渐成为泥石流地质灾害防治评价的重要内容。20世纪80年代初，美国学者Kovacs等利用定性评价方法对泥石流敏感性建立了评价模型，为泥石流敏感性评价提供了新的方向［2］。此后利用因子叠加评估地质灾害危险度的方法被很多学者使用。而国内起步稍晚，1986年，谭炳炎［3］第一次对泥石流的易发性进行了数量化综合评价。1988 年，刘希林［4］首次使用多因子叠加方法对泥石流危险性进行研究。1994年，唐川等［5］利用数值模拟对泥石流堆积扇进行了危险度评价。之后，众多学者利用定性和定量分析方法对泥石流进行敏感性分析，如层次分析法［6］，模糊 数 学 法［7-8］，信 息 量 法［9］，回 归 分 析［10］，频率比法［11］，人工神经网络［12］等。这些方法由定性到半定量再到定量过渡并且已应用较长时间，使用范围广泛。但不能对因子进行权重分析，而且在灾害点和评价因子较多的情况下，上述方法并不能在运算复杂大数据上取得优势。而现在兴起的人工智能算法对大数据能够进行高速处理并进行自组织学习。

随机森林算法是以简单高效著称的人工智能算法［13］，开始是在2001年由Breiman提出的一种人工智能算法［14］，用于市场营销、医学领域，预测客户的保留与流失以及预测疾病风险与病患的易感性［15］。它将决策树作为单元进行集成学习的树形分类器组合算法。其相比于决策树及其他算法，它集成了Bagging算法和随机选择特征分裂特点，准确率较高，能够处理大数据并评估每个因子在分类上的重要性。本文在研究区使用随机森林进行泥石流敏感性建模，然后与概率统计方法中使用广泛且简单高效的频率比法进行比较验证。以期能够客观验证随机森林模型的效果，又能对洮南北部山区泥石流灾害预警提供直观有效的参考。

1 研究区概况

研究区域位于吉林省洮南市北部，其面积约1 181 km2。洮南地处东三省与内蒙古交界中心。地理坐 标 为 东 经122°45′—122°48′，北 纬45°19′—45°21′。洮南市总体上属北温带大陆性季风气候区，春季干燥多风，夏季温热多雨，秋季凉爽多旱，冬季寒冷少雪，平均年降雨量391.3 mm。洮南地处大兴安岭东麓，松嫩平原西部，北部丘陵高低起伏，嫩江支流发源于此。研究区多属于低山丘陵，低山海拔多在500～550 m，坡度多在25°以下，主要由花岗闪长岩、凝灰质砂岩和花岗岩等组成。丘陵海拔250～500 m，相对高度在百米以下，以低丘陵为主。多由火山碎屑岩、花岗岩等组成。山坡残积，坡积物发育。研究区泥石流频发，大部分位于洮南市西北角，包括胡力吐乡、万宝乡及部分万宝镇、东升乡、那金镇。泥石流多发生在低山丘陵区，山峰呈北东～南西方向展布，山坡坡度为15°～25°，坡面冲沟发育，植被覆盖率较低，出露岩石主要是侏罗系碎屑岩和燕山期岩浆岩。发生泥石流的坡面由于过度开垦、放牧，植被覆盖率低，裸露岩石极易受到风化，坡面抗冲刷能力较差，致使泥石流多沿河流发育，多威胁农田，屋舍和道路。

研究区经调查发现126处泥石流灾害，对此126处灾害点随机分为训练集灾害点和验证集灾害点。训练集灾害点用于数据的训练和模型的建立；验证集灾害点用于验证模型的可靠程度。运用随机森林算法进行数据分析时，传统方法是将数据按照7∶3进行训练集和验证集的划分。所以本文将训练集灾害点划分为85个（70%）和验证集41个（30%）用于模型建立和验证。

2 研究方法

2.1 评价因子选取

影响泥石流发育的因子十分复杂，因子之间相互联系，相互影响，本文泥石流评价因子主要依据研究区泥石流灾害的分布及发育现状，在充分考虑研究区资料获取难易程度以及研究尺度后，选取地表高程、坡向、坡度、平面曲率、剖面曲率、到河流距离、土地利用、岩性、归一化差分植被指数（NDVI）及地形湿度指数（TWI）作为评价因子，利用ArcGIS进行分类后如图1及附图1所示。数字高程数据（DEM）直接反映研究区的地形起伏变化，在一定程度上反映了沟谷，植被变化及堆积物的状态。DEM 栅格大小为30 m×30 m，高程范围为163～650 m，将其按照自然断点法分为5 类，分别为＜250，250～300，300～350，350～410，410～650 m。

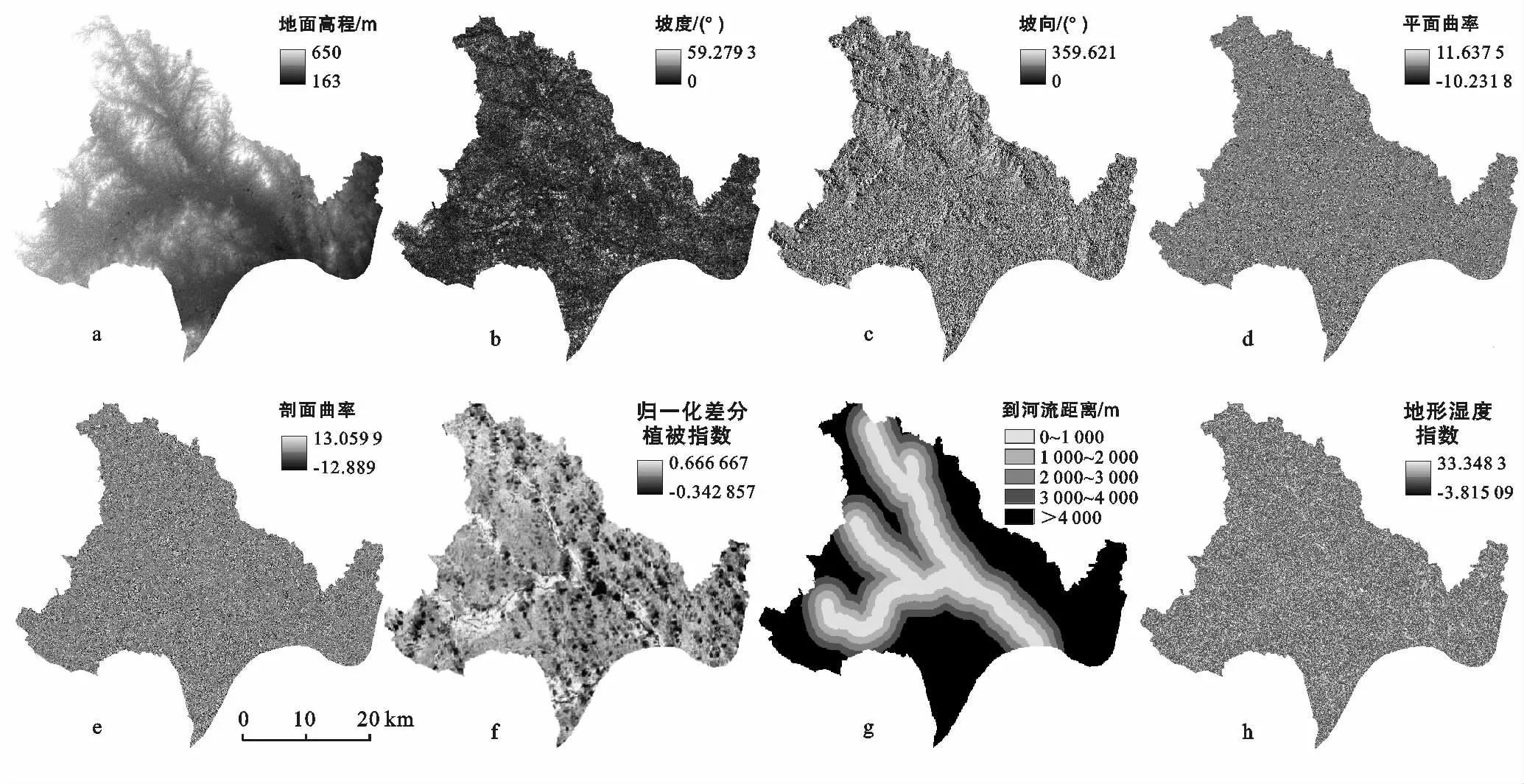
图1 泥石流敏感性分析的评价因子

坡向对泥石流发育主要影响山坡岩体风化程度以及植被生长发育情况。ArcGIS计算坡向是按照每个栅格与相邻栅格值变化最大的下坡方向计算，故会产生－1°坡向，即不具有下坡方向的平坦区域。研究区坡向分类按照自然间断点分为10类，分别为－1°，0°～22.5°，22.5°～67.5°，67.5°～112.5°，112.5°～157.5°，157.5°～202.5°，202.5°～247.5°，247.5°～292.5°，292.5°～337.5°，337.5°～360°。

坡度对于泥石流的发育是十分重要的一个因素，常被直接用作泥石流敏感性制图。研究区坡度变化范围为0°～59.28°，其分为6类，分别为0°～4°，4°～7°，7°～11°，11°～16°，16°～24°，24°～59.28°。

平面曲率及剖面曲率代表地形表面的凹凸程度，其间接影响泥石流发育范围。平面曲率值为正值时，表明地形表面为向上凸，负值表明地形向下凹，值为0时，表面为水平。剖面曲率与平面曲率相反，正值表明地面向下凹，负值表明向上凸。平面曲率划分为5类，分别为－10.23～－1.14，－1.14～－0.28，－0.28～0.32，0.32～1.17，1.17～11.64。剖面曲率划分为5类，分别为－12.89～－1.39，－1.39～－0.47，－0.47～0.24，0.24～1.15，1.15～13.06。

泥石流常发生于山区沟壑，经常堵塞河流，而河流沟谷也为泥石流提供流动通道，使其流通距离加长，规模变大。本文在ArcGIS平台上对河流进行缓冲区划分，分为5个缓冲区，分别为0～1 000，1 000～2 000，2 000～3 000，3 000～4 000，＞4 000 m。

地形湿度指数（TWI）表征地形与土壤随空间的水分分布，是一种对径流长度及产流面积的定量描述［16］。其直接反映了土壤含水量随地形及空间变化规律，以及间接反映研究区的水土流失状况。研究区地形湿度指数分为5类，分别为＜3，3～6，6～9，9～12，12～33.2。

归一化差分植被指数（NDVI）通常与植物蒸腾作用、光合作用有关，是指示植被生长状态及植被覆盖度的最佳指示因子［17］。其优点是可以消除太阳高度角、卫星观测角、地形、云影及大气相关的辐射影响。其计算公式为：

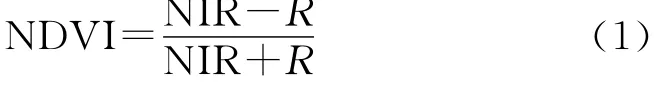
式中：NIR——近红外波段；R——红波段处的反射率值。NDVI取值在－1与1之间，负值表示地面覆盖为对可见光高反射的物体，如云、水、冰、雪等，0表示近红外波段与红波段近似，代表裸地或岩石。正值代表植被覆盖，其值越大，植被覆盖度越大。研究区NDVI范围－0.34～0.67，分为5 类，分别为－0.34～0，0～0.22，0.22～0.32，0.32～0.43，0.43～0.67。

土地利用则分为采矿用地、城市建设用地、道路、湿地、农林用地及河流湖泊。岩性分为火山碎屑岩、凝灰质砂岩、花岗岩、砂岩、全新世沉积物及更新世沉积物。

评价因子数据来源如表1所示。

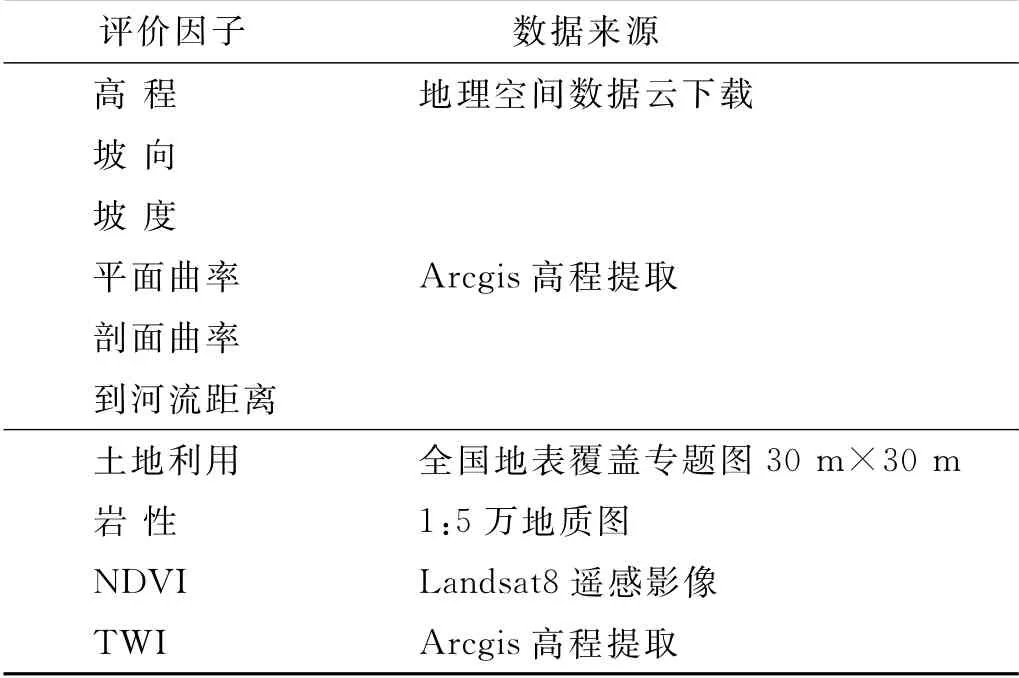
表1 评价因子数据来源

2.2 随机森林模型

随机森林由很多决策树模型组成的分类模型。它与Bagging算法相同，计算过程如图2 所示：①采用Bootstrap方法随机放回地选择i个训练数据集中的数据D1，D2，D3，…，Di；②构造i个决策树进行分类训练，得到i个弱分类器C1，C2，C3，…，Ci。③对得到的弱分类器按照投票组合成强分类器。由于组成随机森林算法（RF）的决策树模型不进行剪枝，可得到偏差较小的分类树，确保RF 对测试数据分类训练的准确性。弱分类器之间能够互补差异，把单个分类器的误差降到最小，从而增强整体的准确率。

与其他算法相比，随机森林算法还可以对分类特征（即评价因子）进行重要性分析，得出每个评价因子的重要性。计算重要性的方法为重要性评分（VIM），其主要分为两种计算方法，分别为基尼指数计算和OOB误差率置换计算法。本文的模型使用基尼指数计算节点的不纯度来衡量特征的重要性，计算过程如下。

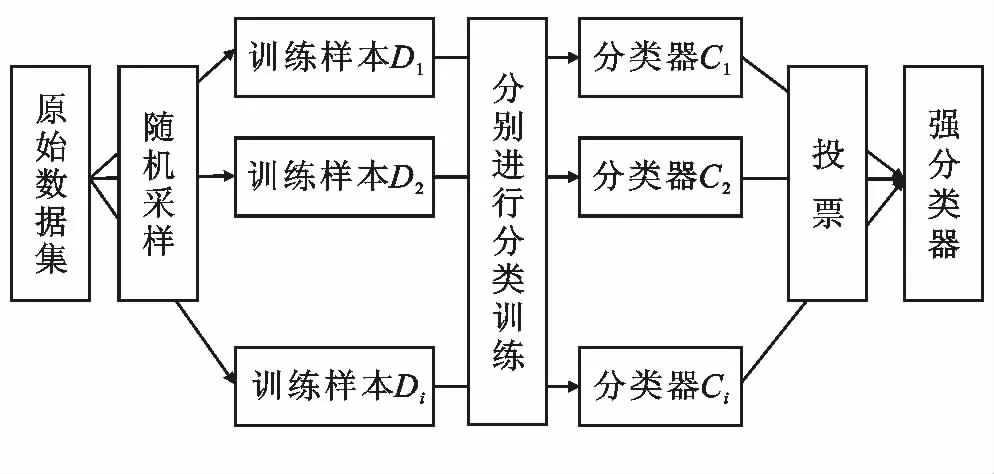
图2 随机森林方法流程

假设有M 个特征为X1，X2，…，Xm，基尼指数计算公式为：

式中：K——K 个类别；Pck——c节点中类别k 所占的比例。

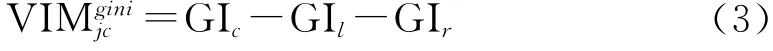
式中：VIMjc——第j个因子在节点c 的重要性；GIl，GIr——向下分枝后两个新节点处的基尼值。

式中：VIMij——第j个因子在第i个树的重要性。

假设有n 个决策树，则第j 个因子的重要性为VIMj。

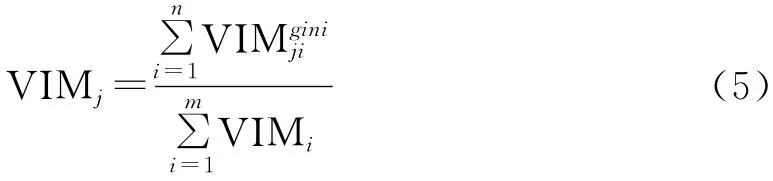
根据随机森林算法原理，结合GIS进行随机森林评价的过程为［18-20］：

（1）对泥石流灾害点数进行分类，70%（85个）灾害点作为训练集进行随机森林训练计算，其余30%（41个）作为验证数据集对结果进行预测率验证。

（2）根据研究区泥石流发育特点，选取10 个评价因子。

（3）从训练数据N 中使用Bootstrap 重抽样方法随机有放回地选出K 个不同的样本，进行n 次采样，得到n个训练集。

（4）对n个训练集，分别训练n个决策树模型。

（5）对于单个决策树模型，假设训练样本特征的个数为M，那么每次分裂时都从M 中抽取m 个特征作为当前节点的分裂特征集。

（6）每棵树都一直这样分裂下去，直到该节点的所有训练样例都属于同一类。在决策树的分裂过程中不需要剪枝。

（7）利用生成的各个决策树组成随机森林，其预测结果取K 棵决策树的平均值，从而得到最终预测结果。

（8）根据模型预测结果进行敏感性分级，利用GIS生成研究区泥石流敏感性评价图，并得到评价因子重要性评估值。

2.3 频率比模型

利用概率统计的方法，对10个评价因子进行频率比方法的统计计算，然后对评价因子进行叠加，得到泥石流敏感性评价图。首先利用随机森林划分的训练集（70%）与验证集（30%）对灾害点分类。其次对每个泥石流评价因子的FR 计算。利用ArcGIS将泥石流训练集灾害点与每个评价因子图叠加提取所需数据，并且使用公式（6）计算每个类别的频率比值。这一步对每个评价因子进行计算（如表2所示）。最后，通过将常规FR 方法中的FR 值（式7）求和来创建泥石流敏感性指数并进行敏感性制图。

式中：Nij——因子i的第j 个子类中的泥石流灾害点数；Aij——相应子类所占栅格数；NT——泥石流灾害点总数；AT——调查区域所占总栅格数。

式中：DSI——泥石流敏感性指数，敏感性指数越大，泥石流发生的概率越大；FR——每个因子级别的计算频率比；N——因子的数量。

3 结果及分析

3.1 模型结果

随机森林算法模型（RF）通过SPSS Modeler 18.0软件构建，参数设置为500个决策树，节点个数m 为评价因子个数（10 个）的平方根，故将m 取值为3。样本数据使用训练集进行训练，使用自然断点法对滑坡敏感性图进行分类，共分为5个敏感区，分别为极低敏感区、低敏感区、中敏感区、高敏感区和极高敏感区，最后得到敏感性结果见附图2，由附图2可知，大约有14.6%区域对泥石流敏感性极低，其余22.2%，30.3%，17.6%，15.3%的区域分别表现为低、中、高和极高敏感性。位于极低、低、中、高、极高敏感性区的训练集灾害点分别有2，5，8，30个及40个，位于高敏感性区以上的灾害点占82.3%。

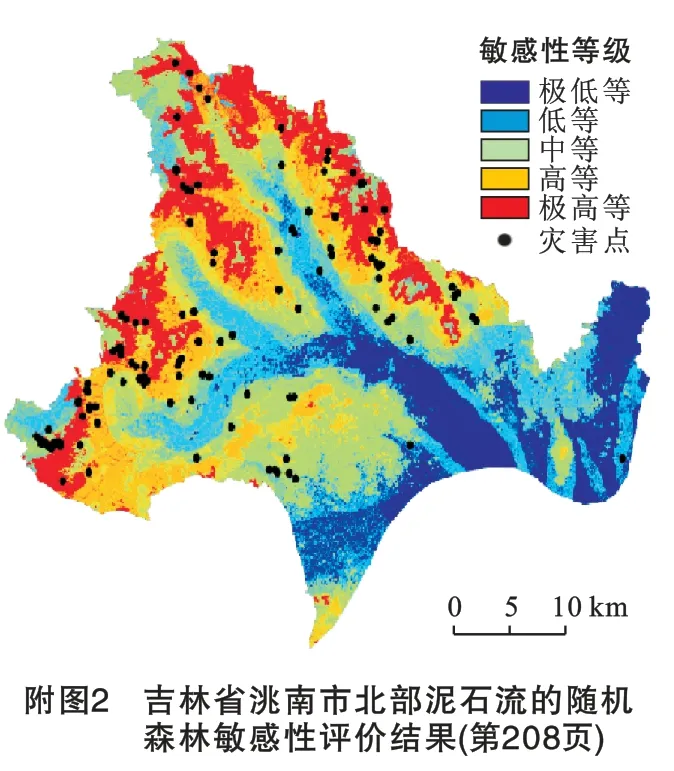
随机森林算法模型模拟出的高敏感和极高敏感区主要集中在洮南市那金镇东北部地区，胡力吐蒙古族乡北部地区，万宝乡大部分地区和万宝镇西部和北部地区。高敏感区共分布已发生泥石流61处，占训练集的71%。高程大部分位于250 m 至400 m，坡度分布为10°至30°，此段区域主要为低山至河流过渡区域，高差较大，坡度适中，能够为泥石流提供势能，同时并不影响农业开垦；NDVI分布为0至0.3，地表主要为裸地和农作物，土地类型中农业用地占90.4%，致使水土保持能力变差，土壤疏松，岩性主要为易风化的火山碎屑岩和凝灰质砂岩，为泥石流形成提供充足的物质来源；高敏感区地表沟谷发育，泥石流灾害点距河流距离分布大多大于3 000 m，泥石流发育多沿沟谷流通，而沟谷前的平原地区又为泥石流提供堆积场所，致使大型河流对研究区的影响较低。

随机森林算法模型根据决策树各个节点的平均基尼值的减少量来计算评价因子的重要性，并对所计算的因子权重进行归一化处理。如图3所示，坡度、高程、TWI和坡向是影响研究区泥石流发育十分重要的4 个因子，重要性均超过10%，占全部因子的52.57%。平面曲率、到河流距离、剖面曲率和NDVI，重要性占比为37.24%，对泥石流发育的影响较为重要。岩性和土地利用重要性占比为10.2%，对泥石流发育影响较轻。

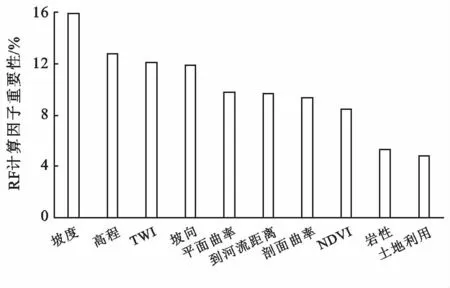
图3 吉林省洮南地区随机森林评价因子重要性

频率比敏感性评价中，按照公式（2）计算10个评价因子频率比模型，然后根据公式（3）在ArcGIS 中进行叠加计算，由此得出泥石流频率比敏感性图，如附图3所示。按照自然断点法对其进行分类，与随机森林模型相同，共分为5 个敏感区，极低敏感区12.4%，低敏感区占19.1%，中敏感区占23.7%，高敏感区占26.9%，极高敏感区占17.9%。其中训练集中位于极低、低、中、高极高敏感区的灾害点分别有0，10，16，27，32个，位于高敏感性区域以上灾害点占训练集的69%。

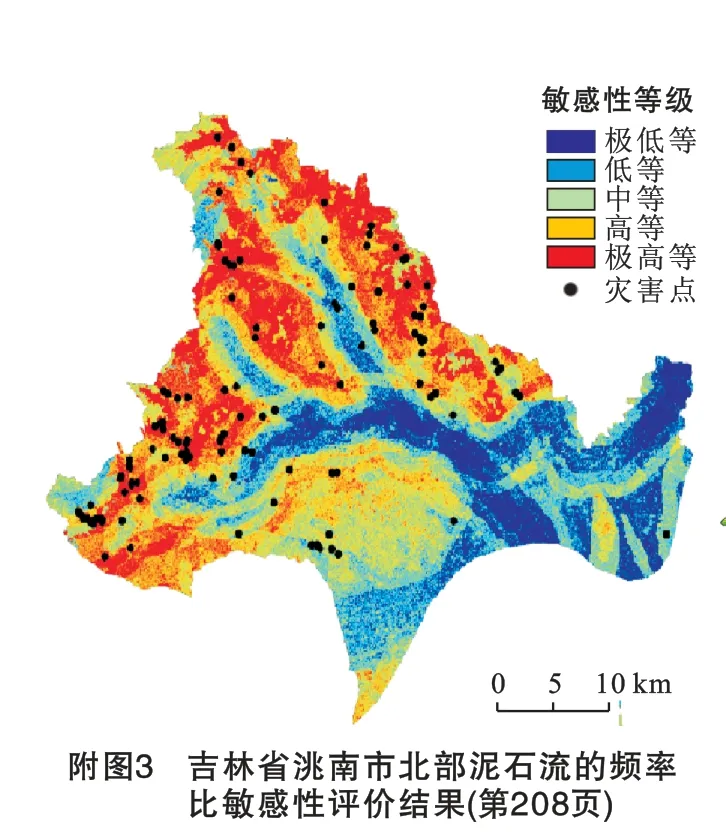
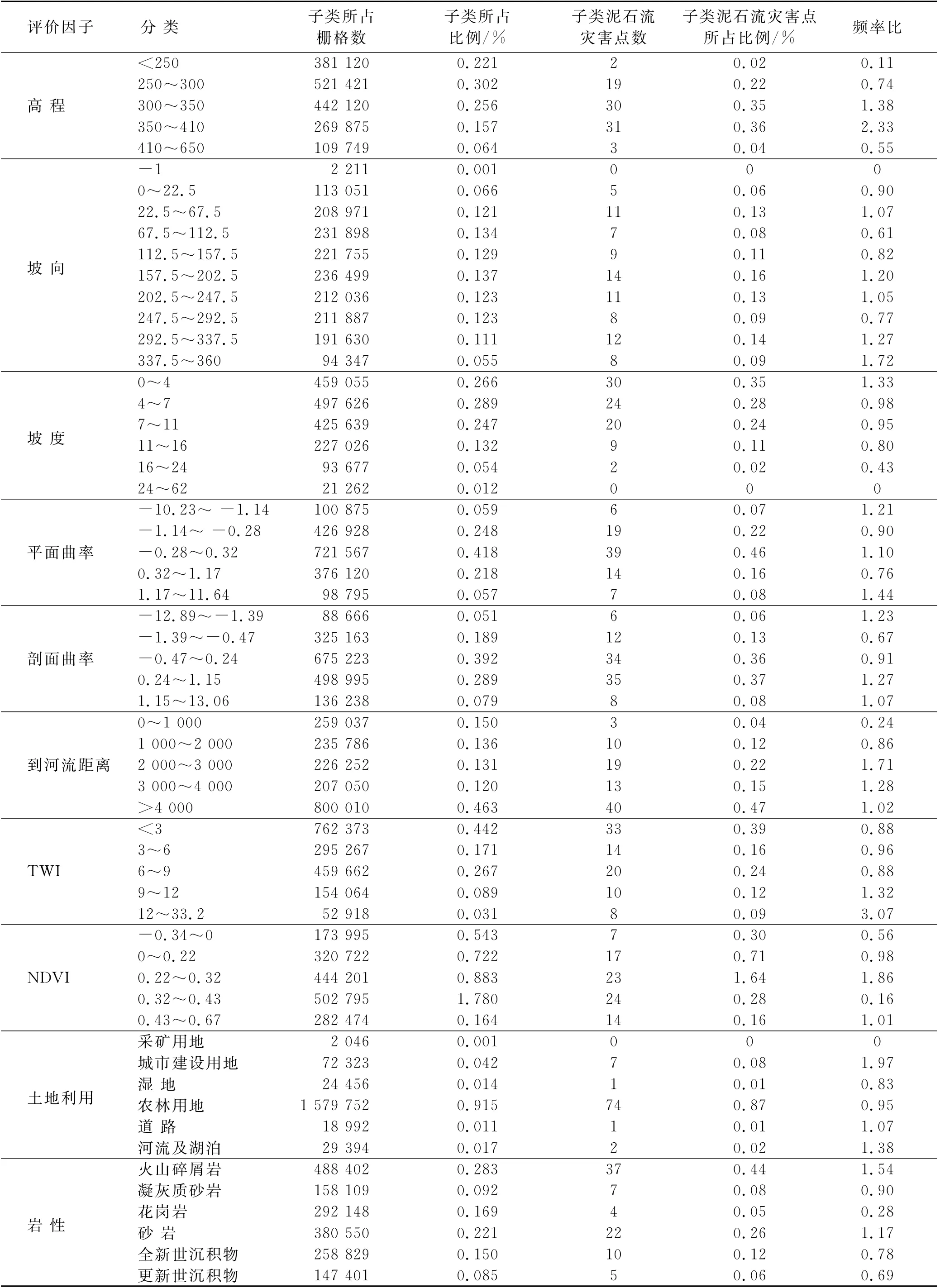
表2 泥石流敏感性频率比值

3.2 ROC曲线验证

ROC曲线即称受试者特征曲线（receiver operating characteristic curve），其可以广泛应用于医学检验及疾病预测［21-22］。每个灾害点及其评价因子组成的个体相当于医学检验中的受试者，再将发生泥石流及未发生泥石流作为二分类（正类及负类）进行分析，得到每个模型所对应的ROC 曲线及其曲线下面积（AUC）［23］。AUC 是判断所用随机森林及频率比模型的优劣标准，当AUC＝0.5时，说明其模型结果不具有参考价值，而小于0.5则说明模型不符合真实情况。AUC大于0.5时，其值越靠近1，说明模型效果越准确。

由于将样本灾害点分为训练集及验证集，所以利用训练集数据可以得到模型准确率ROC 曲线，其曲线下面积即模型的准确率。验证集数据得到预测率ROC曲线，用于验证模型是否预测准确，其曲线下面积为预测率。随机森林及频率比模型准确率及预测率如表3所示。

表3 模型准确率及预测率结果

随机森林与频率比的准确率为88.4%与86.4%，说明随机森林模型训练效果较频率比结果准确。而预测率两者相差较大，随机森林预测率达到90.4%，其模型预测结果准确性高。频率比预测率为75.1%，和随机森林模型相比有一定差距，模型预测效果一般。准确率和预测率之间的差值可以提现模型的稳定性，随机森林准确率和预测率相差2%，而频率比相差11.3%，由此可知随机森林模型更稳定可靠。

4 结论

吉林省洮南市北部山区是泥石流多发区域，根据该地区的地形因素、地质因素、植被因素及人为因素，选择了10个评价因子及随机森林模型进行泥石流敏感性评价，并用频率比模型与其对比验证。得到以下结论：

（1）随机森林算法应用于泥石流敏感性分析无需提前设置因子权重，计算过程简化，运行平台丰富，可在可视化软件SPSS Modeler上运行，使用简便。

（2）随机森林模型可以对评价因子进行重要性分析，便于分析各评价因子对泥石流发育的影响。

（3）随机森林模型结果将研究区域划分为5个泥石流敏感性区域，分别为极低、低、中、高和极高敏感区，分别占研究区的面积的14.6%，22.2%，30.3%，17.6%，15.3%。位于各分区的泥石流灾害数占比为2.35%，5.88%，9.41%，35.29%和47.06%。泥石流发生数随敏感性等级增大而增大，敏感性分级符合实际野外调查结果。

（4）随机森林方法的准确率与预测率分别为比频率比方法高，准确率与预测率相差较小，模型稳定。随机森林模型可以应用于研究区的泥石流敏感性分析且效果良好。