基于自适应变异方法的差分进化算法
刘勇 于颖锐 李满仓 张斌 王冬勇 王星博

摘 要:在工程实际应用中,常需对高维复杂的优化问题进行求解。差分进化算法是目前智能优化算法中性能最优的算法之一,可在很多工程问题中得到应用。传统的差分进化算法存在收敛速度慢、易陷入局部最优解等问题。本文对差分进化算法的变异方法进行研究,提出一种根据种群进化代数自适应的变异方法。数值结果显示,本文提出的自适应变异方法可有效避免种群早熟和局部最优解的问题。
关键词:优化算法 差分进化算法 自适应
中图分类号:O224 文献标识码:A 文章编号:1674-098X(2019)07(c)-0136-03
在科学、工程、经济、前言研究等领域,对很多科学分析、系统控制、经济模型、人工智能等问题都需要进行优化问题的求解。求最优化问题的方法称为最优化方法,传统的最优化方法包括单纯形法、最速下降法、共轭梯度法等,具有计算效率高、可靠性强、理论比较成熟等优点,但是通常要求待求解问题有精确的数学模型,对问题的依赖较强,并且大多不具备全局最优化的特点。而工程实际问题中,常遇到高维度、非线性、多峰值,甚至目标函数不连续、不可微的问题,传统方法求解困难。20世纪80年代以来,以模拟退火算法、遗传算法等算法为代表的智能优化算法得到广泛的研究和应用,其中差分进化算法以其特有的有点,成为最优异的智能优化算法之一[1-2]。
差分进化算法是根据父代个体间的差分矢量进行变异、交叉和选择操作,与其他进化算法一样容易限入局部最优,存在早熟收敛现象。本文从其算法中变异的本质出发,提出一种根据种群进化代数自适应变化的变异因子,其作用是:在种群进化前期,种群变异主要通过随机父代进行扰动,种群多样性高,全局搜索能力越强;在进化后期,种群变异集中在优秀个体附近,提高收敛速度。
1 差分进化算法及自适应变异方法研究
1.1 差分进化算法及其影响因素分析
在差分进化算法中,一般称维度与目标函数决策变量数相同的单个向量为个体,由NP个个体构成的集合称为种群,NP称为种群规模。差分进化算法在算法执行过程中,保持种群规模不变,通过进化的方式改善种群中个体的质量,在可行域中搜索最优解。
典型的算法操作包括变异、修复、交叉和选择。变异操作釆用变异策略来生成变异个体,一般通过对上一代(父代)的差分操作,生成下一代(子代)的个体;修复操作的目的是使新生成的個体处于可行域内,保证生成的变异个体的可行性;交叉操作通过父代个体和子代个体的交叉策略来产生新的尝试个体;选择操作根据尝试个体和父代个体的评价函数来决定进入一下代种群的优秀个体。算法通过以上操作进行迭代计算,保证在每次迭代中淘汰劣质个体,保留优良个体,使得种群整体上向全局最优解区域靠近,优秀个体逼近全局最优解。具体的步骤包括:
(1)种群初始化。
首先在变量取值范围内随机生成初始种群,作为迭代初值,如式(1)所示:
从算法过程可以看到,有两个关键的参数:变异因子和交叉概率。文献[3]对交叉概率因子进行了研究,提出了自适应的交叉概率,取得良好的效果。而变异因子是决定父代个体变异程度的重要参数,一般变异因子取值在0~1之间。进行变异操作存在两方面问题,一方面,增加种群多样性,可加强全局搜索能力;另一方面,如果有效利用优秀个体信息,集中在优秀个体邻域附近搜索,可提升搜索效率,加强问题求解的收敛性。交叉操作是保持种群多样性的关键,交叉概率决定了尝试个体中变异个体所占比例,Cr取值一般为0到1。Cr越大,变异向量贡献越多,有利于局部搜索,加快收敛;Cr越小,初始向量贡献越大,有利于保持种群的多样性和全局搜索。
1.2 自适应变异方法
本文针对变异操作,考虑到进化初期需要增加种群多样性,可加强全局搜索能力;在进化后期,劣质个体逐渐被淘汰,优秀个体逐渐显现,如果集中在优秀个体邻域附近搜索,可提升搜索效率,加强问题求解的收敛性。为平衡这两个问题,本文根据进化进程的不同,提出一种自适应变异因子,如式(6)所示:
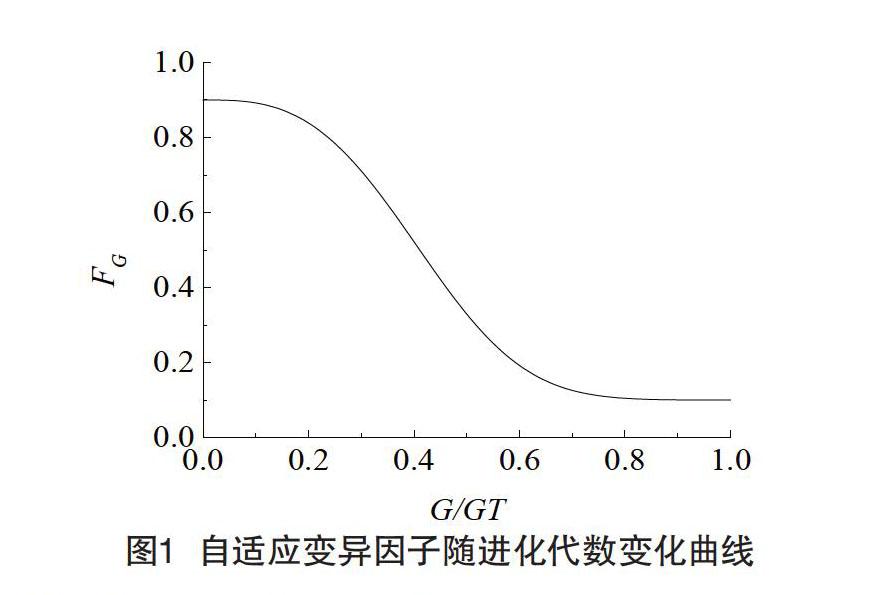
FG随进化代数的变化曲线如图1所示。可以看到,在进化初期FG较大,作为基向量的随机向量所占权重较大,此时全局搜索性能更高,能够广泛搜索最优个体;在进化后期FG较小,最优个体所占权重较大,此时集中在优秀个体邻域附近搜索,加强问题求解的收敛性。
2 计算结果分析
本文选取了4个经典测试函数[4]对本文提出的自适应变异因子进行测试。这4个函数的信息如表1所示,表中理论最优解f(a)=b表示变量取a时,函数达到最小值b,其中粗体表示向量。
将计算结果与差分进化算法中传统经典的DE/rand/1/bin和DE/best/1/bin进行比较,参考结果来源于文献[1]。为使得比较的公平性,本文采用该参考文献给出的计算条件,将种群规模设为100,最大函数评价次数设为50万次。统计30次独立运行的结果,以排除随机效应带来的影响,比较结果如表2所示。可以发现,本文提出的方法相对于传统差分进化方法,对测试问题具有更高的精度和性能。
为了测试本文方法的鲁棒性,将预设精度设置为10-6,最大函数评价次数设为50万次,如果在限定次数内达到预设精度,则认为程序成功求解。独立运行30次,统计函数平均评价次数及成功率,如表3所示。可以发现,本文的方法不论在函数评价次数上,还是成功率上,都较传统方法优秀。
3 结语
本文针对差分进化算法的变异操作,提出了一种根据进化代数的自适应变异方法。在种群进化前期,可增大种群变异,加强全局搜索能力;在种群进化后期,可限制在优秀个体附近搜索,加强局部搜索能力和问题的收敛性。数值结果表明,本文提出的自适应变异方法,符合理论预期,比传统的差分进化算法具有更优异的效果。
参考文献
[1] 肖婧.差分进化算法的改进及应用研究[D].哈尔滨工程大学,2011.
[2] 董明刚.基于差分进化的优化算法及应用研究[D].浙江大学,2012.
[3] 邓泽喜,曹敦虔,刘晓冀,等.一种新的差分进化算法[J]. 计算机工程与应用,2008,24(44):40-42.
[4] Suganthan PN, Hansen N, Liang JJ, et al. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization[D].School of EEE, Nanyang Technological University, 2005.

