“童化数学”教学的浅层倾向分析

薛正桧

摘要：儿童的数学学习要“童化”，但不能过度“童化”。局限于形式化的辨析，沉迷于特殊化的解法，热衰于单一化的训练，耽溺于简单化的推理，醉心于生活化的解读等，都是“童化数学”教学中常见的浅层倾向。看清这一点并迷途知返，能让我们在“童化数学”的道路上走得更坚实、更长远。

关键词：童化数学 浅层倾向 形式化 特殊化 单一化 简单化 生活化

数学是理性的，它高度抽象、概括，以最简洁的形式呈现于众，而儿童是感性的，他们的世界真实而具体，思维直接而富于经验。因此，儿童学习的数学，必须是经过加工的“童化”了的数学。学习的内容、学习的形式、学习的方法、学习的评价等都要童化。但童化不是目的，它只是儿童学习数学的一种手段、载体，童化的最终归宿仍然应是数学化。过度童化，是对儿童的一种妥协，是对学习本质的一种误解。基于此，笔者分析数学教学中几种常见的浅层倾向，有利于我们迷途知返，回归正确的方向。

一、局限于形式化的辨析

概念是小学数学学习的重要内容之一，是小学生学习其他数学知识的基础。对一个数学概念的完整辨析，包括内涵、外延两个方面，在内涵上要能切实把握概念的主要特征，在外延上要能准确区分概念的不同对象。按“童化数学”的要求，教学中我们会把概念的内涵分解，引导学生按要点逐一对照;或者从正、反两个方面给出大量的例子，带领学生逐一判断、说理。无论采用哪一种方式，都能极大地提高学生对概念的辨析能力。但凡事有利也有弊，过于精细化的处理极易步人形式化的误区。

二、沉迷于特殊化的解法

特殊与一般是两种既对立又统一的的思考方式。由特殊到一般、再由一般到特殊，是人们认识世界的基本过程。通常来讲，算术是特殊化的解题路径，代数是一般化的解题路径。小学数学以算术为主，强调局部，注重现象，对整体及本质的理解采用的是逐步深入、缓慢提升的方法。我们常常将问题特殊化（“童化”方式之一），先降低思维层级，然后再适时提升思维层级。但部分教师没能领悟教学的真谛，只重“解决问题”，不顾“问题解决”，解法沉迷于特殊化阶段，做法看似精明，实质剥夺了儿童进一步发展的权利，不可取。

三、热衷于单一化的训练

因为小学数学知识比较简单，相互间的联系不是非常紧密，解题的方法相对固定、缺少变化，这为教学中的批量训练提供了可能。对学生而言，只要训练不是机械、重复的，他们都乐此不疲。在富有童趣、充满竞争的氛围中，学生收获了成功、收获了喜悦。但不可否认的是，这种训练如果不能高瞻远瞩，不能指向更广阔的思维空间，就是一种低层次的能量消耗。

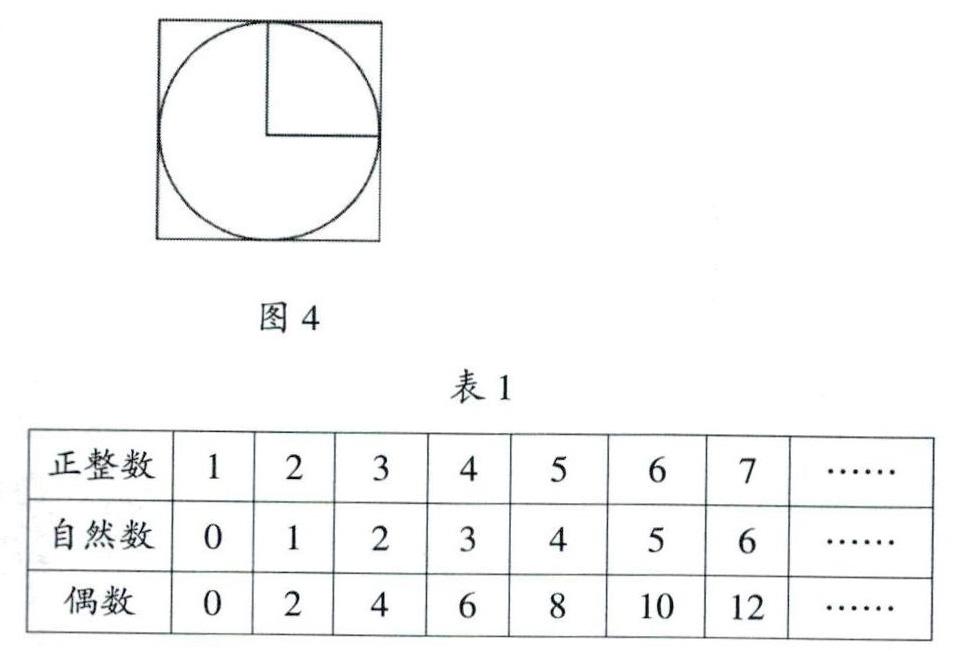
案例3：如图4，已知外正方形的面积是20平方厘米，求圆的面积。

由于学龄的阶段性特点，小学阶段不教学开平方的内容（个别利用乘法口诀表的除外）。在圆的面积教学中，常见的有三种类型，一是根据半径求面积，二是根据直径求面积，三是根据周长求面积。正是基于这样的原因，一些教师不经意间就侧重了对这三种题型的单一化训练，而置其他方法于不顾。多次强化以后，学生自然会认为只有这三种情况才能求出面积，路径单一而缺乏变化。面对图4这样的问题时，因为超出了平时训练的范围，学生束手无策也就在所难免了。其实，已知“半径的平方”一样可以求出圆的面积。教学就是这样，框得越死思维就越狭窄，放得越开思维就越开阔。

四、耽溺于简单化的推理

小学阶段的推理主要是归纳推理，即从一些个体现象中发现一定的规律。归纳推理是合情推理的一部：分，有正确的，也有错误的。小学生由于思维发展的不健全，一些看似合情的推断却不一定合理，这就要求教师多加区分、引导，不能被儿童所同化。

案例4：偶数的个数是自然数个数的一半。

学生是怎么得出这个结论的呢？原来他们发现：0～9中，偶数的个数是总个数的一半;10-19中，偶数的个数是总个数的一半;100-999中，偶数的个数也是总个数的一半;等等。换个角度看，从0开始，总是“偶数、奇数”“偶数、奇数”这样两个一组依次排列的。所以，在所有的自然数中，偶数占一半，奇数占另一半。表面上看，论证有据，句句在理，其实不然。如果：一个集合A能与正整数集建立一一对应的映射，则称集合A是可数集，可数集之间可以比较元素的多少。照表l那样，自然数集和偶数集都与正整数集建立了一一对应的映射且趋向于无穷。因此，用康托集合论的观点来看，偶数的个数与自然数的个数是相等的。而儿童的错误就在于他们以有限替代了无限，“想当然”地把问题简单化了。

五、醉心于生活化的解读

数学最终是要去情境化的，但它并不排斥情境，从情境中来，到情境中去。尤其当某些知识生涩难懂，某个问题无从下手时，辅之以情境，把问题生活化，儿童便能从个体的生活经验中汲取营养，找到理解的支撑点或解题的突破口。生活的边界就是儿童数学学习的边界，儿童的数学学习应该建立在已有的学习、生活经验之上。但必须要澄清的是，数学和生活不能完全划等号。我们将数学生活化，其实只是对数学的一种个性化解读，这种解读应以不违背数学的本来面目为原则。

案例5：13名小伙伴相约去公园划船。每条船租金30元，限坐6人。他们至少要付多少元？

这是一道生活味道很浓的策略类问题，它的数学模型是有余数除法中商的取整问题。正确的解法是：13÷6=2（条）……1（人），2+1=3（条），30×3=90（元）。从生活的角度来理解，就是剩下的1人也得租一条船。但有些学生生活的经验很足，头脑灵活得很，说可以让剩下的1个人到前面2条船上去挤一挤，这样租两条船就够了，只要花30×2=60（元），并煞有介事地提议让“瘦子们”挤在一起。另一位学生说，挤是有危险的，应该让他和其他租船的人拼船，这样再多花1个人的钱就行了，30÷6=5（元），共花60+5=65（元）。这样思考可以吗？如果仅仅是生活中的一个实际问题的话，后两种思路有合理的成份，或许也行得通。但作为数学题，这么想就不对了，数学题有其自身的规范及格式，“13名小伙伴”“限坐6人”等是条件，是不可更改的，“至少”是要求，尽量满足，如果都去曲意解读、自由发挥的话，那数学就不能成为数学了。

儿童学习数学，童化是前提，是起點，是对他们当下水平的肯定与利用;数学化是本质，是归宿，是对她们未来水平的期待与发展。

【责任编辑：陈国庆】