基于MATLAB的直流无刷电机模糊PID控制设计

杨昕红，刘长文

(1.沈阳职业技术学院，辽宁沈阳 110045；2.沈阳大学，辽宁沈阳 110044)

0 引言

直流无刷电机性价比优良，在机电产品制造领域得到了较快的发展和应用。直流无刷电机在质量和体积方面实现了小型化、轻量化，在反应速度、工作效率、节电节能及运行精度等方面超过其他种类的电机。机电领域应用产品的快速发展，对直流无刷电机的控制方法与理论提出了更高要求。当前对于提升直流无刷电机控制系统精度已经成为首先需要解决的问题。

直流无刷电机控制器是电机系统中的核心器件，在电机系统中将控制策略(控制规律)与控制器的合理配置，是整个系统中的重要环节。在经典控制理论中，PID控制规律是极其重要的一种控制算法。但是当被控对象的特性参数受负荷扰动影响以及环境变化时，传统PID略显不足。本文所研究的模糊PID运用智能控制的方法，将专家经验总结同时存入计算机，随着机电设备运行环境而变化，控制系统计算机能自动调整PID 的参数值。实验表明，基于模糊PID的控制系统明显具有响应速度快、超调量小的特点，其稳定性和鲁棒性更强。

1 直流无刷电机模型

无刷直流电机有定子和转子组成，通过改变定子绕组上的电流波频率及其波形，从而控制转子的运行状态，其定子电压平衡方程为

(1)

式中:ei为定子反电动势；ii为定子电流；U1为定子各相电压；Ri为定子各相绕组电阻；Li为定子绕组间自感；Lij为定子绕组间互感。

首先建立直流无刷电机数学模型，设想三相绕组间互感为零时，即相互之间没有互感，可以得到如图1所示的等效电路。

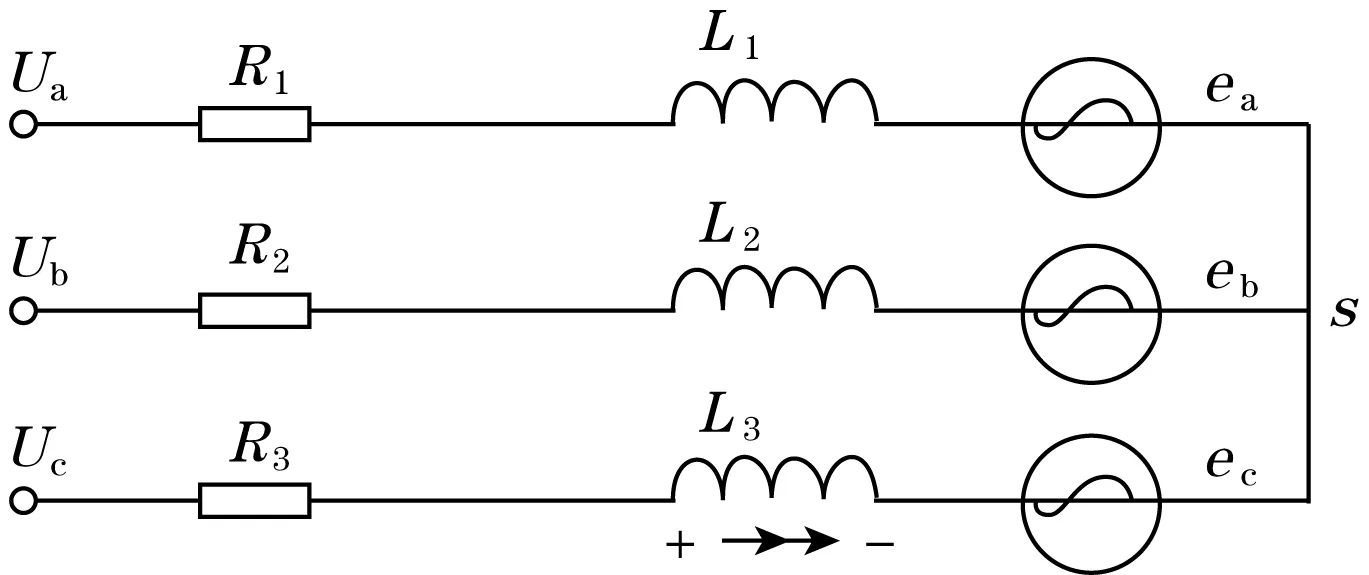
图1 相间互感为零时的等效电路图

2 模糊PID原理

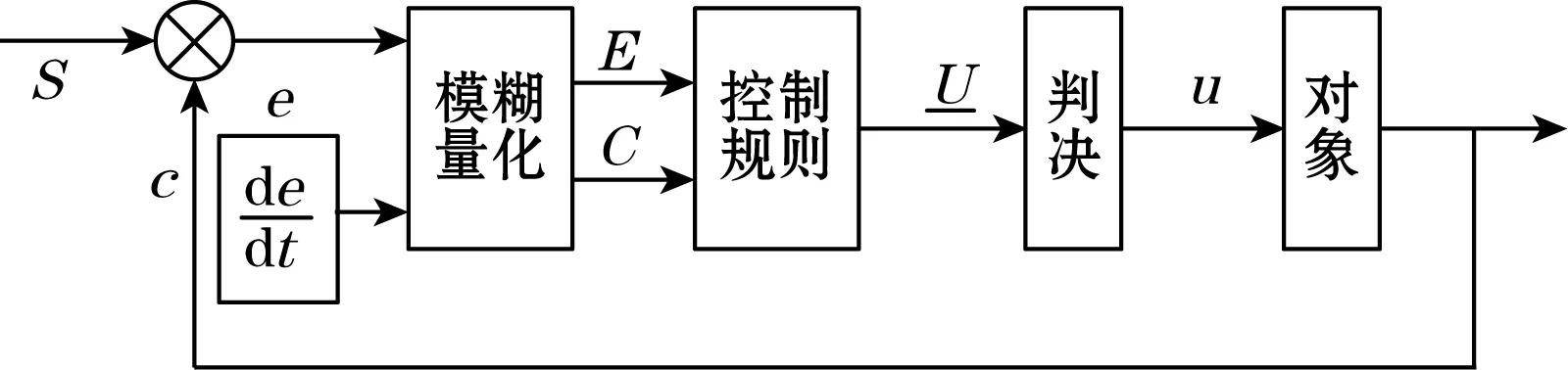
图2 模糊控制结构框图

3 控制系统设计

本文以STM32为控制器核心处理器，设定控制系统给定值为单位阶跃函数，按照PID模糊控制[12]要求，控制系统输入包括误差e和误差变化率ec，从而构成PID参数模糊逻辑控制器，控制系统结构如图3所示。

图3 控制系统结构图

4 系统仿真分析

4.1 利用MATLAB中的Simulink工具进行Fuzzy control设计研究

在现场环境应用中，一般选择以PI为主要控制规律，其步骤如下：

4.1.1 设置模糊语言变量

添加模糊变量、添加隶属度函数和添加模糊规则。

4.1.2 模糊控制表

模糊控制表来自于研究设计人员的理论分析和操作人员的实际调整经验组合，查阅资料便可得到与Kp和Ki分别对应的模糊规则表。

4.1.3 输入参数的模糊化

对于模糊控制来说，须将模糊变量设定在研究论域中，本文的模糊集及论域定义如式(2)、式(3)所示。

e={NB,NM,NS,ZO,PM,PB}ec={NB,NM,NS,ZO,PM,PB}

(2)

式中：NS为负小；NM为负中；NB为负大；ZE为扩充零；PS为正小；PM为正中，PB为正大。

通过采用高斯隶属度函数(Gauss MF)，利用MATLAB可以计算出各模糊子集的隶属度函数值。根据相应的模糊规则求得对应的函数值，再利用MATLAB的FUZZY工具得到PID参数的模糊规则方阵，代入下列各式进行计算：

(4)

(5)

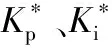
模糊PID最大的优点是可自适应调整参数Kp、Ki和Kd的值，将这些参数进行最优处理以便达到最佳的动态控制效果。

4.2 采用MATLAB进行仿真研究

阶跃输入对系统来说比较苛刻的输入函数。假如在这种情况下，系统的稳定性能以及动态性能都能达到预期的效果，那么系统在其他函数形式下也会得到令人满意的结果。模糊PID系统在控制中的模糊语言变量包含，添加隶属度函数、添加模糊变量和添加模糊规则。其中，添加的隶属度函数基于高斯型隶属函数，其数学模型为

本文所研究的被控对象为

(6)

4.2.1 采用常规PID的MATLAB仿真

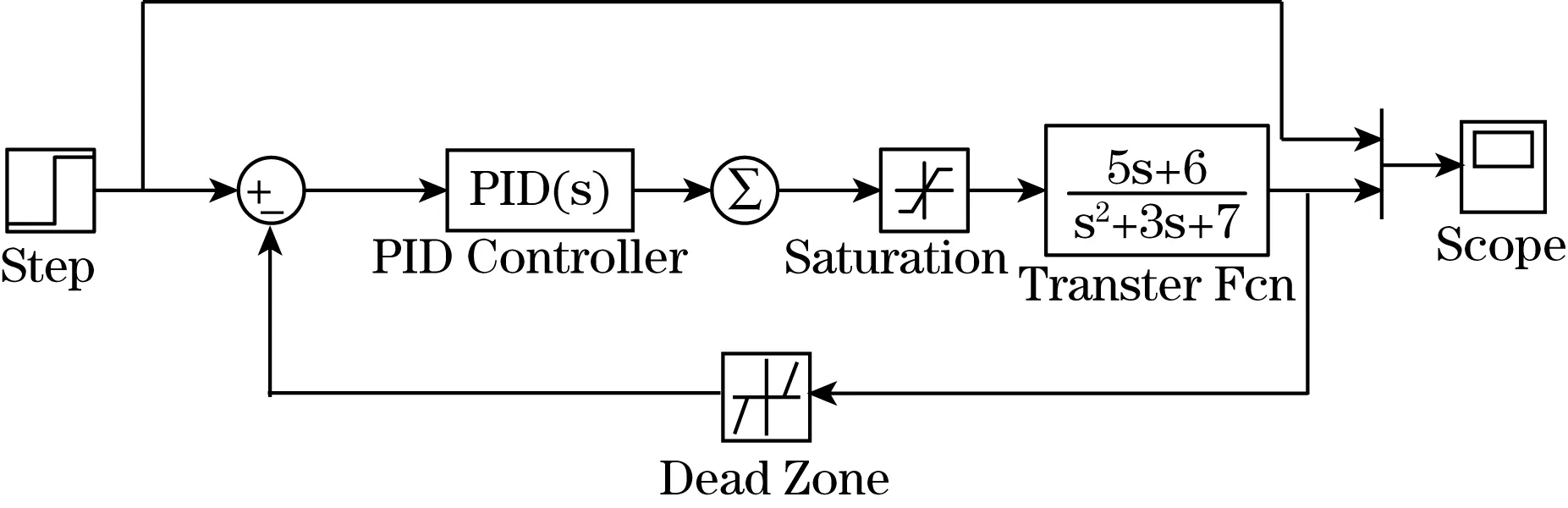
图4 常规PID的MATLAB仿真

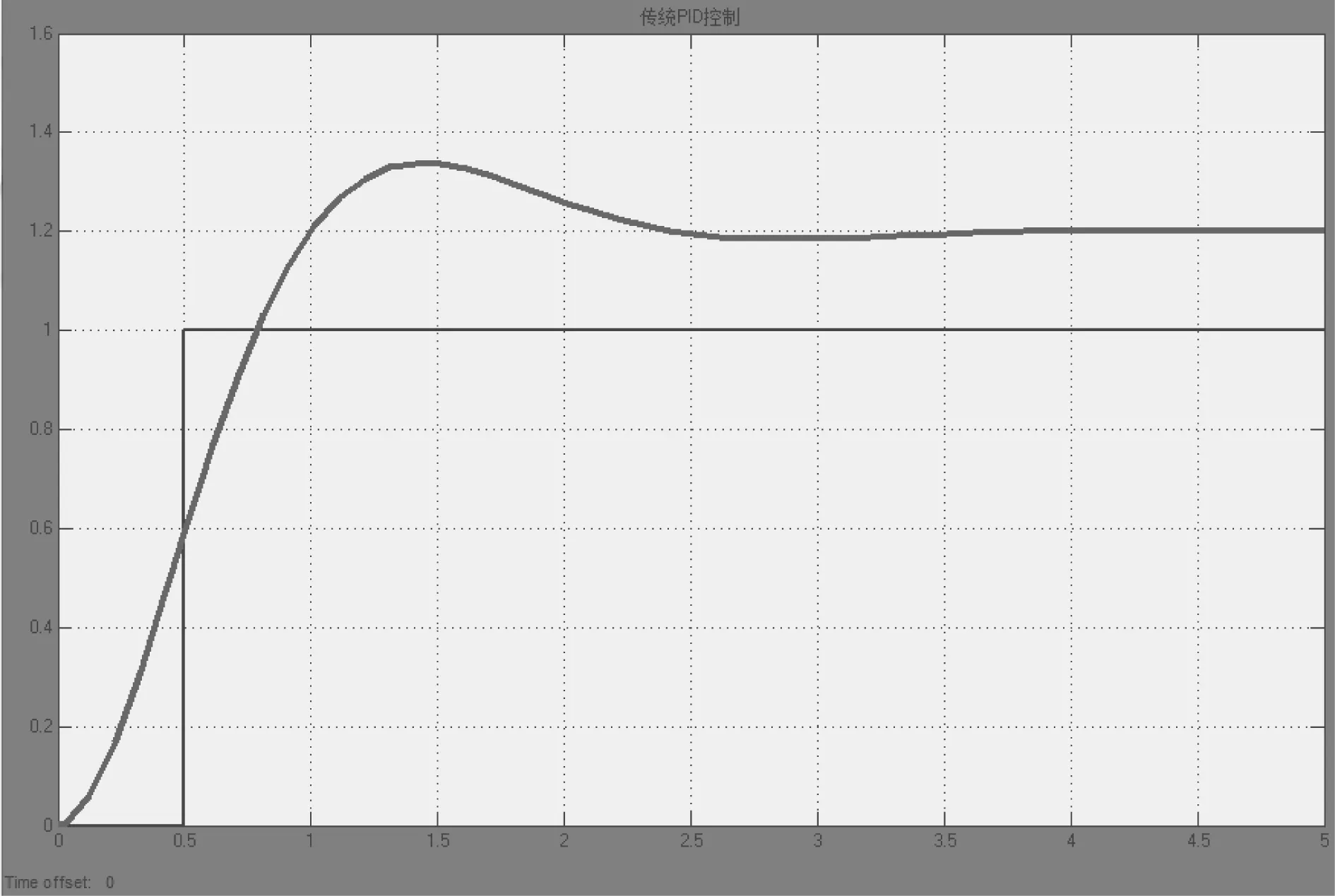
图5 常规PID单位阶跃响应

4.2.2 采用模糊控制器的设置

模糊控制器的FIS编辑设计界面中，采取双I/O模式，建立模糊规则表Kp和Ki，输入量设置为误差e和误差变化率ec，输出量设置为Kp和Ki，模糊控制器设计界面如图6所示。

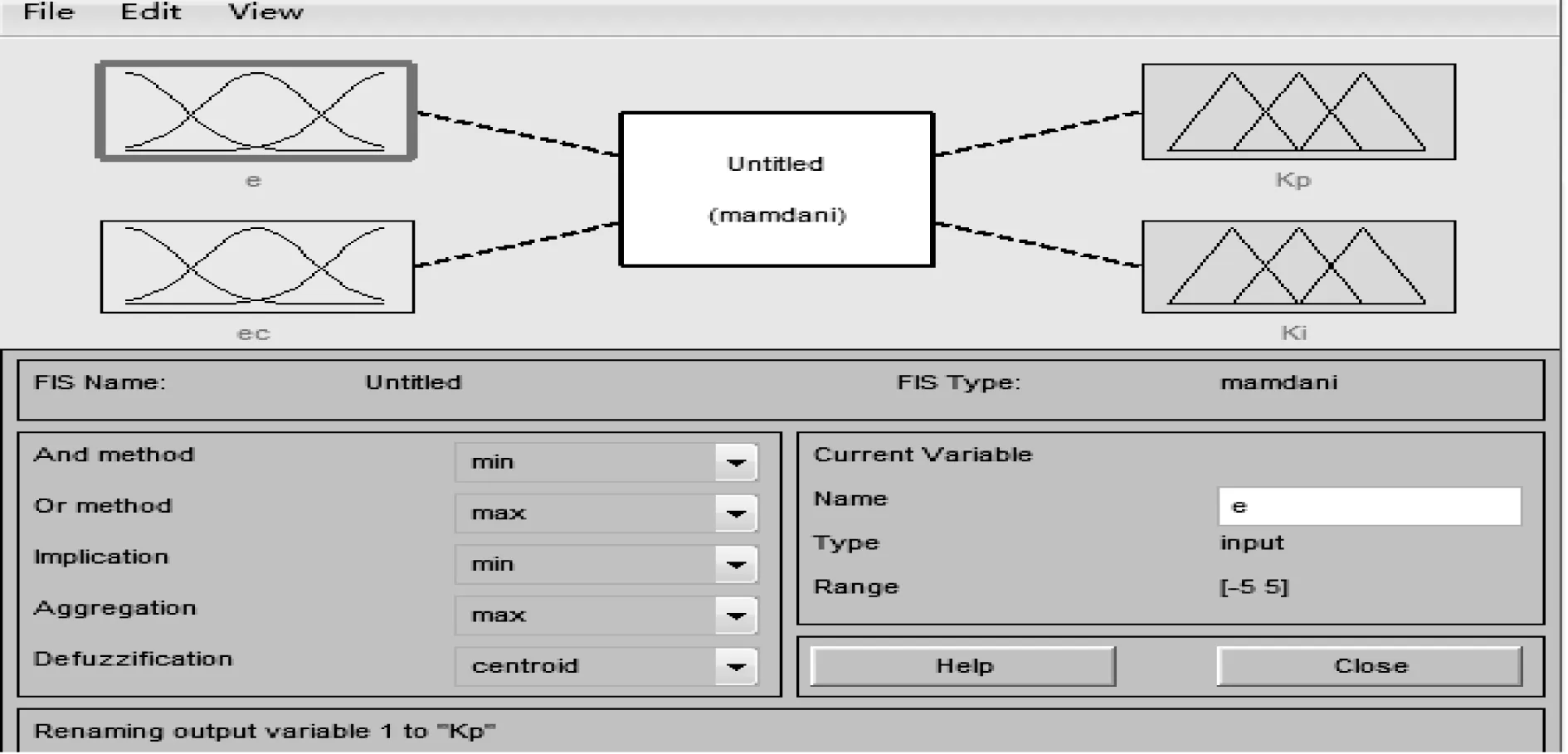
图6 模糊控制器的设计界面

选择Gauss MF为模糊语言的隶属度函数，确定模糊规则，一条模糊规则就是一条陈述语句，其模型为：IF<模糊命题>,THEN<模糊命题>。系统仿真分析中显示一共产生28条模糊规则，控制经验表产生的模糊规则如图7所示。推理观察过程如图8所示。图9(a)为Kp控制量与误差e和误差变化率ec的变化关系图，图9(b)为Ki控制量与误差e和误差变化率ec的变化关系图。

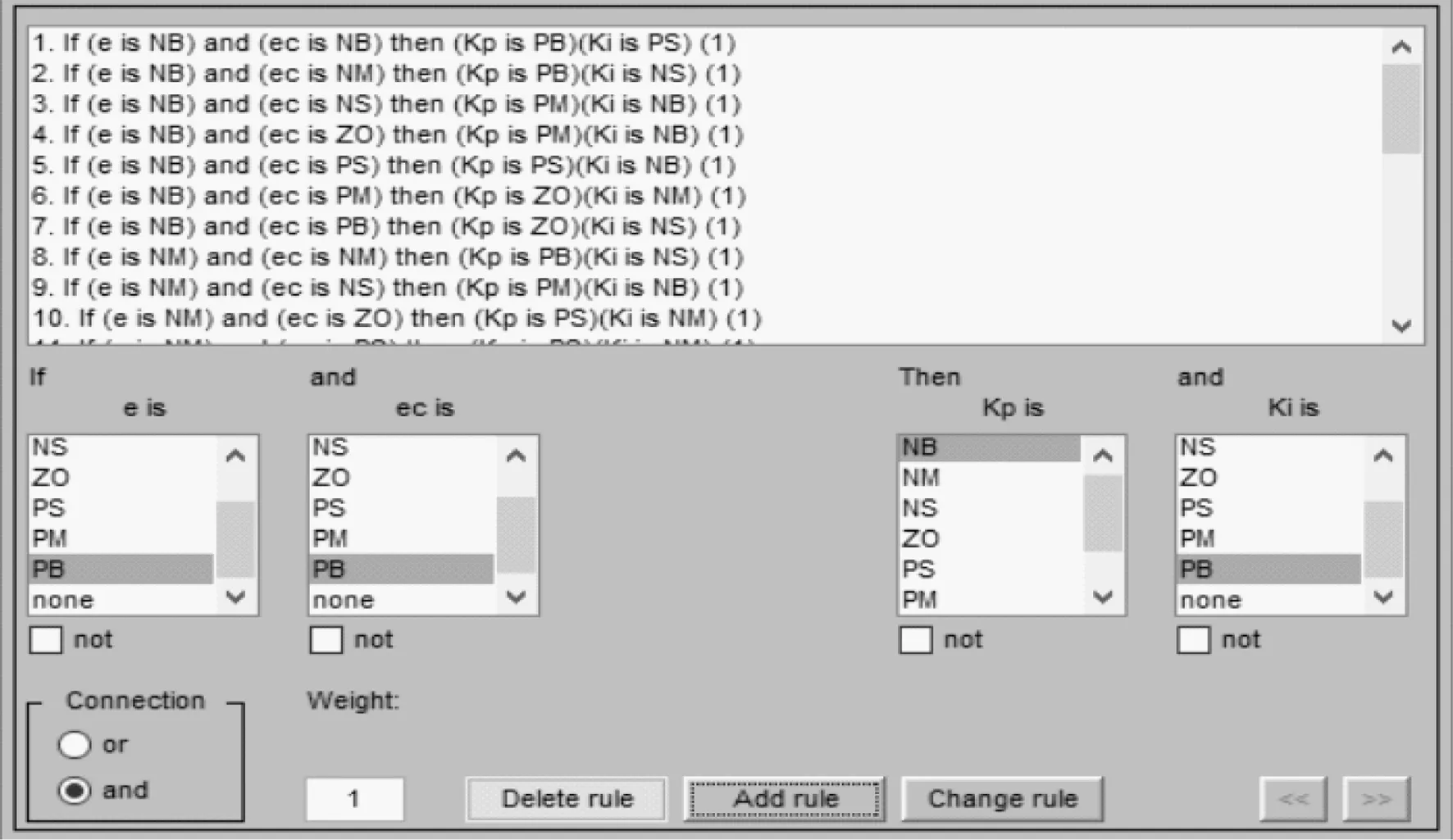
图7 产生的模糊规则

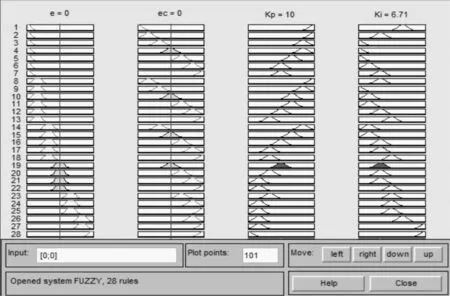
图8 模糊推理过程

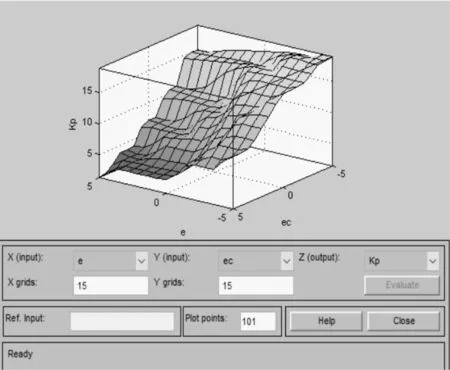
(a) Kp与误差e、误差变化率ec间的变化关系

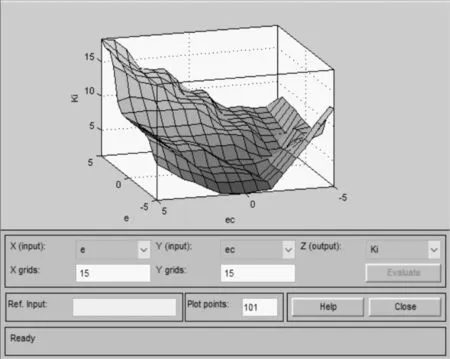
(b)Ki与误差e、误差变化率ec间的变化关系图9 各输出变量与误差e、误差变化率ec间的变化关系

4.2.3 Simulink模型的建立

利用模糊子系统的方法，建立Simulink仿真模型如图10所示。

图10 Simulink的模糊PID仿真结构图

如图10中所示，设计Subsystem子系统，在子系统中的Fuzzy logic control且输入模糊规则，文件名‘fuzzy.fis’，运行图10所示的系统模型，可以输出模糊PID的仿真结果，如图11中(b)所示。

(a)传统PID作用下

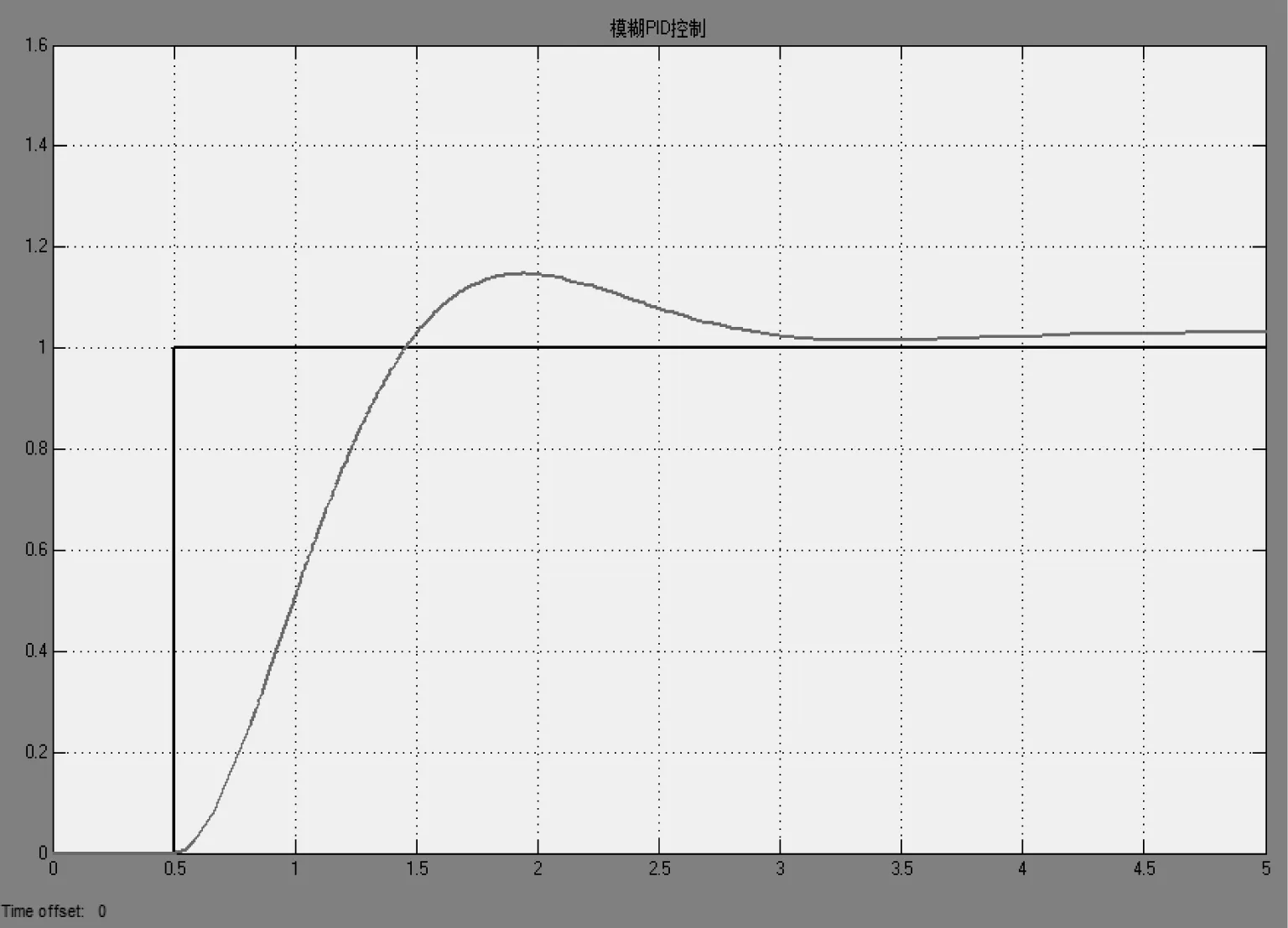
(b)模糊PID作用下图11 PID的输出仿真结果

表1 控制系统各项性能对比

5 结束语

比较图11和表1，对于非线性、无法确定准确数学模型或电机运行环境复杂多变，导致被控对象参数易发生变化的场合，基于MATLAB的直流无刷电机模糊PID控制设计，较好地解决了电机系统适应性问题，通过改进传统的PID电机控制理论，模糊PID控制设计方法，实现了对非线性机电设备的控制，同时显示了系统稳态误差、超调量、精确度等方面较强的优势,确保了控制系统的稳定及鲁棒特性。