高精度的科氏流量计频率估计方法及应用

沈廷鳌,李 明,罗媛媛,陈丽薇

(1.陆军勤务学院，重庆 401311；2.四川泰利工程项目管理有限公司，四川成都 610023)

0 引言

科氏流量计可直接高精度地测量流体质量流量，已在石油、化工等行业得到广泛应用[1]。科氏流量计流量测量的关键在于准确估计出信号的频率和相位。然而，受流体流速、噪声干扰等因素影响，流量信号呈现缓变特性，进而要求对流量信号进行实时精确估计。

由科氏流量计测量原理可知，频率估计是实现高精度流量测量的首要步骤。现有科氏流量计频率估计方法主要有：DFT法[2]、CZT法[3]、数字锁相环法[4]、自适应陷波滤波法[5]等。相比于其他频率估计方法，自适应陷波滤波法可以根据被测信号特点，自动调整参数，实现频率的估计和跟踪[6-7]。但该方法初始参数值的设定较敏感，难以兼顾收敛速度和长时跟踪精度，限制了该方法的应用推广。

为克服陷波器的收敛问题，采用FFT法对信号进行短时频率估计，然后，利用负反馈控制原理，通过设置一个评价因子来实时监测调整陷波参数，实现信号频率的长时跟踪，进而提出一种高精度的科氏流量计频率估计新方法。在自适应陷波器原理及其问题分析的基础上，阐述了所提方法的基本思路、具体措施和实现步骤，并利用MATLAB仿真与原有方法进行了比较分析。仿真分析和工程应用均表明所提方法可实现高精度频率估计。

1 自适应陷波器原理分析

1.1 自适应陷波器原理

自适应陷波器通过利用前一时刻的滤波参数来对当前时刻的滤波参数进行调节，以适应未知信号和噪声变化的统计特性。理想陷波器的频率特性只在陷波频率处等于1，其他处均为0[8]。其实现方式如图1所示[8-9]。

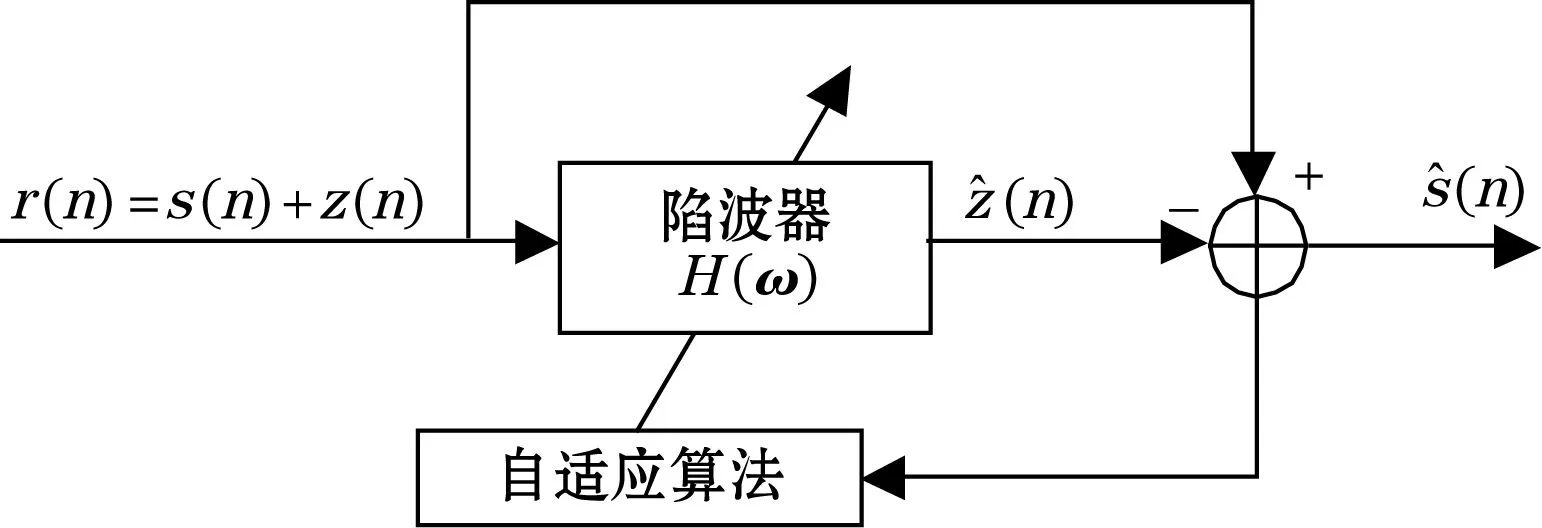
图1 自适应陷波器结构

1.2 问题分析

1.2.1 收敛问题

由陷波器原理可知，在输入信号先验知识未知时，初始陷波带宽往往较大，以便能尽快捕捉到信号频率。但陷波器带宽越宽，陷阱越大，滤除的噪声就越少，频率估计精度就较低。随着陷波参数的不断调整，陷波器会逐渐锁定在正确频率上，陷阱宽度会逐渐缩小，滤除的噪声会越来越多，频率跟踪的精度会越来越高。陷波器从开始逐渐跟踪锁定到正确频率的过程可视为收敛过程，该过程中的频率估计精度较低。

为提高陷波器收敛过程的频率估计精度，收敛过程期间可采用其他频率估计方法替代。本文采用FFT法快速估计出频率估计值，同时将估计值赋予陷波参数，以便于使陷波器尽快锁定在正确频率上。同时，收敛期间的频率估计值以FFT法的参数估计值为准。

1.2.2 长时跟踪问题

采用陷波器跟踪信号频率，在输入信号频率未知时，为尽快捕捉到信号频率，初始陷波带宽往往较大。随着陷波参数的自适应调整，收敛因子趋近于1，陷波带宽趋近于0，频率估计精度会越来越高。当陷波带宽趋近于0时，若信号频率的变化跳出了陷阱的宽度，即频率值不在陷阱内，就会导致陷波器无法锁定在一个正确的频率估计值上，进而出现较大的频率估计误差。

长时跟踪过程中，随着陷波器参数的不断调整，陷阱宽度会逐渐缩小，当陷波带宽趋近于0时，就会容易出现频率的变化跳出陷阱宽度的情况，导致陷波器无法感知到信号频率的改变，进而出现较大的频率估计误差，该情况可视为长时跟踪问题。

为提高陷波器长时跟踪的频率估计精度，当陷波器带宽趋近于0时，可设置一个评价因子来实时监测调整陷波参数，为确保频率值在陷阱范围内，防止陷波器失去自适应能力，可通过重新增加陷波带宽的办法进行改进。

2 科氏流量计频率估计方法

2.1 基本思路

由上述分析可知，陷波器存在难以兼顾收敛速度和长时跟踪精度的问题，为此，提出一种高精度的科氏流量计频率估计新方法，即：首先采用FFT法估计流量信号初始频率，然后将估计出的信号频率值赋予陷波器作为其初始频率，在陷波器未收敛稳定之前(假设陷波器的稳定点在M点)，仍将FFT法的估计频率做为频率估计值，待陷波器稳定之后(在M点后)，将陷波器的估计频率做为频率估计值。

需要说明的是，只有当陷波器稳定后，即锁定在正确频率上之后设置评价因子才会起作用。

2.2 具体措施

2.2.1 收敛问题

采用FFT法对流量计信号进行短时频率估计，将频率估计值赋予陷波器作为初始参数，可提高陷波器的收敛速度，其具体算法如下：

设流量信号为单频正弦信号：

s(t)=Acos(2πf0t+θ0)

(1)

式中：A、f0和θ0分别为信号的幅值、频率和初相位。

f0一般表示为

f0=(k0+δ)·fd

(2)

式中：k0为正整数；δ为泄漏误差系数，|δ|≤0.5；fd为频率分辨率，fd=fs/N；fs为采样频率；N为采样点数。

对信号进行采样，可得到：

s(n)=Acos[2π(k0+δ)·n/N+θ0]

(3)

对s(n)进行DFT变换，只计算正频率部分[10]，可得：

(4)

S(k)幅度最大值处离散频率的索引值记为k1，k1=int[f0T]；int[x]为取最接近x的整数。对于较大的N，在幅度最大值处，S(k)的幅度可近似为

(5)

式中：δ=(f0-k1Δf)/Δf为信号频率与幅值最大值处对应频率的相对偏差；Δf=1/T。

在紧靠k1的左侧与右侧的两条谱线中幅值较大处(称为幅度次大值，对应的离散频率索引值为k2，k2=k1±1)，S(k)的幅度可近似为

(6)

A2与A的比值记为α，可得：

(7)

根据A2与A1的比值可得到|δ|的估计值：

(8)

根据δ值，通过对离散频谱得到的估计值f0进行插值，从而可得到更为精确的频率估计值为

(9)

式(9)中，根据k2的位置来确定符号，若k2=k1+1取加号，反之取减号。

2.2.2 长时跟踪问题

利用反馈控制原理，通过设置一个评价因子来实时监测调整陷波参数，实现信号频率的长时跟踪，其具体算法如下：

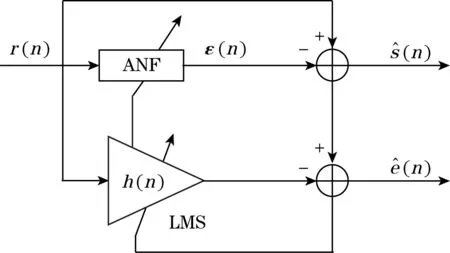
图2 改进陷波器结构

h(n)可由LMS算法计算得到[11]，结合图2可得：

(10)

式中μh为步长。

h推导过程如下：

(11)

由于存在:

(12)

2.3 实现步骤

根据上述基本思路，所提方法实现步骤如下：

(1)在流量信号频率未知的情况下，首先采用FFT法快速检测信号频率。

(2)将FFT法的频率估计值赋予陷波器作为其频率估计初值，陷波器开始工作，同时，以FFT法的估计值作为频率估计值；该过程既可以加快陷波器的收敛过程，也可提高该阶段的频率估计精度。

(3)待陷波器工作稳定后，FFT法就停止工作，改由图2所示的改进陷波器独立跟踪信号频率，将改进陷波器的频率估计值作为频率估计值。

整个算法的实现流程如图3所示。

图3 本文方法频率估计实现流程

综上分析可知，本文方法可实现对未知信号频率的快速、长时、高精度估计。

3 仿真分析

为证实本文所提方法的有效性和普适性，将所提方法分别应用于格型陷波器[12]和SMM陷波器(新式ANF)[13]，并在MATLAB环境中与原有方法进行了对比分析。

设输入信号模型为

r(n)=A(n)sin[ω(n)+φ(n)]+σee(n)

(13)

式中：A(n)为幅值；ω(n)为归一化角频率；φ(n)为相位。

A(n)、ω(n)和φ(n)按照随机游动模型变化。时变信号模型及各自陷波参数选取详见文献[12-13]所示。本文方法中，评价因子参数Th=0.05,μh=0.01。

图4为采用本文所提方法对格型陷波器改进前后的频率估计比较图，图5所示为采用本文所提方法对SMM陷波器改进前后的频率估计比较图。为证实本文所提方法的普适性，图4和图5的曲线均为随机产生所得。

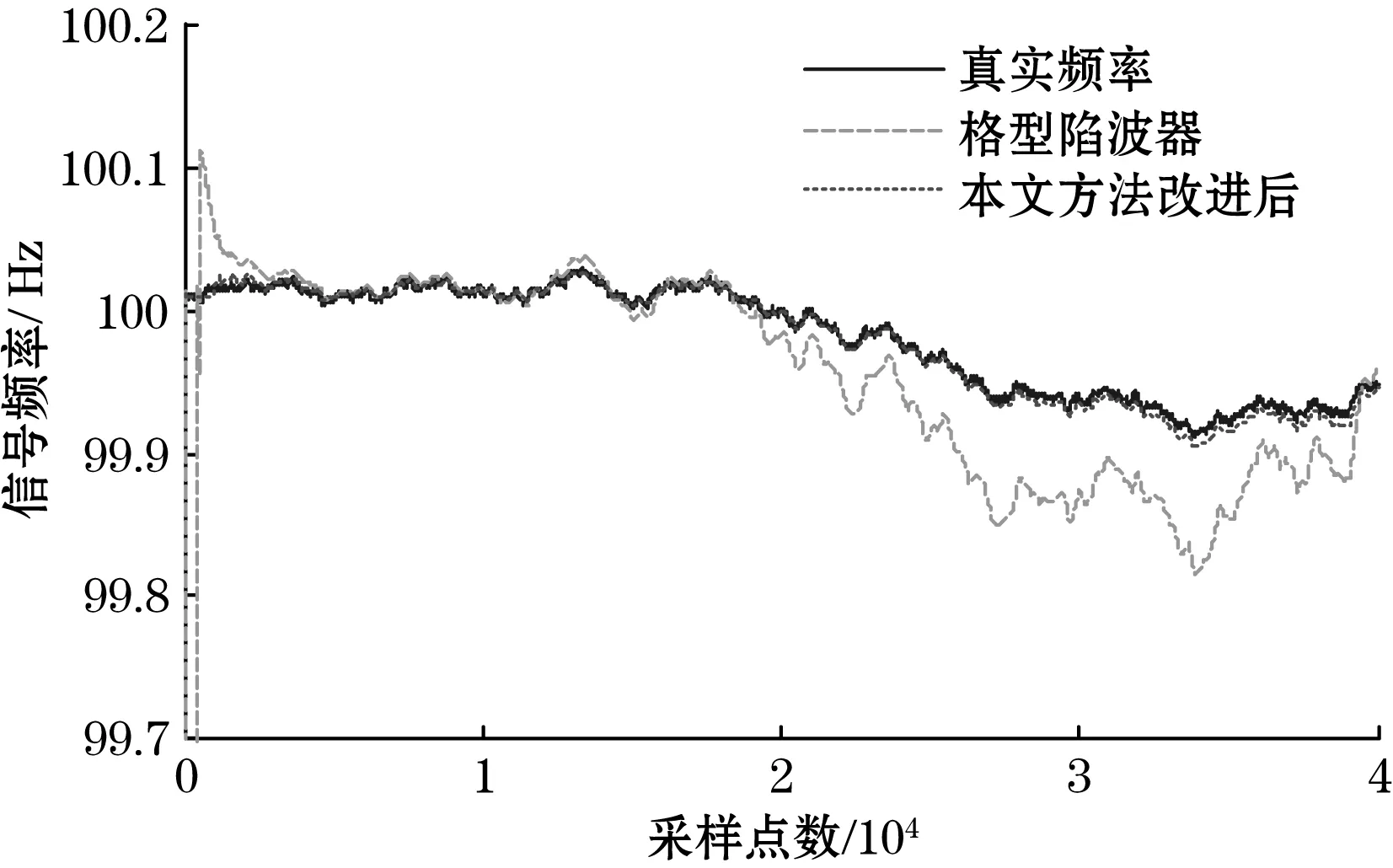
图4 本文方法与格型陷波器频率估计的比较

图5 本文方法与SMM陷波器频率估计的比较

从图4和图5均可以看出，不论是格型陷波器，还是SMM陷波器，均存在收敛过程和长时跟踪过程估计精度较差的问题，与原有方法相比，采用本文方法改进后的频率跟踪曲线均能较好地与真实频率变化曲线吻合，与原有方法相比，本文方法整个频率跟踪过程均保持着较高的估计精度，既克服了收敛过程的影响，又解决了长时跟踪问题。此外，从图4和图5还可以看出，本文方法适用于多种陷波器，且对任一随机产生的曲线均保持着较好的跟踪效果，更具普适性。

4 工程应用

为进一步证实本文所提方法的有效性，图6所示为科氏流量计实验平台，采集流量计输出的两路振动信号，分别采用格型陷波器、SMM陷波器和本文方法(此节方法是在格型ANF基础上改进)来估计信号频率。流量计振动信号频率约为146 HZ，采样频率为10 kHz。针对不同的流量分别进行采样，每个流量采样40 000点/路。图7为格型ANF、新式ANF和本文方法估计频率比较图，由于传统陷波器存在收敛过程和长时跟踪问题，采样数据取2 000至20 000点。由图7可以看出，3种方法估计结果相近，与图4和图5仿真结果类似，证实了3种方法的有效性。由于现有技术的限制，无法得到每一时刻信号真实频率，采用频率估计精度较高的基于矩形窗的比值法来估计频率，将其作为参考值来评判三种方法。

图6 科氏流量计实验平台示意图

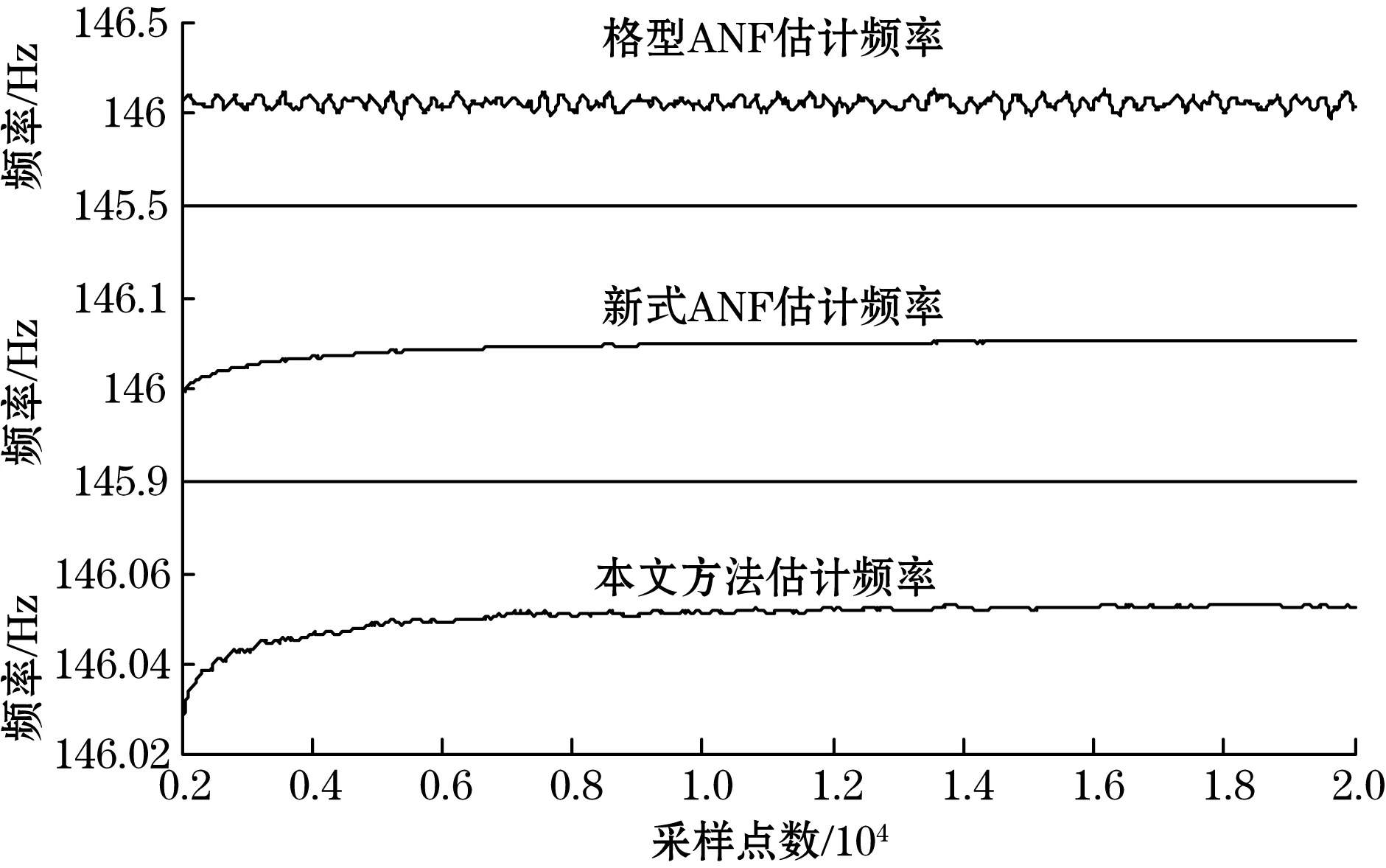
图7 3种方法估计频率的比较图

表1列出了相同数据段在不同流量下分别采用格型ANF、新式ANF和本文方法估计频率得到的均值比较。由表1可以看出，本文方法的频率估计值与参考值最接近，从而也证实了本文方法的实用性。

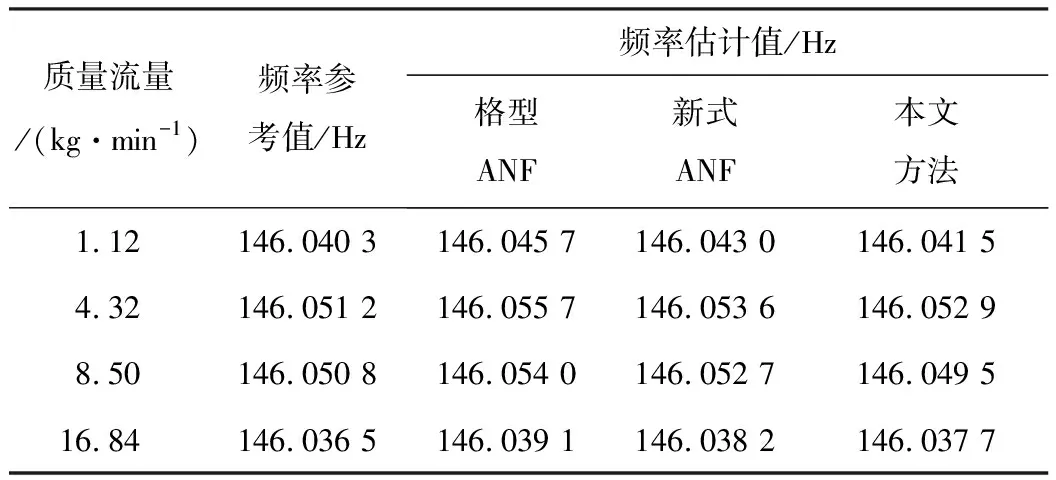
表1 相同数据段在不同流量下频率估计均值的比较

5 结论

为提高科氏流量计测量精度，解决自适应陷波器存在的收敛问题和长时跟踪问题，提出了一种高精度的科氏流量计频率估计新方法。仿真分析表明本文方法具有如下特点：

(1)在起始阶段，采用FFT法估计流量信号频率，克服了收敛过程频率估计精度较差的问题，同时，将FFT法估计的信号频率值赋予陷波器作为其初始频率，加快了陷波器的收敛。

(2)利用负反馈控制思想来设置评价因子，有效地解决了陷波器的长时跟踪问题。

(3)所提方法频率精度更高，可参考应用于其他类型的自适应陷波器，普适性更强。