关于电磁波特性的一组新方程

黄志洵

(中国传媒大学信息工程学院，北京100024)

1 引言

人们对事物的认识从来都不是一两次就可以完成的，因此科学研究是一个过程，总是在讨论、质疑的反复中波浪式推进。例如在宏观层面上，虽然媒体常报道“发现了××黑洞”的消息，也常见到“存在黑洞是广义相对论的必然结果”的论文，但仍有许多学者不相信自然界中有黑洞。仅笔者所知，持此观点的就有英国物理学家S.Hawking，美国物理学家G.Chaplin，中国物理学家艾小白等人，后者还是我多年的挚友。艾小白认为，许多研究看起来不错，但距离物理真实太远；笔者同意他的观点。

在微观层面，欧洲于2008年启用大型强子对撞机(LHC)，可以把质子加速到14TeV能量，其环形管道周长27km，安装了许多能产生强电磁场的超导磁铁。从理论上讲，根据Heisenberg测不准原理，14TeV的质子探针应能探测到(10-18～10-17)cm的空间尺寸。……我们知道，在早期由于弱电统一理论与规范对称性出现矛盾，为了挽救标准模型英国人P.Higgs提出有一种玻色子可以传递真空标量量子场与其他粒子之间的相互作用(从而使各种基本粒子有了质量)，这叫Higgs粒子；发现该粒子的任务交给了LHC。……必须指出，粒子质量问题是物理学中一个恒久不变的话题，很多基本问题至今得不到回答；例如：电子、质子的惯性质量是如何演化出来的？电子质量与质子质量为何相差那么大？等等。……在本文中我们将把目光聚焦到光子质量的问题上，那也是一个至今没有解决好的难题。本文是对文献[1]的丰富和补充。

2 如何看待波动与物质的关系

Newton力学中的物质，有形状、大小、质量和密度，受力后会运动并在3D空间描出其轨迹。波动却没有Newton定义的那种质量，不能用力使其加速。波展布于广大的空间，要作精确描述需用其他方法(波方程就是一种方法，现代电磁理论中的并矢Green函数、矢量偏微分算子等数学工具是另外的方法)。当然波科学的理论还没有完全搞清楚“波(动)粒(子)二象性”问题。作为最简单的理解，我们只能说光具有波粒二象性。有质量的实物粒子(如电子)也有波动性的一面，称为物质波或de Broglie波。de Broglie波关系式为

(1)

(2)

E、p为粒子的能量、动量，f、λ为对应的物质波频率和波长。应当指出，对于光，有以下方程：

fλ=c

(3)

因此两个关系式并非互相独立，实际上只有一个关系式；对实物粒子而言两个式子则是彼此独立的。

1926年上半年E.Schrödinger[2]创造了量子波动力学，即QWM；其核心是描述微观粒子体系运动变化规律的基本运动方程——Schrödinger方程。M.Planck认为该方程奠定了量子力学(QM)的基础，如同Newton、Lagrange和Hamilton创立的方程在经典力学(CM)中的作用一样。所谓含时的Schrödinger方程(SE)是他在1926年6月提出的，其形式为

(4)

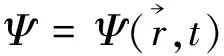
有的物理学家心存疑虑，认为用SE讨论光子运动存在一个困难——方程中的m如何取值？传统上认为光子是静止质量为零的中性粒子，但如把m=0代入SE，它将不再有任何意义。笔者认为，说“光子静质量为零”只是理论家的一种观点或推论，并未被实验所确证。有的物理学家(例如美国的R.Lakes[4])认为“the photon is massive”，并开展实验以测量光子静质量。从测不准关系式出发可估算最小可能的光子静质量m0=10-66g[5]，今天的实测值虽越来越小但离此尚远。将来即使测到这个水平，也不能确定光子是否有静质量。……反过来说，光纤技术中应用SE已经成功，是否可以推断光子的m0≠0？这是值得思考的。

当我们考虑波动时，必须历史地看问题，知道最早是由于数学家的贡献。波动力学(wave mechanics，WM)可以认为在1760年时就有了；166年后(即1926年)由Schrödinger创立了量子理论的波动力学。因此前者可称之为经典波动力学(classical wave mechanics，CWM)，后者可称为量子波动力学(quantum wave mechanics，QWM)。先看CWM的情况。1760年L.Euler给出了3D的波方程

(5)

f(x，y，z，t)=F(x，y，z，t)ejωt

式中ω是角频率：代入到Euler的3D波方程，可得标量Helmholtz方程

▽2F+ω2F=0

(6)

这时Maxwell方程组还未出现。当然，电磁学的长久发展和进步的结果便是J.Maxwell于1865年提出电磁场方程组，并逻辑地推出了电磁波的波方程，其现代写法为

(7)

式中Ψ可为电场强度或磁场强度，而Ψ=Ψ(x，y，z，t)；这与Euler的3D波方程是相同的。所以，波方程的微分形式既简单，又概括了力学、声学、电磁学这些领域的波动，显然也可以用到光学。至此，人们的认识水平已大大高于Newton时代。

Maxwell的电磁波方程可简记为MWE，可以把它与SE作比较。公式(4)可写作：

(4a)

而公式(7)可写作：

(7a)

可见，以上两式最大的不同处在于：SE有粒子质量m，而MWE没有。在J.Maxwell做研究的时候并没有光子(photons)的概念；因此他不是认定电磁波与光子对应，而光子的静止质量为零，只是在推导中根本没有(场与波的)质量参数的出现，因为对场与波实在无法谈论质量。

3 不应把光子看成点粒子

所谓点粒子(dot particle)指的是这样的粒子，它没有几何尺寸和体积，也没有质量，实际上只是一个数学点。现有教科书中虽然没有这样说光子，但在实际上都把狭义相对论(SR)作为基础物理理论，而当SR用在光子身上时就必然出现“光子是点粒子”的结果。在SR中有运动体长度缩短公式[7]：

(8)

式中v是运动速度，l0是静止时物体沿运动方向的长度，c是光速。对光子而言v=c，故l=0；因此Einstein光子无体积(尺缩到零，成为一个点)。光子作为一种有动质量、动量、能量的粒子，却无体积，这一观点意味着在SR中光子是点粒子。

其次，粒子物理学通常假定Lorentz—Einstein质速公式为真：

(9)

式中v是粒子速度，c是光速，m0是v=0时的静止质量(rest mass)。物理学教科书从未说过上式不适用于光子，因此人们不妨一试；取m0=0、v=c，则有m=0/0；m成为任意大小，是不可接受的。问题只能出在以下三方面：①质速公式不对；②光子静质量不是零；③光子运动速度不是光速c。显然这三者任何一个成立都与SR不符；实际上，Einstein用自己的SR理论却解释不了自己发现的粒子(光子)。

我们人类天天、时时身处光子的海洋中，而光子的形象竟然是不知形状、无尺寸(无体积)、无质量的东西，这太荒唐了！物理学的发展史曾提供过把电子当作点粒子时的教训。众所周知，量子场论(QFT)和量子电动力学(QED)被认为是很有成就的学科；然而QFT和QED的短板是著名的发散问题，根源在于这是一种点粒子场论。梁昌洪[8]在对经典场(静电场)的自作用能问题作论述时指出，早在1940年R.Feynman就注意到“电子自作用能无限大”给电磁场理论造成了突出的问题，而这是由于描述电子的模型是点粒子。这就是说，点电荷的自作用存在发散困难。如把电子看成没有结构的点，它产生的场对本身作用引起的电磁质量就是无限大。……1964年P.Dirac[9]关于QED的演讲中谈到重整化，他首先论述的正是这个电子质量问题。电子质量当然不会是无限大，不过电子与场相互作用的这个质量会有变化；Dirac指出，无法对“无限大质量”赋于什么意义。人们在“去掉无限大项”的情况下继续计算，得到的结果(如Lamb shift和反常磁矩)都与观测相符；因此就说“QED是个好理论”，不必为它操心了。Dirac对此极为不满，因为所谓“好理论”是在忽略一些无限大时获得的——这既武断也不合理。Dirac说，合理的数学允许忽略小量，却不允许略去无限大(只是因为你不想要它)。……总之，Dirac认为QFT的成功“极为有限”。

尽管光子与电子不同，但把它当作点粒子总归缺乏合理性。必须指出，运动中的光子具有确定的能量E和动质量m：

E=hf

(10)

(11)

因而光子有确定的动量：

(12)

这些基本特性的事实，虽然不证明光子是物质粒子(如同电子)；但我们却不能说：“光(光子)不是物质”。因此，必须抛弃把光子当成点粒子的观点和处理方法。

4 Maxwell电磁理论与Proca重光子理论的比较

Maxwell电磁理论在工程技术中有非常广泛的应用，而且卓有成效。这一事实却使许多人把该理论理想化，认为是绝对正确的东西。但是，光子学说的提出，正是因为Maxwell电磁理论解释不了光电效应。既如此，有什么理由把Maxwell电磁理论理想化呢？1936年A.Proca[10]提出新的电磁场方程组是合乎逻辑的结果；Proca假定对光子而言静质量m0≠0；因此Proca理论又称为重光子理论。本文着重论述这个问题；并且，我们将推导出一组新的电磁波方程，即Proca波方程。这工作本应由A.Proca自己完成，但不知为什么他并没有做。现在笔者就来做这件事，并期待引起专家学者们的注意。

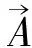
(13)

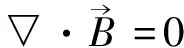
(14)

(15)

(16)

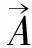
(17)

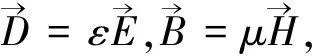
(13a)

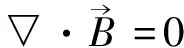
(14a)

(15a)

(16a)

如果光子无静质量(m0=0)，则立即得到人们熟悉的Maxwell方程组。另外还可以证明，在使用Proca方程组的情况下，电磁波的相速、群速为

(18)

(19)

令

(20)

ωc称为截止角频率，故得

(18a)

(19a)

因此，即使是在真空条件下vp、vg也与ω有关，呈现真空中电磁波速的色散效应；只有ω→∞时，真空中相速、群速才与c取得一致。显然，“真空中光速不变”的原理已失去意义。

以上讨论使我们得到下述结论：①Proca电磁场方程组并不是对Maxwell方程组的全盘否定，而是前者比后者更全面。或者说，Proca方程组的出现揭示了Maxwell方程组的近似性。②光子静止质量不为零的理论是与狭义相对论(SR)不相容的物理理论。③Proca理论与量子电动力学(QED)却保持一致；这证明了笔者一直持有的观点，即量子理论与相对论在根本上不相容。

表1给出了两大理论体系的比较；其中的本质性评价为笔者的个人观点，仅供参考。

表1 两大理论体系之比较

5 Proca电磁波方程的推导

怎样认识光子与电磁波的关系？这问题看来简单，实际上并不容易回答。笔者的审慎态度是这样表述的——通常认为光子对应的波动为电磁波；但如认定光子是微观粒子的一种，则它应当有几率波性质，然而现时并没有光子的几率波方程；与此相联系，难于为光子定义波函数。

那么该如何看待光子的波函数(wave function)和波方程(wave equation)？笔者的回答是——有一种看法认为自由态光子的波函数就是电磁平面波函数；与此相应，认为Maxwell电磁波方程就是自由态光子的波方程。但这仅为一种简单化的看法，并未提供呈现光子物理形象的动力学。光子波方程的问题仍需研究。

本文前面已给出公式(7a)，并说它是MWE，即Maxwell波方程。那么，是否应该有与此对应的PWE，即Proca波方程呢？回答是肯定的。但不知为什么，A.Proca本人未作推导，也就没有这样的一份理论遗产。笔者有兴趣于此，做了此事，在本文中介绍出来(并作为文章的重点)。……前面已给出由式(13)、(14)、(15)、(16)组成的Proca方程组，对(16)式两边取旋度，可得

把(15)式代入，有

也就是

亦即

(21)

(22)

等式左方比经典电磁波方程多了一项。

然而

把(16)式代入

故得

也就是

亦即

由(14)式，得到

(23)

(24)

亦即

(24a)

这个PWE也是比经典电磁波方程在等式左端多了一项。(22)式及(24a)式组成完整的PWE，但从表面上看二者不能合为统一的表达形式。总的讲PWE的解与κ有关(也就是与光子静质量m0有关)，这是与经典电磁波方程[公式(7a)]在本质上不同之处。然而这一组PWE和SE[公式(4a)]并列，前者和SE一样在方程中包含了质量参数；这也表示不再无视电磁波的物质性。

6 结束语

光子可能有静质量，其值虽微小却不应忽略。在采用Proca方程组以代替Maxwell方程组的情况下，本文导出了一组新的电磁波方程，即PWE。公式(22)及(24a)是本文的主要结果，它们填补了现有知识的一项空白。如何完善及应用这一组方程，尚待进一步研究。