基于电动汽车充放电的Prosumer单元并网优化研究

程韧俐，王颖，刘东洋，程维杰，马伟哲，翁毅选，马刚

(1. 深圳供电局有限公司，广东 深圳 518001；2.南京师范大学，江苏 南京 210023；3.国电南瑞科技股份有限公司，江苏 南京 211106)

近年来环境污染与能源危机日益加剧，开展节能环保刻不容缓[1-3]。在各大汽车企业、各国政府与科研机构的共同努力下，电动汽车充放电技术与电池技术得到了快速发展。电动汽车逐渐取代燃油汽车，受到了人们的广泛关注，成为众多家庭出行的代步工具[4-7]。

新能源电源与负荷逐步渗入家庭用电单元中，使得家庭能源管理变得更为复杂，既是电能消费者又是电能生产者的这类家庭单元称为“Prosumer”[8]。目前国内外已有众多学者对Prosumer的负荷模型与能量管理等展开研究。在Prosumer单元负荷建模方面，J Munkhammar[9]以伦敦威斯敏斯特市为例，分别对家庭用电量、电动汽车家庭充电与光伏发电量建模，分析家庭负荷用电、电动汽车家庭充电与分布式光伏发电相结合的整个家庭一年四季的用电情况；J Munkhammar[10]针对用户光伏发电和家庭电力消耗在昼夜和季节上的不匹配问题，利用卷积方法将3个独立的现有概率分布模型合并，并提出一个结合家庭用电量、电动汽车家庭充电和光伏发电的模型。在Prosumer单元能量管理方面，M. H Nazari[11]在Prosumer概念的基础上，提出一种电能系统的分布式频率调节框架，但未考虑电动汽车家庭充电情况。在家庭能量管理策略方面，姚钢[12]以住户用能费用最少为目标，利用二进制粒子群优化(particle swarm optimization,PSO)算法进行求解，但并未研究将其接入Prosumer单元中的能量管理策略；李中伟[13]为实现家庭能量管理系统的经济运行、提高用户能量收益和减少用户用能成本，提出一种基于实时电价和NSGA-Ⅱ算法的家庭能量管理系统多目标能量调度优化策略，但NSGA-Ⅱ算法操作较为复杂，影响到家庭能量管理的效率；王珑[14]提出一种基于用户满意度的光蓄互补型家庭能量管理的协调优化调度策略，但并未加入算法对控制策略进行优化。

在上述研究的基础上，本文考虑电动汽车接入Prosumer单元充放电，提出一种Prosumer单元的并网优化方法。首先分析深圳配电网负荷分类及其构成，并根据其特性建立深圳配电网负荷模型；其次，基于电动汽车充放电技术，建立电动汽车充放电模型，并充分考虑其特性，建立Prosumer单元负荷模型；接着，基于改进粒子群优化(modified particle swarm optimization，MPSO)算法，对多个Prosumer单元接入配电网能量进行优化管理，使配电网负荷波动最小化；最后，利用IEEE 33节点配电网模型，对本文提出的多个Prosumer单元并网优化方法进行验证。

1 深圳配电网负荷特性

深圳电网负荷以工业和商业为主，即负荷节点的性质受工业和商业负荷影响比较大，而受农业负荷影响相对较小。本文将深圳市电网负荷划分为工业负荷、商业负荷、居民负荷、其他负荷4个类别，其中其他负荷为包含机构、中小学等除工业、商业和居民负荷以外的负荷类别[15]。

根据深圳2012年夏季最高负荷时刻的负荷数据，以红岭变电站为例，其负荷由各个分类负荷累加而成，合计24 963 kW。其中：工业负荷类用户共1户，平均负荷128 kW，占比0.51%；商业负荷用户共34户，平均负荷累计9 672 kW，占比38.75%；居民负荷类用户共11户，平均负荷累计2 903 kW；其他负荷类用户42户，平均负荷累计12 260 kW，占比49.11%[16]。

可见，深圳市电网负荷受商业影响较大，但商业负荷与工业负荷均属于重要负荷，负荷控制较为困难，若大规模参与日常配电网负荷调控，可能会造成一定经济损失。因此，相比较而言，居民负荷所占比例较高且可控性较强，选择一定比例的居民负荷参与到配电网的负荷调控中具有实际意义。

2 基于电动汽车充放电的Prosumer单元负荷模型

以深圳市负荷特性为例，使居民负荷参与到配电网的负荷调控中，以缓解配电网负荷峰谷差问题，需要对居民负荷进行建模。目前电动汽车逐渐取代了燃油汽车，成为众多家庭出行的选择；因此，本文首先对电动汽车家庭充电模型进行建模，将其充放电特性纳入Prosumer单元负荷模型中，结合家庭日常用电负荷模型，搭建Prosumer单元的负荷模型。

2.1 电动汽车充电负荷模型

电动汽车充电负荷受多方面因素的影响，主要有电动汽车充电模式、充电时间、用户行为习惯、电池特性等。电动汽车的充电时长、用户行为习惯等因素均是随机变量，在时间、空间上都存在不确定性，因此，无法用确定性的方法对电动汽车家庭充电负荷进行计算分析[17]。

快速充电在10～15 min内使电动汽车电量超过80%，充电功率能高达100 kW，其充电站一般建设在公共场所，如大面积的泊车场、酒店、购物商场等停车时间较短的地方，不适用于Prosumer单元[18]；因此，本文考虑电动汽车接入Prosumer单元中充放电时，选择电动汽车慢充电模式。

依据美国家用车辆调查(National Household Travel Survey，NHTS)的统计数据可知[19]，电动汽车的日行驶里程r和起始时间tstart基本符合正态分布，其概率密度函数fD(r)、fs(tstart)分别为：

(1)

(2)

式(1)—(2)中：x为概率密度函数中的tstart变量；μD、σD均为里程系数，分别取值3.2、0.88；μs、σs均为时间系数，分别取值17.6、3.4。

利用蒙特卡洛仿真法模拟家庭电动汽车1 d(24 h)内的充电负荷曲线，如图1所示。

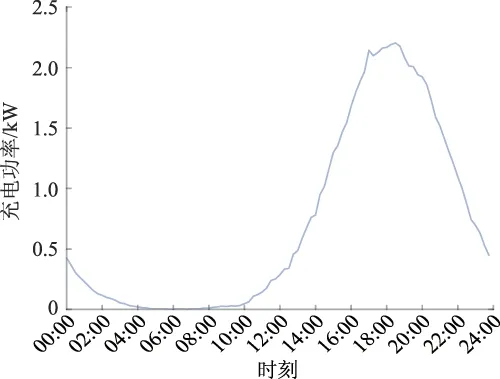
图1 家庭电动汽车充电日负荷曲线Fig.1 Daily charging daily load curve of household electric vehicle

2.2 Prosumer单元负荷模型

电动汽车作为分布式能源，可接入Prosumer单元中充放电，且具有即插即用的功能。结合电动汽车家庭充电模型与家庭用电日负荷模型，建立Prosumer单元日负荷模型。

家庭用电同样具有随机性，目前一般用Weibull分布和对数正态分布来模拟家庭用电[10]，本文通过Weibull概率密度函数对家庭用电建模。Weibull函数利用最大似然法对每小时、每天、每周、每年的数据类别进行估计，结果一共有24×7×12=2 016个分布[20]。家庭日负荷概率模型如图2所示。

图2 家庭日负荷概率模型Fig.2 Household daily load probability model

将电动汽车接入家庭中充放电，结合家庭用电模型，建立以家庭为单位的Prosumer单元负荷模型为

PP(T)=PH(T)+PEV(T).

(3)

式中：PP(T)为Prosumer单元的实时功率；PH(T)为Prosumer单元中家庭负荷的实时功率；PEV(T)为Prosumer单元中电动汽车充电的实时功率。

电动汽车可在电能充裕且无外出需求的情况下向Prosumer单元放电。若PEV符号为正，电动汽车处于充电状态；若PEV符号为负，则电动汽车处于放电状态。若仅允许电动汽车接入Prosumer单元无序充电，Prosumer单元的日负荷模型如图3所示。

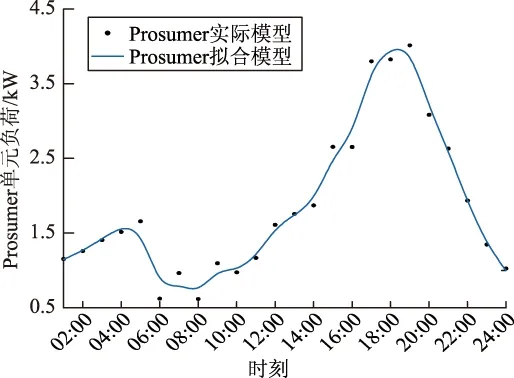
图3 Prosumer单元的日负荷模型Fig.3 Daily load model of Prosumer

当电动汽车接入Prosumer单元无序充电时，其充电负荷会使得Prosumer单元日负荷波动增大，同时增大了Prosumer单元的峰谷差。可见，当电动汽车接入Prosumer单元后，会使大量Prosumer单元日负荷波动叠加，导致配电网日负荷波动加剧，即增大了配电网的峰谷差；因此，Prosumer单元中应利用电动汽车有序的充放电行为，来缓解大量Prosumer单元并网时对配电网负荷波动及网损的影响。

3 基于MPSO算法的Prosumer单元并网优化

本文应用MPSO算法来计算在满足电动汽车需求的前提下，电动汽车接入Prosumer单元中1 d(24 h)内的实时充放电功率最优解。

3.1 约束条件及目标函数

本文利用电动汽车充放电参与配电网负荷调控，求解1 d(24 h)内电动汽车实时充放电功率PEV(T)，使得Prosumer单元日负荷波动最小。因此，目标函数为

(4)

搜索空间中的任意一个位置可表示为

x=(m1,m2,m3,…,mn).

(5)

式中mi为电动汽车在第i时间的充放电功率。搜索空间中的任何一个位置都对应着一种可能存在的求解结果。

由于是对电动汽车充放电行为进行优化，电动汽车的电池对功率有一定承受度，且电池容量也存在着容许范围；因此，根据电动汽车电池容量，设定其容许功率值，即约束条件为：

(6)

式中：PEVd_min与PEVc_max分别为电动汽车放电功率的最小值及电动汽车充电功率的最大值；Smin、Smax为电动汽车电池荷电状态所能容许保存的最小值与最大值。

3.2 优化模型

假设具有j个粒子的种群在n维搜索空间中进行搜索，粒子i在第t次迭代时的起始位置为

xi=(xi_1(t),xi_2(t),xi_3(t),…,xi_n(t)).

(7)

相应的速度为

vi=(vi_1(t),vi_2(t),vi_3(t),…,vi_n(t)).

(8)

其中各维度分量均满足

vmin≤vi_d(t)≤vmax.

(9)

式中：vi_d(t)为第i个粒子在第t次迭代时的第d维度速度分量；vmin、vmax为粒子迭代速度分量的最小值与最大值。

设个体最优位置pi_best(t)表示第i个粒子在第t次迭代时的历史轨迹中优化目标f最小的位置，全局最优位置pg_best(t)表示种群中所有粒子在第t次迭代时的历史轨迹中优化目标f最小的位置，则第i个粒子在第(t+1)次迭代时的速度更新公式为[21]

vi(t+1)=wvi(t)+c1r1(pi_best(t)-

xi(t))+c2r2(pg_best(t)-xi(t)).

(10)

式中：w为惯性权重；c1为跟踪自身最优位置的权重；c2为跟踪全局最优位置的权重；r1与r2为0～1之间服从均匀分布的随机数。第i个粒子在第(t+1)次迭代时的位置更新公式为[22]

xi(t+1)=xi(t)+kvi(t+1).

(11)

式中k为位置更新的约束因子。

根据经验，传统的PSO算法中参数的取值见表1。

表1 PSO算法参数取值Tab.1 Parameter values of PSO algorithm

在传统的PSO算法中，除了r1与r2以外的参数均是静态的，如果粒子经历过的最好位置pbest和种群经历过的最好位置gbest将当前粒子引导到不同的方向，这个粒子将在可行空间中波动。另一方面，如果pbest和gbest与当前粒子的方向相同，粒子将遵循相同的进化方向。在这种情况下，如果gbest距离全局最优点很远，粒子就无法摆脱局部最优点。为了克服传统PSO算法存在的缺陷，本文采用了MPSO算法，其本质在于动态的改变PSO算法中的参数，即：

(12)

MPSO算法中引入了变异操作。为了不让粒子陷入局部最优的困境，引入另一个最优粒子来激励粒子，从而保证在优化过程中粒子能够走向不同的方向，使得粒子跳出局部最优进而探索全局最优位置[23]。

本文提出的基于MPSO算法的Prosumer并网优化算法的基本流程如图4所示。

4 仿真验证

采用IEEE 33节点配电网模型(图5)，结合深圳地区配电网负荷特性，对本文提出的基于电动汽车充放电的Prosumer单元并网优化方法进行验证。

4.1 Prosumer单元优化结果

分别利用传统PSO算法和MPSO算法对Prosumer单元中电动汽车充电情况进行优化，每个优化算法随机进行50次，记录优化目标的平均值、最小值、最大值与标准差，见表2。

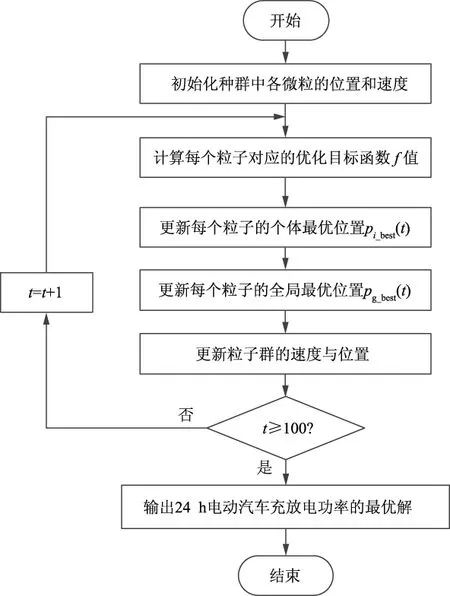
图4 基于MPSO算法的Prosumer并网优化流程Fig.4 Prosumer grid-connected optimization flow chart based on MPSO algorithm

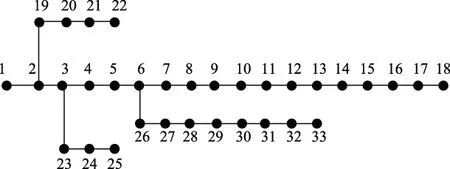
图5 IEEE 33节点配电网拓扑模型Fig.5 Topology model of IEEE 33 node distribution network

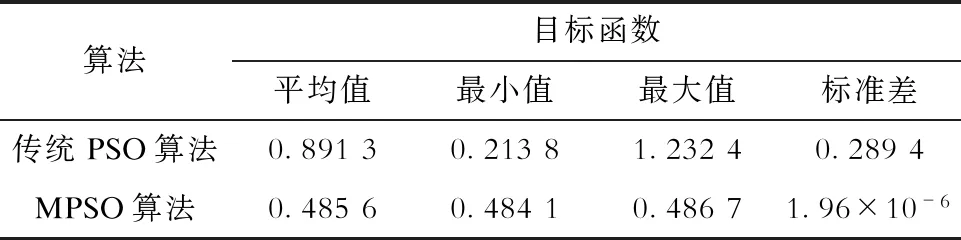
表2 传统PSO算法与MPSO算法对比Tab.2 The comparison between traditional PSO and MPSO algorithm

由表2可见，与传统的PSO算法相比，MPSO算法性能有了较大的提高，经过50次随机优化仿真后，标准差仅1.96×10-6。

利用MPSO算法，对基于电动汽车充放电的Prosumer单元功率负荷模型进行优化，在电动汽车充放电功率范围与电池容量限制的前提下，使Prosumer单元日负荷波动最小。

将未优化的Prosumer负荷与经MPSO算法优化后的Prosumer负荷对比，如图6所示。

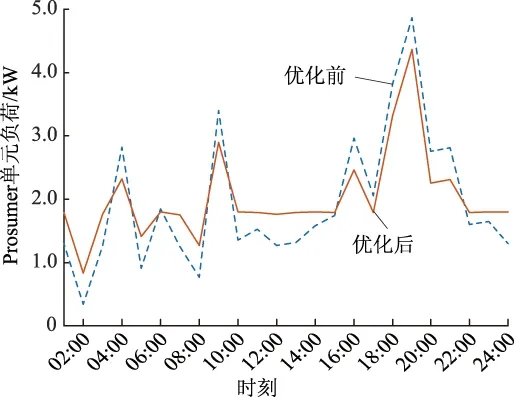
图6 Prosumer单元优化前后负荷对比Fig.6 Comparison of load before and after optimization of Prosumer

经MPSO算法优化电动汽车在Prosumer单元中的充放电行为之后，Prosumer单元的日负荷波动略有下降，由优化前的1.083 1 kW下降到0.485 7 kW，降幅55.16%。可以看出，Prosumer单元在16：00—22：00时段的负荷有明显下降，22：00—06：00(次日)时段的负荷略有上升，即将电动汽车充电时间从负荷高峰期转移至负荷低谷时间段，使得Prosumer单元的日负荷有明显下降，起到了在Prosumer单元中削峰填谷的作用。

4.2 Prosumer单元接入配电网的影响

为研究Prosumer单元接入配电网对配电网电压的影响，选取IEEE 33节点配电网模型，将优化前与优化后的Prosumer单元接入节点5，分析其接入后对配电网节点电压与配电网网损的影响。

Prosumer单元优化前后接入配电网的节点电压对比如图7所示。可以看出优化后的节点电压更为平稳，尽管在00：00—07：00和10：00—14：00时段优化后的节点电压更低，但在配电网负荷高峰期的18：00—22：00时段，配电网节点电压明显提高，电压波动明显减小。

将优化前后的Prosumer单元接入节点5，配电网网损数据见表3。可以看出，配电网网损的变化趋势与Prosumer负荷变化趋势强相关。

由表3可见，经过本文方法优化后，将配电网负荷峰时段的负荷压力转移到平时段与谷时段，降低了配电网负荷的峰谷差，因此在平时段与谷时段，配电网网损略有升高。关键在于经优化的Prosumer单元接入配电网后，在配电网负荷峰时段的网损降幅较大，基本均降低了10%～12%。

图7 配电网节点电压对比Fig.7 Comparison of node voltages before and after Prosumer unit accessing distribution network

表3 配电网网损对比Tab.3 Comparison of distribution network loss

注：时段1为00：00—01：00，以此类推。

综合分析图7与表3可知：Prosumer单元接入配电网后，在负荷高峰期利用电动汽车V2G技术在Prosumer中对负荷和功率的调控作用，降低了Prosumer单元的峰谷差，从而减小了配电网的峰谷差，有效降低了配电网负荷高峰期时的电压偏移和网损。

5 结束语

本文提出了一种基于电动汽车充放电的Prosumer单元并网优化模型。在充分考虑深圳地区负荷特性的基础上，结合电动汽车充放电技术，建立了Prosumer单元的日负荷模型，利用MPSO算法，对Prosumer单元并网能量流通进行优化。电动汽车通过在家庭Prosumer单元中的充放电行为，参与配电网负荷调控。仿真结果验证了该方法可减小Prosumer单元负荷的峰谷差，间接缓解了深圳地区配电网负荷峰谷差问题，在负荷高峰时间段减小了配电网节点电压偏移，也降低了配电网的总网损，具有一定实际意义。