TiO2掺杂粒度对纤维素强度和热稳定性影响的分子模拟研究

王成江，刘玉斌，梅侣松，赵一帆，李亚莎

(三峡大学 电气与新能源学院，宜昌443002)

1 引 言

电力变压器是电力系统中最核心的电气设备，在电能的传输过程中起着至关重要的作用，变压器绝缘纸的主要成分是纤维素，其具有较高绝缘要求. 廖瑞金、吕程等[1, 2]通过真空浸油测试实验研究了纳米TiO2掺杂绝缘纸的绝缘性能，研究表明纳米TiO2掺杂绝缘纸的工频击穿场强有所提高，相比于未掺杂的绝缘纸提高了20.83%. 绝缘性能不仅由电学性能决定，材料的强度和热稳定性也影响着绝缘纸的绝缘性能. 在很多情况下，绝缘失效是由材料的强度和热学及环境造成的[3]. 为了保证电力系统安全稳定运行，提高变压器绝缘纸的强度和热稳定性具有十分重要的意义.

近年来，分子模拟方法已广泛应用到变压器绝缘性能研究[4]，Tang和Zhang等人[5, 6]利用纳米SiO2、Al2O3掺杂纤维素，通过分子模拟研究SiO2和Al2O3掺杂纤维素的力学性能和兼容性等方面，从微观角度阐述纳米SiO2和Al2O3粒子对纤维素掺杂的作用机理.

纳米掺杂聚合物使得形成多界面复合体系，当掺杂颗粒的粒度降低到纳米尺度，聚合物/纳米颗粒的相关特性有全面的提升. 孙伟峰和王暄[7]利用分子模拟研究PI/Cu纳米颗粒复合物的热力学性质和力学特性，研究发现PI/Cu纳米颗粒复合物的热力学性质表现出显著的粒度效应. 谢惊宇[8]利用不同半径SiO2粒子对间位芳纶力学性能和热稳定性进行研究，纳米SiO2与间位芳纶纤维素间的结合能随纳米粒度的增加而增大；间位芳纶纤维素的强度和热稳定性随着纳米SiO2粒度不同表现出明显的粒度效应.

目前，不同纳米TiO2掺杂粒度对纤维素强度和热稳定性影响的研究甚少，本文将采用分子模拟从微观角度分析不同纳米TiO2粒度对纤维素的影响，探索纳米TiO2掺杂粒度对纤维素强度与热稳定性的提升机理及其变化规律，从而为纳米TiO2掺杂纤维素的制备工艺提供理论支撑.

2 模型的建立及仿真细节

2.1 模型的建立

绝缘纸的主要成分为纤维素，其主要有晶体区和无定型区两种存在形式，由于纤维素晶体区相对于无定形区比较稳定不易受到损坏，故利用不同纳米TiO2粒度掺杂纤维素时优先考虑无定型区. 纤维素的重复单元为葡萄糖二糖，纤维素的分子链结构式如图1.

图1 纤维素的分子链结构式Fig. 1 Molecular chain structure of cellulose

Mazcau等[9]发现纤维素链长度在分子构象和理化性质上并没有表现出明显差异，本文由于受到计算机性能的局限，为计算方便，将采用聚合度为10的纤维素进行建模. 利用多尺度建模方法构建未掺杂纳米TiO2和掺杂不同纳米TiO2粒度(2 Å、3 Å、4 Å、5 Å、6 Å、7 Å)的纤维素无定型模型，并保持掺杂体相同的质量分数，即为3%. 通过MS中AC|Packing将聚合度PD=10的纤维素封装为基体，其模型的目标密度均设为1.5 g/cm3[10]，再利用 AC |Calculation将纳米TiO2团簇嵌于基体中间，其构建模型如图2所示.

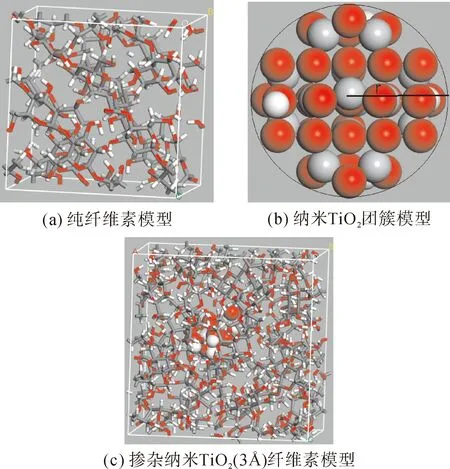
图2 未掺杂纤维素与掺杂纳米TiO2纤维素模型Fig. 2 Undoped cellulose and doped Nano-TiO2 cellulose models

2.2 模拟细节

为了使7组模型能量处于较低状态，先对7组模型分别进行分子动力学弛豫使得体系能量处于较低状态，在此基础上进行目标温度下的分子动力学模拟. 在模拟过程中，考虑到电力变压器常处于正常运行温度和受环境、负载等诸多外界因素影响时局部温度过高，故本文选取的模拟温度为70～150 ℃. 每个体系进行100 ps的平衡模拟，系综设置为NVT，在相同的目标温度下又进行100 ps的分子动力学模拟，系综设置为NPT，待体系达到平衡后，在同样的温度下进行200 ps的分子动力学模拟，系综设置为NPT，积分步长均设置为1 fs，压强设置为0.001 GPa，体系内各原子的动力学信息每隔500 fs收集一次，以用于分析.

整个模拟流程均采用COMPASS力场，此力场已经被证实非常适合计算有机和无机分子构成的体系. 温度控制采用Anderse热浴法，压强控制采用 Berendsen压浴法，并用velocity verlet跳蛙算法进行牛顿运动方程求解. 对于非键相互作用，范德华作用采用Atom Based方法，静电作用采用Ewald法.

3 强度的表征与分析

3.1 强度的表征

纤维素作为电力变压器内部绝缘纸的主要成分，其具有较高的强度. 通常利用拉伸模量(E)、体积模量与剪切模量的比值(K/G)、泊松比(γ)和柯西压(C12-C44)等微观参数表征强度. 由弹性力学可知，固体材料的应力-形变之间的关系可以用广义Hooke定律[11]表示：

式中σ为应力、τ为切应力、ε为应变、γ为切应变. 拉梅系数λ、μ和强度参数均可由以下推到公式得出：

(1)

(2)

(3)

(4)

(5)

G=μ

(6)

强度微观参数的定义：拉伸模量(E)为应力与应变的比值，是度量材料钢性的参数，拉伸模量与材料的钢性成正比，拉伸模量越大，材料的钢性越强；体积模量与剪贴模量的比值(K/G)用于评价材料的韧性，其值越大表明材料的韧性越好；泊松比(γ)为横向应变与纵向应变的比值，反映材料横向变形的弹性常数，其值越大材料的可塑性越强；柯西压(C12-C44)用于衡量材料的延展性，其值越大材料的延展性越强，其值越负材料的脆性越强.

3.2 掺杂纳米TiO2对纤维素强度的影响

图3左坐标表示70 ℃～150 ℃下未掺杂和掺杂纳米TiO2纤维素的拉伸模量变化趋势，纳米TiO2掺杂纤维素的拉伸模量比未掺杂模型整体偏大. 随着温度升高，掺杂TiO2纤维素的拉伸模量减小的幅度比未掺杂纳米小，可见，纳米TiO2掺杂纤维素使得拉伸模量随温度的升高而减少的幅度较小，纳米TiO2使得纤维素形变难度加大，抗形变能力加强. 图3右边的坐标轴为K/G，掺杂和未掺杂TiO2纤维素均表现出相同的变化趋势，即先增大后减小再增大，在90 ℃和130 ℃时达到最大. 从整体图形看，纳米TiO2掺杂纤维素的K/G均比未掺杂的值大. 掺杂纳米TiO2使得纤维素韧性有较大的提升. 综上微观强度参数对比分析，掺杂纳米TiO2使得纤维素的强度得到提升.

图3 未掺杂、掺杂模型的拉伸模量、K/G值Fig. 3 Tensile modulus and K/G values of undoped and doped models

3.3 纳米TiO2掺杂粒度对纤维素强度的影响

考虑到纳米TiO2对纤维素的强度影响，掺杂不同纳米TiO2粒度对纤维素的拉伸模量、泊松比和柯西压等微观参数进行分析. 图4表示掺杂不同纳米TiO2粒度纤维素的拉伸模量和泊松比在70 ℃、90 ℃下的变化趋势. 由图可知拉伸模量和泊松比在70 ℃和90 ℃时的变化趋势均相同，即拉伸模量随纳米粒度增加逐渐减小，泊松比随纳米粒度增加逐渐增大. 不同纳米TiO2粒度掺杂纤维素在温度的影响下出现相同的变化趋势，故可以选取一个温度进行不同纳米粒度对纤维素的影响研究.

在70 ℃下，随着纳米TiO2粒度增加，拉伸模量呈减小趋势，纳米TiO2掺杂纤维素的强度逐渐减小，抗形变能力减弱. 随着纳米TiO2粒度增大，纳米TiO2掺杂纤维素的泊松比增大，纤维素的可塑性增强，在外力和应力的作用下容易发生形变，使得材料的钢性减弱，强度降低. 图3可以得出，纳米TiO2掺杂纤维素的拉伸模量和柯西压均出现粒度效应，当纳米TiO2粒度越小，掺杂纳米的纤维素的拉伸模量越大和泊松比越小，抗性变能力越强，材料的强度越好.

图4 不同纳米TiO2粒度的拉伸模量、K/G值Fig. 4 Tensile modulus and K/G values of different Nano-TiO2 granularities

图5为掺杂不同纳米TiO2粒度的纤维素在70 ℃、90 ℃时的柯西压值，随着纳米TiO2粒度增大，纤维素的柯西压值呈减小趋势. 纳米TiO2半径为2.0 Å时，纳米TiO2掺杂纤维素的柯西压最大，其值为3.0 Å左右，当纳米TiO2半径逐渐增加到7.0 Å时，柯西压值随着半径增大逐渐减小，由此证明，掺杂纳米TiO2可以提升纤维素的柯西压值，纳米粒度越小，纤维素的柯西压值越大，材料的延展性越强，材料发生形变而不产生裂纹的能力越强.

图5 不同纳米TiO2粒度的柯西压Fig. 5 Cauchy pressure of different Nano-TiO2 particle sizes

3.4 机理分析

掺杂不同粒度纳米TiO2对纤维素的拉伸模量、泊松比和柯西压均有一定提升，其作用机理：纳米TiO2粒度越小，纳米TiO2越容易分散于纤维素中，小纳米粒度团簇的比表面积大，其表面O与H原子形成的表面羟基易于纤维素形成氢键，使得纳米TiO2与纤维素紧密形成复合体系，基体纤维素受到张力作用，纳米粒子与基体之间会产生银纹，基体纤维素也产生塑性形变，吸收一定的张力，由于无机纳米粒度比较小、比表面积相对较大，纳米TiO2与基体纤维素间接触面也就比较大. 当纤维素受到外来张力时会产生更多银纹及塑性形变，并吸收更多张力从而达到增韧效果. 纳米TiO2与纤维素紧密结合，一部分载荷被纳米TiO2承担，从而使得纤维素的抗张强度增加.

4 热稳定性的表征与分析

4.1 热稳定性的表征

电力变压器长期运行在高温条件下，纤维素作为绝缘纸的主要成分需要具有较高的热稳定性，温度过高会使纤维素发生强烈的链运动，使得结构遭到破坏. 通常利用径向分布函数、自由体积和均方位移表征纤维素的热稳定性.

径向分布函数(RDF)用来分析纤维素间的氢键数目的变化情况，表征纤维素的氢键结合程度. 径向分布函数峰值越大，体系氢键数越多，体系就越稳定，材料的热稳定性越好.

均方位移描述链的整体移动情况，纤维素的链运动很大程度上影响着纤维素的热稳定性. 纤维素的链运动越剧烈，纤维素的热稳定性就越差，其均方位移(MSD)的表达式[12]为：

(7)

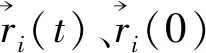
通过Fox和Flory的自体积理论[12]阐述纤维素的热稳定性，其理论：材料的总体积分为两部分，即占有体积(Occupied Volume，VOV)和自由体积(Free Volume,VFV)，占有体积表示该部分被分子占据的体积，自由体积表示为该部分未被占据的体积，也称空隙，则自由体积分数(fFFV)推导公式：

(8)

式中，fFFV为自由体积分数，VFV为自由体积，VOV为占有体积.

自由体积分数为自由体积占总体积的比重，自由体积分数越小，材料的内部空隙就越小，纤维素链在分子层面不容易发生链运动，材料结构相对稳定，受温度的影响较小，热稳定性较强.

4.2 掺杂纳米TiO2对纤维素热稳定性的影响

图6(a)(b)表示未掺杂和掺杂纳米TiO2纤维素的径向分布函数(RDF)，未掺杂和掺杂纳米TiO2纤维素的径向分布函数在0.097 nm附近出现强烈的峰值. 由于径向分布函数的主图线条太密集，故将0.208-0.26 nm的RDF图形放大，如局部图所示，在0.208 nm和0.245 nm附近出现中等强度的峰值，此范围正好处于纤维素中的氧原子与纳米TiO2的表面羟基形成氢键的范围. 图6(a)(b)中的局部图0.208～0.245 nm范围的峰值对比发现纳米TiO2掺杂纤维素在各个温度下的RDF均比未掺杂的纤维素峰值大. 为更清楚地观察掺杂之后的变化情况，本文把70 ℃时未掺杂和掺杂纳米TiO2纤维素的径向分布函数进行对比分析，如图6(c)所示.

(a)未掺杂TiO2纤维素的RDF

(b)掺杂TiO2纤维素的RDF

由图6(c)可知，纳米TiO2掺杂纤维素在0.208 nm和0.245 nm处的RDF峰值均比未掺杂的RDF峰值大，纤维素中H与TiO2中O形成氢键，从而增加纤维素与TiO2复合体系的氢键数目. 由图6(a)(b)可以看出，随着变压器运行温度升高，纤维素在0.2 nm～0.26 nm之间中等强度的峰值趋于减小，90 ℃～150 ℃的RDF均比70 ℃的RDF小. 研究表明纤维素出现链老化趋势，纤维素分子间的氢键数目相对减少. 纳米TiO2掺杂的纤维素同样会随着温度的升高，出现链老化的情况，但由图6(c)的中等强度峰值对比发现，纳米TiO2掺杂纤维素的氢键数目随温度升高减小的程度小于未掺杂纳米TiO2中氢键数目减小的程度.

4.3 纳米TiO2掺杂粒度对纤维素热稳定性的影响

考虑到纳米TiO2对纤维素热稳定性的影响，通过掺杂不同纳米TiO2粒度对纤维素的热稳定性进行分析. 通过Fox和Flory的自体积理论和分子运动理论可知，空隙是材料中微观粒子运动的原因，因此可以用自由体积理论解释绝缘材料的热稳定性. 利用硬球探针法计算自由体积的，纤维素的硬球半径无法获得，在此利用范德华半径为硬球探针. 通过MS软件分析不同粒度的纳米TiO2掺杂纤维素的自由体积，其具体数据如表1.

表1 不同纳米TiO2尺寸掺杂纤维素的自由体积(VFV)、占有体积(VOV)和自由体积分数(FFV)

Table 1 Free volumes, occupying volumes and free volume fractions of celluloses doped with different Nano-TiO2sizes

RVOVVFVFFFV2Å4988.23Å2651.53Å20.1163Å9802.86Å21436.56Å20.1284Å17259.08Å25166.69Å20.1355Å40014.25Å210638.75Å20.2106Å17345.59Å263275.98Å20.2157Å29479.47Å288891.30Å20.249

表1为不同纳米粒度掺杂纤维素的占有体积、自由体积和自由体积分数. 从自由体积分数可以看出，随着纳米TiO2粒度逐渐增大，纤维素的自由体积分数逐渐增大，其模型的自由体积逐渐增大. 小粒度纳米TiO2更容易掺杂到纤维素间隙中，纳米TiO2填补原有的自由体积空隙，从而减小复合体系的自由体积，进而减弱纤维素分子的链运动. 同时纤维素体系中掺杂纳米TiO2打破原有的氢键网络，纳米TiO2表面羟基易于纤维素的羟基之间形成氢键，新的氢键网络使得整个复合体系结构更加紧密，纳米TiO2通过羟基抑制纤维素的链运动，使得复合体系的结构更加稳定，纳米TiO2掺杂纤维素的热稳定性增强.

图7为不同纳米粒度TiO2掺杂纤维素在70℃时的均方位移(MSD). 如图7所示，掺杂不同纳米粒度TiO2使得纤维素的MSD值出现不同的跳变. 掺杂纳米TiO2粒度为2 Å、3 Å、4 Å、5 Å、6 Å、7 Å时，复合体系的MSD分别为3 Å2、10 Å2、11 Å2、20 Å2、27 Å2、34 Å2左右. 由此可以得出，随着纳米TiO2粒度的增加，纳米TiO2掺杂纤维素的MSD逐渐增大，则纤维素的链运动逐渐增加，复合体系的稳定性逐渐变差. 掺杂不同纳米粒度TiO2使得复合体系表现出明显的粒度效应，掺杂纳米TiO2粒度越小，纤维素的链运动越弱，复合体系热稳定性较好.

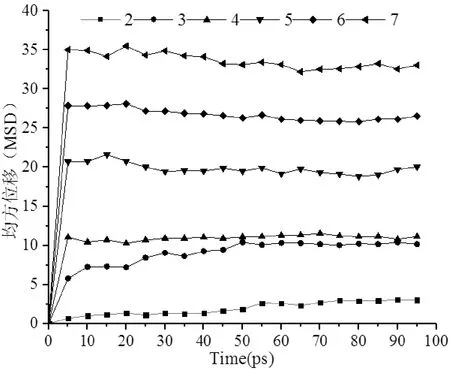
图7 70 ℃时不同纳米TiO2粒度的MSDFig.7 MSDs of different Nano-TiO2 sizes at 70 ℃

4.4 机理分析

为了便于解释纳米TiO2粒度掺杂纤维素的机理，本文引入纳米TiO2粒度表面羟基占有率的概念，其公式：

(9)

式中，PTiO2为纳米TiO2粒度表面羟基占有率，MOH表面羟基原子数，MTiO2团簇总原子数.

表2是不同纳米TiO2粒度表面羟基占有率，通过表2可以看出纳米TiO2粒度越小，纳米TiO2表面羟基占有率越高，小纳米粒度的TiO2表面羟基与纤维素间形成的氢键数目占总体系氢键数目比重较大，纳米TiO2抑制纤维素链运动的强度越大，使得复合体系更加稳定. 从不同纳米粒度的纳米TiO2掺杂纤维素的复合体系的自由体积和表面羟基占有率可以看出，当掺杂比例相同的情况下，纳米TiO2掺杂纤维素表现出明显的粒度效应，纳米粒度越小，纳米TiO2掺杂纤维素的复合体系更加稳定，复合体系的热稳定性更强.

5 结 论

本文通过分子模拟对不同纳米TiO2粒度掺杂纤维素进行模拟研究. 通过模拟结果和数据对比分析，得出以下结论：

表2 不同纳米TiO2粒度表面羟基占有率

Table 2 Hydroxyl shares of different Nano-TiO2particle size surfaces

纳米半径(R)表面处理的TiO2团簇原子数(含氢原子)表面羟基占有率2.0ÅM(H/O/Ti)=6/6/10.463.0ÅM(H/O/Ti)=6/9/30.3304.0ÅM(H/O/Ti)=8/17/70.2505.0ÅM(H/O/Ti)=12/34/180.1886.0ÅM(H/O/Ti)=20/63/250.1857.0ÅM(H/O/Ti)=26/92/380.167

1)掺杂纳米TiO2使得纤维素强度有较好提升，拉伸模量增大，抗形变能力增强，体积模量与剪切模量比值增大，韧性增强；掺杂纳米TiO2使得纤维素稳定性提升，纳米TiO2与纤维素形成的氢键抑制纤维素链运动，使得复合体系的结构稳定、热稳定性增强.

2)随着纳米TiO2粒度逐渐减小，拉伸模量和柯西压呈增大趋势，泊松比逐渐减小，纤维素的强度增大；纳米TiO2的粒度越小，纳米TiO2表面羟基占有率越高，复合体系的自由体积越小，均方位移越小，纤维素链运动越弱，复合体系越稳定，纳米TiO2掺杂纤维素热稳定性越强，故掺杂小纳米粒度TiO2是提升绝缘纸强度和热稳定有效的方法.