一种基于Zieloger-Niclosls法的反应堆堆芯功率PID串级控制器整定方法研究

何伯阳，吴 茜，黄 勇

（中广核研究院有限公司 北京分公司，北京 100086）

0 引言

目前，某型在研实验动力堆采用“折线型”双恒定方案，即高于一定功率时，一回路平均温度恒定、OTSG出口压力恒定的“双恒定”总体控制策略[1]。因而提出了对堆芯平均温度的控制要求。

然而，在该型反应堆实际工作过程中，冷却剂硼浓度波动、温度负反馈和燃料多普勒效应会引起堆芯反应性扰动，从而导致反应堆功率波动[2]。同时，堆芯下腔室冷却剂入口温度、主泵转速变化也会引起反应堆堆芯温度波动[2]。温度波动效应和反应性波动效应叠加，从而影响到“折线型”双恒定方案的实现。因此，为了保障反应堆能按照设定水平输出功率，需要设计一个专用的“温度-功率”控制器，以实现对堆芯温度、功率的控制。

1 堆芯系统开环控制学模型

为了设计该实验动力堆控制系统，需要准确建立被控过程的数学模型，然后依据该模型，按照控制需求来设计控制器。由于目前尚未建立实验堆，不具备实验辨识条件。因此，本文主要采用解析建模法在已有设计参数的基础上建立堆芯系统的模型。

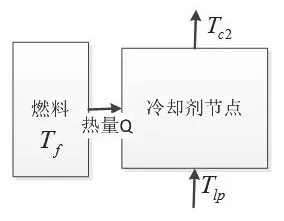
图1 堆芯热工水力学模型Fig.1 Thermo-hydraulic model of core reactor

解析建模法就是针对建模对象，建立各种平衡方程，如：质量守恒方程、能量守恒方程、动量平衡方程，通过微分方程组来描述系统动力学特性，即是系统的状态空间描述。通过线性化状态空间方程，可求得系统的传递函数矩阵。

1.1 堆芯物理模型

在反应堆系统设计中，点堆方程是主要的非线性环节。在稳态工作点邻域内，点堆方程可以线性化，由此建立系统的传递函数。

经典点堆方程如式（1）所示[3]：

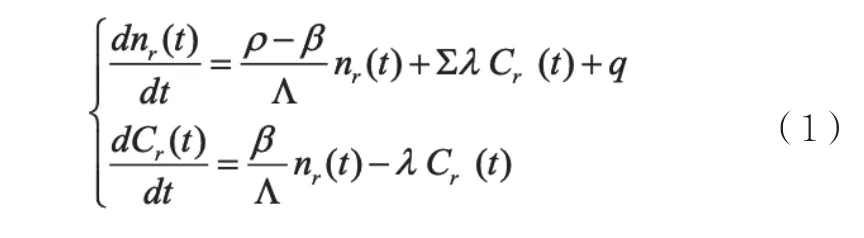
其中：

nr(t) --t时刻的相对中子密度。

Cr(t) --t时刻的缓发中子先驱核相对密度。

ρ(t) --t时刻引入的反应性。

β--缓发中子总份额。

λ--缓发中子衰变常数，s-1。

1.2 堆芯热工水力学模型

堆芯热工动力学模型采用平均通道等效近似来处理，由于堆芯物理模型为点堆方程，不考虑堆芯功率分布。因此，燃料仅采用一个节点；由于采用集总参数法，所以冷却剂则采用单个节点。示意图如图1所示。

其中：

Tf--燃料温度，Co

Tc2--冷却剂节点出口温度，Co

Tlp--冷却剂节点入口温度，Co

Tavg--冷却剂平均温度，Co

1.3 燃料能量守恒方程

堆芯燃料的热量变化率等于燃料产热功率减去燃料传递给冷却剂节点的热功率，即如式（2）所示：

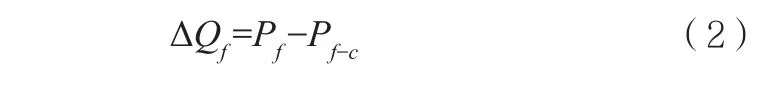
其中：ΔQf表示堆芯燃料的热量变化率，Pf表示燃料产热功率，Pf-c表示燃料传递给冷却剂节点的热功率。又因为燃料热量变化率与燃料温度变化率成以下关系：

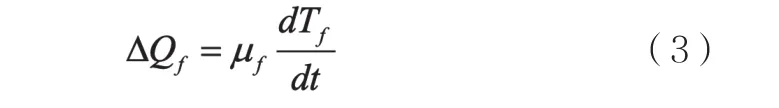
假设燃料中产生热量占总功率的份额为f，则燃料产热功率如下：

其中，PFLL表示实际功率，P0表示反应堆满功率值，nr表示相对中子密度。

又由于传热公式可得：

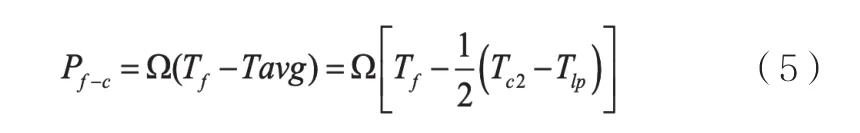
将式子代入上述方程式（5）可得：

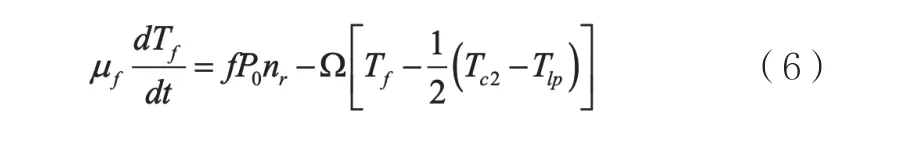
1.4 冷却剂节点能量守恒方程

冷却剂节点热量变化率等于冷却剂中产生的热功率加燃料传递给冷却剂的热功率—冷却剂流动带走的热功率，如下：

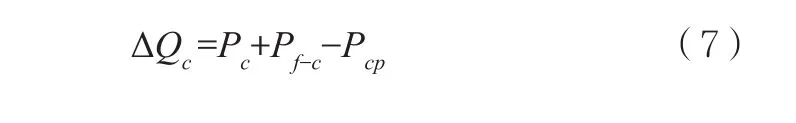
其中：ΔQc表示冷却剂节点热量变化率，Pc表示冷却剂中产生的热功率，Pf-c表示燃料传递给冷却剂的热功率，Pcp表示冷却剂流动带走的热功率。附注：以上过程不考虑热量散失。又因为冷却剂热量变化率与冷却剂温度变化率成以下关系：

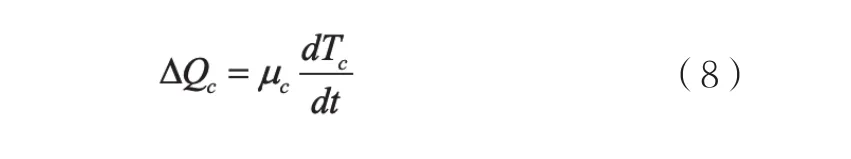
假设燃料中产生热量占总功率的份额为f，则冷却剂产热占总功率的份额为（1-f）。因此，冷却剂产热功率如下：

又由于传热公式可得：

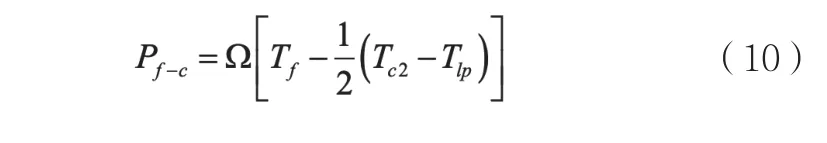
冷却剂流动带走的热功率如下：

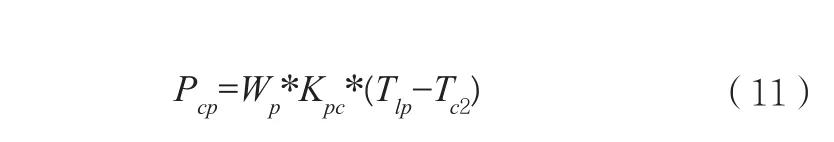
其中：Wp表示冷却剂工质流量，Kpc表示工质热容。可得：

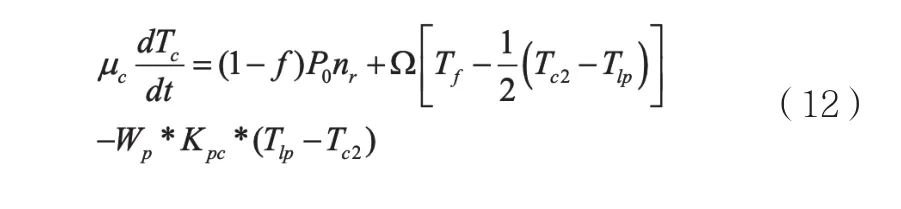
1.5 反应性调节

反应性反馈考虑了燃料与冷却剂温度作用，忽略氙等毒素引入的反应性反馈，即：总反应性等于控制棒引入的反应性减去燃料多普勒效应引入的负反应性减去冷却剂引入的负反应性。

设控制棒引入的反应性为ρrod，燃料多普勒系数为αf，冷却剂负温度系数为αc，则总反应性如下：

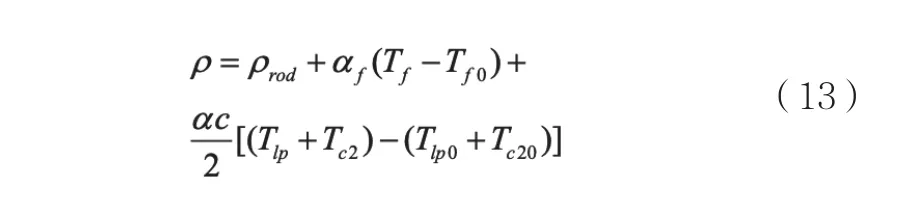
将式（13）反应性负反馈方程代入归一化点堆方程（1）可得：

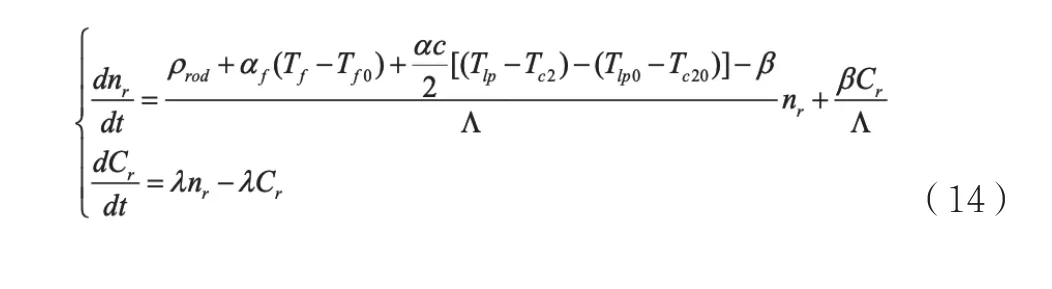
1.6 系统动力学微分方程组

在得到上述方程后，可以整理得到描述系统动力学特性的微分方程组如下：

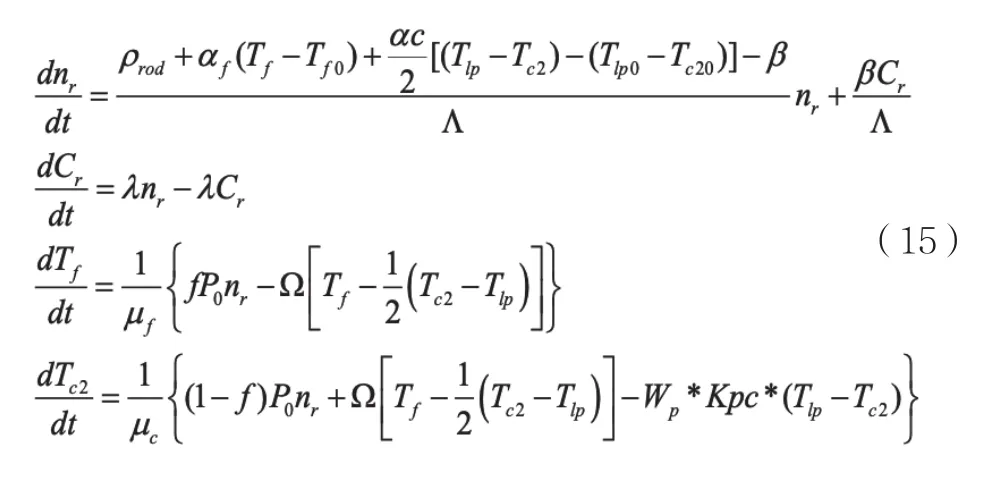
建立系统状态空间表达式主要方法有两种：第一种方法是根据系统的工作原理，选择相关物理量作为系统的状态变量，直接写出状态方程；第二种方法是根据系统的动力学微分方程组，推导出状态方程[4]。本文采用第二种方法。

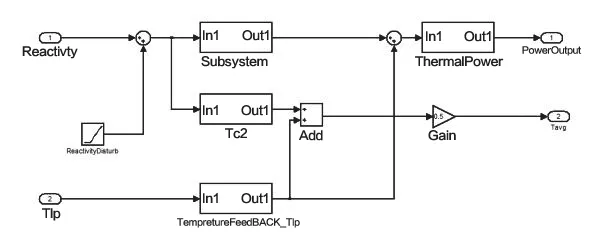
图2 堆芯系统Matlab/Simulink模型Fig.2 Matlab/simulink Model of core system

建立系统的状态空间表达式的第一步是选取状态变量[5]。系统在时域空间中运动信息称为状态，确定系统状态的一组独立变量（数目最小）称为状态变量，它是能够完整、确定的描述系统时域行为的最少的一组变量[6]。在上述微分方程组中，涉及到6个变量：nr，Cr，Tf，Tc2，ρrod，Tlp，其中ρrod，Tlp是人为输入量。因此，仅凭nr，Cr，Tf，Tc2，就可以表征系统的状态。所以选取系统状态变量如下：

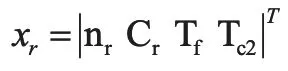
并以

为输入量。将前述微分方程改写为以下形式：

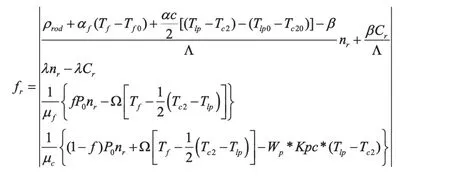
则有系统的状态空间模型如下：

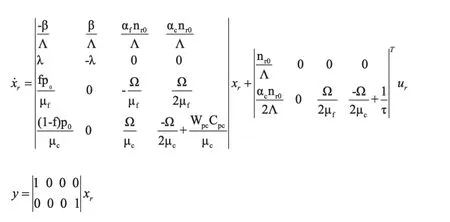
1.7 反应堆控制学模型

根据上述数学模型，结合该型动力实验堆系统设计参数[7]，在Matlab/simulink中搭建系统的开环模型如图2所示。

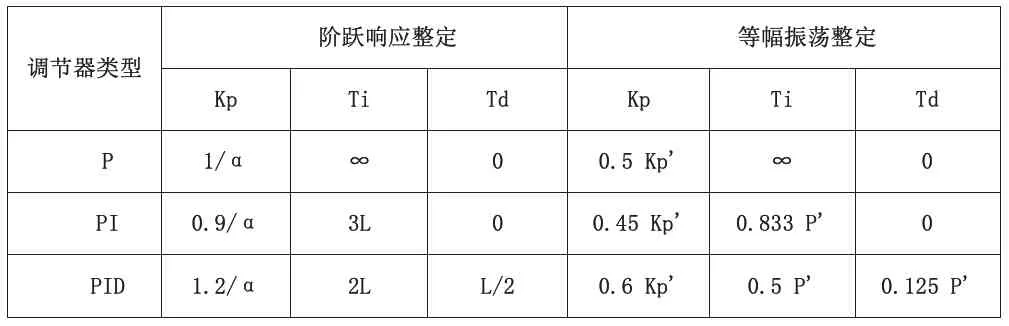
表1 PID控制器的有关参数整定关系表Table 1 Parameter setting relation table for PID controller

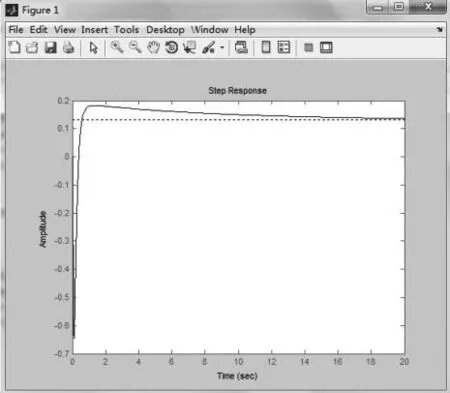
图3 堆芯开环系统阶跃响应曲线Fig.3 Step response curve of core open loop system

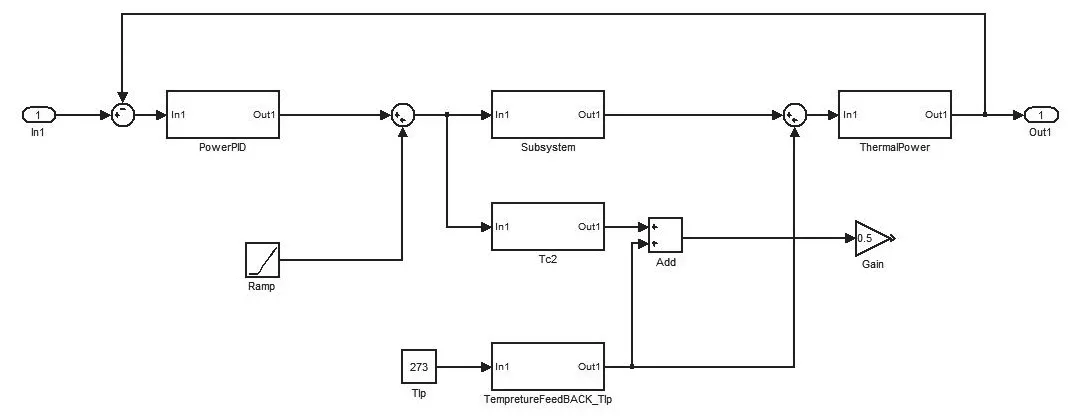
图4 带一级控制器的堆芯Matlab/Simulink模型Fig.4 Core Matlab/simulink model with first-level controller

2 PID 控制器解析化设计方法

PID控制器解析化设计方法的核心是由被控对象的数学模型直接得出PID 控制器的参数[8]。基于不同的控制要求和优化准则有多种设计方法，Zieloger-Niclosls法是一种常用方法[9]。

实现方法：设想对被控对象（开环系统）施加一个阶跃信号，通过实验方法，测出其响应信号。则输出信号可由图中的形状近似确定参数k，L和T（或α，α=kL/T）。如果获得了参数k，L和T（或α）后，则可根据表1确定PID控制器的有关参数[9]。

整定过程如下：

首先，对1.7节中模型施加阶跃信号，获得系统的阶跃响应曲线。该部分用Matlab代码实现，获得阶跃响应曲线如图3所示。从该阶跃响应曲线可以获得3个主要参数k，L和T，并按照表1的关系计算出PID控制器3个整定值Kd，Ki，Kp。

其次，将上述参数填入一级串级控制器，得到系统的功率闭环模型如图4所示。

对上述功率闭环模型再次施加阶跃信号，获得其阶跃响应曲线，观察该曲线参数，确保曲线负荷超调量、调节时间、稳态误差等性能指标符合设计要求[1]。

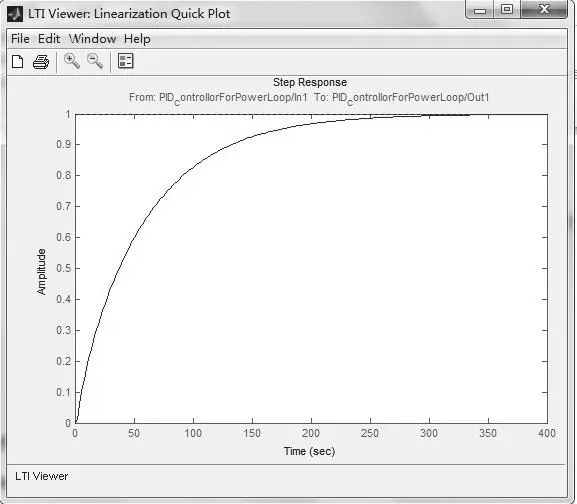
图5 带一级控制器的堆芯模型阶跃响应曲线Fig.5 Step response curve of core model with primary controller

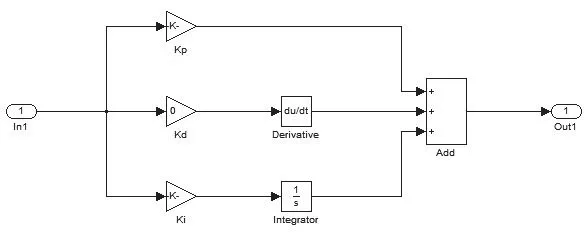
图6 温度闭环PID控制器Fig.6 Temperature closed-loop PID controller

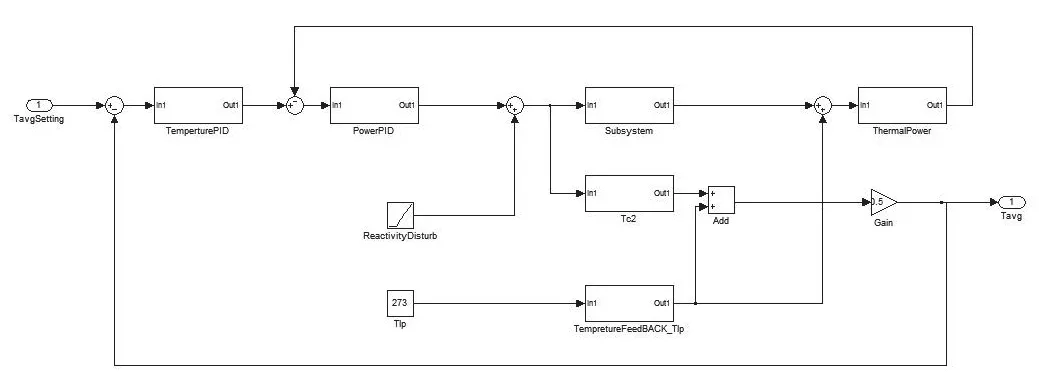
图7 带PI-PID串级控制器的堆芯温度-功率控制系统Fig.7 Core temperature-power control system with PI-PID cascade controller

获得了第一级功率PID控制器后，可以将功率控制器件和开环系统封装为一个子系统，然后再添加一个温度PID控制器，只要整定了温度环PID 3个参数即可以获得系统的PID控制器。由于一回路平均温度受到堆芯入口温度影响，所以波动较为频繁，为了防止控制器频繁动作导致控制性能恶化，温度闭环控制器将微分环节参数取为零。只采用PI控制，具体结构如图6所示。

该环节整定方法和功率整定方法类似，可以直接采用第一个控制器参数范围内取值。令

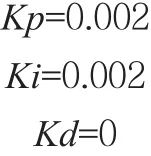
将上述参数填写入控制器中，即得到带参数的温度PID控制器。得到了两个闭环控制器后如图7所示。

3 仿真结果分析

对上述闭环控制系统施加阶跃信号，得到阶跃响应曲线如图8所示。

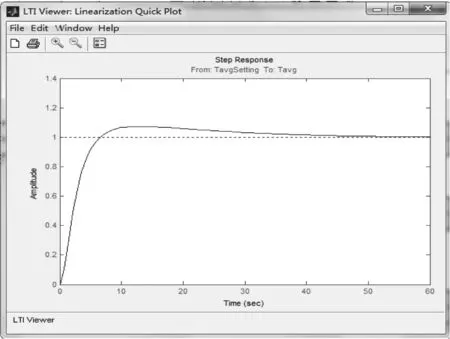
图8 PI-PID串级控制器的堆芯温度-功率控制系统阶跃响应曲线Fig.8 Core temperature-power control system step response curve for PI-PID cascade controller

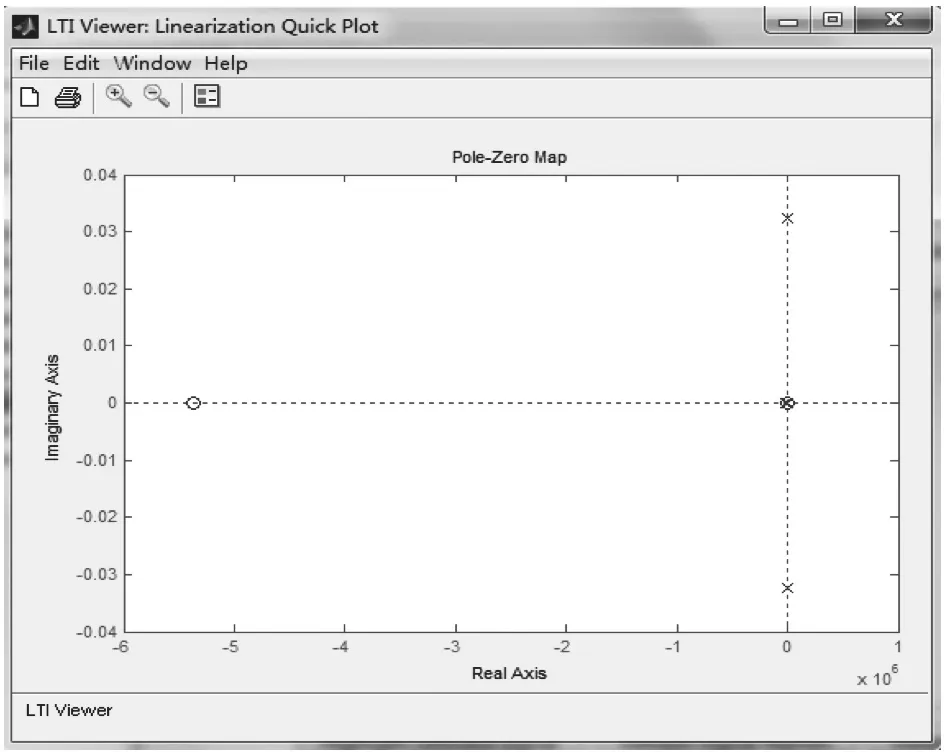
图9 闭环系统零极点分布图Fig.9 Closed-loop system 0 pole distribution

图8阶跃响应曲线，该控制系统可以较好地跟踪阶跃输入信号。稳态误差为零，稳态响应时间为6s～10s，超调量不超过稳态值的10%。因此，认为该控制系统满足控制精度和响应速度的要求[9]。

同时，完成动态特性分析后，利用Matlab/Simulink环境下获得其零极点分布如图9所示。

从图上可以看出，坐标轴右侧没有极点分布。通过经典控制理论判断，该系统不会出现失稳定状态[9]。同时坐标轴上有两个极点，为了进一步提高使用的稳定性，可以再设计校正环节。通过改变系统零极点分布的方式来改善系统的响应特性。