基于叠加柔性铰链的超磁致伸缩驱动器建模与实验
周景涛 何忠波 柏 果 刘国平
(陆军工程大学石家庄校区车辆与电气工程系, 石家庄 050003)
0 引言
超磁致伸缩材料(Giant magnetostrictive material, GMM)具有输出功率大、能量密度高、响应快和滞环低等优点[1-2],逐渐成为当前研究的热点之一。以GMM为核心的致动器[3]输出位移误差在40 nm以内,能实现很高的进给精度。采用GMM驱动技术的高精度定位装置[4],定位精度能够达到±30nm。以GMM为执行元件的主动减振降噪系统[5]具有频带宽、低频特性好的特点,最大减振量可达70%。另外,GMM还广泛应用于开关阀[6]、流量控制阀[7]、高精度传感器[8]和能量收集装置[9]等,实现了良好的控制精度和反应速度。GMM的磁致伸缩系数较小(1×10-3),其输出位移小的缺点使其在工程技术方面的应用受到了一定限制。通过一些液压放大机构或机械放大机构可以在一定程度上放大输出位移[10-12],但同时也成比例地缩小了输出力,降低了系统灵敏度。利用惯性冲击原理研制的惯性-摩擦式驱动器[13-14]可以实现大行程进给和精密定位,但输出力较小。
柔性铰链是依靠本身形变来传输运动或力的运动副,具有无摩擦、无间隙、运动灵敏度高、导向精度高等诸多特点[15],广泛应用在精密机械和仪器等领域。有学者对柔性铰链的力学特性进行了研究[16-17],并通过有限元法[18]进行了预测分析;有些研究利用积分法[19]或奇异函数法[20]得到了在目标方向上的等效刚度,CHOI等[21]利用刚度矩阵法对机构进行了动力学建模,LOBONTIU等[22]推导了用柔度表示柔性铰链的弹性运动方程,宗光华等[23]利用弯曲变形理论建立了柔性铰链平行四杆机构屈曲临界力的数学模型,MA等[24]通过双梁约束模型得到了非线性特性的解析表达式。
本文设计一种基于尺蠖运动方式的高精度、大行程的超磁致伸缩直线驱动器,对叠加式柔性铰链进行受力分析、强度校核和模态分析,建立输出位移模型,并对样机进行实验测试。
1 工作原理
超磁致伸缩直线驱动器仿生“尺蠖”运动形式,主要由驱动机构、前箝位机构、后箝位机构和导轨组成,其工作原理如图1所示,通过以下步骤完成一次步进运动:
(1)后固定:后箝位机构伸长,固定在导轨上。
(2)前解脱:前箝位机构收缩,与导轨解脱。
(3)驱动:驱动机构伸长,推动前箝位机构向前移动。
(4)前固定:前箝位机构伸长,固定在导轨上。
(5)后解脱:后箝位机构收缩,与导轨解脱。
(6)复位:驱动机构收缩,拉动后钳紧机构向前移动。
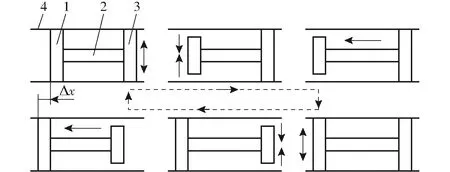
图1 直线驱动器的工作原理Fig.1 Working principle of linear actuator1.前箝位机构 2.驱动机构 3.后箝位机构 4.导轨
以上6个步骤为一个工作周期,系统完成一次“推-拉”动作,输出单步位移Δx。系统不断循环,可实现位移的“尺蠖式”步进输出。理论上,如果导轨足够长,可实现无穷大的位移输出。
2 机构设计
2.1 结构设计
直线型驱动器主要由驱动机构、前箝位机构、后箝位机构、动子和导轨组成,如图2所示。驱动机构、前后箝位机构分别安装在动子的中间和两端,其结构基本相同,主要由GMM棒、轭铁、楔形块、线圈和螺钉组成。动子的多层薄板状结构形成叠加式柔性铰链,线圈通电时,GMM棒伸长,柔性铰链产生形变并储存能量,线圈掉电时,GMM棒收缩,在柔性铰链的弹性作用下,机构回位。转动螺钉,通过楔形块A推动楔形块B产生垂直方向的位移,可以为GMM棒提供较大的预紧力,并能够较准确地控制预紧力的大小。
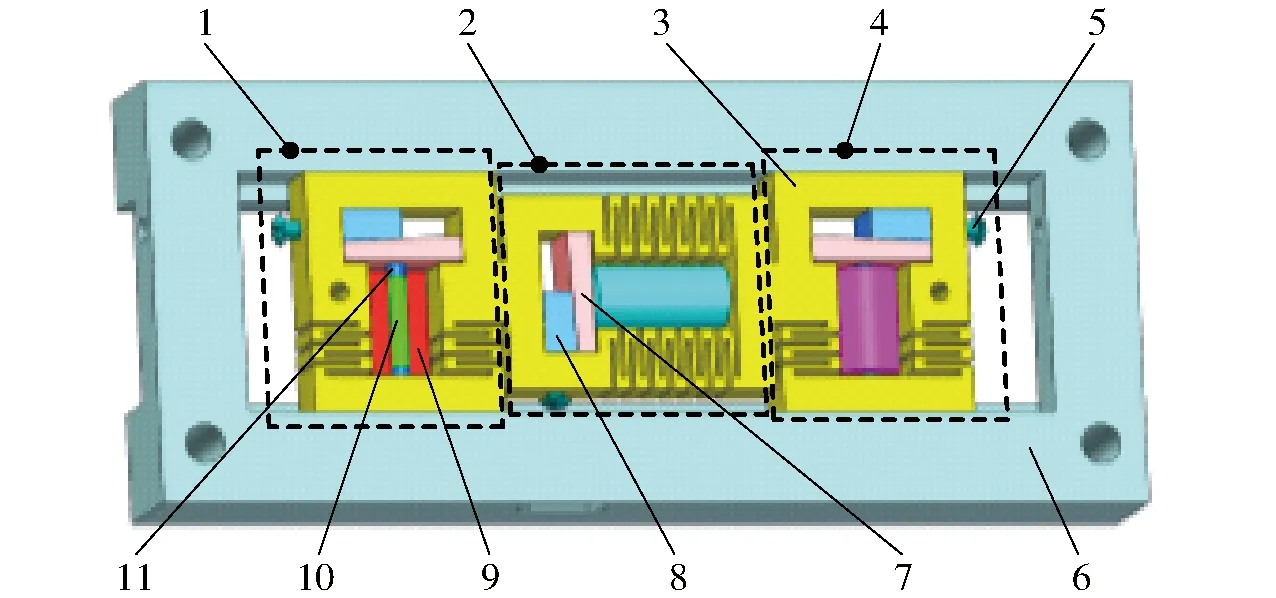
图2 结构组成Fig.2 Structure of actuator1.前箝位机构 2.驱动机构 3.动子 4.后箝位机构 5.螺钉 6.导轨 7.楔形块B 8.楔形块A 9.线圈 10.GMM棒 11.轭铁
2.2 叠加式柔性铰链设计
动子的弹性元件采用叠加式柔性铰链,与传统的单个柔性铰链相比,叠加式柔性铰链将形变分配到各个柔性铰链,大大地降低了柔性铰链的应力。采用的柔性铰链厚度为0.8 mm,若采用单个柔性铰链,刚度相同时其厚度减少为0.34 mm。对两种结构进行有限元分析(GMM棒输出位移为0.02 mm),其应力分布图如图3所示,单个柔性铰链的应力主要集中在柔性铰链的两端,最大应力为149 MPa,叠加式柔性铰链应力分布在各个柔性铰链,最大应力仅为16 MPa,叠加式柔性铰链的应力远远优于单个柔性铰链,有利于提高使用寿命。
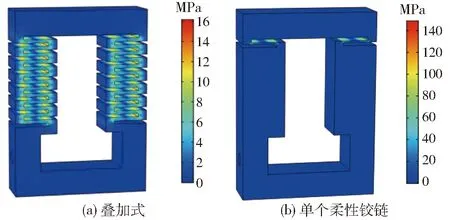
图3 叠加式和单个柔性铰链的压力分布Fig.3 Pressure distributions of superimposed and single flexure hinge
GMM棒输出位移时需克服柔性铰链的弹力,所以柔性铰链的刚度KR不能大于GMM棒的等效刚度KG,GMM棒的等效刚度KG为
(1)
式中FG——GMM棒输出力r——半径
S——输出位移lG——长度
λS——饱和磁致伸缩系数σ——应力
计算得驱动GMM棒等效刚度KG1=1.06×107N/m,箝位GMM棒等效刚度KG2=1.41×107N/m。
叠加式柔性铰链中各个柔性铰链的受力基本相同,受力分析如图4所示,柔性铰链的两端较厚部位假设成刚性,柔性铰链的A端固定,B端为自由端,C端受力F作用产生竖直位移,同时B端向左产生位移,此时,柔性铰链中点的弯矩为零,可将柔性铰链简化成在中点处销接的两个悬臂梁,销接处只受拉应力,由受力平衡得F1=F,由悬臂梁挠度公式得
(2)
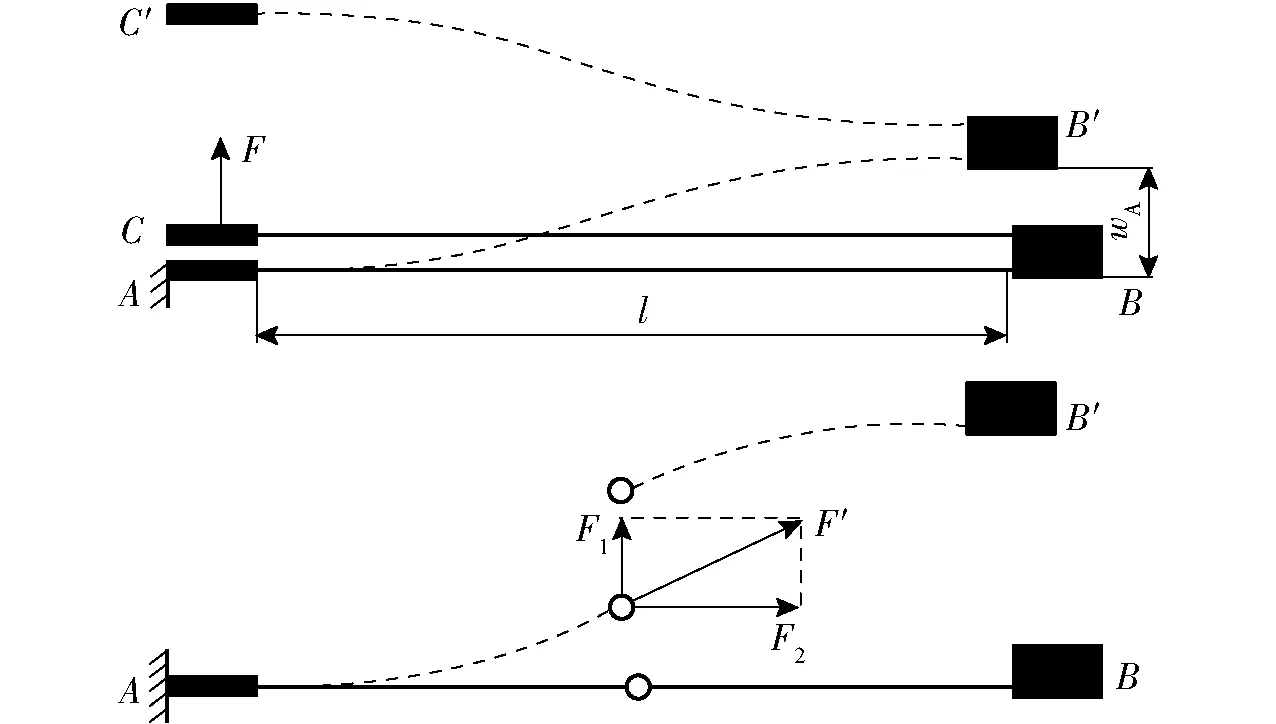
图4 柔性铰链受力分析Fig.4 Force analysis of flexible hinges
单个柔性铰链的刚度K为
(3)
式中wA——驱动柔性铰链的挠度
l——驱动柔性铰链长度
E——驱动柔性铰链弹性模量
IF——驱动柔性铰链截面惯矩
综合考虑强度、加工、寿命和尺寸等影响,单个柔性铰链尺寸为10 mm×6 mm×0.8 mm,驱动机构设置13对柔性铰链,箝位机构设置5对柔性铰链。通过计算得驱动柔性铰链刚度KR1=7.29×105N/m,小于KG1;箝位柔性铰链刚度KR2=1.89×106N/m,小于KG2,均满足设计要求。
2.3 预紧力和箝位设计
为发挥GMM棒的最佳输出性能,需要对GMM棒施加一定的预紧力,施加预紧力后,箝位机构和导轨的相对位置有3种情况,如图5所示,情况1是箝位机构和导轨有一定间隙,箝位机构箝紧时,需要克服箝位柔性铰链一定的弹性变形,箝紧力变小,这会降低驱动器的负载能力。情况2箝位机构和导轨接触并产生压力P,这种情况箝位机构移动时会产生摩擦力,也会降低系统的负载能力。情况3箝位机构和导轨刚好接触且不产生压力,即能最大程度地提供箝位力,又不影响系统的负载能力。由预紧力和柔性铰链刚度KR可确定箝位机构和导轨尺寸。

图5 箝位机构和导轨的位置关系Fig.5 Position relationship between clamping mechanism and guide rail
3 有限元分析
3.1 强度校核
为使柔性铰链有较好的弹性性能,材料选择65Mn弹簧钢。系统工作时,GMM棒来回伸缩,柔性铰链产生弯曲形变,应力集中在柔性铰链部位。对动子进行有限元分析,其应力分布如图6所示。从图6可看出,应力主要集中在柔性铰链的两端,最大应力为87 MPa,小于65Mn弹簧钢的极限强度785 MPa。对柔性铰链的疲劳强度进行仿真校核,在最高频率和最大受力的条件下,柔性铰链的疲劳寿命为1.17×1027次,可以看成具有永久寿命。
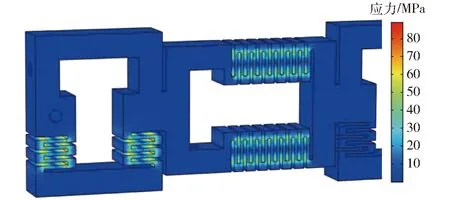
图6 动子的强度校核Fig.6 Strength checking of mover
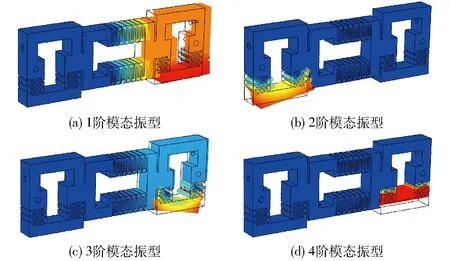
图7 动子模态分析Fig.7 Modal analysis of mover
3.2 模态分析
动子采用线切割一体化加工而成,驱动器工作时,驱动机构和箝位机构交替伸缩振动,为避免产生共振现象,需要对动子进行模态分析来确定其谐振频率。通过模态分析得前4阶模态振型如图7所示,前4阶谐振频率分别为388、948、1 072、1 374 Hz。通过实验确定驱动器的最大工作频率为150 Hz,未达到共振频率。
4 位移模型
为了简化复杂信号的分析,根据电路叠加原理,将单个正方波信号u(t)简化为2个幅值为U0的正负阶跃信号U(t)的叠加,如图8所示。

图8 正方波脉冲信号的简化叠加Fig.8 Simplified superposition of square wave pulse signals
U(t)表达式为
(4)
单个正方波脉冲函数u(t)可表示为
u(t)=U(t)-U(t-T0)
(5)
将线圈等效为电阻R和电感L的串联,如图9所示。开关闭合前的电流为零,即iL1(0-)=0,开关闭合的瞬间,由于电感L中的电流不能产生跃变,所以iL1(0+)=iL1(0-)=0,在电压U0的作用下,电感中的电流iL1逐渐增大,直至达到稳定状态iL1=U0/R。
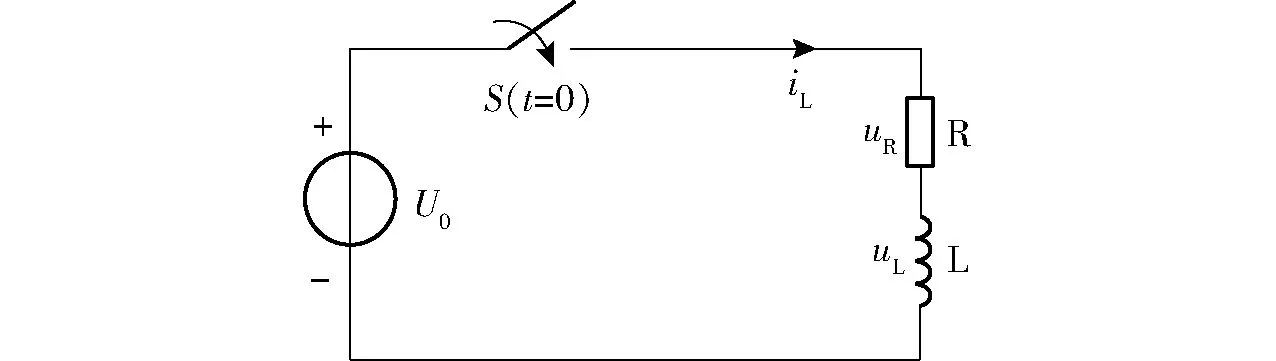
图9 线圈简化成RL电路图Fig.9 Circuit diagram of coil simplified into RL
对于正阶跃信号U(t),电感电流iL1的微分方程
(6)
式中R——电阻
L——电感
求解得电感电流iL1的响应为
(7)
同理,对于负延迟阶跃信号-U(t-T0),其产生的电感电流iL2的响应为
(8)
由叠加原理得激励线圈电流I的响应为
(9)
线圈上电时产生磁场,磁路由“GMM棒-轭铁-动子-轭铁-GMM棒”形成回路,忽略空气隙对磁路的影响和漏磁现象,各零件的磁阻与磁导率呈反比,而GMM棒的磁导率远小于其他零件,GMM棒的磁动势占据了磁回路大部分的磁动势,可增加修正系数e表示GMM棒的磁场强度[6],即
(10)
式中n——线圈匝数lC——线圈长度
H——GMM棒的磁场强度
I——电流
磁化强度M由J-A模型求得
(11)
式中He——GMM棒的有效磁场强度
α——磁畴畴壁间相互作用系数
Hσ——预应力产生的磁场强度
Man——可逆的无磁滞磁化强度
MS——饱和磁化强度
a——无磁滞磁化强度形状系数
Mirr——畴壁移动产生的不可逆磁化强度
Mrev——畴壁转动产生的不可逆磁化强度
δ——常数
k——不可逆损耗系数

c——可逆系数
应变模型采用基于能量法的二次畴转模型,即
(12)
式中λ——磁致伸缩应变
λS——饱和磁致伸缩系数
将GMM棒和柔性铰链简化成“质量-弹簧-阻尼”元件,GMM棒输出端、负载和柔性铰链刚性相连,具有相同的位移、速度和加速度,超磁致伸缩驱动器的动力学过程可简化为等效单自由度力学模型,如图10所示,图中MG、KG和CG分别为GMM棒的等效质量、等效刚度和等效阻尼,MR、KR和CR分别为叠加式柔性铰链的等效质量、等效刚度和等效阻尼,ML为负载等效质量,y为位移。
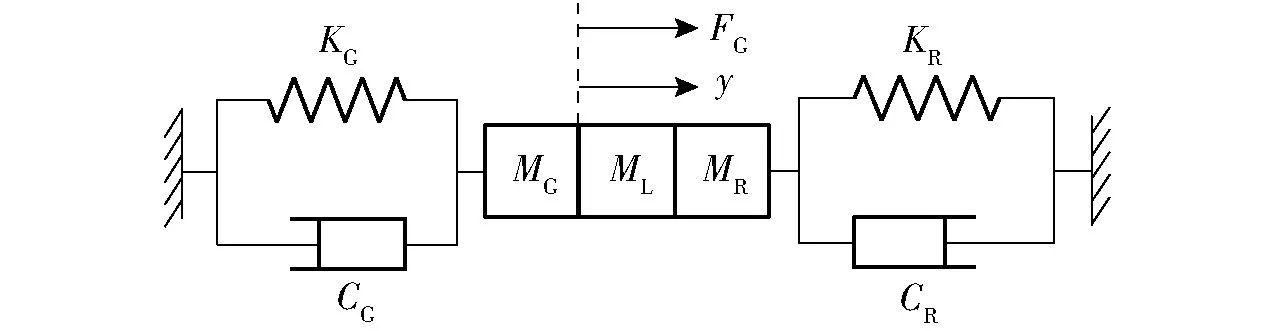
图10 等效力学模型Fig.10 Equivalent mechanical model
驱动器的动态微分方程为
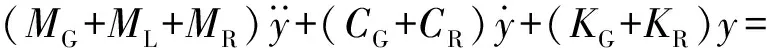
(13)
式中EH——GMM棒的杨氏模量
A——GMM棒的横截面积
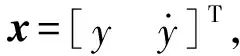
(14)
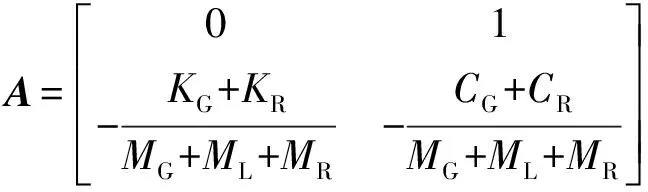
5 实验和结果分析
5.1 实验系统
动子采用线切割技术整体加工而成,为保证硬度进行淬火处理;驱动和箝位GMM棒尺寸分别为φ3×20 mm和φ3×15 mm;驱动和箝位线圈匝数分别为270匝和230匝;漆包线线径为0.41 mm,激光测距仪的分辨率为0.03 μm。样机安装在光学平台上,以减少外界环境对实验系统的影响,实验系统如图11所示。

图11 实验系统Fig.11 Experiment system1.样机 2.激光测距仪
5.2 输出位移特性分析
当频率f=1 Hz、钳紧电压为2 V时,在不同驱动电压下,系统位移输出特性如图12所示。在不同驱动电压下,输出位移曲线都呈阶梯状,表明设计的驱动器能够实现位移的累积输出,理论上导轨无限长时,直线驱动器的行程可达无限大。另外,每条阶梯状曲线的“踏面”并不平直,出现了5次规律性的振动,这是由于在一个周期内,系统除了进行“驱动”动作、还要进行“固定、解脱、复位”等5个动作,这些动作会对系统的位移输出产生影响。
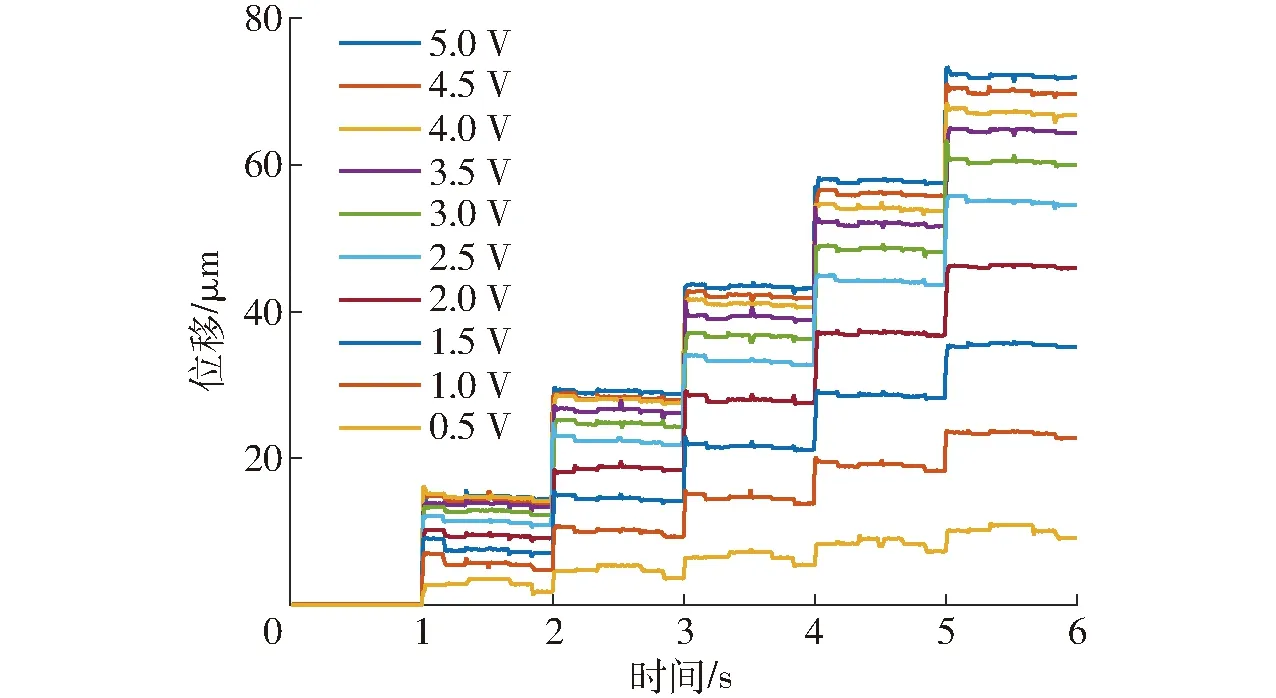
图12 输出位移特性曲线Fig.12 Output displacement characteristic curves
平均单步位移随驱动电压的变化规律如图13所示,在驱动电压较低时(<1 V),位移增长较缓慢;驱动电压达到中等电压时(1~3 V),输出位移基本呈线性增长;达到高电压时(>3 V),曲线的增长趋势又变得平缓。由于低电压时,GMM棒的应变主要是易磁化方向的部分磁畴增大,此时磁致伸缩应变响应很小。中等电压时,所有磁畴都旋转到易磁化方向,磁畴沿易磁化方向产生较大变化,磁致伸缩应变与磁场强度基本呈线性关系。达到高电压时,所有磁畴旋转到外磁场方向,磁致伸缩应变响应逐渐变小,逐渐达到饱和状态。位移-电压曲线的变化规律符合超磁致伸缩材料的性能特性[2]。
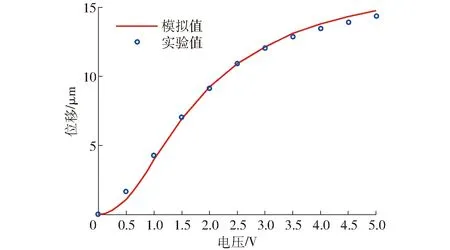
图13 位移-电压曲线Fig.13 Displacement-voltage curve
从图13可以看出,通过位移模型得到的模拟值和实验值基本吻合,电压较低时(<1 V),实验值略大于模拟值,主要由于驱动电压较低时,外界振动等因素对输出位移的影响较大,输出位移含有部分的外界振动。电压达到中等电压时(1~3 V),模拟值和实验值基本重合,最大相对误差为1.86%。电压较高时(>3 V),实验值逐渐低于模拟值,由于未设置散热装置,线圈的温升造成GMM磁致伸缩系数的减小,使得实验值低于模拟值。
图14为不同驱动电压下的单步位移变化曲线,驱动电压为0.5 V时,由于输出位移较小,分步动作和外界对输出稳定性的影响较大,最大相对误差达到了6.33%,位移输出稳定性较差。随着驱动电压的增大,位移输出逐渐变得稳定,最大相对误差减少至2.69%。另外,实验中发现当驱动电压大于3 V时,长时间工作时驱动线圈开始出现发热现象。综上所述,为保证驱动器的输出精度和工作状态,将工作电压设定为1~3 V,此时,驱动的最小单步位移为4.55 μm,最大单步位移为12.01 μm。
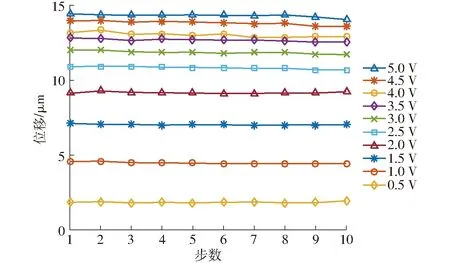
图14 单步位移的稳定性Fig.14 Stability of one-step displacement
驱动电压为2 V时,输出速度随频率的变化规律如图15所示,随着频率增加,输出速度基本呈线性增长,但频率大于150 Hz时,由于振动、响应等因素的影响,在一个周期内,系统不能完全完成“固定、解脱”等6个分动作,输出速度开始下降。所以驱动器的最高工作频率为150 Hz,最快速度为1.34 mm/s。
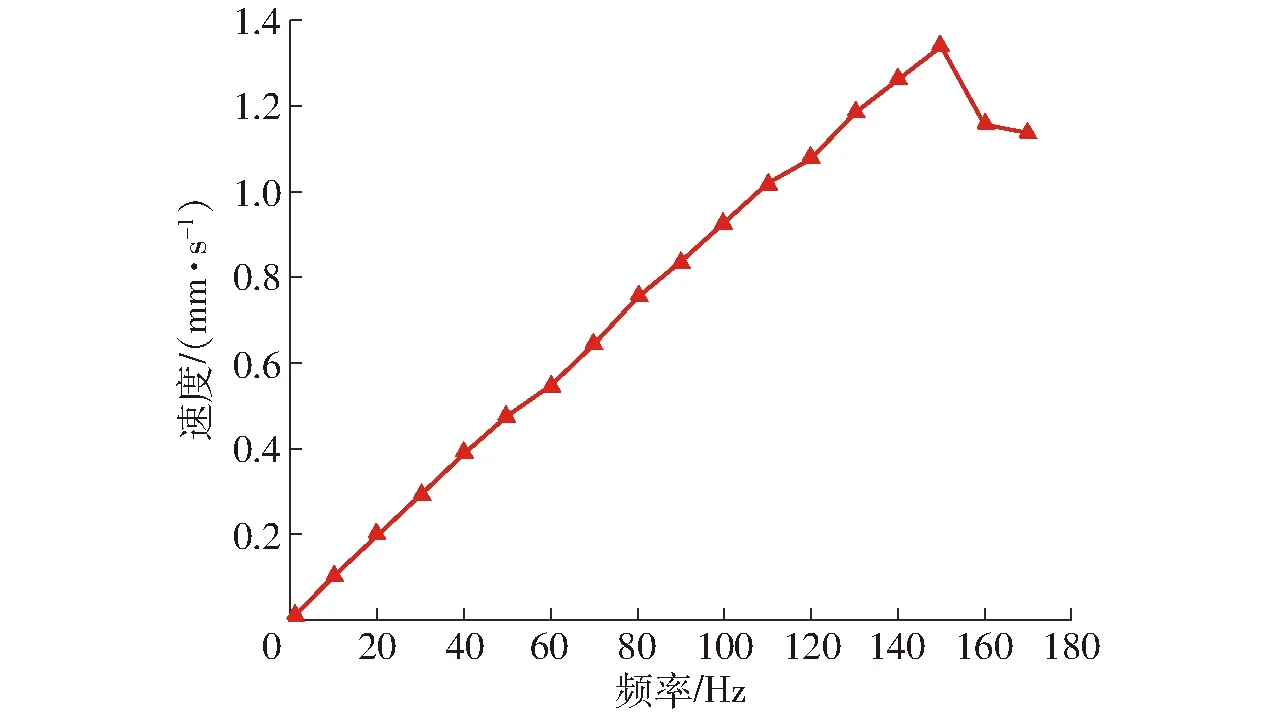
图15 速度-频率曲线Fig.15 Velocity-frequency curve
6 结论
(1)设计了一种基于尺蠖运动形式的大行程精密直线驱动器,实现了步进式位移输出。
(2)采用的叠加式柔性铰链有效改善了柔性铰链的受力情况,将柔性铰链简化成悬臂梁,计算出其等效刚度。
(3)建立的位移模型能够准确反映直线驱动器的输出位移,在工作电压范围内,最大相对误差为1.86%。
(4)经过实验测试,直线驱动器工作电压为1~3 V,最小和最大单步位移分别为4.55、12.01 μm,最高工作频率为150 Hz,最快速度为1.34 mm/s;位移输出状态稳定,最大相对误差为2.69%。

