基于分叉结构的穹顶温室试验与仿真优化

于海业 关姝杰 刘 爽 隋媛媛

(吉林大学生物与农业工程学院， 长春 130022)

0 引言

有限元仿真中，荷载施加、网格划分等前处理设置方法直接影响求解和后处理阶段。针对曲面不均匀及离散荷载，文献[1-2]将曲面离散为小单元的网格面或采用曲面分区拟合法，得出节点荷载，提高了计算效率。强风天气导致大跨度建筑屋顶积雪分布不规则、不固定，适宜的雪载模拟颗粒及融雪模型对结构设计至关重要[3-4]。对于温室及网壳建筑仿真，通常将风、雪等不固定荷载作用于节点或单元上[5-6]，不同网格尺寸对稳定性和强度有显著影响[7]。大型连栋玻璃温室单体面积可达30 hm2，单体面积的增加使得对建造设计要求更高，对风、雨、雪载等因素更加敏感，设计时需留出机械设备、智能化系统的进入端口，且须保证温室生产区域面积的合理最大化[8-12]。

穹顶温室整体为半球结构，内部配合螺旋栽培架可充分利用高度优势[13]。为了满足跨度、高度等可变要求，需寻求精确的仿真荷载施加方法及适宜大跨度结构的设计方法，在满足力学要求下尽量减少结构耗材。本文将最大雪载量按模型承力面面积比例进行分配施加，结合不同网格尺寸进行静力仿真，并与试验结果对比，得出仿真的准确度、跨度与网格尺寸的最佳匹配关系；对半径6 m的穹顶温室不同设计方案进行优化筛选，得出最优方案，以期为更大尺寸穹顶温室提供设计依据。

1 雪载试验与仿真

1.1 试验

1.1.1试验方法

穹顶温室缩尺模型(缩尺比例为1∶25[14])由上至下共4层，呈三角形逐级分叉结构，跨度为0.48 m，高度为0.24 m，下部2层屋顶坡度大于50°，理论上无雪载作用，为了得到更准确的试验数据，对上部3层进行试验与仿真(图1a)，取最大雪载量540 Pa[15]，已知模型总面积(上部3层全部三角形及梁的表面积之和)0.216 m2，可得试验中覆盖物(黏土，图1)总质量11.903 kg，根据每层总面积所占比例，可得每层覆盖物质量：第1层1.239 kg、第2层3.894 kg、第3层6.770 kg。将覆盖物均匀涂抹于模型上，由上层至下层逐一进行应变试验，第1层加载(图1b)，测试位置为第1层横梁和竖梁；第1、2层加载(图1c)，测试位置为第2层横梁和竖梁；第1、2、3层加载(图1d)，测试位置为第3层横梁和竖梁。采用BFH120-3AA型应变片作传感元件进行单桥式连接，应变片电阻为R=(119±1) Ω，敏感栅尺寸3.0 mm×2.3 mm，灵敏系数K为1%～3%。试验中设置一块温度补偿片，并将电桥桥盒接地，利用DH3817型动静态应变测试仪进行数据采集[14]。应变片粘贴方式见图2，试验中采用逐级加载方式，将每层覆盖物均分成4份，分4次加载，每组试验重复3次，采集频率为50 Hz，待数据趋于稳定时，持续30 s，提取稳定微应变均值作为试验结果。

图1 雪载试验模型及方法Fig.1 Model and method of snow-loaded test

图2 应变片粘贴方式Fig.2 Strain gauge pasted types

1.1.2试验结果与分析

预试验得出第3层横梁及短竖梁的微应变很小，因此只考察第3层长竖梁微应变变化情况(表1)。上部3层微应变绝对值(表1负号表示应变方向)随加载质量增加而增加，回归分析结果表明微应变与加载质量呈线性相关，相关系数为0.993 2～0.999 9。上部3层微应变，横梁大于竖梁，是由于横梁承力面宽度为3 mm，竖梁承力面宽度为15 mm，对于承力面面积，横梁小于竖梁；第2层竖梁及横梁微应变皆最大，说明第2层对雪载响应最显著，与文献[14]研究结果相同。

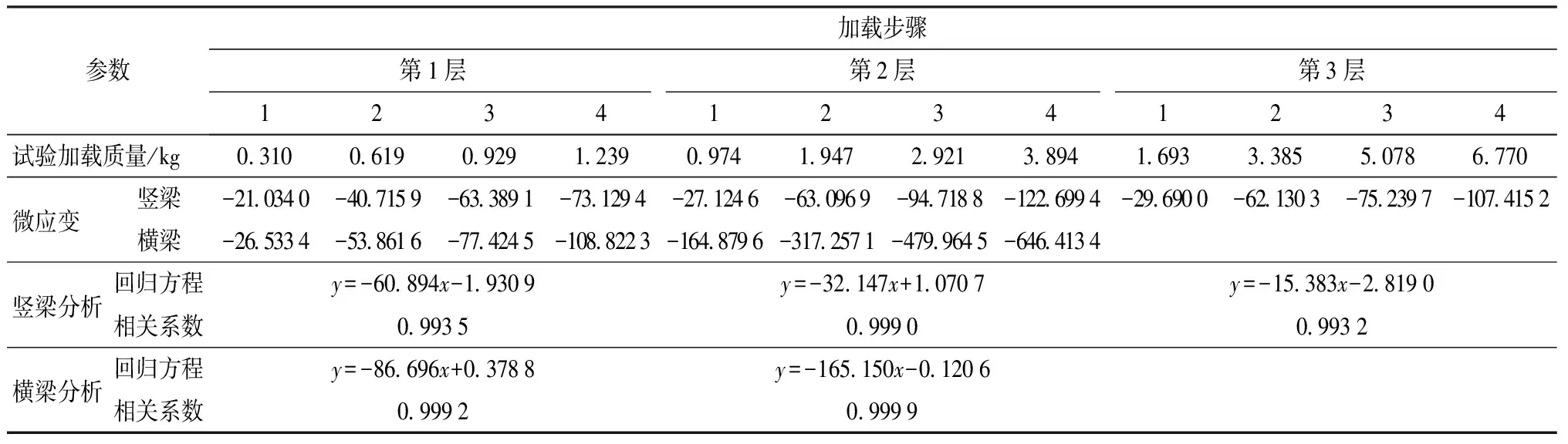
表1 微应变与试验加载质量回归分析Tab.1 Regression analysis of micro-strain and loading quality in tests

1.2 仿真

利用ANSYS 15.0 Mechanical界面对最优穹顶温室上部3层进行雪载仿真静力分析，提取每层横梁和竖梁的变形量，计算相应微应变，与试验结果对比，得出穹顶温室半径与仿真网格尺寸的最佳配合关系及仿真加载最优方法的准确度。

1.2.1加载方法

仿真加载值为雪载模拟试验中黏土的水平投影重量，图3(以竖梁为例)为试验与仿真荷载施加方向。仿真荷载采用两种计算方法：①将每层面积最大三角形区域按中心点分成3小块，按横梁和竖梁所在小块三角形面积与相应层总面积的比值计算相应重量作为横梁和竖梁仿真加载值。② 按每层横梁和竖梁所占相应层总面积的比值计算每根梁承载数值。选择两种结果中较大值作为仿真加载值，与试验值进行对比分析，此部分选择第2种，见表2。有限元计算中，网格尺寸过大会影响计算精度，过小会增加计算难度和时间，因此，合适的网格尺寸设置对仿真分析结果有重要影响[16-18]，本文将网格单元长度分别设置为10、12、16、18、20 mm，对第1层横梁(F=0.146 0 N)和竖梁(F=0.744 5 N)加载(表2)，提取不同网格尺寸下变形量，计算微应变，以仿真值与试验值的相对误差为指标，优选出穹顶温室模型最适宜网格尺寸。

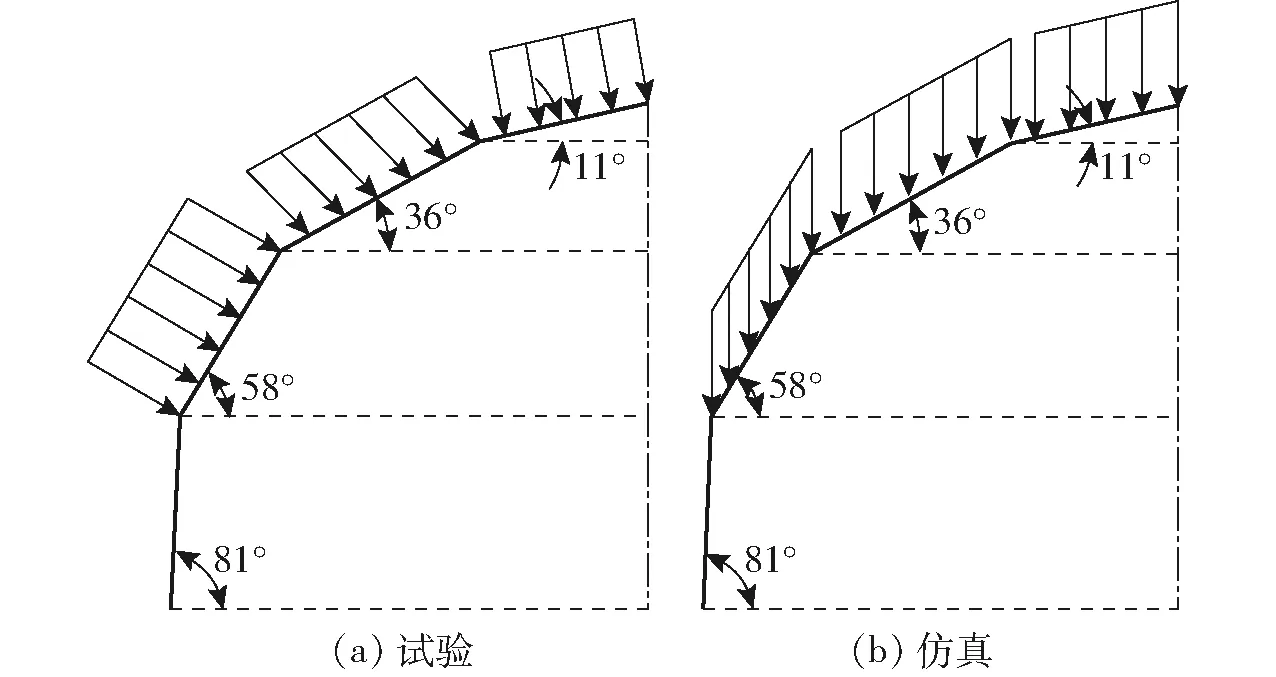
图3 荷载施加方向Fig.3 Directions of applied loads

表2 仿真加载值Tab.2 Simulated loading values

对模型分4次逐级加载，每层每级横梁和竖梁加载值见表2，根据应变片粘贴位置及方向(图2)，微应变计算中，横梁原长度取梁宽度，竖梁原长度取1/2梁长度，计算式为[19]

(1)

式中με——微应变

ΔL——变形量，mm

L——原长度，横梁取15 mm，第1层竖梁取46.82 mm，第2层竖梁取58.64 mm，第3层竖梁取69.19 mm

1.2.2仿真与试验结果对比

由表3可知，变形量与微应变的绝对值随网格长度的增加而减小，在网格长度为16、18、20 mm时趋于稳定，说明网格尺寸为16～20 mm较适宜；已知第1层全部加载试验中，横梁微应变为-108.822 3，竖梁微应变为-73.129 4(表1)，结合仿真值与试验值的相对误差，横梁在16、18、20 mm时较小且相近，竖梁在16、18 mm时较小且相近，得出穹顶温室半径在0.24 m时，适宜的仿真网格单元长度为16～18 mm，本文静力仿真中网格单元长度设置为16 mm。

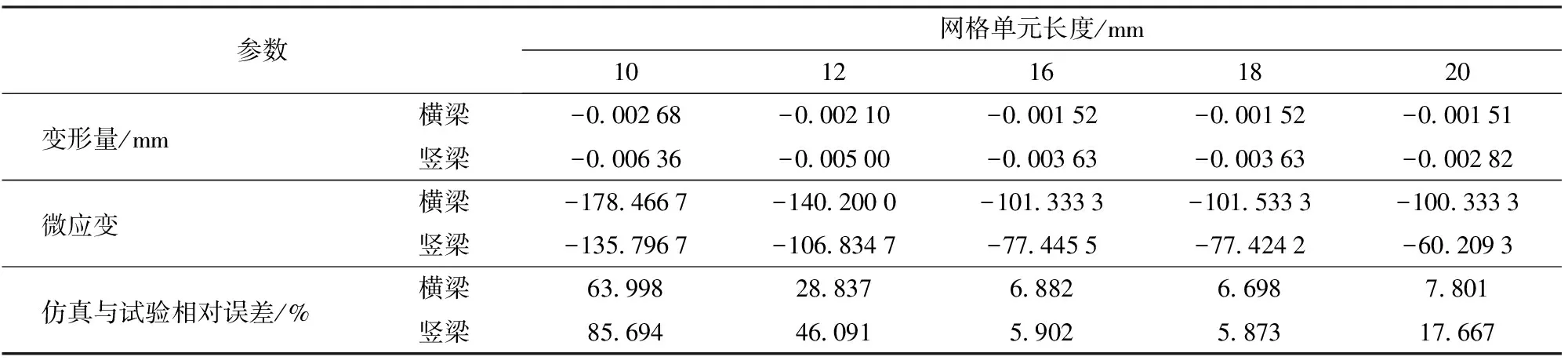
表3 不同网格单元长度第1层横梁和竖梁加载仿真结果Tab.3 Simulation results of the first layer loading at different mesh sizes

由图4可知，仿真与试验微应变与加载质量皆呈线性相关，试验相关系数见表1，仿真相关系数：第1层横梁和竖梁为1，第2层横梁为0.999 9、竖梁为0.999 5，第3层竖梁为0.994 8。试验与仿真微应变绝对值相近，皆随加载质量增加而增加，试验绝对值多略大于仿真值，是由于外部环境干扰及测量误差导致。微应变在仿真与试验中的相对误差为1.840%～8.386%(表4)，表明网格单元长度为16 mm，按横梁及竖梁面积所占比例计算加载值的仿真方法能够反映穹顶温室真实承载特性。

图4 仿真与试验微应变对比Fig.4 Comparison of micro-strain between simulation and test

2 结构优化设计与仿真

2.1 半径6 m穹顶温室结构优化

采用试验优化设计方法，给出主要因素及相应水平，确定评价指标，将所有结构设计方案(以Auto CAD 2010为设计软件)进行逐步优选，最终得出半径为6 m穹顶温室最优结构方案，为穹顶温室尺寸扩展提供设计依据。

2.1.1结构初选

所有方案中，同一层呈对称结构，不同层采用不同分叉模式，表5中按层数逐级分叉主要结构为“1-2-4”，混合分叉主要结构为“1-3-2”。共12

表4 仿真与试验中微应变相对误差Tab.4 Relative errors of micro-strain between simulation and test %

表5 试验因素水平及设计方案Tab.5 Test factor levels and design schemes

组设计方案(表5)，采用简单比较法，设置3个边界条件：

(1)层数为3时，结合结构稳定性和强度要求，第1层梁数设计为8；层数为5时，为避免用钢量过大，第1层梁数设计为6。因此排除A1B1C1、A1B1C2、A3B2C1、A3B2C2。

(2)由文献[14]可知，4层逐级三角形分叉结构在不同荷载组合作用下，最大位移区域在第2层，第3层为主要承载区域，结构最复杂，底层位移皆最小，采用一分二结构即可，因此逐级分叉结构只适用于中间层数的设计，不适宜3层结构，排除A1B2C2。

(3)为减小结构质量，钢材为Q235薄壁型方钢管，壁厚设置为1.5 mm，根据不同设计方案采用不同外径，最大长细比小于200[20]，可得所剩7组方案最小外径尺寸及理论最小用钢量，见表6。可知，逐级分叉结构由于第2层横梁尺寸较大，需要较大外径钢管，因此用钢量较大，排除两组用钢量最大的设计方案，即A2B1C2及A3B1C2，只留A2B2C2用于后续力学校验对比分析。

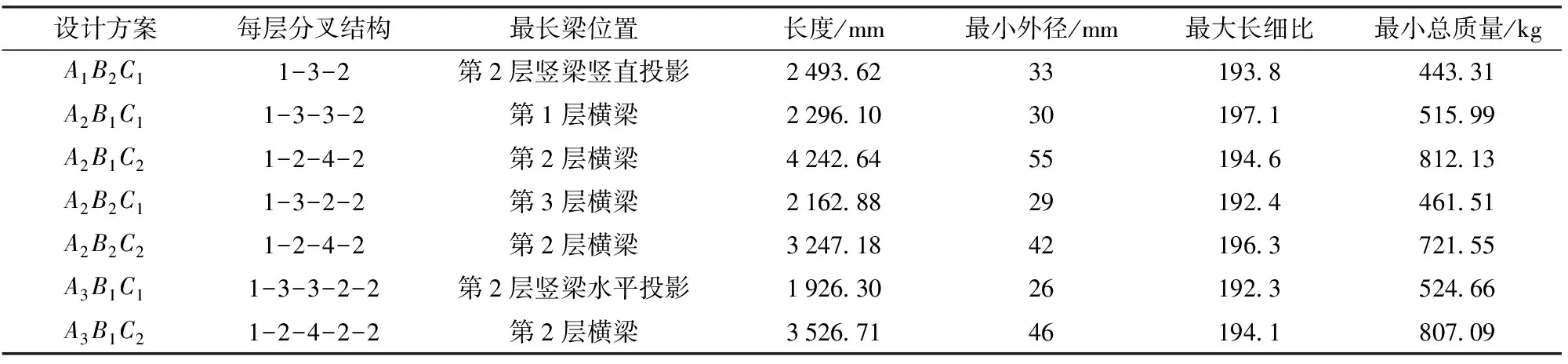
表6 钢材尺寸及整体最小用钢量Tab.6 Steel dimensions and minimum steel consumption quantities

2.1.2线性屈曲分析

结构整体初始缺陷模式可按最低阶整体屈曲模态采用[20]，在ANSYS 15.0 Mechanical界面对所剩5组方案进行线性屈曲仿真分析，得出屈曲荷载及初始缺陷模式，排除初始缺陷较大设计方案。由雪载试验可得，在半径为6 m的穹顶温室仿真中，适宜的网格单元长度为20 mm×20 mm，材料为Q235薄壁型钢管，弹性模量E为2×1011MPa，泊松比μ为0.3。线性屈曲分析中，加载1 N的力，得到屈曲系数即为屈曲荷载，见表7。

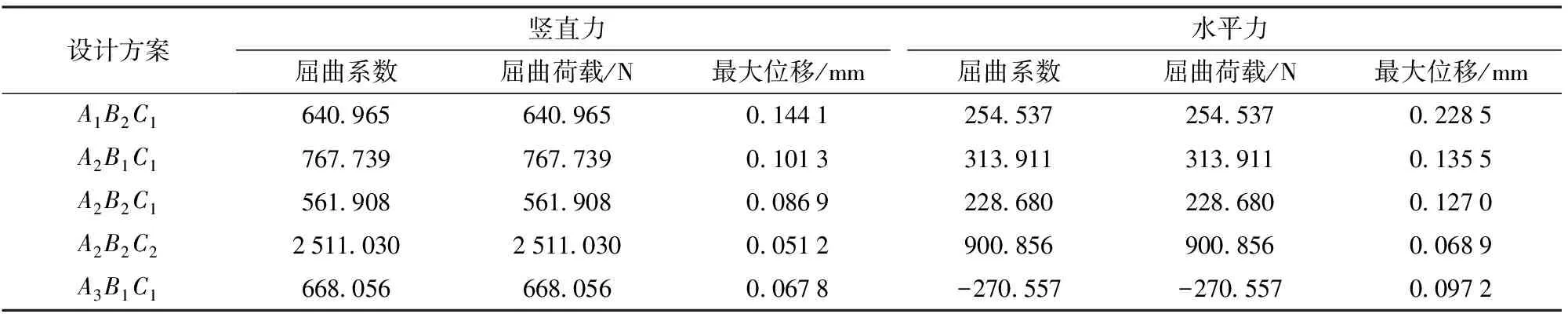
表7 5种结构线性屈曲结果Tab.7 Linear buckling results of five structures

由表7可知，5种结构的线性屈曲荷载在竖直方向大于水平方向，说明穹顶温室分叉结构对水平荷载响应明显。屈曲荷载在A3B1C1水平力作用下为负值，表面失稳状态与作用力方向相反，初始缺陷较大，其他4组在两方向的荷载由大到小为A2B2C2、A2B1C1、A1B2C1、A2B2C1，表明逐级分叉结构承载力最优。结合图5，在Z轴负方向施加竖直力，蓝色线条为最大位移区域，在X轴正向施加水平力，红色线条为最大位移区域，5组中的最大位移(表7)，A2B2C2在两方向力作用下皆最小，大变形区域最少在第2层横梁(图5d、5i)；其次是A3B1C1，大变形区域在竖直方向主要在第2层竖梁(图5e)，在水平力作用下分布不均，在第2、3、4层皆有出现(图5j)；A2B1C1与A2B2C1相近，大变形区域主要在第2层长竖梁(图5b、5c、5g、5h)；A1B2C1在两方向力作用下皆最大，大变形区域在第2层长竖梁(图5a、5f)。综合屈曲荷载与变形，A2B2C2初始缺陷最小，安全性最好，其次是A2B1C1、A1B2C1、A2B2C1，A3B1C1几何缺陷明显，大变形区域分散，故排除。

图5 5种结构线性屈曲模态Fig.5 Linear buckling modes of five structures

2.1.3力学校验

对所剩4组方案进行刚度、强度及稳定性校验，以得出最合理的设计方案。在ANSYS 15.0 Mechanical界面，对4种结构进行静力仿真，网格单元长度为400 mm，底部横梁全部约束，加载方式为力，将每层最大三角形面积的1/3与相应层总面积的比值乘以相应层荷载组合总值，计算所得为相应横梁和竖梁的荷载组合值，除以节点数(梁长除以400 mm，同一层对于不同长度的竖梁，取短梁长度进行计算)，得出每根横梁与竖梁的仿真加载值(半径为0.24 m，此种横竖梁加载方式与本文1.2.1节所述加载方法数值相近，1.2.1节所用方法数值略高，仿真结果更清晰；而半径为6 m时，两种方法数值相差较大，故采用上述方法更接近实际情况)。

受力形式为荷载组合方式：组合1(恒载+雪载)，竖直向下；组合2(恒载+风载)，水平向右(只考虑垂直屋脊方向，且结构呈对称分布)。荷载组合按每层分开计算，恒载为梁及覆盖材料(双层中空玻璃，面密度ρ为25 kg/m2)重量之和，作用在水平投影上；雪载取最大值，作用在水平投影上，计算式为[15]

Sk=S0μrCeIeCtg

(2)

式中Sk——雪载标准值，kPa

S0——基本雪压标准值，取0.3 kPa

μr——屋面积雪分布系数，第1层屋顶坡度小于25°，取1.0；第2层A1B2C1屋顶坡度平均值为45°，取0.2，其他3组屋顶坡度平均值为35°，取0.6，第3、4层屋顶坡度皆大于50°，取0

Ce——场区暴露系数，取1.0

Ie——结构重要性系数，取1.0

Ctg——采暖系数，取1.0

风载取最大值，作用在竖直投影上，计算式为[15]

Wk=W0μzμs-W0K0

(3)

式中Wk——风载标准值, kPa

W0——基本计算风压, 取0.5 kPa

μz——风压高度变化系数，第1、2层取1.0，第3、4层取0.8

μs——温室风荷载体形系数，取0.6

K0——温室附加风荷载系数，取0.2

梁的刚度可用梁的最大挠度来衡量，受弯主梁的最大挠度(本文用最大位移表示)允许值为[21]

w=l/400

(4)

式中w——梁最大挠度允许值，mm

l——梁跨度(按水平和投影方向折算长度，取最大值)，mm

A1B2C1、A2B1C1理论最小外径(表6)经仿真验算，不符合刚度要求，将其分别调整为40、32 mm。

考虑内力和弯矩作用，平面外稳定性计算式为[22]

(5)

式中N——最大轴力, N

φ——轴心受压构件稳定性系数[23]

A——构件截面面积，mm2

M——最大弯矩，N·mm

φb——梁的整体稳定性系数，对于闭口截面取1.4

W——截面抵抗矩，mm3

f——钢材强度设计值，取205 MPa[15]

根据第四强度理论，最大等效应力应小于钢材强度设计值(205 MPa)，以此检验温室强度[14]。

力学校验相关参数及仿真中所有节点加载值见表8。

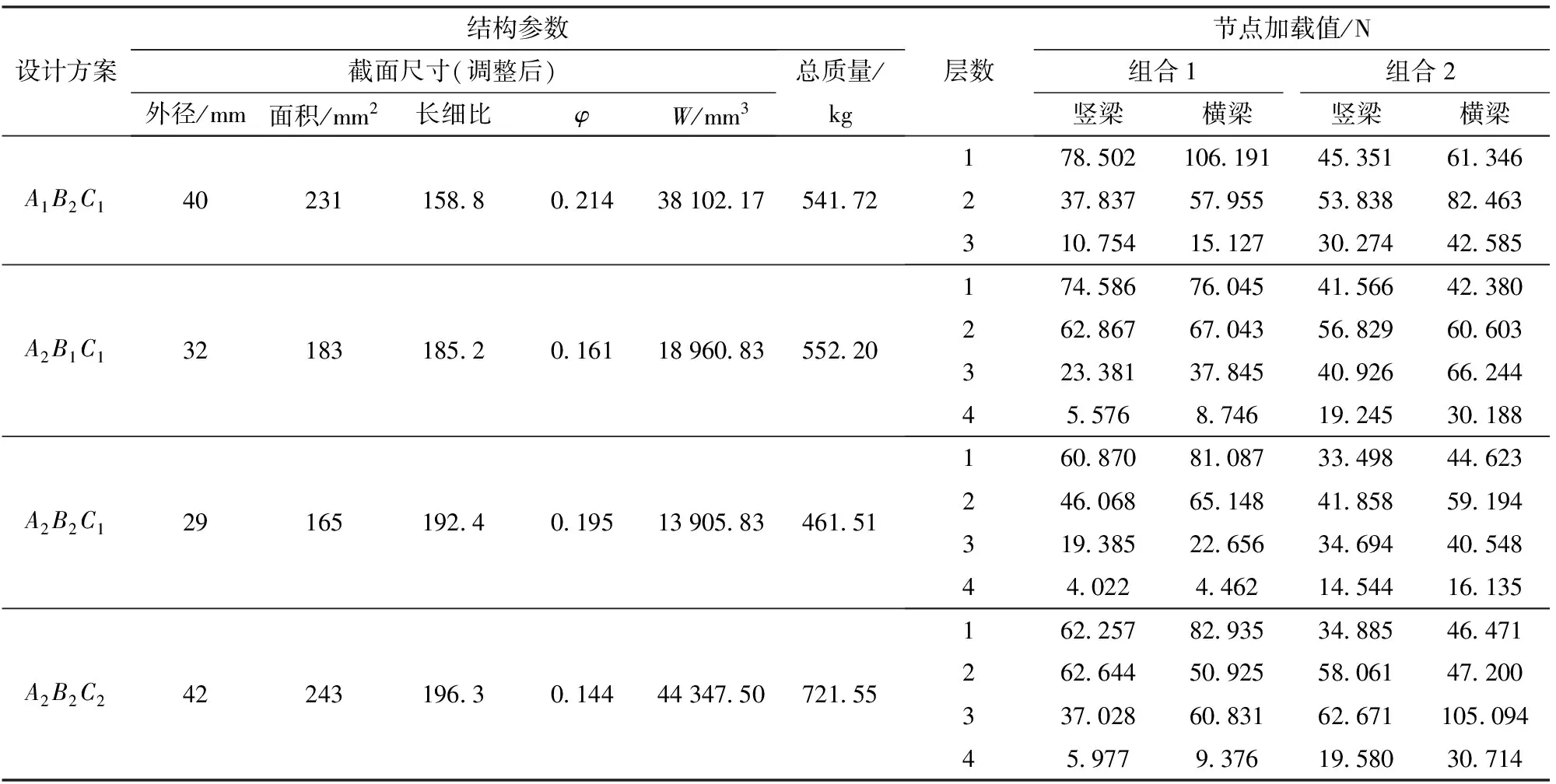
表8 结构参数及仿真加载值Tab.8 Structural parameters and simulation loading values

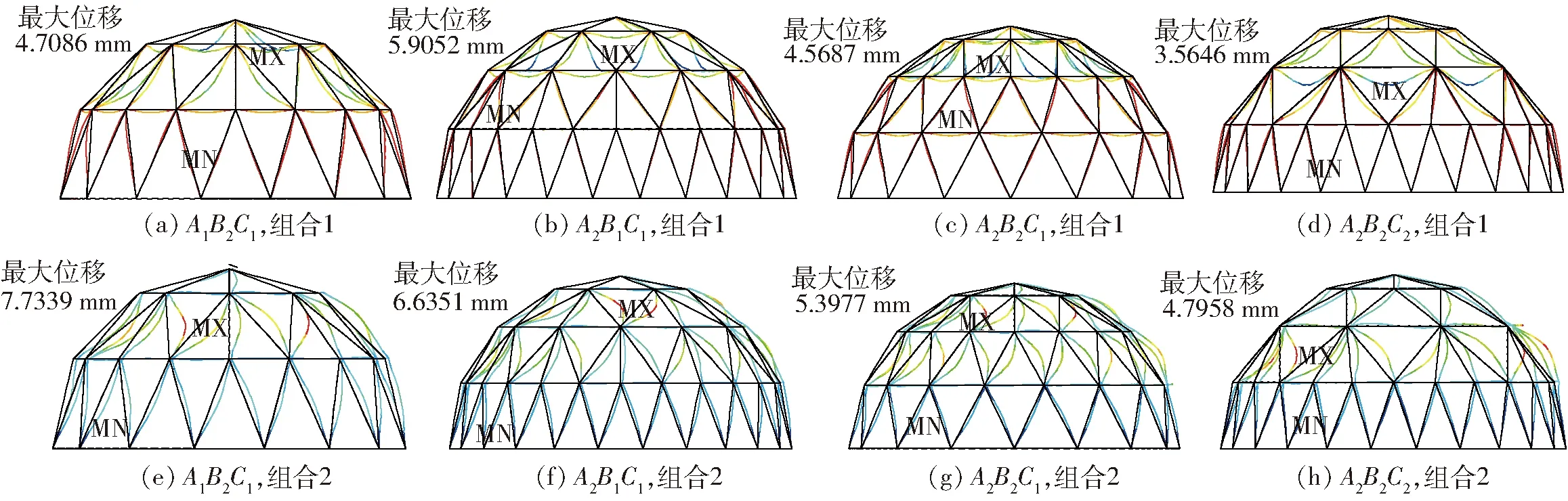
图6 4种结构最大位移Fig.6 Maximum displacement of four structures

所有梁的最大位移皆小于相应最大挠度允许值，符合刚度要求。由图6可知，加载前结构为黑色线条，加载后变形为彩色线条，组合1，蓝色线条为最大位移区域；组合2，红色线条为最大位移区域。水平荷载对4种结构最大位移影响更大，整体变形随加载方向垂直下压及向右偏移，没有扭转变形。组合1作用，最大位移由大到小为A2B1C1、A1B2C1、A2B2C1、A2B2C2，组合2作用，最大位移由大到小为A1B2C1、A2B1C1、A2B2C1、A2B2C2，对于刚度，A2B2C1及A2B2C2相对较优；A2B2C1最大位移区域在2种组合作用下皆为第2层长竖梁，A2B2C2最大位移在组合1作用下为第2层横梁，组合2作用为第3层长竖梁，A2B2C1最大位移区域范围小，更利于结构优化加固。

在ANSYS结果中提取每组最大轴力、弯矩及最大等效应力，以检验结构在弯矩作用下局部极限稳定性及强度，结果见表9，4种方案稳定性和强度皆小于205 MPa，符合设计要求。2种荷载作用下，稳定性最优方案皆为A1B2C1，强度最优为A2B2C2，是由于此2种方案钢材外径较大，4组相比，校验结果差别不大，在满足长细比及刚度要求时，稳定性及强度皆远小于钢材设计值，说明穹顶温室分叉结构刚度变化值为首要设计条件。

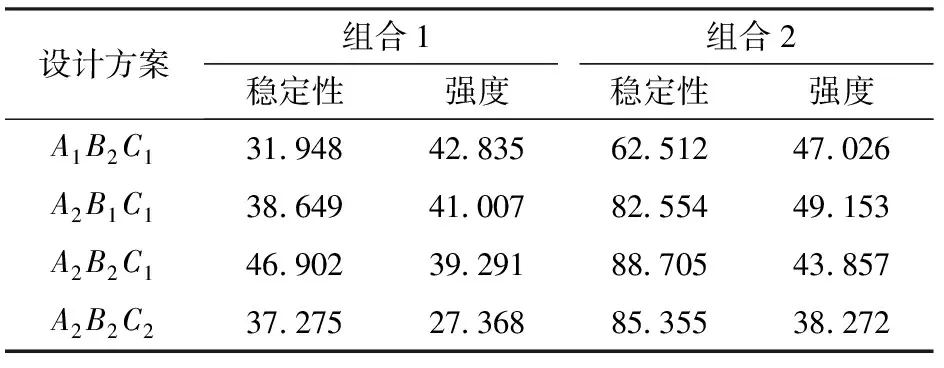
表9 4种结构稳定性、强度Tab.9 Stability and strength values of four structures MPa

刚度、强度及稳定性满足设计条件时，钢材质量越小越好，因此在半径大于等于6 m时，最优方案为A2B2C1(表8)，即共4层、第1层梁数为8、混合分叉结构。穹顶温室体积按半球近似计算，可得半径6 m穹顶温室用钢量为1.02 kg/m3。

2.2 半径12、18 m穹顶温室结构的设计

2.2.1结构设计与仿真方法

采用混合分叉结构，分别对半径为12、18 m的穹顶温室进行优化设计，以用钢量、刚度、强度及稳定性作为指标对两尺寸最优结构进行校验，在ANSYS中，网格单元长度设置为400 mm(与半径为6 m结构相比，梁长度相差不大)，采用相同仿真加载值计算方法，结构相关参数见表10。现有1 152 m2Venlo型连栋玻璃温室用钢量约为1.82 kg/m3[10]，半径为12 m穹顶温室用钢量为0.74 kg/m3，半径为18 m穹顶温室用钢量为1.09 kg/m3(表10)，结合半径6 m结构，穹顶温室用钢量可节约40.11%～59.34%。

表10 半径为12、18 m穹顶温室结构参数Tab.10 Structural parameters of dome greenhouse with radius of 12 m and 18 m

由于12、18 m结构存在较多长细比大的薄壁构件，因此对两结构在竖直和水平荷载下进行非线性屈曲分析，首先进行线性屈曲仿真，加载值为1 N，得到线性屈曲系数即为线性屈曲临界荷载，打开大变形开关，采用弧长法，引入线性屈曲模态作为初始缺陷模型[24]，加载值为线性屈曲系数1.2倍的近似值，提取最大位移区域所在节点荷载-位移曲线读取初始直线段部分荷载最大值，即为结构失稳的实际临界荷载[25]。

2.2.2力学分析结果

图7中荷载为支座反力，与加载值反向，位移与加载值同向，两者采用绝对值进行分析。在不同荷载方式作用下，两结构荷载皆随位移增加而增大，初始阶段，荷载与位移呈线性关系，结构处于线弹性变形阶段，随后进入塑性变形阶段，直至失效。结合表11屈曲分析结果，水平荷载作用、线性屈曲荷载与加载力反向，有明显初始缺陷，有必要对大跨度穹顶温室进行非线性分析。图7辅助线标记部位为非线性屈曲荷载，见表11，可知两结构竖直加载，非线性屈曲荷载平均为线性屈曲荷载的0.37倍，水平加载，非线性屈曲荷载平均为线性屈曲荷载的0.57倍，说明非线性屈曲结果是接近实际和保守的，且非线性屈曲荷载皆大于相应组合1、2的加载值，说明结构安全。

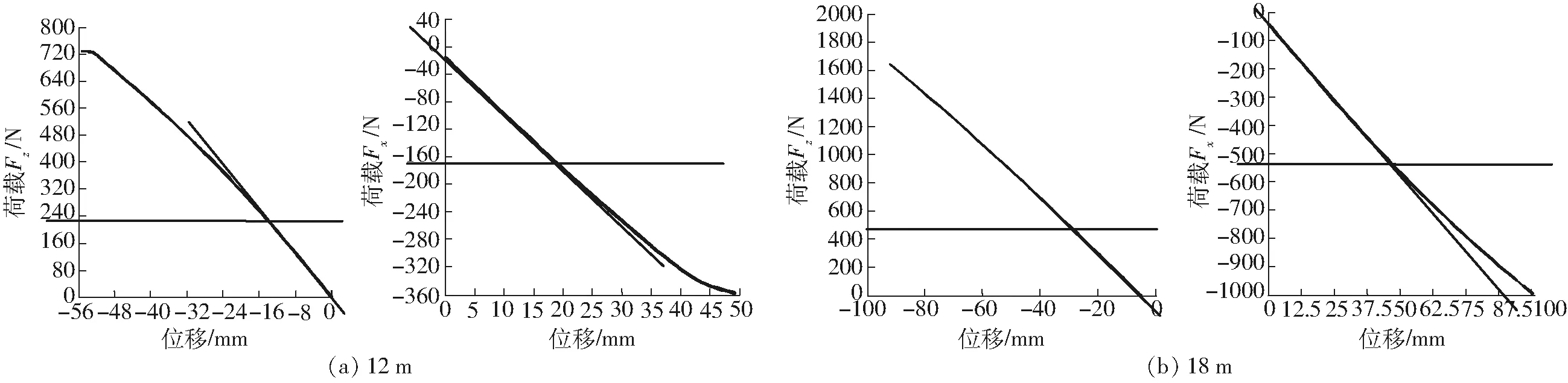
图7 半径为12、18 m穹顶温室非线性屈曲荷载-位移曲线Fig.7 Nonlinear buckling load-displacement curves of dome greenhouse with radius of 12 m and 18 m

对两结构进行力学校验，最大位移区域(图8)，组合1为蓝色线条，组合2为红色线条，组合1作用，12 m结构位于第2层长竖梁，18 m结构位于第3层长竖梁，两者分叉模式皆为一分三；组合2作用，12 m集中在上部4层长竖梁，18 m位于第3、6层长竖梁(此两层分叉模式为一分三)，以及第2、4、5 层横梁(此3层横梁长度较大)。经验算，所有梁的最大位移皆小于相应最大挠度允许值，符合刚度要求，

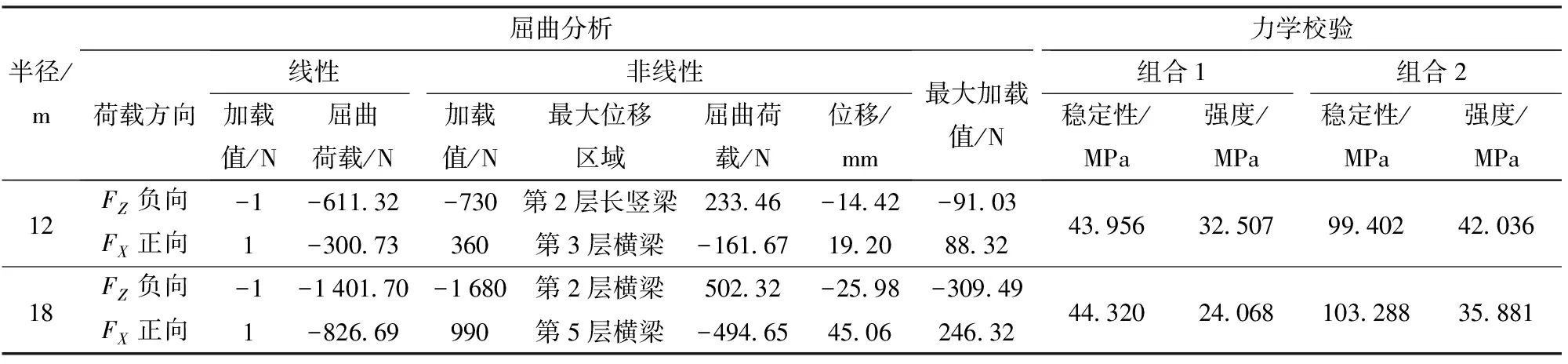
表11 半径为12、18 m穹顶温室力学分析结果Tab.11 Mechanical analysis of dome greenhouse with radius of 12 m and 18 m

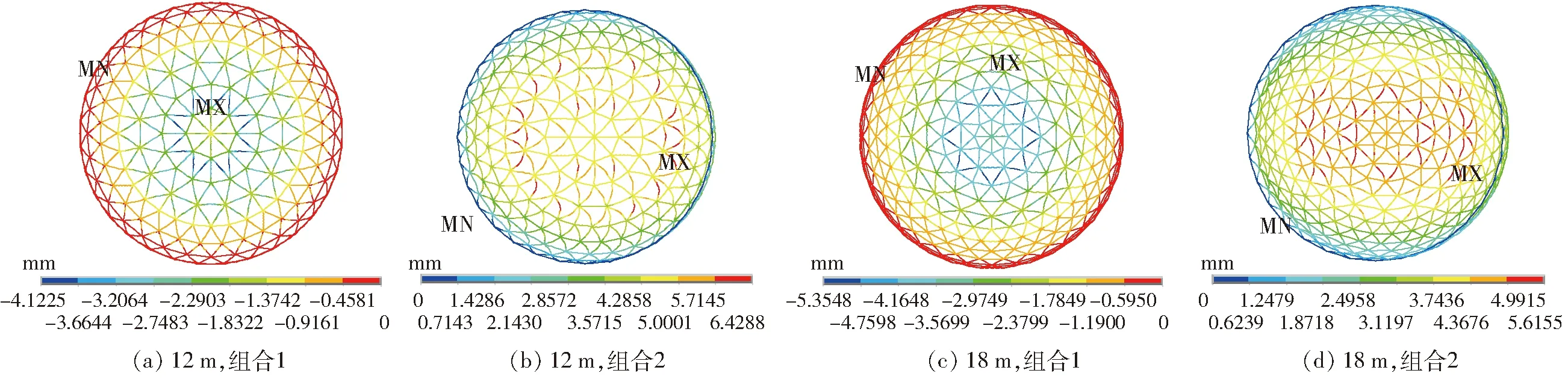
图8 半径为12、18 m穹顶温室最大位移Fig.8 Maximum displacements of dome greenhouse with radius of 12 m and 18 m

稳定性和强度皆小于205 MPa，符合设计要求(表11)，结合表9A2B2C1方案，6、12、18 m的稳定性皆在组合2作用下响应明显，表现为在组合2作用分别为组合1作用的1.89、2.26、2.33倍，强度在2种组合作用下差别不大，3种结构力学校验数值差别不大，表明此种设计方法在满足刚度条件下，稳定性和强度皆可符合要求且近似稳定。

3 结论

(1)对最优穹顶温室缩尺模型进行逐级雪载模拟应变试验，按模型承力面面积比例计算模型上3层横梁及竖梁相应荷载，在ANSYS中进行仿真对比，得出微应变在仿真和试验中的相对误差为1.840%～8.386%，且微应变与加载质量呈线性相关关系，相关系数为0.994 8～1，第2层竖梁及横梁微应变皆最大，说明第2层对雪载响应最显著；对1层横梁和竖梁加载，提取不同网格尺寸模型微应变，得出模型半径在0.24 m时，网格尺寸为16 mm最为适宜。

(2)在ANSYS中，按模型承力面面积比例计算仿真加载值，对半径6 m穹顶温室不同设计方案进行初选、线性屈曲、力学校验(刚度、强度、稳定性)分析，结合用钢量得最优方案为4层、第1层梁数为8、混合分叉结构。在此基础设计了半径为12、18 m的穹顶温室最优结构，由线性屈曲仿真可知，在水平荷载作用下，1阶初始模态与加载方向相反，有明显初始缺陷，进而进行非线性屈曲仿真，得到竖直和水平荷载作用下，非线性屈曲荷载平均为线性屈曲荷载的0.37倍和0.57倍，说明有必要对大跨度穹顶温室进行非线性屈曲仿真；力学校验结果皆符合要求，与1 152 m2Venlo型连栋玻璃温室相比，3种尺寸温室单位体积用钢量可节约40.11%～59.34%，其中，半径为12 m结构用钢量最小，应用时可优先考虑。