功能梯度圆柱壳的热应力与热传导分析
刘文光, 丰霞瑶, 姚 婉
(南昌航空大学 航空制造工程学院,南昌 330063)
功能梯度材料(functional graded materials,FGMs)是一种由陶瓷和金属、金属和金属、陶瓷和非金属、非金属和塑料、陶瓷和陶瓷等组合而成的复合材料,其结构和成分随体积的变化而变化。FGMs 结构的空间位置决定了材料的性能,因为空间位置不断变化,其性质沿一个或多个方向不均匀但连续变化。陶瓷金属基的功能梯度材料能承受2000 K 的表面温度热障,采用分层加工、熔体处理、颗粒处理等可控制剪切变形、腐蚀、磨损和屈曲,还能消除应力集中。优异的材料特性使FGMs能在高温情况下应用于航天器微电子、超音速飞机以及燃烧室热保护系统等。
飞机尾喷管一般装在涡轮发动机后端,它的作用是将管中流过的热能变为动能,并排出燃气。一般发动机尾喷口温度约为1100~1300 ℃,但是战斗机尾喷口温度可达1600~2000 ℃。随着战斗机飞行速度增加,发动机涡轮叶片转速增加,发动机内部会产生大量热量,导致发动机的四周壁温度极高。若热量无法及时散发出去,会直接影响发动机的工作性能。要提高发动机性能,尾喷口材料必须耐高温、抗冲击和耐腐蚀。考虑战斗机尾喷口工作温度条件,钛合金未必满足使用要求,普通陶瓷、金属和复合材料则更难满足条件。战斗机尾喷口使用金属基陶瓷功能梯度材料设计,不仅能避免金属和陶瓷之间因物理和力学性能上差异所导致的接触界面的应力问题,而且可缓解材料在使用中因高温梯度造成的热应力问题。即利用陶瓷的强散热能力,可将发动机内部的热量及时地散发到外界,降低发动机内壁温度,同时借助金属材料的高强度,可以保证战斗机尾喷口在飞行过程中的强度要求。
虽然FGMs 研究时间不长,但是发展十分迅速。特别在日本和欧美等工业比较发达的国家,FGMs 在组织结构、制备工艺及应用等方面都取得了令人瞩目的成就。针对FGMs 结构的热应力问题,Noda 等用含裂纹有限非均匀弹性体研究了FGMs 结构的稳定热应力及热应力强度因子[1];Cho等基于Crank-Nicolson-Galerkin 方案建立了FGMs壳的热应力分析模型[2]。围绕FGMs 结构的力学性能,Loy 等分析了金属基陶瓷FGMs 壳的力学特性[3];Xu 等测定了用粉末冶金法制备出的HATi 轴对称生物FGMs 的力学性能和热膨胀系数[4];Lin 等测试了利用微波烧结方法开发的WC/Co 重金属FGMs的微结构及硬度[5]。为优化FGMs 组织结构,曹文斌等研制了新的金属基FGMs,并应用于新一代核聚变托克马克实验室装置[6];刘文光等研究了热应力和热传导约束下FGMs 的最佳陶瓷体积分数指数[7]。考虑热环境对FGMs 板壳结构动力特性的影响,Shah 等引入Winkler 和Pasternak 提出的模量公式,修正了FGMs 圆柱壳的动力学方程[8];Wang等研究了含初始应力时热环境对FGMs 板振动的影响[9];刘文光等分析了温度变化和热应力对FGMs壳模态频率的影响[10]。基于近场动力学方法,刘英凯等建立了FGMs 的热传导模型,研究了在温度荷载作用下FGMs 的温度场,讨论了不同梯度形式对FGMs 热传导的影响[11]。陈金晓等采用改进傅里叶级数建立了FGMs 圆柱壳的振动特征方程,研究了在弹性边界条件下,壳体尺寸、陶瓷体积分数等因素对FGMs 圆柱壳固有频率的影响[12]。胡国栋等发展了用于研究FGMs 二维稳态热传导问题的数值流形方法,探讨了相关矩阵的求积策略[13]。黄怀纬等采用Donnell 壳体理论推导了FGMs 椭圆柱壳的屈曲控制方程及屈曲临界温度的解析表达式,分析了均匀分布、线性分布及非线性分布的温升环境对FGMs 物性的影响以及屈曲临界温度随截面离心率、材料组分参数的变化规律[14]。
战斗机高速飞行时,尾喷口热量过大容易产生变形,直接影响飞行性能。因此,战斗机起飞时,应收缩尾喷口增加推动比,缩短起飞距离,而在降落时,应扩张尾喷口增加阻力以减小滑行距离。也就是说,尾喷口的变形不仅影响起飞,而且影响战斗机飞行距离。对于带有弧度的尾喷口,热应力存在时极易导致尾喷口形状破损。发动机尾喷口一旦损坏,发动机内部的热量更难散发出去,若能将FGMs 应用于战斗机的尾喷口设计,或将改善战斗机工作性能。
飞机、导弹、战斗机尾喷口等很多结构均可简化为圆柱壳模型来研究,而圆柱壳是典型的轴对称结构。本工作以FGMs 圆柱壳为对象,探讨FGMs的热物理特性,建立FGMs 圆柱壳的热传导和热应力模型,分析材料参数和热环境对热传导和热应力的影响。
1 FGMs 圆柱壳建模
1.1 FGMs 模型
如图1 所示的模型为FGMs 圆柱壳单元模块,若上表面为纯陶瓷,下表面为纯金属,材料成分由两端向中面逐渐减少,在中面的陶瓷和金属所占比例相同。材料特性则由上表面纯陶瓷向下表面纯金属连续变化,如弹性模量、密度、热膨胀系数、热传导率等。但这种连续变化会受到外界环境温度以及材料体积分数影响。在图1 所示的(x,y,z)坐标系中,以中面为参考面,FGMs 在任意厚度位置的物理特性P(z)可表示为:
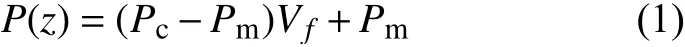
式中:P(z)是材料物理特性,如弹性模量E、泊松比ν、材料密度ρ、热膨胀系数α 和热传导系数k;Pc和Pm分别表示陶瓷和金属的材料物理属性。Vf是按设计选定的陶瓷体积分数,其表达式为:
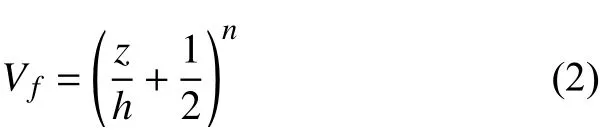
式中:h 表示FGMs 的厚度;z 是材料空间对应的坐标位置;n 是陶瓷体积分数指数,取值为0 < n < ∞。

图 1 功能梯度材料模型 (a)坐标模型;(b)成份变化Fig. 1 FGMs model (a)coordinate model;(b)composition variation
1.2 温度对FGMs 物理特性的影响
FGMs 的物理特性与环境温度有关,其表达式为:
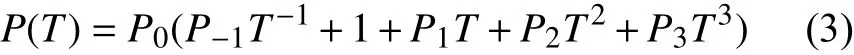
式中:P(T)代表材料的热物理特性,P0表示室温物理特性,T=T0+∆T(z)表示环境温度,室温T0= 300 K。P-1、P0、P1、P2和P3是所选材料温敏系数。ZrO2为FGMs 圆柱壳外表面陶瓷基材料,Ti-6Al-4V 为内表面金属基材料,具体系数见表1。
假设FGMs 所处环境的温度场∆T(z)仅沿着FGMs 的厚度方向变化,可得到FGMs 热物理特性模型:

式中:P0c和P0m表示室温时陶瓷和金属的物理特性。
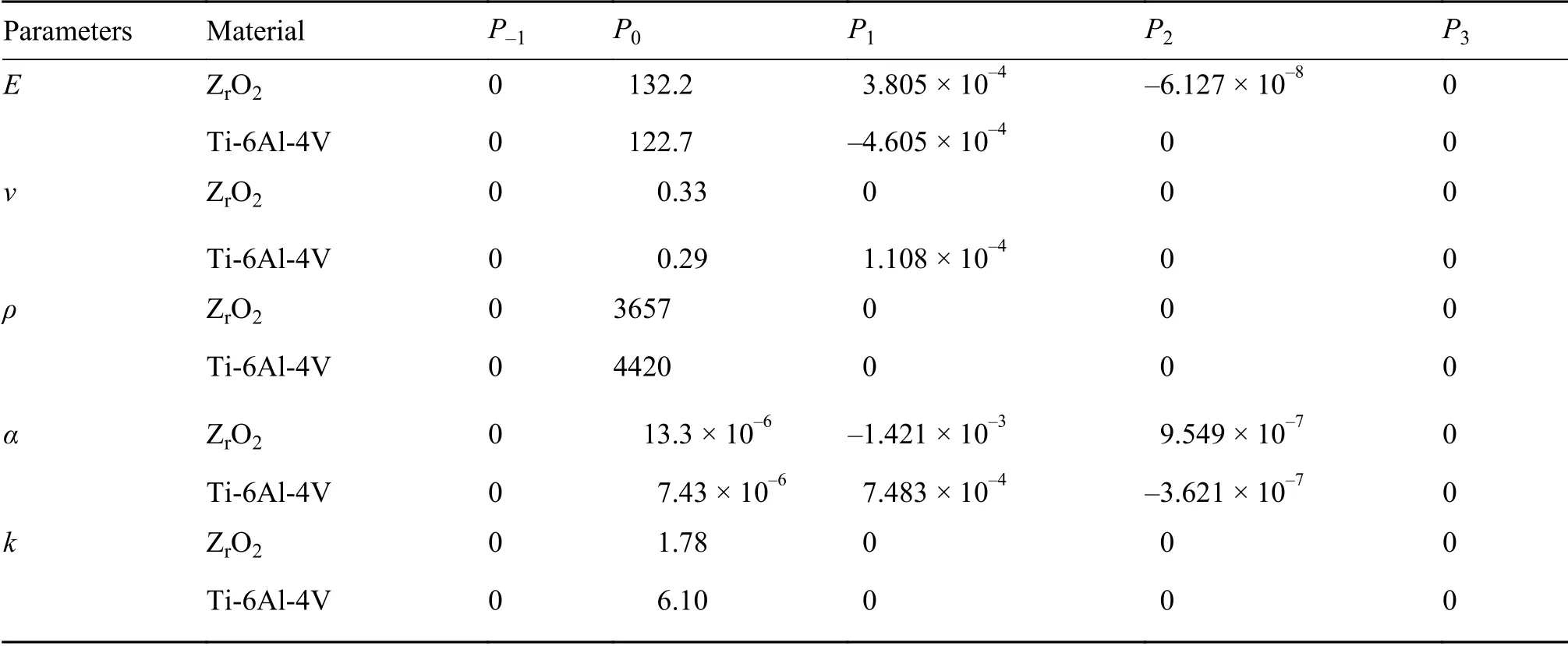
表 1 ZrO2 和Ti-6Al-4V 温敏系数[15]Table 1 Temperature dependent coefficient of ZrO2 and Ti-6Al-4V[15]
假设FGMs 处在线性温度场中,温度表达式为:
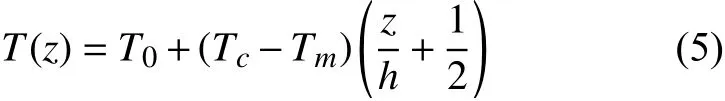
式中:Tc和Tm分别是施加在陶瓷表面和金属表面的温度,且温度是沿着厚度方向上线性升高的温度场。本工作计算分析中,取T0= 300 K, Tc= 0 K 和Tm= 1000 K。
图2 描述了室温(293 K)情况下不同陶瓷体积分数指数n 时,弹性模量E、密度ρ、热传导系数k 和热膨胀率α 沿厚度的变化。结果表明,n 一定时,陶瓷占比越大弹性模量越小,说明陶瓷弹性模量小于金属弹性模量。增大金属比重会减小FGMs的密度、热膨胀率和热传导系数。随着n 增大,FGMs 的密度、热传导系数和热膨胀率随之增大。因此,如果散热要求较高,设计时可增大陶瓷比重。

图 2 室温情况下FGMs 物理特性沿厚度变化 (a)弹性模量;(b)材料密度;(c)热传导系数;(d)热膨胀率Fig. 2 Physical properties of FGMs varying with thickness under room temperature (a)elastic modulus;(b)material density;(c)thermal conductivity;(d)thermal expansion rate

图 3 线性温度场下FGMs 物理特性沿厚度变化 (a)弹性模量;(b)材料密度;(c)热传导系数;(d)热膨胀率Fig. 3 Physical properties of FGMs varying with thickness under linear temperature field (a)elastic modulus;(b)material density;(c)thermal conductivity;(d)thermal expansion rate
图3 为n 取不同值时,线性温度场下FGMs 弹性模量E、密度ρ、热膨胀率α 和热传导系数k 沿着沿厚度的变化。结果表明,FGMs 的热传导系数和密度只和n 有关。而且,室温环境下,两者随n 值的增加而增大;线性温度场环境下,弹性模量随n 值的增加而减小。
1.3 基于Python 编程的FGMs 圆柱壳建模
将战斗机的尾喷口简化为图4 所示FGMs 圆柱壳。取FGMs 圆柱壳长L=0.8 m,中面半径R=0.405 m,壳体厚度h=0.01 m。假设圆柱壳的外表面为纯ZrO2,内表面为纯Ti-6Al-4V。材料物理特性沿厚度方向变化规律可用函数P(z)表示。利用ABAQUS 平台建立FGMs 壳的有限元模型,如图5 所示。通过Python 编程赋予不同厚度位置不同材料属性。FGMs 圆柱壳采用C3D8R 划分网格,模型总共3200 个单元。基于该模型可以分析FGMs 壳的热传导和热应力问题。
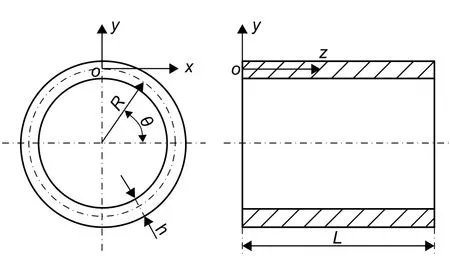
图 4 FGMs 圆柱壳几何模型Fig. 4 Geometry model of FGMs cylindrical shell
2 FGMs 圆柱壳的热应力
2.1 热应力理论
由于FGMs 圆柱壳是轴对称模型,模型内各处应力、应变和位移分量关于轴线对称。假设图5 所示FGMs 圆柱壳受到力场和热场的共同作用,则外加载荷和温度作用轴对称,且只和参数R、z 有关。

图 5 FGMs 圆柱壳有限元模型Fig. 5 Finite element model of FGMs cylindrical shell
忽略圆柱面上沿z 轴方向的剪应力和垂直于z 轴沿R 方向的剪应力。假设温度T 仅是R 的函数,建立图6 所示的圆柱坐标系,M 为圆柱壳空间的某一点。在此坐标系中:

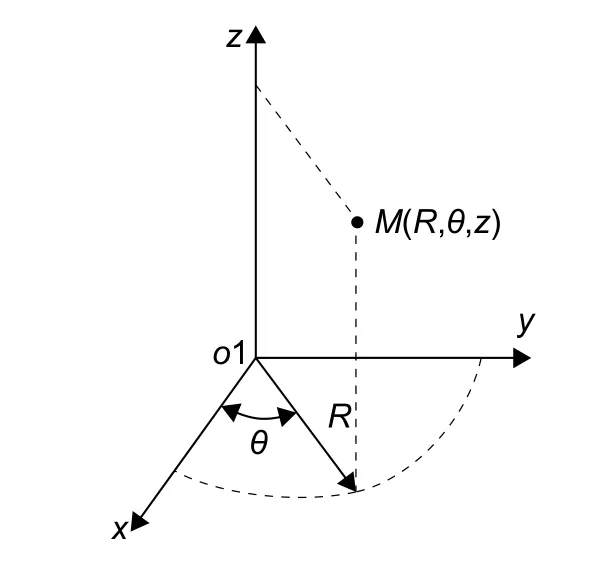
图 6 圆柱坐标系Fig. 6 Cylindrical coordinate system
不考虑外加载荷,修改空间轴对称问题的平衡方程得到FGMs 圆柱壳的平衡方程[16]:

式中:σz、σR、σθ分别为FGMs 圆柱壳的轴向正应力、径向正应力和环向正应力。
空间内一点的应变-位移关系为:

式中:u、w 分别为沿R 方向的径向位移和沿z 轴的轴向位移;εR、εθ、εz、γzR分别为径向正应变、环向正应变、轴向正应变和R 与z 方向之间的剪应变。
将关系式(8)代入圆柱坐标系的广义胡克定律得到应力-温差关系

其中:

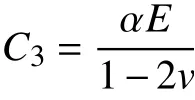
式中:E、ν、α 分别是材料的弹性模量、泊松比和热膨胀系数。
求解公式(9)可得到热应力。
2.2 热应力数值计算
战斗机在飞行过程中尾喷管表面受到强烈的气动加热,在不同的飞行空域飞行器外表面的热流密度q 不同,热应力分布复杂。取初始环境温度为20 ℃,圆柱壳的一端简支、一端自由,外表面压力为0.1 MPa。在ABAQUS 有限元软件中,选择内外表面施加热流密度q,热流密度随时间的幅值表,如表2 所示。

表 2 热流密度随时间的变化Table 2 Heat flux density varying with time
采用von-Mises 等效应力描述模型内部应力分布情况。改变q 和n 值,将自由端面厚度方向每两层应力值做平均值处理,得到每层临界面的von-Mises 应力值沿着圆柱壳厚度的变化规律,见图7和图8。结果显示,q 一定时,随着n 增加应力增加平缓。n 大于10 之后的增加幅度趋于常数,即n 不是影响应力的主要因素,因此,设计尾喷口的时候可以将n 取为10 或者10 以上。圆柱壳内层的应力小于外层的应力,因此,使用功能梯度材料设计尾喷口时,应控制应力小于材料所能承受的最大应力。n 一定时,增加q 使得材料应力增加,且q 对应力影响很大。q 达到50 kW/m2的时候,尾喷口受到的最大应力接近于材料的抗弯强度1012 MPa。为延长战斗机的飞行时长,此时应考虑其飞行空域的热流密度q。
保持q 和n 恒定时,圆柱壳的内侧和外侧应力较大,且外侧应力大于内侧应力值。n 保持一定时,q 增加应力会增大。当q 达到40 kW/m2时,最外侧应力值约450 MPa。因此,设计尾喷口时,应该考虑战斗机的飞行空域的热流密度q。q 一定时,n 大于15 的应力有突变。不同厚度位置的应力值相差较大,易出现变形的情况。设计时,减小n 可避免因变形程度不一致产生的裂纹。而在无法改变n 和q 时,改变尾喷口厚度可降低应力,但厚度必须控制在6 mm 内。当厚度大于6 mm 且n 大于15 时,需通过其他方法降低应力值。

图 7 陶瓷体积分数对不同位置热应力的影响Fig. 7 Effects of ceramic volume fraction index on thermal stress at different positions

图 8 热流密度对不同位置热应力的影响Fig. 8 Effects of heat flux density on thermal stress at different positions
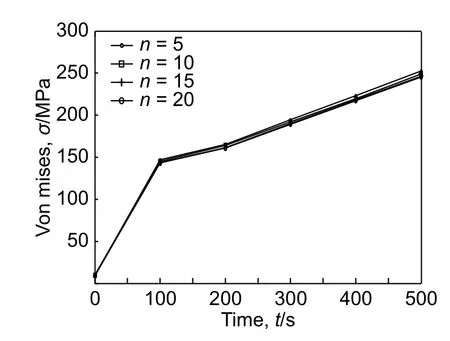
图 9 陶瓷体积分数对不同时间热应力的影响Fig. 9 Effects of ceramic volume fraction index on thermal stress at different time
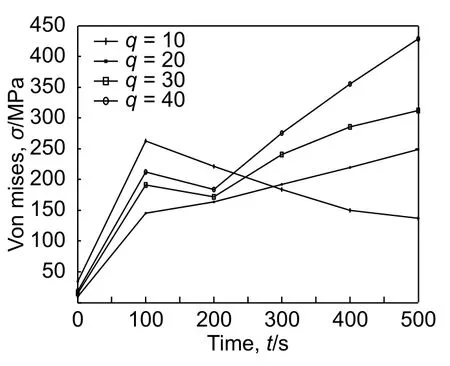
图 10 热流密度对不同时间热应力的影响Fig. 10 Effects of heat flux density on thermal stress at different time
改变q 和n 值,圆柱壳最大应力随时间变化规律见图9 和图10。q 保持一定时,最大应力值随时间增加而增加,但n 的增加对应力的增加基本无影响。尾喷口设计时,可以忽视由于n 对应力带来的影响。n 保持不变,热流密度大于10 kW/m2时,在100 s 时出现一个较大的应力值,在200 s 时出现一个较小值,之后应力开始稳定增加。热流密度小于10 kW/m2时,应力值在100 s 达到最大值,随后逐渐降低。在100 s 时最大应力值小于自由端的屈服极限,战斗机可以长时间飞行。取安全系数为2 时,如果战斗机在500 s 内未完成起飞,尾喷口的应力值还在增加时不能正常飞行。
3 FGMs 圆柱壳的热传导
3.1 热传导理论
在圆柱壳上取微单元进行热传导分析,如图11所示。

图 11 微单元热传导分析Fig. 11 Analysis on heat conduction of micro element
通过傅立叶热传导定律, 可得到x、y 和z 方向流出的净热流分别为:

式中:qx、qy和qz为单位面积上热流量,表达式分别为
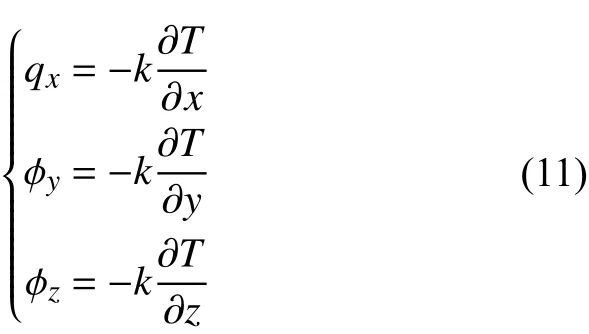
式中:T 为温度,k 为材料的热传导率。三个坐标上的净热流总和为:
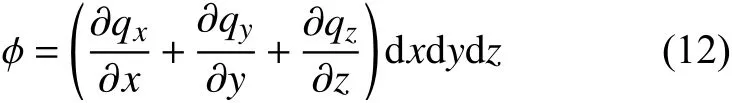
由于热传导进入微单元的净热流量和微单元本身产生的热流量都用于增大FGMs 圆柱壳的内能,因此内能W 的变化率反映了微单元内的能量随着时间的变化率:
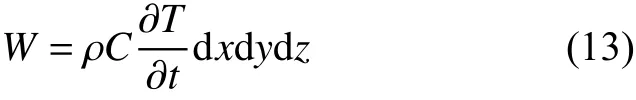
式中:t、C、ρ 分别代表时间、材料的比热和密度。
假设通过FGMs 圆柱壳的热流密度为qν,那么圆柱壳微单元的热量记为qνdxdydz。由能量守恒定律可知,热传导流入微单元的净热流和微单元内产生的热流之和与能量存储的时间变化率相等,因此:
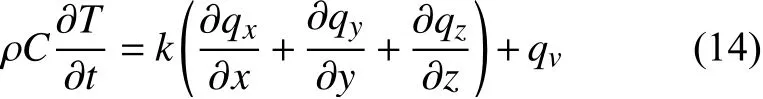
3.2 热传导数值计算
因为内热源qν随时间变化,且FGMs 圆柱壳模型壁厚较小,内热源相比外热源对热传导的影响极小,即qν= 0。假设室温下FGMs 圆柱壳的比热为c = 0.69 × 103J/(kg•℃),外热源热流密度q 从10~40 kW/m2变化。
图12 描述了热流密度q 对热传导的影响。结果表明,增大热流密度,任意截面的温度随q 值增加而升高,且q 越大,温度上升越明显。图13 表明了陶瓷体积分数对热传导的影响。结果表明,尾喷口n 变化对于任意截面温度基本上无影响。应用于设计时,假设战斗机的飞行时长设定为500 s,则飞机所处飞行空域的q 值不能超过30 kW/m2,即可根据材料能承受的最高温度和拟合函数估算出战斗机飞行时间。因此,要延长飞行时长,应选择q 较小的飞行空域。
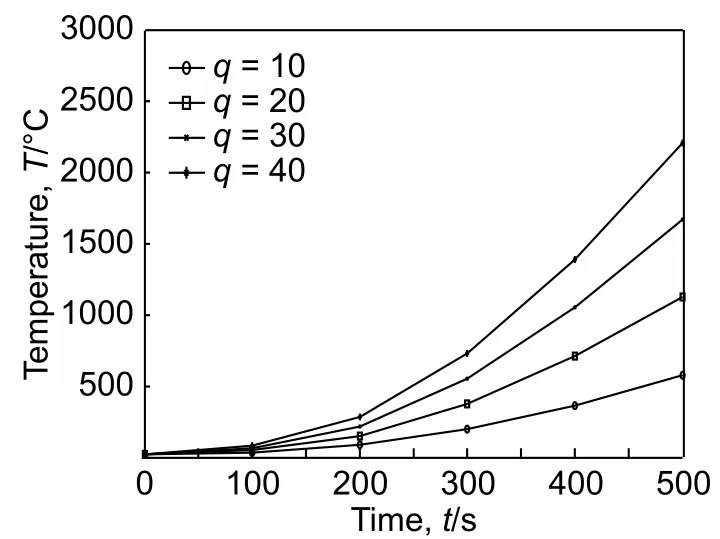
图 12 热流密度对热传导的影响Fig. 12 Effects of heat flux density on heat conduction

图 13 陶瓷体积分数对热传导的影响Fig. 13 Effects of ceramic volume fraction index on heat conduction
4 结论
(1)热流密度一定时,应力随陶瓷体积分数指数增加比较平缓,而且圆柱壳的外侧应力大于内侧应力;陶瓷体积分数指数大于10 之后的应力增加幅度趋于常数,即陶瓷体积分数指数不是影响应力的主要因素。因此,利用FGMs 设计飞机尾喷口的时候可以将陶瓷体积分数指数设计为10 以上。
陶瓷体积分数指数恒定时,应力值随热流密度的增加而增加;当热流密度等于40 kW/m2 时,FGMs 圆柱壳最外侧应力值约450 MPa,热流密度达到50 kW/m2时,圆柱壳外侧最大应力接近于材料的抗弯强度。
(3)FGMs 圆柱壳任意截面的温度随热流密度的增加而升高,而且热流密度越大,温度上升越明显,但是陶瓷体积分数变化对于任意截面温度基本上 无影响。

