筑坝堆石料抗剪强度间接测定模型与实用计算公式研究

任秋兵，李明超，杜胜利，刘承照

（水利工程仿真与安全国家重点实验室，天津大学，天津 300354）

1 研究背景

堆石料通常是指山体开采所得岩块经一定程度粉碎而得到的岩石碎块类集合体。由于其具有压实性能好、透水性强、承载力大和抗剪强度高等良好工程特性，在堆石坝等工程中得到了广泛应用[1]，作为堆石坝中堆石体填筑材料的堆石料称为筑坝堆石料（或堆石坝料）。堆石坝各分区填筑对堆石料有相应级配要求，主堆石料和次堆石料粒径相对较大，垫层料多为连续级配细石料，过渡料粒径、级配应符合垫层料与主堆石料间的反滤要求[2]。实际工程中，除要求颗粒级配和相对密度外，对筑坝堆石料的基本物理力学性能（如抗剪强度、压缩模量等）更为关注。筑坝堆石料的抗剪强度是指坝料抵抗剪切破坏的极限能力，其数值等于剪切破坏时滑动面上的剪应力。抗剪强度是衡量堆石料质量的关键指标之一，也是影响堆石坝施工进度和运行安全的主要因素，故准确测定堆石料抗剪强度一直是工程项目可行性研究以及施工建设阶段的重要任务[3-4]。随着水电工程规模日益增大，如水布垭大坝坝高达到233 m，大坝势必会遭受巨大荷载，这对作为坝体的堆石料强度特性精确、可靠描述提出了更高要求[5]。

随着现代大型施工碾压设备的普及应用，允许上坝的堆石料最大粒径高达1500 mm以上[6-7]，充分体现筑坝堆石料粒径跨度大这一特点。鉴于此，国内外学者常采用室内或原位剪切试验来直接测定堆石料抗剪强度。张其光等[8]利用新研制的堆石料风化试验仪对风化后堆石料试样进行直剪试验，探讨了风化过程中堆石料的抗剪强度特性变化；陈涛等[9]开展了冻融循环下堆石料抗剪强度试验研究，结果表明冻融循环后会使堆石料试样的抗剪强度有所降低；Liu[10]和胡伟等[11]分别研制了大型原位直剪仪，并通过测定堆石料抗剪强度验证了试验设备的工作性能。此外，若堆石料尺寸较大而试验条件难以满足要求时，则选用缩尺试验测定其抗剪强度。然而，由于缺乏合理的尺寸效应评价体系，堆石料缩尺引起的强度和变形的变化规律尚未形成统一认识，对缩尺引起的强度和变形差异的机理亦尚未完全明晰，故堆石料尺寸效应一直都是困扰工程设计和安全评价的难题[12]。孔宪京等[13-14]研发了系列三轴仪（包含国内第一台超大型静动两用三轴仪），构成了多尺度三轴试验平台，为系统研究堆石料强度与变形的尺寸效应提供了技术支撑。总体而言，常规试验仪器仅能测定中、小粒径堆石料的抗剪强度，而直接测定大粒径堆石料的抗剪强度则需通过自行研发大型试验设备来实现，导致试验成本大幅提高。再者，与常规剪切试验相比，适配大尺度试验的堆石料试样制备难度增加、时耗延长，剪切试验数据利用率却未见提升。

为了弥补上述直接测定方法（即剪切试验）的不足，作为一种有效辅助手段，堆石料抗剪强度间接测定方法应运而生。以往试验研究[15-17]表明，堆石料抗剪强度主要取决于颗粒级配、组成和密实度等[8]，且各因素与抗剪强度呈高度非线性关系[18]，这为间接测定堆石料抗剪强度奠定了坚实基础。根据理论依据的不同，现将间接测定方法大致分为数值模拟和机器学习两类。两者均是根据已有堆石料剪切试验数据对其抗剪强度进行合理推算，不仅节约了试验成本，还提高了积累试验数据利用率；有所不同的是，数值模拟注重还原堆石料试样真实性态，而机器学习则主要反映抗剪强度与其影响因素间的复杂映射关系。利用数值模拟方法重现或推断原型足尺堆石料试样的抗剪强度和变形规律较为常见[19-20]，而以机器学习为核心的数据驱动方法[21]在该方面的应用较少[6]，根据相关方法推导堆石料抗剪强度计算公式更是鲜有报道。对于现场试验员或工程师而言，数学计算公式具有简单、易用等特点，因而成为其最常运用的算术形式，而直接应用机器学习算法需要依赖开发环境和编程技能，这对筑坝堆石料抗剪强度数学模型的推广使用造成一定影响。此外，现场试验难以对公式全部自变量进行准确测试，不免会存在数据缺失或逸出等问题，这将直接影响公式推算精度。为此，有必要开发一种既符合工程应用实际情况，又能准确推算堆石料抗剪强度的鲁棒性工具。

鉴于此，本文开展基于神经网络理论的筑坝堆石料抗剪强度间接测定模型及其实用计算公式研究，其主要包括以下几个方面的内容：（1）通过广泛搜集文献资料弥补现有室内大型剪切试验数据单一和匮乏的不足；（2）针对如何从多因素中合理筛选公式自变量并确保公式推算精度这一问题，提出一种集成组合客观赋权与互信息的综合性成本型指标（comprehensive cost-type index integrating combinatorial objective weighting and mutual information，CCI）；（3）为克服神经网络易陷入局部极小值以及多参数调优复杂等局限性，耦合进化算法和误差反向传播算法形成一种神经网络混合训练方法；（4）结合神经网络拓扑结构和优化参数，将进化神经网络模型转换为实用计算公式及其简化应用方法，以促进其在实际工程中的应用；（5）利用工程实例对所提公式进行验证分析，并将抗剪强度推算值与实测值进行对比。

2 研究框架

在考虑试验数据多样性的情况下，针对筑坝堆石料自身特性提出抗剪强度实用计算公式，其研究框架如图1所示，主要包括典型试验数据库建立、公式自变量筛选、进化神经网络模型构建、公式推导与简化应用以及工程实例验证等5个步骤：（1）查阅国内外堆石料抗剪强度试验资料，收集影响堆石料抗剪强度的可量化因素及对应试验值，以建立典型室内剪切试验数据库。（2）结合相关性分析和CCI值筛选出主要因素作为模型自变量，对应因变量为抗剪强度，将归一化数据按比例拆分为训练集和测试集（即hold-out法），其中训练集用于构建遗传进化神经网络模型，而测试集则用于检验训练后模型的推算性能。（3）利用确定性系数（R2）、平均绝对百分比误差（MAPE）、平均绝对误差（MAE）和均方根误差（RMSE）等指标[22-24]量化评价进化神经网络模型于测试集上的表现。若多次性能评价均满足工程要求，表明所建模型具有初步可用性；反之，需重复步骤（1）—（3），直至模型推算精度达标。（4）根据神经网络拓扑结构和优化参数，经推导得到堆石料抗剪强度计算公式，并运用敏感性分析探寻少数关键因素，以建立一种具有鲁棒性的公式简化应用方法。（5）将所提公式应用于实际工程，通过对比验证凸显其优越性与实用性。

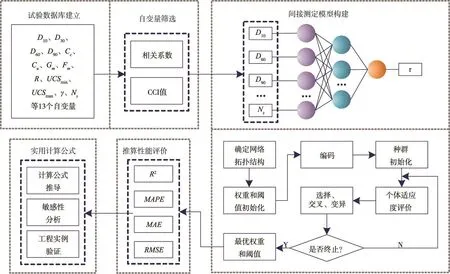
图1 研究框架

3 堆石料抗剪强度间接测定模型及实现方法

3.1 堆石料抗剪强度数学模型堆石作为一种天然材料，其工程特性受岩性、颗粒级配、岩块微裂隙、岩块强度等多种因素的影响，致使堆石料抗剪强度间接测定具有相当的复杂性。本文将基于上述复杂因素构建堆石料抗剪强度间接测定数学模型。首先，根据文献资料确定可用于计算堆石料抗剪强度的影响因素。然后，将影响因素进行分类，一类为可量化因素（如颗粒级配、岩块强度等），另一类为不可量化因素（如岩性、岩块微裂隙等）。其次，在收集国内外堆石料抗剪强度试验资料的过程中，试验数据应包含大部分可量化因素，而对于不可量化因素，则应注重试验数据的多样性和丰富性。以岩性为例，试样需源自不同岩性的堆石母岩，如砂岩、玄武岩、英安岩、花岗岩等。最后，将堆石料抗剪强度计算问题抽象为数学模型，该模型由关键因素（自变量）集、最优化拟合模型和抗剪强度计算模型等三个部分构成。

（1）关键因素集。颗粒级配（GC）、级配和细度模数（GF）、硬度和强度（RS）、相对密度（RD）和外界荷载（EL）等可量化因素共同构成关键因素集。

式中：Dn为特征粒径；g（Dn）为特征粒径的派生量；Gm、Fm分别为级配和细度模数；R、UCS分别为材料硬度和抗压强度；γ为材料密度；Ns为正应力。

（2）最优化拟合模型。将模型参数限定范围作为约束条件，构建以抗剪强度计算值与实测值的最小误差为目标函数的多元非线性拟合模型，从而达到调优参数的目的。

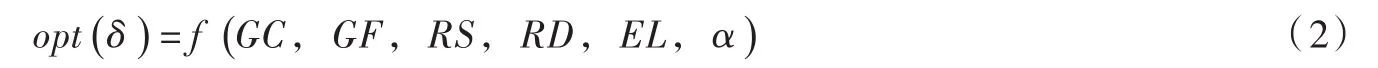
式中：δ为计算误差；α为模型参数。

（3）抗剪强度计算模型。以关键因素为输入变量，抗剪强度(τ)为输出变量，基于进化神经网络算法构建筑坝堆石料抗剪强度计算模型。

式中：enn(·)为进化神经网络算法；αbest为最优模型参数。

据此，本文将重点探讨典型试验数据库建立、自变量筛选和进化神经网络构建三部分内容，从而为推导筑坝堆石料抗剪强度实用计算公式提供必要条件。

3.2 集成客观赋权与互信息的综合性指标（CCI）模型自变量愈多，不代表模型推算精度愈高，自变量间存在高度相关关系不仅会使数学表达式复杂化，还会造成参数估计失真，故需进行自变量筛选。一般通过相关性分析剔除显著相关变量，其仅利用线性相关系数衡量变量（两自变量、自变量与因变量）间的信息重叠度，既未考虑自变量自身及其之间的固有信息，又忽略了自变量与因变量间的信息传递，故极易导致自变量筛选不当。针对上述问题，本文提出一种集成组合客观赋权与互信息的综合性成本型指标（CCI）以合理剔除显著相关变量。CRITIC（criteria importance through intercriteria correlation）法[25]可兼顾考虑各自变量间的对比强度和冲突性，并由此综合确定客观权值，但该方法未能虑及自变量间的离散性，熵权法[26]则可有效弥补这一不足。为进一步将因果关系融入变量评价准则，利用互信息法[27]改进基于CRITIC法和熵权法的组合客观赋权模型，以全面反映某个自变量在变量体系中的相对重要性。CCI值具体计算步骤如下所述。

（1）步骤1。在熵权法赋值计算中，采用q个指标对p个对象进行评价，构建判断矩阵并对该矩阵进行标准化处理。其中，xij，xij≥0为判断矩阵X中任意指标值，且其对应标准化值为由此，求得第j个自变量的信息熵值Ej和熵权值ej如下：

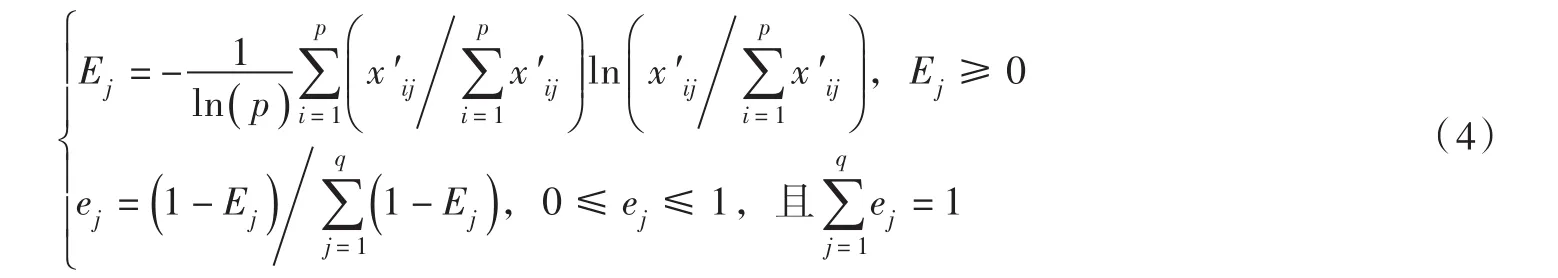
（2）步骤2。利用CRITIC法计算第j个自变量的客观权值cj。

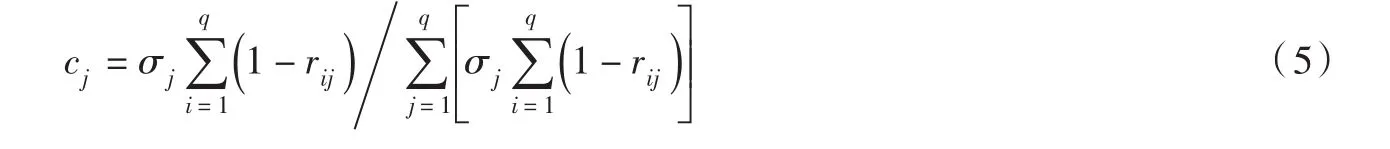
式中：rij为第i个自变量与第j个自变量之间的相关系数；σj为第j个自变量的标准差。

（3）步骤3。假设自变量xj与因变量y的联合分布为边缘分布分别为p(xj)和p(y)，互信息mj则为联合分布与边缘分布的相对熵值。

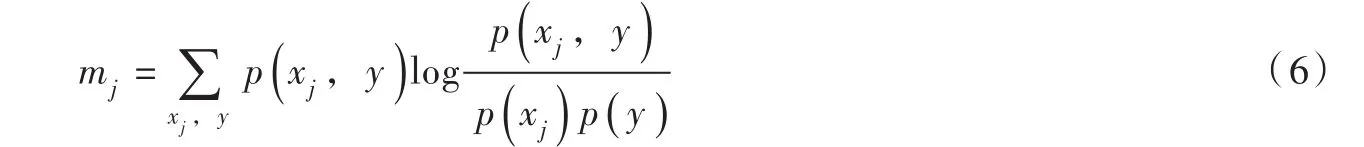
（4）步骤4。通过融合客观权值ej和cj以及熵值mj等属性求得综合性指标（即CCI值）ωj，且ωj越小，表明该指标提供的有效信息量越大，其重要程度也就越高。

式中：m为权值（或熵值）的种类个数，本文选取ej、cj和mj三种权值（或熵值），故m=3为常数；Pji为第i种权值（或熵值）的第j个计算结果；分别为第i种权值（或熵值）的最大和最小计算结果。

3.3 进化神经网络模型堆石料抗剪强度与其影响因素表现出复杂的映射关系，欲通过关键因素推算抗剪强度，亟需一种有监督的非线性回归学习算法，神经网络在这方面具有较大的优势。多层感知机是一种按照误差反向传播算法训练的多层前向型神经网络，也是目前应用较为广泛的神经网络[28-30]，其最基本成分为神经元模型（见图2）。研究表明，神经网络存在容易陷入误差函数局部极值点以及初始连接权重和阈值对推算结果影响较大等问题[31]。为此，本文采用具有全局优化性和自适应性的遗传算法[32-33]（genetic algorithm，GA）对神经网络的初始权重和阈值进行优化，以实现误差全局最小，从而构建出最优进化神经网络模型。该模型的训练过程简述如下：（1）确定神经网络拓扑结构、初始权重和阈值以及遗传算法初始参数。（2）定义适应度函数，并计算个体适应度值。（3）利用轮盘赌法进行选择和交叉操作，再进行变异操作，并重新计算个体适应度值。（4）重复（2）和（3），直至达到最大迭代次数或满足设定误差要求。（5）将适应度值最小的染色体解码得到最优初始权重和阈值。（6）运用误差反向传播算法进行局部细致搜索，当达到既定收敛精度时，结束神经网络的训练过程。

图2 M-P神经元模型

4 典型试验数据库

在3.1节中所建堆石料抗剪强度数学模型本质上是一种数据驱动的间接测定方法，即利用神经网络表达式表征大量试验数据中抗剪强度与其影响因素间的非线性映射关系，因而所用试验数据的数量和质量在很大程度上决定了公式推算精度。本文通过收集165组源自世界各地的堆石料室内剪切试验数据[34-46]（为确保试验数据的多样性，要求颗粒岩性、试样尺寸等有所区别）建立起典型数据库，将13个关键因素（包括特征粒径及其派生量、级配和细度模数等）作为公式自变量，因变量即为堆石料抗剪强度。数据库中全部变量名称、符号、单位和统计信息汇总于表1。

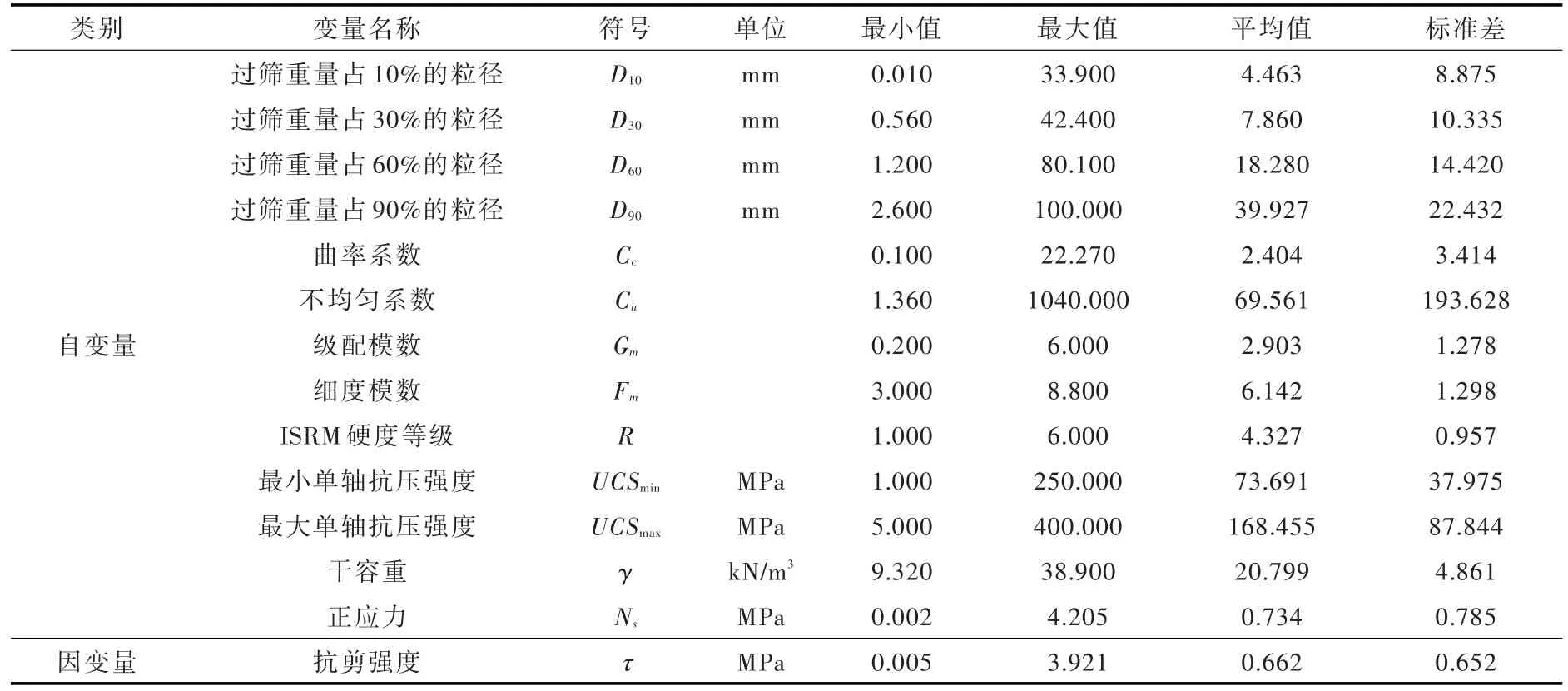
表1 试验数据统计信息

4.1 关键因素分析将影响堆石料抗剪强度特性的13个关键因素细分为堆石料级配、级配和细度模数、硬度和强度、材料密度以及正应力五类，并说明选取其作为公式自变量的缘由。

（1）堆石料级配。已有研究[47]证实，堆石料粒径级配会影响抗剪强度测定结果。不过，其具体影响规律，至今仍未有统一定论。由于原位颗粒尺寸过大，实际操作中常用级配缩尺来表征，本文亦是如此。除选用特征粒径D10、D30、D60和D90外，还加入曲率系数Cc和不均匀系数Cu两个级配派生量。

（2）级配和细度模数。细度模数Fm是表征堆石料粒径的粗细程度及类别的指标，Fm值越大，表示颗粒越粗。与Fm类似，级配模数Gm也是根据颗粒筛分结果计算而得的，Gm值越大，表示堆石料中细颗粒含量越高。

（3）硬度和强度。在高约束条件下，材料硬度会对颗粒膨胀性产生影响，采用国际岩石力学与岩石工程学会（简称ISRM）规定的硬度等级[48]R作为衡量指标。此外，增添堆石料单轴抗压强度试验数据（单轴抗压强度试验所用试件均为自然含水状态，并非饱和含水状态）中最小抗压强度值UCSmin和最大抗压强度值UCSmax作为自变量。

（4）材料密度。一般而言，堆石料抗剪强度会随着材料密度γ的增加而增加。材料密度越大，颗粒间的相互作用越显著，抗剪强度也就越大。在大尺度三轴试验过程中，通常需要控制相对密度。

（5）正应力。外界约束对堆石料抗剪强度的影响已被众多研究[49]所证明。一般认为，随着正应力Ns的增大，颗粒破碎程度得以提高，膨胀效应逐渐消散，摩擦角显著减小，抗剪强度随之降低。

4.2 自变量筛选在构建进化神经网络模型前，利用相关性分析和CCI值校核各个因素的必要性。为检验多因素间的线性相关关系，现对13个自变量进行Pearson相关性分析，分析结果以相关系数矩阵图（图3）的形式展示。由图3可知，3组变量的相关系数绝对值超过0.9，分别为D10和D30（0.97）、Gm和Fm（-0.96）以及UCSmin和UCSmax（0.94）。为减小自变量间显著相关性对公式推算精度的影响，利用3.2节方法对全部变量进行重要性评价，各变量的熵权值、CRITIC权值、互信息以及CCI值见表2。从表2可以看出，上述3组变量组内CCI值按大小排序分别为D30＞D10、Fm＞Gm和UCSmin＞UCSmax。因此，将D30、Fm和UCSmin3个冗余变量剔除，最终留存10个关键因素（包含D10、D60、D90、Cc、Cu、Gm、R、UCSmax、γ和Ns）作为公式（或模型）自变量。而后，对所有变量进行归一化处理，并将165组试验数据按8∶2的比例随机拆分为训练集和测试集，其中132组数据用来训练进化神经网络模型，剩余33组数据则用于评估其推算性能。

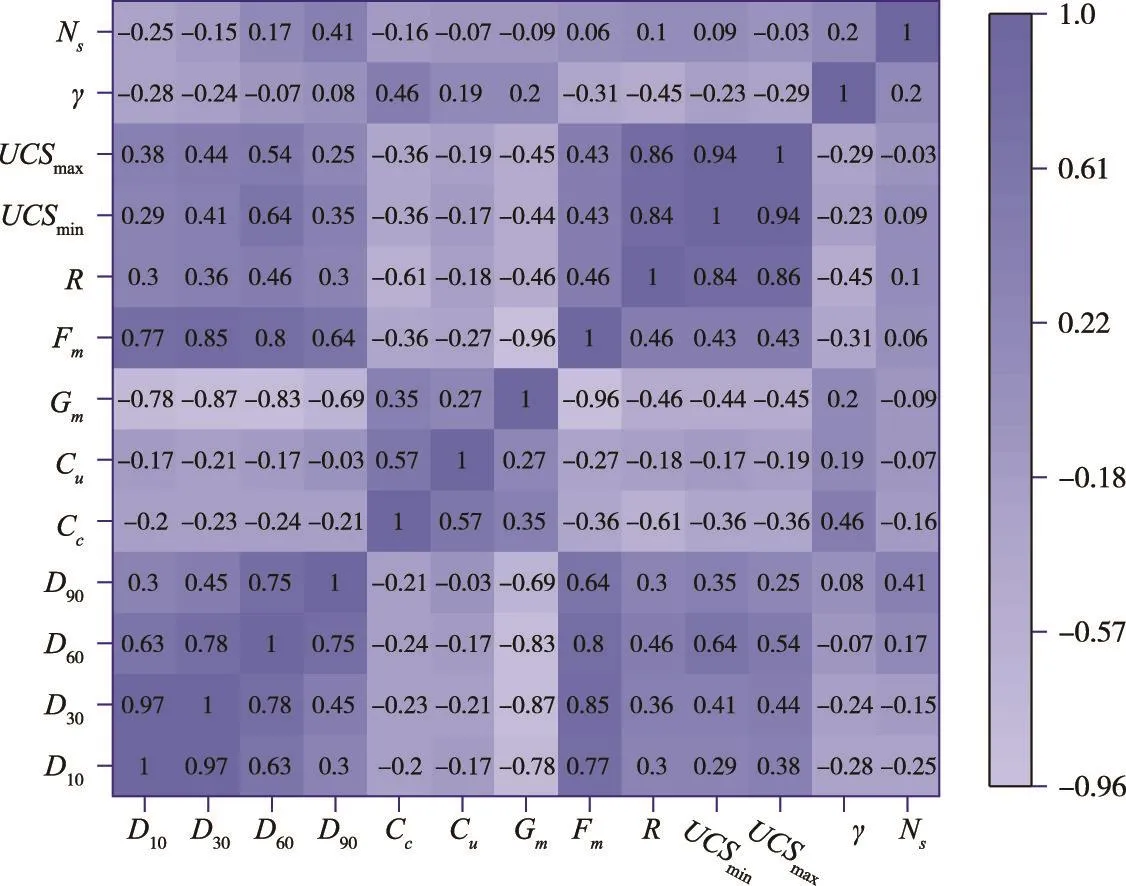
图3 Pearson相关性分析结果

表2 各变量的熵权值、CRITIC权值、互信息和CCI值

5 堆石料抗剪强度实用计算公式推导

5.1 模型拓扑结构确定当确定自变量和训练集后，输入层和输出层节点数随之固定，此时首要问题转变为如何优化隐含层数和隐含层节点数。理论上已经证明，具有一个隐含层的三层神经网络可以逼近任意非线性函数[50]，故优先考虑单隐含层神经网络。一般认为，隐含层节点数过少，难以拟合复杂映射关系；反之，网络训练时间增加，且容易出现“过拟合”现象。本文采用试凑法优化隐含层节点数，先根据经验公式[51]选定隐含层节点数范围为3≤L≤20，L∈ℤ，后在该范围内逐步增加节点数以寻求对应最佳拟合效果的节点数。具体来说，对每个既定节点数分别进行10次训练，同时保存训练、测试和总体R2值，剔除对应最小和次小R2值的推算结果，取剩余8次结果求平均R2值，并将其记录于图4中。由图可知，当隐含层数为5、9、11、15和20时，3种R2值均为98%左右。依据“在满足精度要求的前提下取尽可能紧凑的结构，即取尽可能少的隐含层节点数”这一原则，最终确定隐含层节点数为5，即单隐含层神经网络结构为10-5-1。

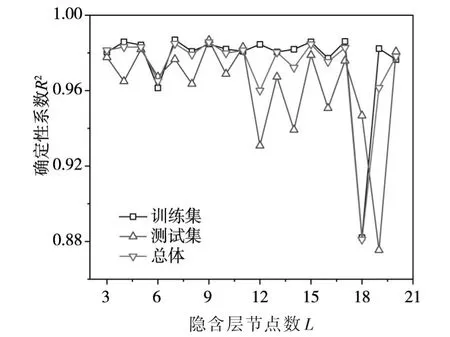
图4 确定性系数与隐含层节点数的关系

图5 平均适应度曲线

5.2 进化神经网络模型构建根据5.1节神经网络拓扑结构，设置遗传算法初始参数：最大进化代数取100，种群个数取50，交叉概率和变异概率的取值分别为0.3和0.1，染色体长度取(1 0+1)×5+(5 +1)×1=61，并将适应度函数定义为其中M为训练样本数，yi和分别为训练样本中第i个实测值和对应推算值。此外，设定神经网络最大训练次数、学习率和训练要求精度分别为100、0.1和0.000 01，其训练方法则采用Levenberg-Marquardt算法[52]。利用遗传算法优化神经网络初始权重和阈值，平均适应度曲线见图5。由图5可知，学习过程收敛速度较快，大约经过25次进化即可寻得最优解，此时平均适应度趋近平稳。将优化所得权重和阈值赋予对应网络参数，并采用误差反向传播算法继续训练网络。训练过程彻底结束后，利用测试样本评估进化神经网络模型，以凸显其良好推算性能。

对全部数据进行反归一化处理，并将训练集和测试集中实测值与推算值线性拟合效果绘制于图6中。从图中6可以看出，模型训练和测试R2值均大于0.9，且两者差距较小。此外，对于少数抗剪强度大于1.5 MPa的数据点（仅占总数据量的10%左右），模型训练和测试效果亦较佳，可见所建模型具有较好的泛化能力。为准确描述所得模型性能，采用统计指标对推算结果进行量化评价，评价结果见表3。由表3可知，模型训练和测试效果较为接近，说明模型推算未出现“过/欠拟合”现象。

图6 堆石料抗剪强度实测值与推算值线性拟合关系

5.3 计算公式推导将5.2节中进化神经网络模型拓扑结构绘制于图7中，网络隐含层和输出层传递函数分别采用双曲正切Sigmoid函数（用tansig(·)表示）和线性函数（用purelin(·)表示），各层阈值和层间连接权重汇总于表4。为确保进化神经网络模型公式化的同时不降低其推算精度，结合图7，根据神经网络理论[53]推导得到如下神经网络数学表达式：

式中：Ok=16为因变量堆石料抗剪强度；Ii为第i个自变量；ftansig、fpurelin分别为隐含层和输出层的传递函数；θj、θk分别为第j个隐含层节点和第k个输出层节点的阈值；wij、wjk分别为第i个输入层节点与第j个隐含层节点之间的连接权重和第j个隐含层节点与第k个输出层节点之间的连接权重。

表3 模型性能量化评价

表4 进化神经网络模型各层阈值和层间连接权重

图7 进化神经网络模型结构

为便于工程应用，特将式（10）变换为：

通过提取网络连接权重和阈值（见表4）并将其代入式（11），即可获得拓扑结构为10-5-1的单隐含层进化神经网络模型的对应表达式，即筑坝堆石料抗剪强度实用计算公式：

需要注意的是，使用式（12）需对全部数据进行归一化与反归一化操作。

5.4 实用公式简化相较于进化神经网络模型，堆石料抗剪强度实用计算公式应用更为方便，且推算精度相仿。然而，工程现场试验数据繁杂，容易出现数据缺失或逸出等情况，故完成多达10种堆石料特性（自变量）的准确测定难度较高，如何减少自变量个数同时避免推算精度下降较大便成为工程应用中亟待解决的问题。为此，通过敏感性分析量化各个变量影响堆石料抗剪强度的显著程度，提出一种堆石料抗剪强度实用计算公式简化应用方法。

堆石料抗剪强度计算公式是由神经网络模型推导而得的，为使敏感性分析结果更为可靠，需寻求一种与神经网络训练过程密切相关的多因素敏感性分析方法。由5.2节可知，不断调整的连接权重大小可反映自变量对因变量的影响程度，确定输入层至输出层间的权重分布情况，即可确定各个自变量的主次关系。改进Garson算法[54]是基于网络连接权重的敏感性分析方法的一个代表，其利用连接权重的乘积计算各个自变量对因变量的贡献值sik，公式如下：

式中：N为输入层节点数；L为隐含层节点数；k=1，2，…，M，其中M为输出层节点数；sik为自变量对因变量的敏感度表征，sik值越大，敏感性越显著。

结合表4中进化神经网络模型层间连接权重，利用改进Garson算法对全部自变量进行敏感性分析，结果如图8所示。由图8可知，在影响堆石料抗剪强度的10个关键因素中，Ns、D10和D90最为显著，Cu、Gm、R和UCSmax次之，D60、Cc和γ最小。sik值排序前6的自变量的贡献率大于0.8，故选取Ns、D10、D90、Cu、Gm和R作为简化公式（或模型）的自变量。遵照5.1节所述方法，确定简化单隐含层神经网络模型拓扑结构为6-2-1。依据5.2节建模流程，构建出简化神经网络模型，其各层阈值和层间连接权重见表5，推算性能量化评价结果见表6。对比表3和表6可以看出，各项统计指标差距较小，说明删减自变量后的简化神经网络模型推算性能仍与原模型相近。

根据5.3节推导步骤，将表5中数据代入式（11），即可获得筑坝堆石料抗剪强度简化计算公式：

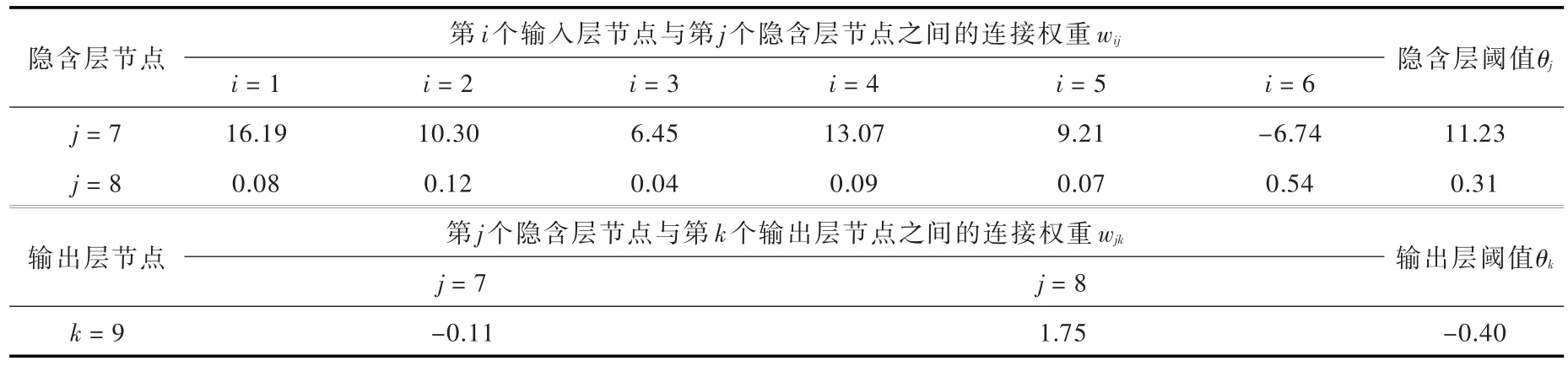
表5 简化神经网络模型各层阈值和层间连接权重

表6 简化模型性能量化评价

表7 工程试验数据汇总

6 工程实例验证

基于上述推导结果，以独立于训练集的工程实测数据为例，对式（12）和式（14）进行稳定性和准确性验证，旨在通过此实例说明所提计算公式及其简化应用方法在堆石料抗剪强度推算方面的优

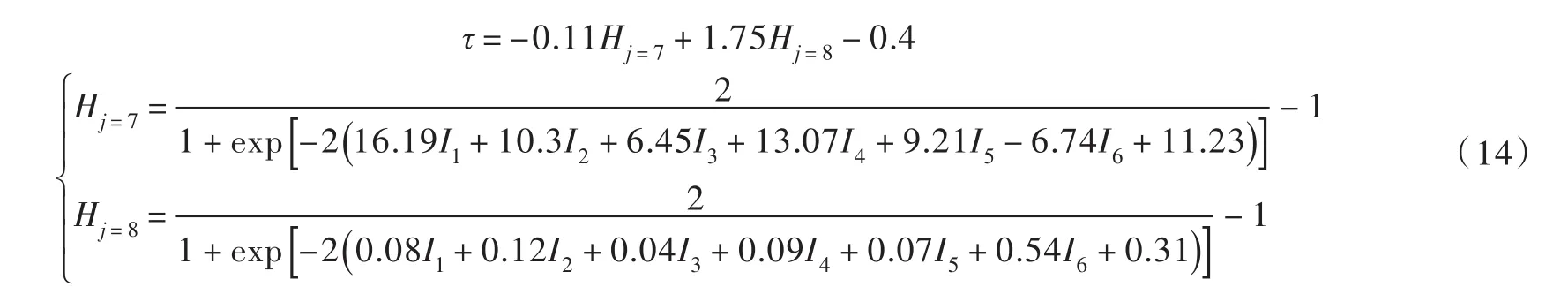
图8 敏感性分析结果

6.2 准确性验证基于6.1节所述仿真试验，利用R2、MAPE、MAE和RMSE等统计指标对10次推算结果分别进行准确性量化评估，并将每个指标的10次计算结果取平均数作为最终评判标准，其结果示于图9中。由图9可知，两公式对应4个指标数值点围成的图形的重叠区域较大，说明两公式对9组试验测得抗剪强度的总体推算精度大致相当。与稳定性验证结果类似，式（12）的推算准确性亦较佳。综上，实际工程应用中，倘若试验条件相对完备，获取堆石料特性信息较多，建议使用式（12）推算试样抗剪强度；反之，则推荐选用所需材料特性信息较少的式（14）对试样抗剪强度进行估算。

表8 公式推算稳定性量化评价结果

图9 式（12）与式（14）推算准确性对比结果

7 结论

本文基于进化神经网络算法提出了一种筑坝堆石料抗剪强度实用计算公式及其简化应用方法，所提公式可利用D10、D60、D90、Cc、Cu、Gm、R、UCSmax、γ和Ns等10个关键因素准确推算堆石料抗剪强度，具有较好的实用价值。本文主要研究结论总结如下：（1）堆石料抗剪强度试验数据的多样性是开发数学模型的基础，建立典型室内试验数据库有助于构建适用范围较广的筑坝堆石料抗剪强度实用计算公式。（2）利用Pearson相关系数和CCI值对多因素进行相关性和冗余性校核，以此达到合理势。为探讨某工程所用堆石料的抗剪强度特性，Indraratna等[55]选用当地玄武岩制备诸多试样进行室内大型三轴压缩试验，部分试样特性及其试验结果汇总于表7。

6.1 稳定性验证神经网络初始权重和阈值的随机性导致式（12）和式（14）每次计算结果不尽相同，因此有必要对所提公式的稳定性进行验证。现将各自所需变量数值（见表7）代入式（12）和式（14），两者分别进行10次推算，并采用标准差和变异系数评价9组试验对应抗剪强度推算结果的离散程度，量化评价结果见表8。从表8可以看出，两公式对每组试验测得抗剪强度的多次推算结果波动均较小，通过对比分析进一步表明具有更多自变量的式（12）的稳定性表现更为突出。剔除显著相关变量的目的。（3）所提公式在测试样本和工程实例中推算性能较为突出，表明神经网络可以充分逼近堆石料抗剪强度与其影响因素间的复杂非线性关系，且遗传算法能够有效优化神经网络初始连接权重和阈值。（4）改进Garson算法能够合理量化各个因素对堆石料抗剪强度的敏感程度，对解决测试数据缺失或逸出等实际问题起到一定的帮助作用。（5）实用计算公式及其简化应用方法易于实现手工计算和电子表格自动运算，为推算筑坝堆石料抗剪强度提供了一种简便工具，从而能够促进其在实际工程中的应用和发展。

此外，开发该实用公式的主要目的是为了提高积累试验数据利用率和减少部分重复性测试工作，并非完全取代室内或原位剪切试验。目前该方法还存在大粒径堆石料试验数据资料较少、公式自变量代表性不足、公式推导未考虑区分软硬岩等方面的问题。鉴于这类机器学习方法的优势在于大数据分析，后续将结合更多室内试验数据和实际工程应用开展进一步研究与提升。