常闭式电磁制动器驱动结构设计及性能分析

李孝坤 董 芳 许宝玉

(1.郑州铁路职业技术学院 机车车辆学院，河南郑州 450000；2.郑州铁路职业技术学院 继续教育学院，河南郑州 450000；3.河南理工大学 直驱电梯产业技术研究院，河南焦作 454000)

1 引 言

常闭式电磁制动器具有制动力大、响应快、环境适应性强等优点，广泛应用在提升系统、工业自动化等领域[1]。张尊睦等人通过改变制动器启、停时励磁线圈的电压来降低高耗能的缺点[2]，但并未对其结构进行设计；寇宝泉等人提出了一种新型串联磁路混合励磁直线涡流制动器结构方案[3]，推导出了其解析模型；郭俊豪等人设计的随动直线式制动器[4]适用于直驱电梯制动系统，并对制动器的驱动结构进行了优化；张振川[5]等人设计的可快速分闸、具有混合励磁结构的新型电磁制动器，减小了响应时间。结合以上新型电磁制动器的设计理念，以降低能耗及实现制动器轻量化为设计目标，将永磁体引入到常闭式电磁制动器驱动结构中，利用电磁与永磁磁通量相互耦合的原理，设计出了磁路合理、大推力密度的新型电磁驱动结构。

2 新型电磁驱动结构工作原理

图1 电磁驱动结构简图Fig.1 The structural diagram of electromagnetic drive mechanism

新型电磁驱动结构简图如图1所示。钕铁硼永磁体镶嵌在铁心之间，极性如图1中所示；左、右动子通过动子连接板集成一体，相对定子部分(铁心、永磁体及线圈组成)可实现左右往复运动，右动子与制动弹簧相接，左动子外接制动臂，线圈1与线圈2并列缠绕在铁心上且两线圈反向串接。制动器处于制动状态时电磁驱动结构中左动子与定子间的气隙为9mm(右动子与定子间的气隙为1mm)，永磁体对右动子的吸力与弹簧的回复力两者的合力通过动子连接板施加到左动子上，施力载体左动子将制动力作用到制动臂上。

制动解除时电磁驱动结构中磁通量分布如图2所示，永磁体的磁通φ5抑制两串接线圈的磁通φ0，避免在定子内部形成闭合磁回路，使磁通量φ0尽可能多的穿过左动子(磁通量φ6可忽略)，耦合后的磁通量对其产生较大磁吸力，左动子在吸力的作用下推动右动子压缩弹簧克服其提供的制动力；而处于打开维持状态时(左动子与定子间气隙为1mm)，由较小电流励磁出的磁通量φ01和永磁体磁通叠加后对左动子的吸力即可克服弹簧的回复力。

图2 电磁驱动结构磁通量分布图Fig.2 The magnetic flux distribution diagram of electromagnetic drive mechanism

3 新型电磁驱动结构技术参数的确定

参照铁磁材料磁化曲线及钕铁硼最大磁能BH=314kJ/m3，结合永磁体工作在最佳磁能积点时磁能(Fm=Hchm/2)，初步确定电磁驱动结构中永磁体尺寸为80mm×100mm×18mm。

稀土永磁材料(钕铁硼)热稳定性较差，温度过高磁能积降低，磁性能将发生不可逆变化[6-10]；电磁驱动结构中通电线圈通过热辐射对永磁体磁稳定性产生一定影响，故线圈最大温升值须控制在退磁温度以下。

两线圈并列缠绕在铁芯上，匝数可由式(1)确定

(1)

式中：SAn——线圈槽面积；I——解除制动时通入励磁线圈的电流；Kf——槽满率(0.6～0.85)；jrx为容许电流密度(短时工作制，jrx=(13～30)A/mm2)。

其中，取

Kf=0.65，jrx=23A/mm2，I=38A，SAn=460mm2

计算可得

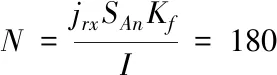
单根铜导线直径为

(2)

式中：qdx——单根导线截面积。

参照圆截面电磁线线径及其绝缘层的厚度标准，取导线直径ddx=1.45mm，相应绝缘层的厚度为0.04mm。

电磁驱动结构通入2A维持电流，线圈理论温升值参照电磁铁发热公式确定

(3)

式中：ρx——导线电阻系数，ρx=0.0219Ω·mm2/m(80℃)；p——接通时间百分比，p=HB%=1；μm——线圈散热系数(μm=(9.5～12.7)W/m2·℃)；fk——填充系数；bxq——线圈宽度(bxq=12mm)；l——线圈长度；IN——线圈安匝数(IN=360安匝)；

其中，fk，l理论值可由式(4)确定

(4)

式中：k——经验系数，取k=0.83；d1——漆包线直径(d1=1.49mm)；Qd——导线总截面积，mm2；Qx——线圈横截面积，mm2。

影响线圈温升值的各参量确定后，θ的理论计算值为14.2℃，在散热条件良好的情况下，线圈表面温度热传递较快，可认为线圈散发的热量基本正比于线圈的温升，永磁体磁性能稳定，电磁驱动结构工作稳定。

基于理论计算确定电磁驱动结构的主要技术参数见表1。

表1 励磁线圈基本参数Tab.1 The basic parameters of excitation coil参数数值N/匝180I/A38I0/A2ddx/mm1.45SAn/mm2460θ/℃14.2

4 新型电磁驱动结构静态特性分析

4.1 电磁驱动结构模型及磁通量

赋予电磁驱动结构各部件相关材料，经拉伸形成三维实体模型，为防止空气对磁场造成影响以确保有限元分析结果的准确性，在驱动结构周围建立了空气包。采用四面体单元离散模型，气隙处的剖分精度相对较高，处理后的有限元模型如图3所示。

图3 电磁驱动结构有限元模型Fig.3 The finite element model of electromagnetic drive mechanism

励磁线圈在两不同值电流(38A，2A)激励下，电磁驱动结构内部磁通量分布如图4所示。

图4 电磁驱动结构磁通量分布矢量图Fig.4 The magnetic flux distribution vector chart of electromagnetic drive mechanism

由图4可见，电磁驱动结构在38A电流激励下，永磁体磁通与线圈励磁出的磁通相互耦合，叠加后的磁通量经过左动子并对其产生3 541N吸力，磁路中饱和磁感应强度低于2.158T，材料导磁率高；线圈通入2A直流电励磁出的磁通量与永磁体磁通量耦合后在磁路中分布更合理且饱和磁感应强度降低。

4.2 电磁驱动结构静态特性分析

永磁体的引入增加了电磁驱动结构的推力密度，在同等条件下，为使引入的永磁体更合理，以电磁驱动结构对动子产生的吸力为评价指标，重点分析永磁体形状对磁路的影响。与L形永磁体等永磁量的T、反T形两种结构如图5所示，励磁线圈在2A电流激励下的磁通量分布。

图5 T型永磁体电磁驱动结构磁通量矢量图Fig.5 The magnetic flux vector of electromagnetic drive mechanism with T permanent magnets

由图5可看出，两相似形状的永磁体产生的磁通均与线圈励磁出的磁通较好的耦合，但反T型电磁驱动结构磁路中饱和磁感应强度高于L、T型，相较导磁率降低。以工作维持电流I(A)为横坐标，电磁吸力F(N)为纵坐标，绘制驱动结构对左动子的电磁吸力曲线，如图6所示。

从图6可知，电磁驱动结构对左动子的吸力随工作电流的增加而变大，含L形永磁体的电磁驱动结构对左动子的吸力大于T形及反T形，而含反T形永磁体的电磁驱动结构产生的电磁吸力最小，仅为含L型永磁体的0.94倍(4 790N)。与传统电磁驱动结构相比线圈体积缩减1/2使电流大幅度减小，降低了能耗。

图6 电磁吸力随电流变化曲线图Fig.6 The change curves of electromagnetic force accompanied with current

永磁量的增加理论上应能够提供更大的电磁力，与L形永磁体相比，U形、H形、反对成形、反U形永磁体较之永磁材料有所增加，将增加材料后的永磁体替换L形永磁体，励磁线圈通入维持电流后，电磁驱动结构磁通量矢量图如图7所示。

图7 不同型式的电磁驱动结构磁通量矢量图Fig.7 The magnetic flux vector of electromagnetic drive mechanism with different shapes permanent magnets

由磁通量矢量图7可看出，电磁驱动结构产生的绝大部分磁通量均能在定子与左动子间形成封闭磁回路，有少量磁通经过右动子，且磁路中最大磁感应强度均小于材料饱和磁感应强度。从磁路中最大磁感应强度角度分析，含反U形永磁体的电磁驱动结构最小，材料的导磁效率最高，含U形永磁体的驱动结构次之，含反对称形永磁体的结构略低于U型，相比，含H形永磁体的驱动结构磁感应强度最大，材料的导磁率最低，由其构成的电磁制动器在性能上最差;而对左动子的电磁吸力曲线如图8所示。

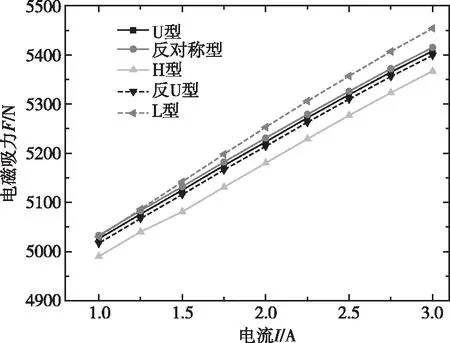
图8 不同型式的电磁驱动部电磁吸力随电流变化曲线图Fig.8 The change curves of electromagnetic force accompanied with current

由图8可以看出，含L形永磁体的电磁驱动结构对左动子产生的电磁吸力高于U、H、反U、反对称形；含U、反对称、反U形永磁体的驱动结构产生的吸力相差不大，相比含H形永磁体的驱动结构产生的电磁吸力最小。

关于永磁体的结构形式对电磁力的影响已做了探讨分析，并且得出了相对较理想的永磁体形状，除此之外，励磁线圈电流、动定子间气隙等因素对电磁力也有所影响；以电磁制动器解除制动至通电维持状态为研究对象，分析变电流、变气隙工况下左、右动子所受电磁吸力变化情况，基于非线性拟合获得电磁吸力三维曲线图，如图9所示，其中X轴数值表示励磁线圈电流I(A)的大小，Y轴数值表示位移S(mm)量，Z轴数值表示电磁吸力F(N)的大小。

由图9可以看出，电磁驱动结构对左动子的电磁吸力随励磁电流的变大及位移的减小而增加，相反，电磁吸力减小；左动子在小位移大电流工况下电磁吸力增幅较大，而右动子处于相同状态时其所受电磁吸力增幅趋于零，总体上来看，左动子受到的电磁吸力增幅较右动子平缓，右动力所受电磁力衰减幅度较大。

图9 随气隙、电流变化的静态电磁吸力示意图Fig.9 Static electromagnetic force that varies with the current and air

5 结束语

本文将永磁体引入到电磁制动器驱动结构中提出了一种新型电永磁驱动结构。采用有限元法分析了其内部磁通量的变化，电磁与永磁的磁通量耦合程度高且磁路较合理。通过对比分析不同形状的永磁体对电磁吸力的影响，得出含L形永磁体的电磁驱动结构产生的电磁吸力最大，磁路中最大磁感应强度值较小，材料导磁率高。变气隙、变电流工况下动子所受电磁吸力增长率低，避免了振动、冲击，保证了系统的稳定性。此外，永磁体的存在降低了线圈能耗，且新型电磁驱动结构的设计思路对大推力密度、轻量化的制动器及作动器设计研发具有一定的参考价值。