基于混沌蚁群的自适应路由优化算法

李方宇，张 岩

(1.安徽理工大学 计算机科学与工程学院，安徽 淮南 232001；2.阜阳师范大学 计算机与信息工程学院，安徽 阜阳 236037)

无线传感器网络WSN(wireless sensor network)凭借自组织、低成本和长周期等特性被广泛的应用于地质勘测、军事等不同领域。由于网络中节点数量有限，节点间的通信需要经过多跳方式进行，故选择范围内最优域。但因传感器能量受限，网络路由拓扑将正向影响节点可用性甚至无线传感器网络的生命周期。因此，如何在有限的能量资源内进行路由优化和降低网络能耗，从而延长整体网络的生命周期是该领域研究的重点[1-2]。

1 相关工作

目前，虽然传统网络环境下的路由优化算法取得了令人满意的成果,但先就实验初始值方面,大多数基于小范围区域或固定节点进行实验,在算法的计算复杂度较低且不具有一般性;其次就无线传感器网络的特性方面,现在的传统方法难以有效解决NP难问题。文献[3]提出了一种模式转化情况下的数据包发送策略,结合遗传算法和细菌觅食算法构建最优路径；文献[4]将网络生存周期和路由健壮性作为优化目标,选择最优适应值集中的节点构成路由拓扑；文献[5]设计一个兼顾网络能耗和能量均衡度的通信代价模型,以构建簇间路由树；文献[6-8]同时考虑了能耗均衡和蚁群信息素浓度,提出了一种利用单跳传输方式确定下一跳节点的方法,但此方法未考虑节点间传输时延等问题；文献[9]采用了以节点通信半径为依据,将网络进行虚拟网格化,从而提出一种综合能耗和传输时延的路由构建方案；文献[10]通过引入混沌蚁群算法使其发挥自组织性及动态寻优等特点使得节点间处于最优,有效减少局部和全局路径的长度,减缓网络能量消耗速度；文献[11]提出以圆环为单位的划分策略,通过对蚂蚁多次位置交换的手段构建出能量消耗较为均衡的网络。

本文基于混沌蚁群算法CAS（chaotic ant system）模型,引入蚂蚁势及熵因子,依次应用在更新传输跳转概论和传统混沌蚁群模型中。新的混沌蚁群优化算法在采用区域划分方法的基础上取代了簇的划分，首先在跳转概率最大扇环内寻找邻居蚂蚁，并与蚂蚁进行多次位置择优，确定最优蚂蚁位置并成集；最后依据最优节点机生成全局路由拓扑。整个算法减少了算法计算量的同时,增强蚂蚁之间的感知能力，提升了其群体的局部搜索能力和求解精度，有效的减少了路由拓扑长度,均衡网络能耗，从而降低因节点间通信距离的能耗，达到延长无线传感器网络的生命周期的目的。

2 问题描述

2.1 WSN自适应路由优化问题

考虑到一个无线传感器网络由一定数量的异构传感器组成，由有限条数据通路构成网络拓扑，假定在该网络中存在一个固定的Sink节点，即在一定的监控区域中所有传感器产生的数据信息通过有限条数据通路进行传递至Sink节点，则自适应路由优化的目标就是要大幅度缩减有限条数据通路的数量，在尽可能满足适应值最优的前提下，降低网络能耗，缩短路由拓扑长度，达到以延长网络生命周期的目的。

2.1.1 网络能耗模型

根据文献[12]提出的能耗模型，文本重点考虑主体通信能耗，并设定忽略其他因素对能耗的影响。即传感器节点n的通信能耗En为

其中：Er与Es分别为传感器节点n发送、接收数据所消耗的能量；Eelec为每比特数据被发送的能耗；εfs为比例系数；D为矢量距离。

2.1.2 传输能量区域划分规则

根据实际需求，本文提出一种传输能量区域划分规则，取代了传统的簇头选择及成簇的环节，通过计算其跳转概率选举出相交或相邻同心圆范围中最优适应值的某一扇环作为下一跳节点的备选区域，有效保持最优节点集精度并减少其计算量。设定等宽rseg为划分单位，将节点n的最大传输半径rn划分成k个以n为圆心的同心圆环，其中k=rn/rseg。考虑到节点n的传输代价与扇环位置呈正相关等现象，设定内围扇环节点与n采用单跳传输，外围扇环选择环中适应值最优节点作为中继节点。根据跳转概率可得出在扇环q1和扇环qk中必然存在的性能达到最理想效果的扇环qbest，该扇环中的节点不仅满足了适应值最优，同时当该扇环某一节点失效时，也可以选择该扇环内适应值次优节点作为替代。上述传输能量区域划分模型如图1所示。

图1 传输能量区域划分

2.1.3 跳转概率

以文献[13]的向前区域划分为基础，假设扇环qu向下一个扇环发送数据的概率为pu，则数据在第u扇环区域传输概率为yu，即

其中：yu=pu+1yu+1+λu,u=1,…,k。

令pk=0，即可得

其中：λ=yu/s1e1,eu=Eu/su，λu为节点适应值最优事件在第u扇环区域发生的概率且与第u扇环区域面积呈正比，su为扇环内面积，Eu为su内节点的总能量。跳转概率pu越大，即节点最优事件发生的概率越大，其扇环内节点自适应值较优。

式(4)表示扇环qu是否满足跳转概率最优，若Mqu=0，则表示扇环跳转概率最优。

2.2 混沌蚁群自适应模型的构造

混沌蚁群算法作为一种解决内在结构一致的非线性问题的方法，其遍历性、自适应性和动态寻优等特点是构建网络最优路径的主要方式。但考虑到传统混沌蚁群算法中蚂蚁与其邻居蚂蚁之间正影响力不足等问题，本文设计了一种基于势的混沌蚁群优化模型。结合蚂蚁i与其邻居j周边影响因子，根据其影响强度对节点赋予不同的势。将其运用于传感器网络节点自适应路由中，不仅增加蚂蚁个体的感知能力，同时也增强了蚂蚁与范围内节点的交互程度，即蚂蚁群体具备更强的寻优能力从而减少局部最优解的发生概率。

假设蚂蚁i与j分别位于(xi,yi)与(xj,yj)处，且蚂蚁j为蚂蚁i的邻居，则蚂蚁i与蚂蚁j之间作用的势为

其中：Ni为蚂蚁i邻居所处扇环内节点个数；w为距离因子且与节点通信范围呈正比；ρ为缩小常量，ρ=0.05。蚂蚁i对蚂蚁j作用的势反映了两者的矢量距离、蚂蚁j所处的扇环内节点个数与密度等情况，蚂蚁i的邻域节点密度也将作用其最优位置的更新，即与下一跳可选节点的个数呈同一趋势，从而扩大择优范围，寻到全局最优解，则基于势的跳转概率由式(3)演变为

本文提出的路由平衡度为衡量混沌蚁群在无线传感网络中演化评判依据，由能量分布程度Bak和路由拓扑均衡度BaL组成，其值越小则路由平衡越好，即网络拓扑长度越短、能量分布越均衡，从而反应无线传感器网络性能越优。

其中：En为第i个节点的能量；Eave是网络所有节点的平均能量，Lm为第m次的网络拓扑路径长度，Lave是生成的所有拓扑路径的平均值。

从而，基于混沌蚁群的自适应路由可以抽象为以下多目标优化问题

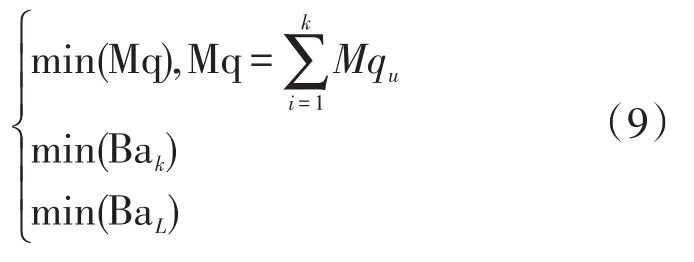
3 算法实现

3.1 混沌蚁群优化模型

本文所涉及自适应路由问题属于离散优化范畴，需要将由Li等人[14]提出的传统CAS模型结合物理学数据场论在多维度进行扩展，从而构造一种离散形式的CAS算法模型。在混沌蚁群算法中，蚂蚁i最优位置的更新将受其维值的影响。那么存在一种情况就是当蚂蚁i已经找到全局最优解的维集合时，受其他劣值的影响扰动其适值不理想。同时，由文献[15-16]可知xid的值在搜索过程中极有可能超出变量的搜索范围[-ωd/2,ωd/2]。故可能造成已寻到的全局最优点的维值就会被覆盖且防止蚂蚁进行越围搜索。本文提出搜索范围优化策略，使之减少全局最优点的维值的丢失，并在熵值的基础上加快算法收敛。

同时，假设蚂蚁i的邻域内有h只蚂蚁，其邻域熵Gi为

式（10）表示第t步蚂蚁i在其邻域内的自组织能力的程度。根据文献[17-19]，当负熵流大于正熵流时，该群体将产生自组织功能。即Gi(t)值越小，该蚁群的自组织能力越强。

通过将蚂蚁的当前迭代自组织变量yi(t)与Gi(t)联合，可以进一步量化蚂蚁的自组织能力，强调了其邻域内个体对蚂蚁i的影响及相互作用，并在自组织能力的控制条件下，蚂蚁个体的混沌行为映射到自组织蚂蚁集合过程的影响。综上，混沌蚁群优化模型如下：

其中：xid(t)为蚂蚁i在第t时刻第d维的位置；为经过越围搜索后的蚂蚁i第t时刻第d维的位置；pid(t-1)为第i只蚂蚁和它的邻居在t-1时刻第d维的最优位置；ψd由第d维参数的搜寻范围确定；vid∈(0,1)决定每只蚂蚁在搜寻范围区域中搜寻不同区域；a为正数，取a=200；b为常数，b∈(0,2/3)。

3.2 邻居的选择

蚂蚁的邻居定义为在搜索空间中距离蚂蚁较近的有限个蚂蚁，其位置因子将影响蚂蚁最优位置的选择。本文从优化网络能耗和网络路由平衡度出发，选择蚂蚁最优邻居，即为延长网络周期的方法之一。在采用上述划分区域方法扇环内节点总势值最高区域为邻居选择区，直至该区域总势值低于其他区域时，才进行下一次的迭代。设定当节点满足其适应值均大于区域节点的适应值时即可当选为蚂蚁的邻居节点。此类选择在保证缩短蚂蚁邻居处于最优的情况下，对网络的能耗及路由拓扑，从而直接延长网络的生命周期。

由混沌蚁群算法性质可知，蚂蚁的邻居个数并非固定不变，而是随蚂蚁混沌行为的演化逐渐呈递增趋势，因此本文设定蚂蚁的邻居数量将随着迭代步数的增加而呈正比关系。

3.3 蚂蚁最优位置更新方法

根据文献[20]，对传统混沌蚁群模型中pid(t-1)-xid(t-1)进行位置信息优化，即使蚂蚁i的第d维的xid向其第d维的最优邻居pid进行移动。pid在数学表达上为蚂蚁i在第t步中的最优位置，即对比t-1步下的蚂蚁i、蚂蚁i的邻居与它们的局部历史最优位置，从中择优。

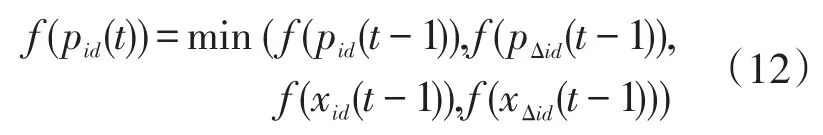
其中：Δi为蚂蚁i的邻居，且与迭代步数呈正比关系；pid(t-1)和pΔid(t-1)分别为蚂蚁i及其邻居Δi在t-1时刻第d维最优位置；xid(t-1)、xΔid(t-1)表示其维值。

3.4 适应值函数

由3.1节可知，基于CAS的自适应路由优化模型的应用背景为多目标优化问题，本文采用线性加权思想，将该类问题主体转化为多个单目标，通过设置网络能耗、能耗均衡度及路由拓扑均衡度三种权重因子，直观的显示数据趋势并取得一种较为平衡的路由优化方案。

其中，α、β和γ为加权因子。

4 仿真实验与结果分析

为证明本文所提出的基于混沌蚁群的自适应路由优化算法(adaptive routing chaotic ant colony，ARCAC）的有效性，选取以下算法进行对比，依次为基于蚁群算法的能量均衡多路径路由算法(ant balance by multipath rouing，ABMR）、基于混沌蚁群的能量均衡路由算法(energy balance chaotic ant colony，EBCAC）、精英蚁群算法(elite ant colony，EAS)和排序的蚁群算法（ant sorted rank，ASrank），主要通过以下三个方面对比这五类算法的性能。

1)平均能量消耗对比率：最优扇环中节点与普通节点的能耗对比值。该值越小表示两类节点能耗越接近，网络整体能量分布越均衡。

2)死亡节点率：为网络中死亡节点数与总节点数的比值。该值越小表示其网络生命周期越长。

3)路由拓扑均衡度：为网络中生成的最终路径的长度均衡度。该值越小表示已生成的最终路径平均长度越短。

4.1 实验环境设置

本文利用Matlab R2012a平台进行仿真，实验参数见表1。

为确定ARCAC算法中的递增蚂蚁邻居个数及维数d的值，根据文献[13]令参照维数d=30，首先分析蚂蚁邻居个数对迭代时间和能量消耗的线性关系，可得出监控区域内最佳蚂蚁邻居个数，接着在此基础上对不同维数d的实验结果进行对比，得出蚂蚁群体最佳维数。

表1 仿真实验参数

4.2 实验结果分析

为分析轮数对本文算法性能的影响，对相同的实验初始条件赋予不同的轮数加以测试，仿真数据验证轮数与网络性能之间的关系。

图2为平均节点能量消耗对比率的对比。平均能量消耗对比率均随轮数的增大而呈总体增大的趋势。ARCAC算法在平均能量消耗对比率上相较于ABMR、EAS和ASrank较低，而略高于EBCAC算法。其中，ABMR算法的能量消耗对比率远大于其他算法，由于该算法单方面结合信息素因子，导致距离Sink节点较近的簇头节点能量大幅度增大从而过早死亡。ARCAC算法不仅考虑了轮数对算法迭代的约束，而且综合考虑了蚂蚁间自主性及节点能量、距离和能耗均衡等因子，构建均衡的适应值及折中的网络性能的网络，从而延长网络生命周期时间。EBCAC算法强调网络的均衡性，以搜索兼顾能耗和最优位置的节点集，但其算法未针对生成路径进行优化策略，导致其平均能量消耗对比率较低。

图2 平均节点能量消耗对比率的对比

图3为死亡节点率的对比。ARCAC算法在死亡节点率上想较于ABMR、EAS、EBCAC算法较低，而略高于ASrank算法。ASrank算法在多次迭代中持续对蚂蚁信息素进行排序，有效的兼顾了多轮条件下网络中的节点情况，所以其节点剩余能量较为均衡，即其死亡节点率较低，但第一个死亡节点时间较早。ARCAC算法在算法初始阶段由于需进行最优扇环与跳转概率的计算，其节点因计算任务所需一定能量，所以死亡节点率在初始阶段偏高，但逐渐趋于平衡。

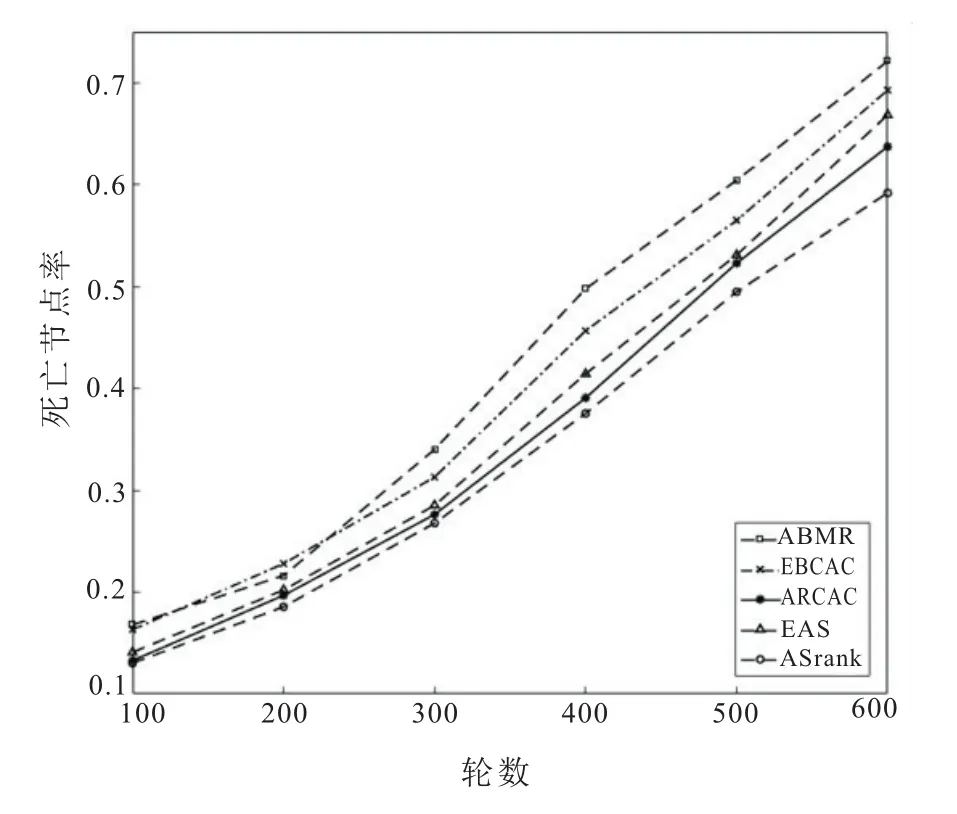
图3 死亡节点率的对比

图4为路由拓扑均衡度的对比。ARCAC算法的路由拓扑均衡度相较于ABMR、EBCAC、EAS和ASrank算法都低且维持稳定状态。ABMR算法忽略了路径的长度与均衡度，故其路由拓扑均衡度较高；EAS算法未考虑节点剩余能量，即网络能耗不均衡，生成的路径之间路径差值较大；ASrank算法过于强调蚂蚁信息素排序而忽略了网络中节点的一般性，多次实验数据对比差异性较大；EBCAC算法虽考虑节点能耗和网络能量均衡等因素，但未对最优节点集为基础生成的路径成都做出相应优化策略。反观ARCAC算法不仅考虑能耗、能量分布程度及路由拓扑长度，从而提升网络性能，延长网络生命周期。

5 小结

本文基于节点位置通过对节点通信区域的划分，同时引入势、熵的概念结合其跳转概论找出扇环区域中适应值较优的节点集，并以混沌蚁群算法为基础对其进行优化，从蚂蚁邻居选择、蚂蚁最优位置更新、等手段寻找全局最优解并构建网络最适应路由拓扑。在不同轮数和不同节点数的条件下，依次与ABMR、EBCAC、EAS和ASrank进行平均能量消耗对比率、死亡节点率和路由拓扑均衡度方面的比较。实验结果表明本算法在需要兼顾能耗和路由拓扑长度的无线传感器网络中能够有效优化路由拓扑长度且有效减少网络能耗，相比于同类混沌蚁群算法与蚁群算法更好的实现了自适应路由，从而延长网络生存周期。

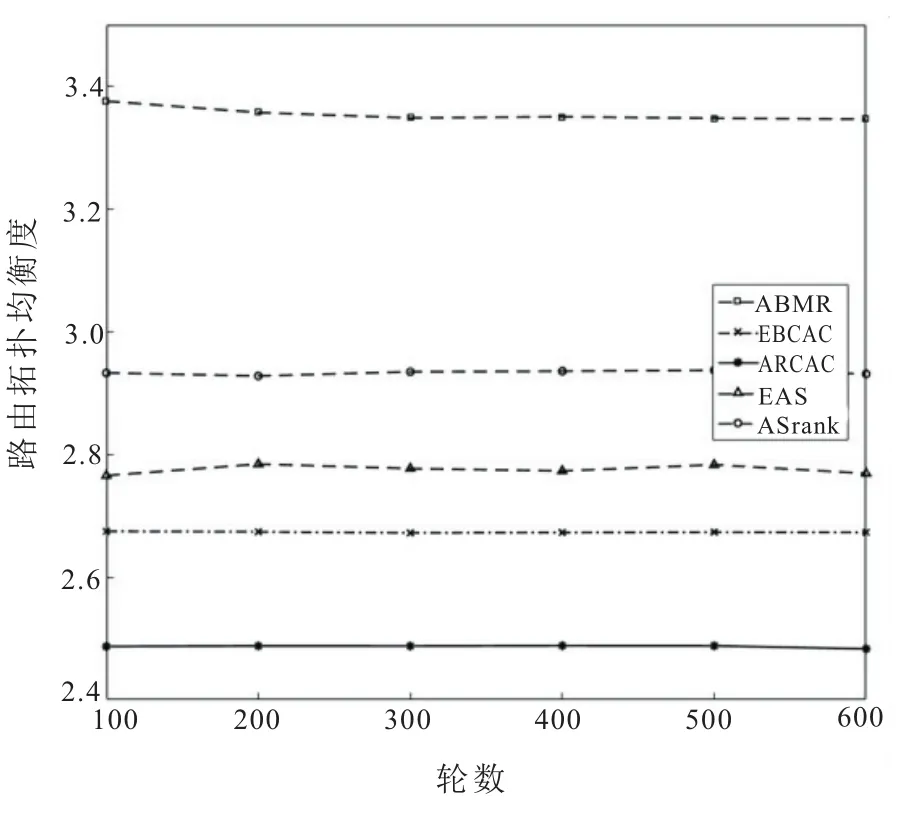
图4 路由拓扑均衡度的对比