薄膜超构表面声扩散体扩散性能研究∗

关淅文 盖晓玲 李贤徽 邢 拓 蔡泽农 王 芳

(北京市劳动保护科学研究所 环境噪声与振动北京市重点实验室 北京 100000)

0 引言

声波在物体表面上的反射很大程度上取决于物体表面结构。施罗德扩散体(Schroeder diffuser,SD)[1-2]的提出，为有序控制声波扩散奠定了重要基础，自此，各种扩散体设计方法被提出用以改进声波扩散方向和适用频带。最经典的施罗德扩散体与随机分布相比，采用了周期结构，通过二次剩余序列设计每一个阱的深度，人为设计声波的反射方向实现声音的漫反射，但施罗德扩散体并没能实现声波尽可能均匀的在所有方向上反射，而且适用的频带较窄。Cox[3-4]等将凹槽之间的隔板去掉，通过迭代算法得到阶梯型扩散体。这种扩散体吸声，且均匀扩散性能较低。D’Antonio等[5-6]运用几何分形理论，通过傅里叶合成和阶梯函数方法调制较小基数结构，设计成幅度格栅扩散体，改善高频扩散性能。Angus[7-8]将扩散体及其反相扩散体按二进制伪随机序列排布推导出调制相位反射格栅扩散体。在此基础上将吸声面和反射面按最大长度序列排布，研究了一维振幅反射格栅扩散体的散射性能，扩散性能提高，但镜面反射增强。RPG公司开发了Binary Amplitude Diffuser[9]，将面板的某些部分按规律弯曲一定角度，使得扩散体扩散方向更均匀。Cox等[10-11]和Xiao等[12]采用三元序列使入射波与反射波在镜面反射方向发生干涉互相抵消，改进了扩散效果，但在偶数倍频程频率处干涉会失效。以上都是对传统施罗德扩散体的改进，共同的缺点在于体积庞大、结构复杂，不利于实用。近年来由于声学超材料的兴起，利用声学超材料构建扩散体能有效降低扩散体尺寸引起了学界的兴趣，文献[13-15]提出了通过激发局域共振在亚波长尺度内产生有限大小的传播相位突变的思路，利用超薄的非经典亥姆霍兹谐振腔构建出厚度仅为SD十分之一的超构表面施罗德扩散体。但结构过于精细，给工程加工带来了很大的不便。薄膜作为常用的声学材料，具有良好的声学性质，一直都用于吸隔声，而薄膜型超材料已被证实具有更优良的声学性质，如Naify等[16]发现其在低频传递损失峰值处有效动态质量密度为负。Mei等[17]设计出在170 Hz能吸收86%入射波的薄膜材料，在某些低频频率处能吸收99%入射波的双层材料等。本文考虑利用薄膜超材料构建声扩散体，利用薄膜的物理特性和超材料的结构特性，在实现声能均匀扩散的同时，确保结构简单，加工方便。

1 数值仿真

本文采用薄膜超材料,将施罗德扩散体的设计方法类比到薄膜超材料上，表面格林函数方程为

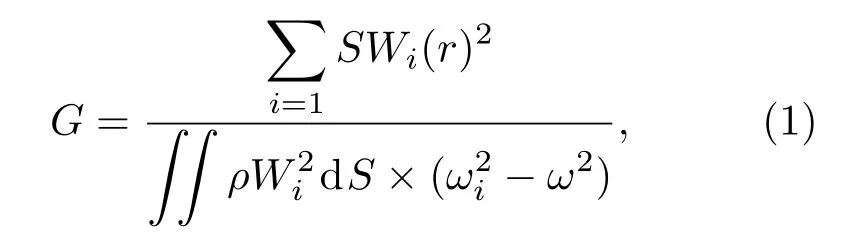
其中，S和ρ分别是表面积和面密度，Wi(r)2和ωi是第i个振动模态和固有频率。薄膜和空腔的阻抗可以表示为表面格林函数的函数，结构胞元总阻抗就是单元阻抗并联之和。图1显示了设计的薄膜超构表面声扩散体结构，通过在四周固支约束的薄膜表面附加金属质量块，以质量块提供额外的约束，限制薄膜的振动，同时薄膜提供给质量块的弹性作用使薄膜超材料减少吸收入射声波能量，并对声能进行各方向的均匀扩散，薄膜上附加张力依次为1 MPa、3 MPa、5 MPa，其本征频率分别为286 Hz、525 Hz、762 Hz。构型框架高度为10 mm，背腔厚度为5 mm，薄膜直径为50 mm，厚度为1 mm，质量块处于薄膜正中央，厚度为1 mm，宽度为4 mm。

图1 模型截面图Fig.1 Model section

利用Comsol Multiphysics建立薄膜超构表面声扩散体的有限元模型，薄膜选用的PET材料密度和声速为ρ1=900 kg/m3，c1=2700 m/s，用于构建声学扩散器的框架的密度和声速分别设定为ρ2=7850 kg/m3和c2=5200 m/s，远大于空气密度ρ0=1.21 kg/m3，c0=343 m/s。在薄膜与框架的连接处，为薄膜施加周向拉力，假设框架结构为刚体材料，不因声波在其上的传播发生形变等，框架的边界条件设置为固定约束，质量块和薄膜之间的连接也采用固定约束。当入射平面波撞击在这种胞元结构的平面阵列上时，通过声扩散体胞元结构表面，互相干涉产生特定的反射场。通过调整作为二次声源的薄膜超材料表面亚波长尺度胞元，有序安排声波的波前。基于此，选择运用PET薄膜并在其表面附加质量块，将其拓展到三维以实现本文提出的声学扩散体的设计。

2 分析与讨论

由声学理论可以得出入射平面波以正入射的方式直接传播到构件上，会引起薄膜附加质量块的震动，通过对张力的调节以及薄膜材料的选择，各个单元结构之间的微小差异得到不同的反射波相位以及不同扩散角度的反射波。以3000 Hz为例，调节薄膜张力，分别附加1 MPa、3 MPa、5 MPa的张力，得到如图2所示的结果，从结果可以看出，随着薄膜张力的增加，扩散声能显著增加，减少了声能转化为扩散体振动产生的内能。当张力由1 MPa增加到5 MPa时，扩散瓣的平均声压级由120 dB增加到135 dB。同时三种张力情况下，扩散体的扩散均匀性保持良好。质量块的大小对扩散体的性能的影响如图3所示，质量块厚度不变，宽度由4 mm增大为6 mm、8 mm会增加扩散声能的耗散，均匀性略微减弱，等效质量的增加使得薄膜超构表面声扩散体的阻尼增加，从而扩散瓣的平均声压级几乎都削减了5 dB。而随着背腔深度增大，扩散声能增加，如图4所示。

图2 薄膜张力变化对扩散性能的影响Fig.2 Effect of film tension change on diffusion performance

图3 质量块大小变化对扩散性能的影响Fig.3 Effect of mass size change on diffusion performance

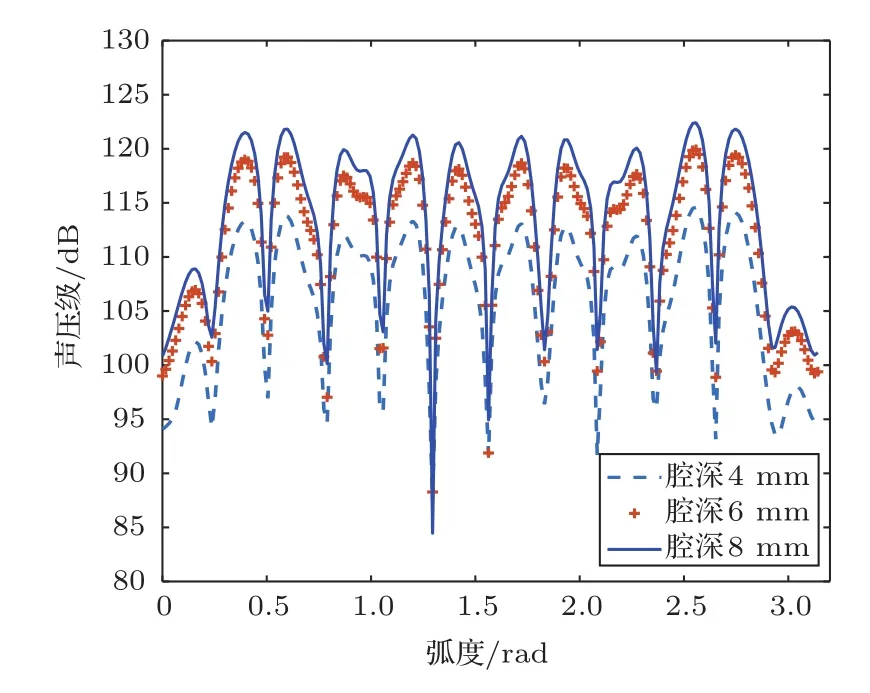
图4 腔深变化对扩散性能的影响Fig.4 Effect of cavity depth variation on diffusion performance

在实际情况中，声学扩散体通常需要用于有限频带的声学信号，并且非常需要宽的工作频带。为了在频率变化时定量评估不同扩散体的性能，采用了一个扩散系数参数，通常用于表征特定频率下扩散的有效性，公式定义如下[18-19]：

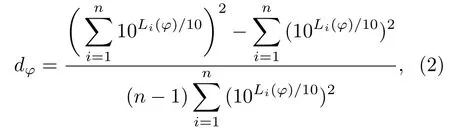
其中，Li(φ)是极性响应中以分贝为单位的声压级，n是接收点数量，下标φ是入射角。通过控制施罗德扩散体和薄膜超构表面声扩散体的尺寸都为87.1 cm×81.7 cm来比较两者之间性能的差异。通过调节薄膜超构表面声扩散体胞元的张力，可以对应用频带进行调节。这些明显优势取决于薄膜超构表面特定胞元结构的构造，根据薄膜超材料的特性，附加质量块的薄膜具有负有效质量和负有效刚度，刚性质量块对声波存在较强的反射作用，薄膜对质量块的牵引，可将复杂系统简化为质量块-弹簧振动模型[16]。受到声波的激励，薄膜牵引质量块运动产生负的有效质量，然后当质量块和薄膜的相位相差180°时，质量块与薄膜运动方向相反，相位差为0°时，质量块与薄膜运动方向相同[20]。附加质量在一定程度上将入射的声波以局域共振的方式衰减，使结构具有了更宽的共振频带。薄膜共振存在黏滞损耗，利用Comsol Multiphysics热声模块，考虑到亚尺度结构整体的黏滞效应，将边界的黏滞效应和薄膜的阻尼的损耗等效设置为薄膜损耗因子，令薄膜损耗因子从0.03～0.1变化，通过仿真结果发现，损耗因子的变化对薄膜型散射体的声能分布没有太大影响。图5给出了损耗因子为0.5和没有黏滞效应的薄膜型扩散体的声能分布。

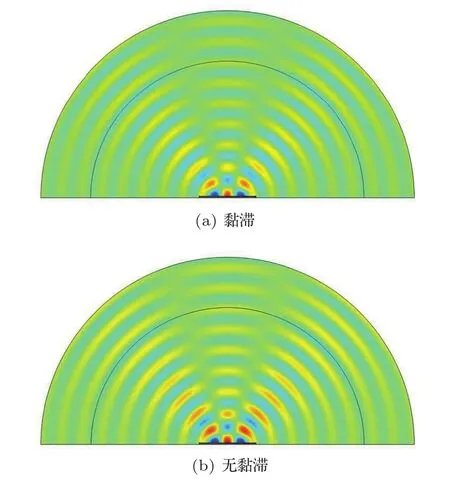
图5 黏滞与无黏滞声场分布图Fig.5 Viscous and non-viscous sound field distribution

现实情况下，声波不可能实现非常完美的垂直正入射，设计声波入射角度为30°、45°、60°得到扩散体的扩散系数如图6所示，对比这三种情况下薄膜超构表面声扩散体和传统施罗德扩散体的性能优劣。其中蓝色和红色两条线表示两种胞元结构厚度分别为10 mm的薄膜超构表面声扩散体和50 mm的施罗德扩散体的扩散系数曲线。通过模拟，可以看出，4000 Hz频带内，三种入射角情况下，薄膜超构表面扩散体的性能都比施罗德扩散体的扩撒性能要好得多。在高频处，由于高阶模态的存在，扩散系数将减小，这表明通过调整结构参数来提高截止频率可以实现薄膜超构扩散体的超宽带宽的可能性。本文提出的扩散器具有简单性和有效性，可为声学扩压器的设计提供一种替代方案。此外，对于需要较大面积的扩散体，可以通过重复排列扩散体胞元结构来构造它。

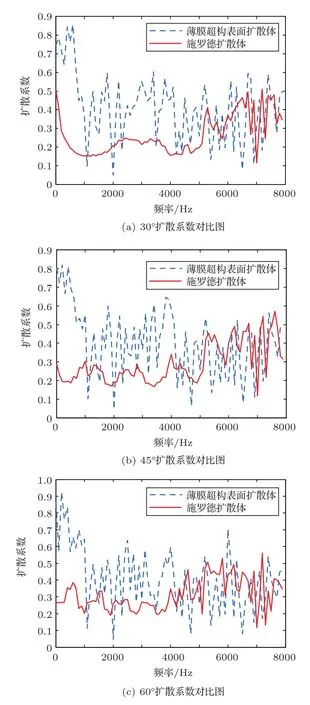
图6 薄膜超构表面扩散体与施罗德扩散体扩散系数对比图Fig.6 Comparison of diffusion coefficient between thin film superstructure surface diffuser and Schroeder diffuser

图7 薄膜声扩散体与施罗德扩散提指向性对比图Fig.7 Contrast of directivity of film acoustic diffuser and Schroder diffusion

在本文设计中，可以通过调制每个单元的反射相位来直接操纵反射声场。通过调节薄膜张力和质量块质量，可以根据实际需要得到特定的反射波。图7给出了相同尺寸的薄膜超构表面声扩散体和施罗德扩散体的指向性对比图，其中每个峰代表不同方向上散射声场的扩散瓣。薄膜超材料的反射声场能直接通过操纵胞元的设计进行调节，从图7扩散瓣的指向性与扩散性可以看出，薄膜超构表面声扩散体相较于施罗德扩散体而言，在图示的五个特定频率内，扩散瓣更多且声能分布更均匀。

3 结论

综上所述，本文基于超材料的波前处理的概念，提出了一种薄膜超材料扩散体，它能够通过直接操纵反射波的波前，以更易操作和更均匀的方式扩散声能，形成更均匀的期望波场。通过与商业化施罗德扩散体之间比较的数值结果证明，薄膜超构表面扩散体优于施罗德扩散体，在更宽的频带内能产生更均匀的反射波。黏度的影响可以忽略不计，因为边界层厚度远小于元件的宽度。因此，可以通过调整单个元件的尺寸来进一步扩大带宽，这是本文设计的另一个独特优点。设计简单，性能更优，本文提出的扩散器更有望在工程应用上提供一条途径。