承前启后 深耕本原
——由“直线与圆的位置关系”引发的思考
□刘清清 卫德彬
(肥西县上派初级中学,安徽肥西 231200)
一、考试分析引发的调研
问题 如图1,在Rt△ABC中,已知∠C=90°,∠BAC的角平分线AD交BC边于点D.以AB边上一点O为圆心,过A,D两点作圆O(不写作法,保留作图痕迹),再判断直线BC与圆O的位置关系,并说明理由.
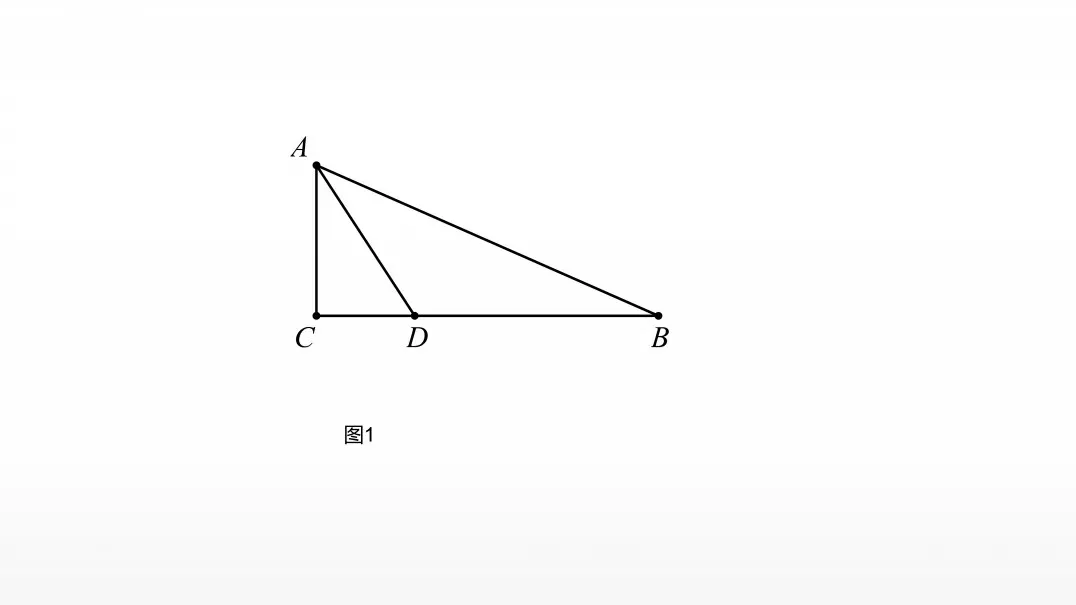
图1
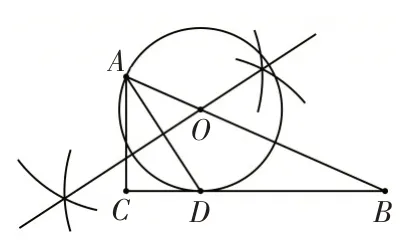
图2
以上问题是2019年肥西县教育局组织的九年级第一次质量调研考试中的一道解答题,图2 是该问题的尺规作图.第一问,考查的知识是“直线与圆的位置关系”.为了了解笔者学校的1150名学生对“直线与圆的位置关系”知识的掌握情况,针对第一问,对全校学生解答情况进行统计.统计结果大致分为三种:①作图正确,判断正确,经过严格推理证明说明判断正确;②作图正确,判断正确,通过观察图2的图象(无证明过程)说明判断正确;③其他.具体统计数据如表1.

表1
由表1 可见,有23.1%的学生采用观察图象完成第一问,而未选择推理证明.为什么会出现这种现象呢?基于疑问,笔者对结果②的266名学生随机抽取11人进行访谈.
教师:为什么会想到这样去解答这道题?
学生a:判断直线与圆的位置关系,有两种方法,一种是利用d与r的关系,一种是利用直线与圆交点的个数.(其他学生附和)
教师:为什么平时“证明直线与圆相切”时,不选择判断交点个数的方法?
学生b、学生c、学生d:因为题目中明确要求“证明”,就必须证明.(其他学生附和)
教师:这一题为什么没有选择证明?
学生b:因为题目没有明确要求我们证明,只是说“说明理由”,既然从图中可以清晰地看出一个交点,就选择数交点个数.并且用图形解题更快,更节省时间.(其他学生附和)
教师:不怕观察有误吗?或是作图不准,造成观察错误?!
学生b、学生e、学生f:不会.因为直线与圆的位置关系中最有考试价值的只有“相切”!(其余学生附和)
由访谈结果可知,结果②的学生对数学考试的“精准”把握是通过对题目意思以及“数形结合”的理解来实现的.
那么,为什么会出现这种答题心理呢?
二、寻根究底找症结
我国人教版九年级数学教科书对切点的定义是:如果直线与圆只有一个公共点,这时直线与圆的位置关系叫作相切.在教师用书中,本节的教学建议如下:对于直线和圆相切,要向学生指出:这时的公共点是唯一的,有且仅有一个.由直线和圆的三种位置关系,教科书通过一个“思考”栏目,直观得到圆心到直线的距离d与圆的半径r之间的数量关系.这三个结论,通过观察和思考,学生容易得到.应使学生明确,它们既可以作为各种位置关系的判定,也可以作为位置关系的性质.这里,还可以进一步指出:直线和圆的位置关系既可以用它们交点的个数来区分,也可以用圆心到直线的距离和半径的数量关系区分,它们是一致的.接着教师用书给出表2辅以说明.

表2
这段话和表2强调,在分析直线与圆的位置关系时一定要注意数形结合,通过交点的个数也可以判断直线与圆的位置关系.于是,学生“犯错”的原因就浮出水面:①把“判断”当成“说理”.②把“直接观察”的结果当作严格的说理证明.③不理解直线与圆位置关系的本质.那么,直线与圆位置关系的本质是什么呢?教师又该怎样去进行正确的引导呢?
三、追本溯源定教法
判断直线与圆位置关系的代数方法是利用“圆心到直线的距离”与“半径的大小”作比较,即转化为垂线段与半径的大小关系,而垂线段就是圆心与垂足的距离.垂足与圆的位置关系决定着直线与圆的位置关系.综上,判断垂足与圆的位置关系,本质上还是判断点与圆的位置关系.随着学生知识的丰富,在未来的高中教育中,学生就会深晓:相切是极限的一个应用,利用交点个数“决定”是否相切实际上是完全错误的.教师应该适当地利用“超前”的思想(极限思想)来引导学生正确理解相切,而不是从交点个数的角度.否则,就会给学生后续的学习带来影响.
那么,如何让学生已经学习的知识不与后续学习的内容产生认知冲突呢?笔者认为应该在课堂教学设计上做到既要“承前”,又要“启后”,要抓住核心,深耕知识的本原.教学目标应与学生今后的发展相结合,既要让学生获得知识,又要考虑到学生今后的发展和学习.鉴于此,直线与圆的位置关系这一课题还需要重新架构教学过程.
四、承前启后重架构
基于以上考虑,笔者提倡一种承前启后、深耕本原的教学思路,具体阐释如下.
(一)温故知新巧导入
首先,以承前式的提问,带领学生进入问题,从新的角度认识直线与圆的位置关系.
教师:我们刚刚学习了点与圆的位置关系,请同学们说一说点与圆的位置关系有几种,又是如何判断的.
学生回答完毕后,教师展示点与圆的位置关系的要点.
教师:若是把点换成直线,直线上的任意一点与圆的位置关系如何呢?(多媒体展示点换成直线,并呈现圆与直线相离的情况)
学生1:都在圆外.
教师:具体说一说.
学生2:直接观察得到.
学生3:在直线上任意找一点记为A,连接AO,因为AO>r,所以直线上的点在圆外.
教师:像这种直线与圆的位置关系我们叫作“直线与圆相离”.同学们,今后判断直线与圆是否相离,有没有更简捷的方法呢?
学生代表:找到离圆心最近的点,判断该点与圆的位置关系即可.过圆心作直线的垂线,因为垂线段最短,所以垂足就是离圆心最近的点.因为垂线段大于半径,则垂足在圆外,所以直线与圆相离.
教师继续拉动直线,直至直线与圆相交.
教师:这时,直线上的任意一点与圆的位置关系又如何?
学生4:有些点在圆外,有两个点在圆上,还有一些点在圆内.
教师:像这种位置关系我们称之为相交.请同学们思考,有没有类似于判断直线与圆相离的方法,简捷地判断相交呢?
学生5:还是找离圆心最近的点,也就是找垂足.垂线段小于半径,垂足在圆内,则直线与圆相交.
【设计意图】教学无论是何种形式,教学的初心是为了让学生更好地理解与认识新知,并为继续学习做好铺垫.承前启后的教学方式正是体现了这一宗旨.以前一节知识作为引入,通过点与直线的位置关系过渡到认识直线与圆的位置关系,这样的引入更为顺其自然,知识的逻辑关系更为流畅.
(二)极限思想来相助
在基础性知识学习的前提下,教师通过讲解、阐述、提问,带领学生更深入地进入问题的本质.
教师:这两个交点我们记为点A,B,现在点A固定不动,让直线绕着A点逆时针(或顺时针)旋转,请同学们仔细观看,说说你看到了什么.(见图3)
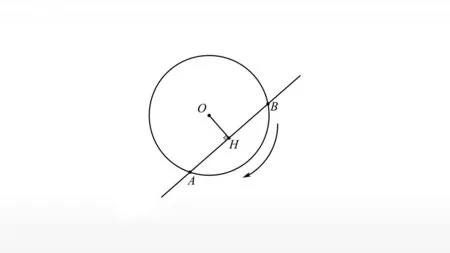
图3
学生6:点B沿着圆周慢慢地向点A滑动,并与点A重合,垂足H也与点A重合.
学生7:当点B越来越靠近A时,无论是逆时针还是顺时针旋转,直线的位置是确定的.
教师:像这样,直线与圆的位置关系称之为相切,唯一的公共点叫作切点,这条直线叫作切线.从上面的操作可以看到,切点是直线与圆相交步步夹逼出现的极限情形,我们将在高中学习极限.那么,我们还可以用类似于前面的办法判断直线与圆是相切的吗?
学生8:可以.当垂足在圆上时,直线与圆就是相切的.
【设计意图】直线与圆相切是初中生初尝极限思想的案例之一,几何画板动态地演示极限的思想,交点、切点、垂足的“三点合为点A”,于是引出相切.利用极限思想让学生体会直线与圆相切时垂足就是切点,而垂足只有一个,所以直线与圆相切时只有一个公共点.这才是直线与圆相切的本质所在.如此就避免了学生对相切理解的偏差,或是只局限于公共点个数上.
教师:由此我们可以看到,判断直线与圆的三种位置关系可以转化为判断什么?
学生9:判断垂足与圆的位置关系.若垂足在圆外,则直线与圆相离;若垂足在圆上,直线与圆相切;若垂足在圆内,则直线与圆相交.
学生10:判断垂线段与半径的关系.
学生11:判断圆心到直线的距离与半径的关系.
教师:直线与圆位置关系的判定也可以转化为判断垂足在何处!与我们上一节学习的点与圆的位置关系一脉相承.从“数”的角度来看,即是判断圆心到直线的距离与半径的关系.
【设计意图】深耕知识的本质,需要我们统观数学,思考知识的内在关联,关注旧知、新知、未学知识三者的相互衔接.回到本节课,判断直线与圆的位置关系(新知)就是判断垂足(点)与圆的位置关系(旧知),而相切就是极限情形(未学知识).这样才关注了直线与圆的位置关系的本质,关注了新知与旧知的密切联系,关注了前面知识对后续学习的横向迁移作用.此时,学生对表2的理解是质的飞跃,而非停留在表面.
2013 年,章建跃在《构建逻辑连贯的学习过程使学生学会思考》[1]中提到学生的学习应该是“前后一致、逻辑连贯的学习过程”.此文警示我们教学时不能只顾着“一亩三分地”,要思考知识的前后关联,更好地让学生构建知识体系.教师如果在备课中做到“前后一致、逻辑连贯”,体现知识的承前启后,于生于师都是大有裨益的.如此双赢,我们为什么不去尝试呢?

