基于地铁历史数据的PCA-RF分时段客流预测方法

马延龙，杜晓华，李明臻

（1. 盘缠科技股份有限公司，北京 100081；2. 北京邮电大学 网络与交换国家重点实验室，北京 100876）

0 引言

随着现代交通的发展，越来越多的人选择乘坐地铁出行，客流预测无疑是轨道交通运营和维护中一个重要的环节，客流预测可以给轨道交通管理部门提供制定实时运营计划的依据[1]，例如：客流预测可以决定列车编组、行车密度和行车线路，还可以帮助拟定票价政策，售检票制度、形式和规模[2]。同时，客流预测还可以给乘客的出行安排提供参考，因而具有十分重要的意义和研究价值。

目前，越来越多的学者将统计学方法用于交通客流预测中。谢海红等[3]对K近邻算法进行了改进，用模式距离搜索算法代替原有的欧氏距离搜索方法，同时引入多元统计回归模型，并将其用于短时交通流预测，在提高搜索效率的同时准确地刻画了交通流的真实情况。但是该算法只是考虑了向量的起伏状态，没有考虑如重大节日等外部因素对交通流的影响，且不具备长期稳定性，需要不定期更新回归数据样本，会产生很大的计算量。雷定猷等[4]提出一种基于非线性主成分分析和GA-RBF神经网络（NPCA-GA-RBF）的高速公路交通量预测方法，进一步提高了交通量预测精度，减少了交通量预测复杂度，但是该算法同样没有考虑其他因素对交通流量的影响。何九冉等[5]充分考虑到城市轨道交通客流变化的线性及非线性特征，将ARIMA模型和RBF神经网络组合，建立了ARIMA-RBF预测模型，并用该模型对北京市城市轨道交通平常日客流量进行预测，取得了较好的预测效果，但是算法增加了模型的复杂度，ARIMA和RBF算法必须串行执行，增加了运算时间。

因此，考虑到随机森林算法（RF）速度快、抗噪能力强等特点，提出使用RF回归构建预测模型，采用历史数据并综合考虑站点地域和节假日等因素[6]，预测地铁站点分时段客流的方法。

1 PCA-RF模型设计

R F具有高度灵活性，以集成学习算法Bagging的思想为基础，有着很强的抗噪能力且易于并行化，具有广泛的应用前景，常用来解决分类、回归和特征选择等问题[7-8]。使用主成分分析法（PCA）[9]和RF来构建客流预测模型（PCA-RF），该模型基于地铁的历史客流数据进行回归分析，通过历史数据预测未来各站点在一段时间内的客流量。

1.1 PCA-RF模型建立流程

客流预测模型的建立，首先要对得到的数据集进行预处理和特征提取；然后以小时为单位，从影响地铁某站点在该时段客流量的众多因素中选取多个影响因素作为训练特征，构成特征向量，得到训练集和测试集；最后用RF对训练集进行训练得到PCA-RF模型。PCA-RF模型建立流程见图1。

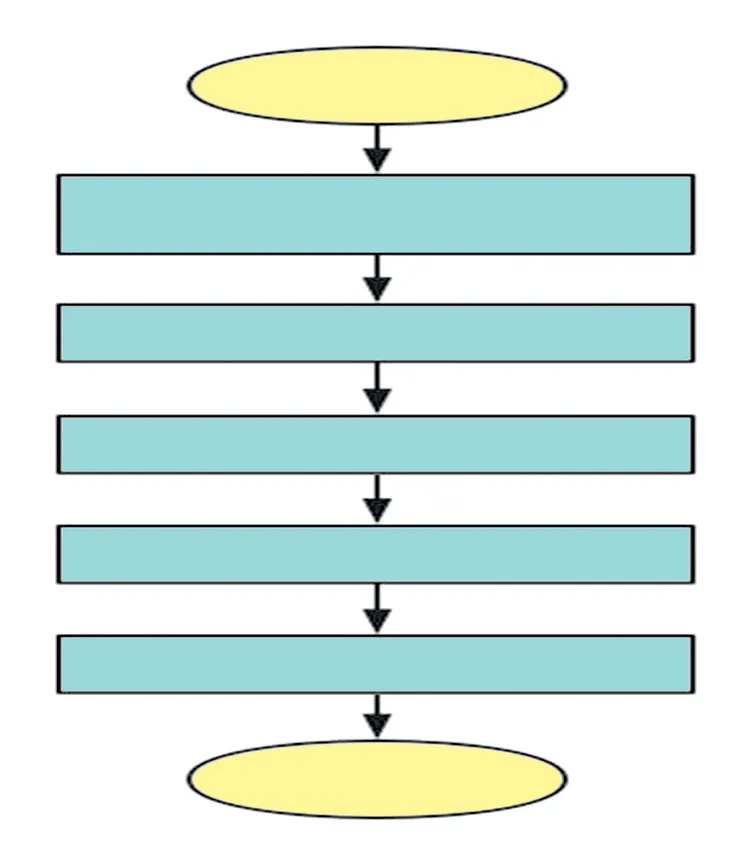
图1 PCA-RF模型建立流程

1.2 具体流程说明

1.2.1 选取数据集和数据清洗

首先选择契合客流预测分析的数据集；随后的数据清洗能够有效地提升数据的质量，主要包括填补缺失值、去掉或更正明显错误的值等，如需将地铁每日停运时段的客流值置为0。

1.2.2 特征提取与数据标准化

以小时为单位划分时段，以地铁某站点在各个时段内的客流量作为预测目标，提取多个与之密切相关的影响因素构成特征向量。主要从时间和空间2个维度来提取数据特征。时间特征包括日期、节假日、高/平峰时段[6]、时间段。为了方便进行数学运算，特征日期统一转化为时间戳的数字形式；对于节假日，分别使用数字0代表工作日、1代表双休日、2代表国家规定放假的特殊节日（如国庆节和中秋节等）；对于高/平峰时段，定义每日6：00—9：00和16：00—20：00为高峰时段，用数字1表示，其余时间为平峰时间段，用0表示；对于时间段，每日0：00—6：00为地铁停运时段，用0表示，其余时段以小时为单位划分，分别用数字表示，例如8：00—9：00为1个时段，用数字8表示。考虑到城市地铁站的地域分布对客流的影响，以该城市地铁线路图建立平面直角坐标系，将其等分为16块区域，每个区域对应1个X坐标和1个Y坐标，然后将每个站点映射到各个区域中。基于此，空间特征包括站点线路，是否换乘站，站点所属区域在平面直角坐标系的X坐标、Y坐标。站点线路用其自身的线路编码表示；换乘站和非换乘站分别用数字1和0表示；站点的X坐标和Y坐标分别编号为数字0—3。另外，机场或火车站等客运交通枢纽和普通站点的客流分布有着显著不同，所以另外附加1个特征——是否客运交通枢纽（用于和普通站点进行区别）。最终提取得出的客流特征见表1。

将处理过的原始数据映射到这些特征中，得到由一系列特征向量构成的新数据集D。由于RF可以直接使用袋外（OOB，由于RF独特的工作模式，存在一部分样本没有被选中用于模型训练，这部分样本称为OOB样本）数据作为验证集进行参数调优，无需额外构造验证集，所以只需将数据集D划分为训练集和测试集。

表1 客流特征的数据格式

1.2.3 特征指标的权重标注

由于不同的特征对实际客流量的影响程度可能不同，例如在通常情况下，节假日对客流的影响程度显然大于高/平峰时段。故使用PCA对每个特征赋予其各自的权重，使其能够更加全面地反映客流的变化规律，从而提升结果的准确度。

1.2.4 使用RF训练与预测

将加权过后的训练集输入到RF中进行训练和参数调优。在进行参数调优时，可以直接使用OOB样本作为验证集进行参数调优，无需额外选择数据作为验证集。RF的主要参数见表2。

如果数据量很大，为了提升调优效率，则可以使用网格搜索综合坐标下降的调优方法进行参数调优[10]。通过网格搜索遍历规定的所有参数组合，通过交叉验证得到最优参数。坐标下降其实是一种贪心算法，选取对模型结果影响最大的参数先进行调优，再选取影响程度次大的参数调优，如此循环，直到得到所有需要的参数，但是坐标下降最终只能得到局部最优的结果。

模型训练结束后，使用测试集进行测试，最后评价模型的预测结果。

2 PCA-RF模型实例

2.1 数据来源与预处理

选取广州地铁某单程票售票APP中的出票数据进行模型构建，其中客流概念定义为一段时间内某一站点的进站客流量。选取广州地铁该售票APP从2017-05-01—2018-10-03的出票数据，经过特征提取与转化，得到可以用于模型构建的数据1 400 000余条。选取其中1 400 000条数据构成训练集，1 000条数据构成测试集，然后使用PCA法进行特征权重的标注。

表2 RF的主要参数

2.2 模型训练与参数调整

在使用RF时，参数oob_score设定为True，即使用OOB样本评估模型的好坏，criterion选择默认的标准。首先对参数n_estimators进行网格搜索[11]，得到最优的值为130，依次类推，最终得到所有所需的参数值（见表3）。随后使用最优参数和包含1 400 000条数据的训练集对模型进行训练。

2.3 预测与结果分析

模型训练完成后，使用包含1 000条数据的测试集进行回归预测分析，然后对模型的预测结果进行评价。模型预测的前100条测试集样本的结果见图2。

分别使用决定系数（R2）和均方根误差（RMSE）对该预测模型的结果进行评价。

（1）R2：通过数据变化来表征模型拟合的优劣，R2越接近1，表明拟合程度越高。计算公式如下：

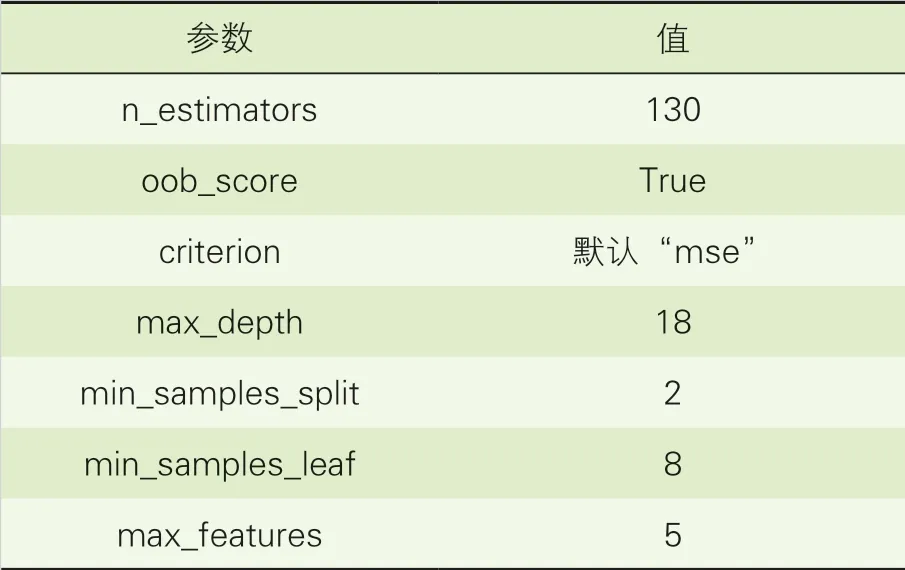
表3 RF调参结果

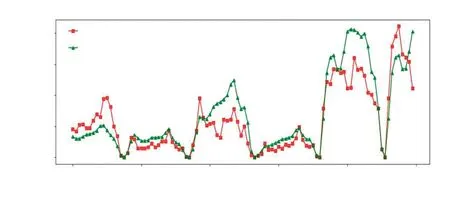
图2 模型预测结果（前100条测试集样本）

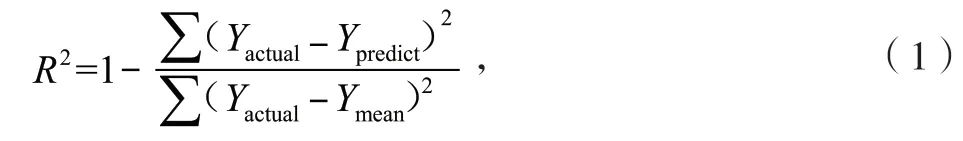
式中：Ypredict和Yactual分别为预测值和实际值；Ymean为真实的均值。

（2）RMSE：用来衡量观测值同真值之间的偏差。n为样本数量，计算公式如下：

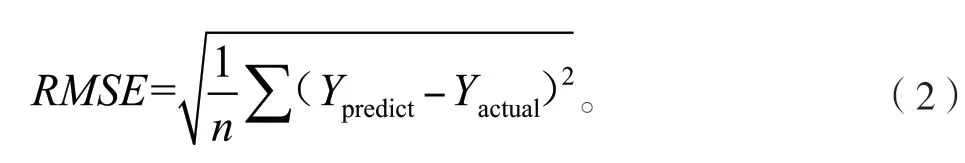
将PCA-RF模型和传统的决策树回归模型（DT）进行比较，分别计算其R2和RMSE值，结果见表4。

可以看出， PCA-RF模型的R2为0.932 7，非常接近1而且远远大于DT模型的0.857 9；RMSE为29.91，也优于传统决策树模型。比较DT模型和PCA-RF模型在前100个样本中的绝对误差，可见PCA-RF模型在绝大多数单独样本上的误差都小于DT模型（见图3）。

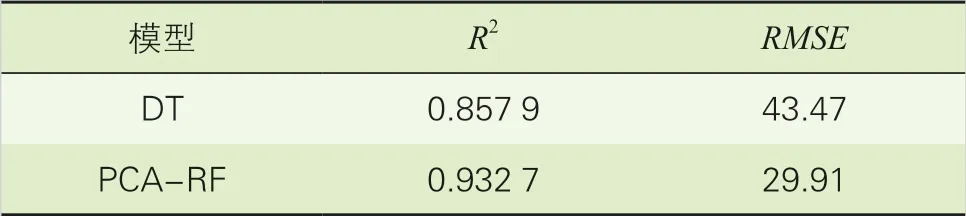
表4 DT模型和PCA-RF模型结果评价

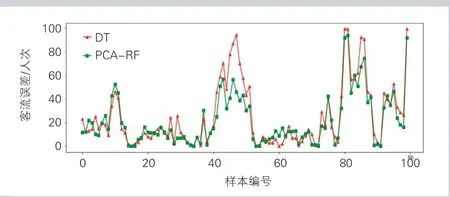
图3 DT模型和PCA-RF模型的绝对误差（前100个样本）

3 结束语

构建了一种基于历史客流数据并使用随机森林算法（RF）的地铁客流预测模型（PCA-RF），经过验证，该模型与实际数据拟合度较高，并且在准确度与稳定性上也优于传统的决策树模型，可为未来相关方面的研究与应用提供思路。