转动惯量存在不确定性的挠性航天器动态自适应滑模姿态控制*

董瑞琦，吴爱国，张 颖，贺 亮

(1. 哈尔滨工业大学 机电工程与自动化学院·深圳·518055；2. 上海航天控制技术研究所·上海·201109)

0 引 言

姿态稳定控制律设计是航天器控制系统设计最重要的一部分，为了满足姿态控制系统设计的高精度、高稳定度的要求[1]，很多控制方法被提出，比如比例微分(Proportion Differentiation，PD)控制算法[2]、滑模控制方法[3]以及自适应律[4]。

滑模控制律(Sliding Mode Control, SMC)是一种非线性控制策略，由于它自身的强鲁棒性和易实现性，吸引了很多学者的注意。实际上，滑模控制律还具有对于模型匹配不确定性以及外部干扰的不敏感性[5]等优点。因此，滑模控制律被广泛应用于航天器姿态控制律设计中。在文献[6]中，通过解一个简化模型的最优控制问题，提出了滑模控制律。该文基于姿态角速度和姿态角信息构造了最优的切换面。为了进一步提高到达滑模面过程中系统状态的瞬态响应，文献[7]提出了光滑的模型参考滑模控制律。在文献[8]中，滑模控制律用于解决航天器的姿态跟踪问题。为了处理滑模控制律的抖振问题，文献[9]针对刚体航天器设计了高阶滑模控制律。文献[10]针对挠性航天器设计滑模姿态控制律。

前述的滑模控制律包含两个部分：由被控系统的名义部分推导得到的等效控制，以及处理系统的不确定性和外部干扰的控制项。并且上述文献中提出的算法在设计滑模控制律过程中，要求由系统不确定性和外部干扰构成的函数的上界可以得到。然而，在实际应用中，这个函数的上界很难得到。因此，解决该问题非常保守的办法就是选择一个非常大的切换增益，以保证设计的控制律对于系统的不确定和干扰有足够的鲁棒性。然而，非常大的控制增益会激发抖振，甚至导致航天器姿态系统失稳[11]。目前，有两种主要的策略可以解决不确定性和干扰上界未知的问题。一种方法是利用文献[12]描述的干扰观测器方法，利用该方法设计控制律时，通常假设干扰和模型的不确定性由线性外源性系统引发[13]。由于参数不确定性和干扰很难预测，因此该条件在实际应用中很难满足。另一种方法是利用参数自适应策略。通过假设不确定性上界与系统状态线性相关，文献[14]提出了两种自适应滑模控制律。但是，该文献中构造的滑模函数是非连续的，不连续的滑模函数可以引起抖振。为了减弱抖振问题，文献[15]对滑模面设计了一个边界层，并且提出基于改进自适应律的滑模控制律。此外，自适应滑模控制方法被用于处理不确定挠性航天器的鲁棒姿态控制问题[16]。

上述提到的研究都是针对刚体航天器设计姿态控制律。然而，现代航天器携带大型的、复杂的轻质材料，比如太阳能电池板、天线等，因此现代航天器都是挠性的。航天器的这些挠性结构通常会有低频的振动模态[1]。这些振动模态可能会导致一系列问题包括姿态控制精度，甚至会导致系统失稳。此外，当航天器在轨运行时，材料消耗、挠性附件的伸展和收缩都可能会影响系统的转动惯量。因此，挠性航天器姿态控制系统设计必须要考虑转动惯量不确定性。

本文是会议论文[17]的修改提高版本。本文内容安排如下：首先，简单介绍挠性航天器系统;其次，利用可获得的姿态信息构造了部分状态观测器估计挠性航天器的挠性模态；再次，利用姿态信息设计滑模面，并且设计自适应律估计由不确定性和外部干扰组成的函数的上界；最后，利用Lyapunov稳定理论设计了可以镇定闭环航天器姿态控制系统的自适应滑模姿态控制律。此外，采用本文设计的控制律和现有方法对一个挠性航天器进行对比试验。

1 数学模型的建立

1.1 数学模型

本文采用单位四元数描述挠性航天器的姿态，得到如下航天器姿态运动学方程：

(1)

式中：q0和qv=[q1q2q3]T∈R3分别为单位四元数q的标量部分和向量部分；ω=[ω1ω2ω3]T∈R3为航天器本体角速度；T(q0,qv)为

(2)

其中，I3为3×3的单位矩阵，对于任意的向量x=[x1x2x3]T∈R3，x×的定义为：

(3)

显然，对于任意的三维向量x，x×是一个反对称矩阵。并且，单位四元数满足如下的约束：

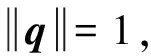
(4)

假设挠性附件的弹性形变很小[18]，利用欧拉定理，得到如下挠性航天器的姿态动力学方程[19]：

(5)

式中：Jmb为挠性航天器刚体部分的转动惯量；Φ∈R3×4为挠性附件与航天器主体之间的耦合矩阵，用以描述挠性附件对航天器本体的影响；η为挠性附件的位移向量；ψ为中间变量；u为作用在航天器主体上面的外部输入力矩；d为作用在航天器上的外部干扰力矩；C,K分别为挠性航天器的阻尼矩阵和刚性矩阵。针对本模型，考虑N阶挠性模态，并且C,K为：

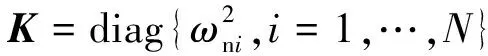
(6)

其中，ωni,i=1,2，…,N和ζi,i=1,2，…,N分别为自然频率和阻尼系数。

注1：本文将文献[20]中刚体航天器的结果推广至挠性航天器。类似地，针对挠性航天器系统(5)，为了避免矩阵T(q0,qv)在q0=0时发生奇异，本文中对挠性航天器的工作区间给出如下约束：

(7)

下面引理给出矩阵T(q0,qv)的性质。

引理1[19]：针对矩阵T(q0,qv)，有下述关系式成立：

(8)

式中：x=[x1x2x3]T∈R3为任意一个三维列向量。

1.2 问题描述

2 主要结果

本节首先构造部分状态观测器估计不可测的挠性模态(η,ψ)。然后，基于姿态四元数q和姿态角速度ω设计滑模函数。其次，为了估计转动惯量不确定性和外部干扰组成的函数的上界，提出自适应律。最后，推导带有转动惯量不确定性和外部干扰的挠性航天器的动态自适应滑模姿态稳定控制律。

2.1 挠性模态观测器

为了估计不可测的挠性模态，构造下述挠性模态观测器，

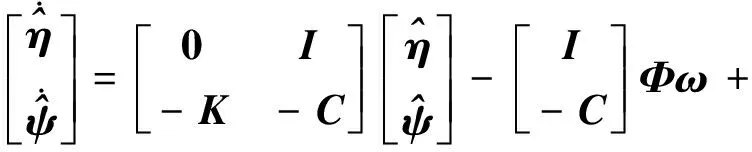
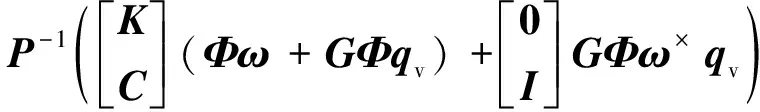
(9)

式中：矩阵P为下述Lyapunov方程的解

其中，矩阵Q满足Q=QT>0。

利用构造的挠性模态观测器(9)可以得到挠性模态位移的估计，利用估计得到的挠性模态信息，接下来设计挠性航天器(5)的动态自适应滑模姿态稳定控制律。

2.2 基于部分状态观测器的自适应滑模控制律

针对挠性航天器(5)，假设姿态四元数q和姿态角速度ω可测，我们将要设计动态自适应滑模姿态稳定控制律。首先，构造如下的滑模函数：

s=ω+Gqv

(10)

式中：G为3×3的对称正定常数矩阵。接下来，通过下述定理给出构造的滑模函数的有效性，即证明姿态四元数q和姿态角速度ω在滑模面s=0上可以滑动至0。

定理1针对带有转动惯量不确定性和外部干扰的挠性航天器系统(5)，当系统的姿态四元数q和姿态角速度ω限制在滑模面s=0上时，系统的状态最终趋于0。

证明：首先，选择下述的Lyapunov函数：

(11)

利用条件s=0，以及引理1，可得

(12)

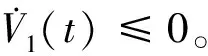
定理1证毕。

基于上述构造的滑模面，下面将要设计挠性航天器的动态自适应滑模控制律。考虑下述形式的状态反馈控制律：

u=ueq+ud+uh

(13)

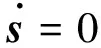
(14)

通过挠性航天器系统(5)的第二个方程可得名义系统如下：

ΦT(Cψ+Kη-CΦω)+u]

(15)

将上述表达式和系统(5)的第一个方程代入(14)，可得ueq

ueq=ω×(Jmb0ω+ΦTψ)-ΦT(Cψ+Kη-

(16)

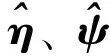
(17)

为了设计控制项ud，首先给出函数ϑ的定义如下，

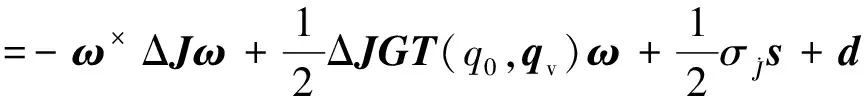
(18)

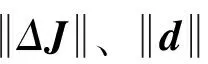
(19)

式中：函数ρ(t,ω)仅与姿态变量ω有关，而与ΔJ、d无关。

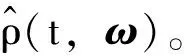
假设1：假设存在正数c0、c1使得下述等式成立：

(20)

基于上述假设，设计控制项ud如下：

(21)

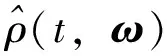
(22)

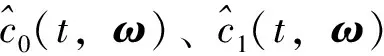
最后，设计控制项uh如下：

uh=-Ws-DF(s)

(23)

式中：W、D均为正定对角矩阵，矩阵F为

(24)

总结前述推导，可以得到下述基于部分状态观测器动态自适应滑模控制律，

(25)

接下来，通过下述定理验证所设计的基于部分状态观测器的动态自适应滑模控制律的有效性。

定理2针对存在未知上界的转动惯量不确定性和外部干扰的挠性航天器系统(5)，首先定义下述挠性模态观测误差：

(26)

采用动态自适应滑模姿态稳定控制律(25)，挠性模态的观测误差eη、eψ以及切换函数s最终趋于0。

证明：选择如下的Lyapunov函数：

V2(t)=V3(t)+V4(t)

式中：

(27)

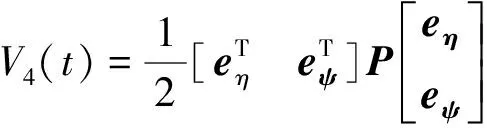
(28)

对(27)和(28)分别求导可得：

(29)

(30)

将式(5)中的第一个等式和第二个等式代入(29)中可得，

(31)

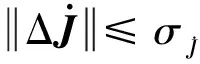
(32)

根据式(18)和(26)可得：

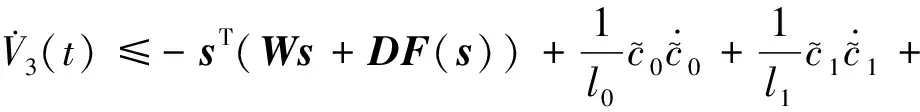
ΦTKeη)+sT(ϑ+ud)

(33)

通过利用式(21)可得，

(34)

利用式(20)和(22)，可得，

(35)

结合式(22)，可得，

(36)

对式(28)求导，并结合式(9)可得，

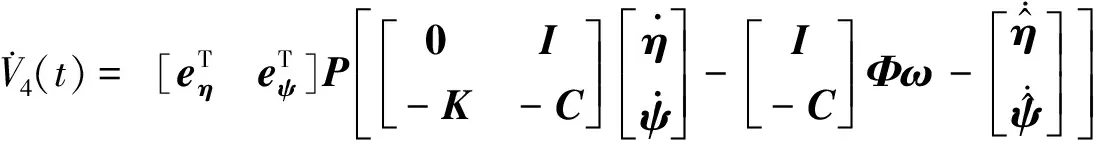
(37)

结合式(36)和(37)可得，

(38)

这表明，滑模函数最终趋于滑模面s=0，并且挠性模态的观测误差eη、eψ最终趋于0。证毕。

本文中提出的动态自适应滑模控制律适用于存在转动惯量不确定性和外部干扰的航天器挠性模态不可测时的姿态稳定控制问题，并且该控制律不需要已知转动惯量不确定性和外部干扰的上界。

3 仿真分析

为了验证控制器(25)的有效性，参考文献的仿真算例，将航天器各参数选取如下：

挠性航天器的名义转动惯量的标称值Jmb(kg·m2)为：

挠性附件与刚体之间的耦合矩阵Φ(kg1/2·m)为：

此外，考虑前四阶挠性附件的振动频率为：

ωn1=0.7681rad/s,ωn2=1.1038rad/s
ωn3=1.8733rad/s,ωn4=2.5496rad/s

和前四阶挠性附件的振动阻尼为：

ζ1=0.005607,ζ2=0.00862
ζ3=0.01283,ζ4=0.02516

姿态四元数的初始值为：

q0(0)=0.173648

在仿真中，角速度的初始值设为：

挠性航天器挠性模态变量的初始值为：

ηi=0.001,ψi=0.001,i=1,2,3,4

外界干扰信号d为：

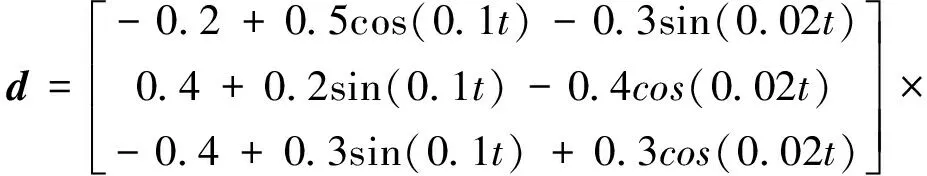
10-3(N·m)

控制器的可调参数选取为

G=diag{0.5,0.5,0.5},l0=5,l1=5
W=20I3×3,D=5I3×3,Q=2I3×3

考虑挠性航天器的旋转角度为160°，欧拉轴为：

机动目标为：在40s内使挠性航天器从初始状态机动到目标状态，并且有效地抑制振动。

与文献[21]中定理2提出的控制律(在本文中称为Controller A)对比的仿真结果在图1中。其中，实线代表本文提出的动态自适应滑模姿态稳定控制律(Dynamical Adaptive Sliding Mode Control, DASMC)，蓝色虚线代表文献[21]中提出的Controller A。

通过总结仿真结果可得，本文提出的动态自适应滑模控制律不会产生抖振，并且在有限时间内可以镇定挠性航天器系统。

(a)挠性模态位移响应

(b)控制力矩响应曲线

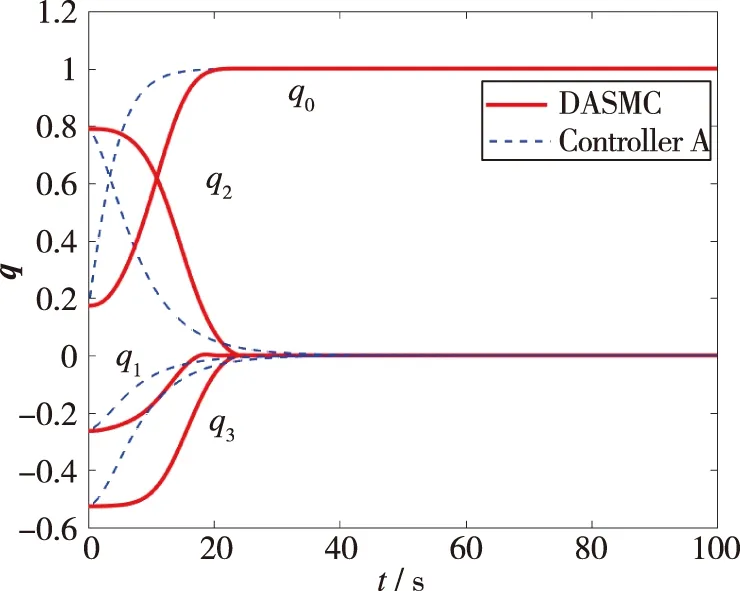
(c)姿态四元数响应

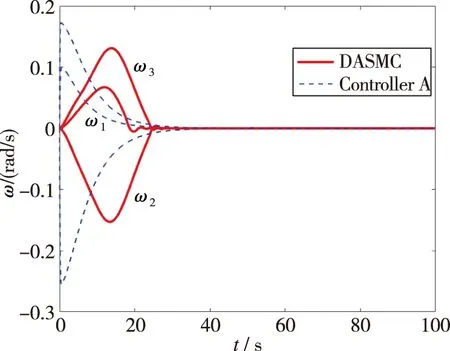
(d)姿态角速度响应图1 DASMC控制律与 Controller A比较Fig.1 Comparison of DASMC law and controller A

4 结 论

本文主要研究了存在转动惯量不确定性和外部干扰的挠性航天器的姿态稳定控制问题，并设计基于观测器的动态自适应滑模姿态稳定控制律。

本文设计的控制律不需要转动惯量不确定性以及外部干扰的先验知识，并且还适用于挠性模态不可测的情况。利用李雅普诺夫稳定性理论分析了挠性航天器闭环系统的稳定性。另外，通过将所设计的控制律运用于四阶挠性模态挠性航天器系统中，验证了系统状态的收敛性。