2019年高考数学模拟试卷(四)
2019-12-02 05:22本刊编辑部试题研究中心
中学生数理化·高三版 2019年8期
本刊编辑部试题研究中心
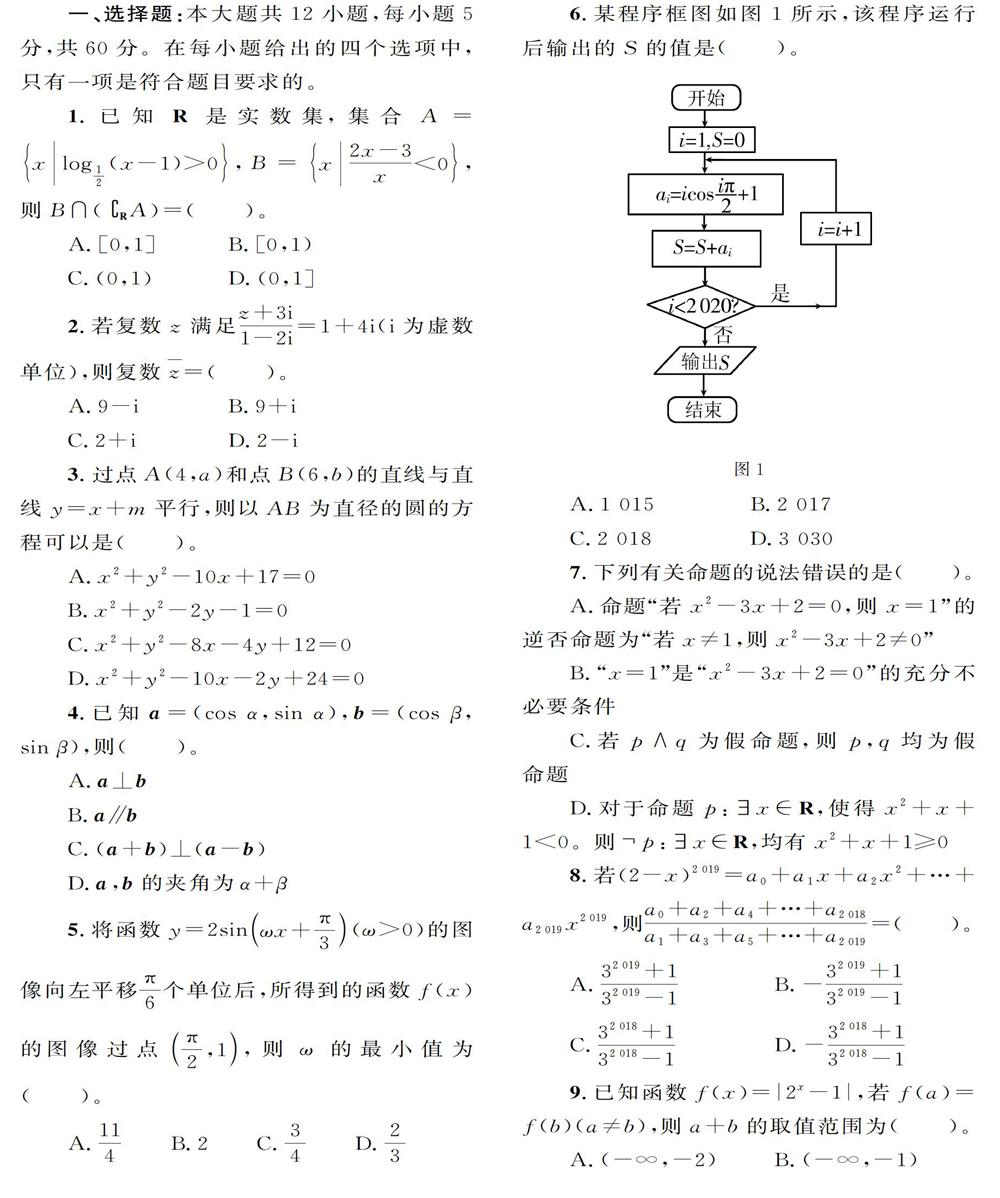


一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
18.(本小题满分12分)
某社区为了丰富居民节日活动,组织了“迎新春”象棋大赛,已知由1,2,3号三位男性选手和4,5号两位女性选手组成混合组参赛。已知象棋大赛共有三轮,设三位男性选手在一至三轮胜出的概率依次是5/6,3/5,2/3;两位女性选手在一至三轮胜出的概率依次是3/4、2/3、1/2。
(1)若该组五名选手与另一组选手进行小组淘汰赛,每名选手只比赛一局,共五局比赛,求该组两名女性选手的比赛次序恰好不相邻的概率;
(2)若一位男性选手因身体不适退出比赛,剩余四人参加个人比赛,比赛结果相互不影响,设X表示该组选手在四轮中胜出的人数,求随机变量X的分布列和数学期望。
19.(本小题满分12分)
如图3,半圆o的直径AB长为4,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,
分析:(1)先化简再利用正弦函数的单渊性得出减区间。
(2)先直接根据平移和伸缩变换得到g(x)的提示式,再根据正弦函数的值域求得结论。
(责任編辑 王福华)
猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
孩子(2021年1期)2021-01-27
中学课程辅导·高考版(2019年8期)2019-07-31
中学课程辅导·高考版(2019年8期)2019-07-31
理科考试研究·高中(2017年7期)2017-11-04
数学学习与研究(2016年19期)2016-11-22
小学生导刊(低年级)(2016年9期)2016-10-13
中学生数理化·高二版(2016年9期)2016-05-14
学苑创造·B版(2015年11期)2016-01-13
数学教学通讯·初中版(2014年1期)2014-02-14

